diff --git a/机器学习/殷康龙/机器学习笔记/3.决策树.md b/机器学习/殷康龙/机器学习笔记/3.决策树.md
index 23e9c771..404c5f18 100644
--- a/机器学习/殷康龙/机器学习笔记/3.决策树.md
+++ b/机器学习/殷康龙/机器学习笔记/3.决策树.md
@@ -1,8 +1,7 @@
-
# 第3章 决策树
-## 决策树 概述
+## 1 决策树 概述
`决策树(Decision Tree)算法是一种基本的分类与回归方法,是最经常使用的数据挖掘算法之一。我们这章节只讨论用于分类的决策树。`
@@ -10,11 +9,11 @@
`决策树学习通常包括 3 个步骤: 特征选择、决策树的生成和决策树的修剪。`
-## 决策树 场景
+## 2 决策树 场景
-一个叫做 "二十个问题" 的游戏,游戏的规则很简单: 参与游戏的一方在脑海中想某个事物,其他参与者向他提问,只允许提 20 个问题,问题的答案也只能用对或错回答。问问题的人通过推断分解,逐步缩小待猜测事物的范围,最后得到游戏的答案。
+* 一个叫做 "二十个问题" 的游戏,游戏的规则很简单: 参与游戏的一方在脑海中想某个事物,其他参与者向他提问,只允许提 20 个问题,问题的答案也只能用对或错回答。问问题的人通过推断分解,逐步缩小待猜测事物的范围,最后得到游戏的答案。
-一个邮件分类系统,大致工作流程如下:
+* 一个邮件分类系统,大致工作流程如下:

@@ -24,31 +23,28 @@
如果不包含则将邮件归类到 "无需阅读的垃圾邮件" 。
```
-决策树的定义:
+### 决策树的定义
-分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型: 内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性(features),叶结点表示一个类(labels)。
+* 分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点(node)和有向边(directed edge)组成。结点有两种类型: 内部结点(internal node)和叶结点(leaf node)。内部结点表示一个特征或属性(features),叶结点表示一个类(labels)。
-用决策树对需要测试的实例进行分类: 从根节点开始,对实例的某一特征进行测试,根据测试结果,将实例分配到其子结点;这时,每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配,直至达到叶结点。最后将实例分配到叶结点的类中。
+* 用决策树对需要测试的实例进行分类: 从根节点开始,对实例的某一特征进行测试,根据测试结果,将实例分配到其子结点;这时,每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配,直至达到叶结点。最后将实例分配到叶结点的类中。
-## 决策树 原理
+## 3 决策树 原理
-### 决策树 须知概念
+### 信息熵 & 信息增益
-#### 信息熵 & 信息增益
-
-熵(entropy):
+* 熵(entropy):
熵指的是体系的混乱的程度,在不同的学科中也有引申出的更为具体的定义,是各领域十分重要的参量。
-信息论(information theory)中的熵(香农熵):
+* 信息论(information theory)中的熵(香农熵):
是一种信息的度量方式,表示信息的混乱程度,也就是说: 信息越有序,信息熵越低。例如: 火柴有序放在火柴盒里,熵值很低,相反,熵值很高。
-信息增益(information gain):
+* 信息增益(information gain):
在划分数据集前后信息发生的变化称为信息增益。
### 决策树 工作原理
-如何构造一个决策树?
-我们使用 createBranch() 方法,如下所示:
+* 如何构造一个决策树?我们使用 createBranch() 方法,如下所示:
```
def createBranch():
@@ -85,21 +81,19 @@ def createBranch():
适用数据类型: 数值型和标称型。
```
-## 决策树 项目案例
+## 4 决策树 项目案例
-### 项目案例1: 判定鱼类和非鱼类
+## 4.1 项目案例1: 判定鱼类和非鱼类
-#### 项目概述
+### 项目概述
-根据以下 2 个特征,将动物分成两类: 鱼类和非鱼类。
+* 根据以下 2 个特征,将动物分成两类: 鱼类和非鱼类。特征:
+ 1. 不浮出水面是否可以生存
+ 2. 是否有脚蹼
-特征:
-1. 不浮出水面是否可以生存
-2. 是否有脚蹼
+### 开发流程
-#### 开发流程
-
-[完整代码地址](/src/py2.x/ml/3.DecisionTree/DecisionTree.py):
+[完整代码地址](../源代码/)
```
收集数据: 可以使用任何方法
@@ -336,15 +330,15 @@ def classify(inputTree, featLabels, testVec):
> 使用算法: 此步骤可以适用于任何监督学习任务,而使用决策树可以更好地理解数据的内在含义。
-### 项目案例2: 使用决策树预测隐形眼镜类型
+## 4.2 项目案例2: 使用决策树预测隐形眼镜类型
-[完整代码地址](/src/py2.x/ml/3.DecisionTree/DecisionTree.py):
+[完整代码地址](../源代码)
-#### 项目概述
+### 项目概述
隐形眼镜类型包括硬材质、软材质以及不适合佩戴隐形眼镜。我们需要使用决策树预测患者需要佩戴的隐形眼镜类型。
-#### 开发流程
+### 开发流程
1. 收集数据: 提供的文本文件。
2. 解析数据: 解析 tab 键分隔的数据行
diff --git a/机器学习/殷康龙/机器学习笔记/4.朴素贝叶斯.md b/机器学习/殷康龙/机器学习笔记/4.朴素贝叶斯.md
index fa1bcf2e..edcdeff0 100644
--- a/机器学习/殷康龙/机器学习笔记/4.朴素贝叶斯.md
+++ b/机器学习/殷康龙/机器学习笔记/4.朴素贝叶斯.md
@@ -1,77 +1,78 @@
-
# 第4章 基于概率论的分类方法: 朴素贝叶斯
-## 朴素贝叶斯 概述
+## 1 朴素贝叶斯 概述
`贝叶斯分类是一类分类算法的总称,这类算法均以贝叶斯定理为基础,故统称为贝叶斯分类。本章首先介绍贝叶斯分类算法的基础——贝叶斯定理。最后,我们通过实例来讨论贝叶斯分类的中最简单的一种: 朴素贝叶斯分类。`
-## 贝叶斯理论 & 条件概率
+## 2 贝叶斯理论 & 条件概率
### 贝叶斯理论
-我们现在有一个数据集,它由两类数据组成,数据分布如下图所示:
+* 我们现在有一个数据集,它由两类数据组成,数据分布如下图所示:
-
+
-我们现在用 p1(x,y) 表示数据点 (x,y) 属于类别 1(图中用圆点表示的类别)的概率,用 p2(x,y) 表示数据点 (x,y) 属于类别 2(图中三角形表示的类别)的概率,那么对于一个新数据点 (x,y),可以用下面的规则来判断它的类别:
-* 如果 p1(x,y) > p2(x,y) ,那么类别为1
-* 如果 p2(x,y) > p1(x,y) ,那么类别为2
+* 我们现在用 p1(x,y) 表示数据点 (x,y) 属于类别 1(图中用圆点表示的类别)的概率,用 p2(x,y) 表示数据点 (x,y) 属于类别 2(图中三角形表示的类别)的概率,那么对于一个新数据点 (x,y),可以用下面的规则来判断它的类别:
+ * 如果 p1(x,y) > p2(x,y) ,那么类别为1
+ * 如果 p2(x,y) > p1(x,y) ,那么类别为2
-也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
+* 也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
### 条件概率
-如果你对 p(x,y|c1) 符号很熟悉,那么可以跳过本小节。
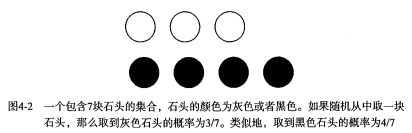
+* 有一个装了 7 块石头的罐子,其中 3 块是白色的,4 块是黑色的。如果从罐子中随机取出一块石头,那么是白色石头的可能性是多少?由于取石头有 7 种可能,其中 3 种为白色,所以取出白色石头的概率为 3/7 。那么取到黑色石头的概率又是多少呢?很显然,是 4/7 。我们使用 P(white) 来表示取到白色石头的概率,其概率值可以通过白色石头数目除以总的石头数目来得到。
+
-有一个装了 7 块石头的罐子,其中 3 块是白色的,4 块是黑色的。如果从罐子中随机取出一块石头,那么是白色石头的可能性是多少?由于取石头有 7 种可能,其中 3 种为白色,所以取出白色石头的概率为 3/7 。那么取到黑色石头的概率又是多少呢?很显然,是 4/7 。我们使用 P(white) 来表示取到白色石头的概率,其概率值可以通过白色石头数目除以总的石头数目来得到。
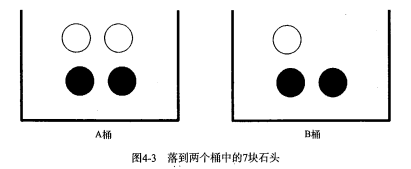
+* 如果这 7 块石头如下图所示,放在两个桶中,那么上述概率应该如何计算?
+
-
-
-如果这 7 块石头如下图所示,放在两个桶中,那么上述概率应该如何计算?
-
-
-
-计算 P(white) 或者 P(black) ,如果事先我们知道石头所在桶的信息是会改变结果的。这就是所谓的条件概率(conditional probablity)。假定计算的是从 B 桶取到白色石头的概率,这个概率可以记作 P(white|bucketB) ,我们称之为“在已知石头出自 B 桶的条件下,取出白色石头的概率”。很容易得到,P(white|bucketA) 值为 2/4 ,P(white|bucketB) 的值为 1/3 。
-
-条件概率的计算公式如下:
+* 计算 P(white) 或者 P(black) ,如果事先我们知道石头所在桶的信息是会改变结果的。这就是所谓的条件概率(conditional probablity)。假定计算的是从 B 桶取到白色石头的概率,这个概率可以记作 P(white|bucketB) ,我们称之为“在已知石头出自 B 桶的条件下,取出白色石头的概率”。很容易得到,P(white|bucketA) 值为 2/4 ,P(white|bucketB) 的值为 1/3 。
+* 条件概率的计算公式如下:
+$$
P(white|bucketB) = P(white and bucketB) / P(bucketB)
+$$
-首先,我们用 B 桶中白色石头的个数除以两个桶中总的石头数,得到 P(white and bucketB) = 1/7 .其次,由于 B 桶中有 3 块石头,而总石头数为 7 ,于是 P(bucketB) 就等于 3/7 。于是又 P(white|bucketB) = P(white and bucketB) / P(bucketB) = (1/7) / (3/7) = 1/3 。
+* 首先,我们用 B 桶中白色石头的个数除以两个桶中总的石头数,得到 P(white and bucketB) = 1/7 .其次,由于 B 桶中有 3 块石头,而总石头数为 7 ,于是 P(bucketB) 就等于 3/7 。于是又 P(white|bucketB) = P(white and bucketB) / P(bucketB) = (1/7) / (3/7) = 1/3 。
-另外一种有效计算条件概率的方法称为贝叶斯准则。贝叶斯准则告诉我们如何交换条件概率中的条件与结果,即如果已知 P(x|c),要求 P(c|x),那么可以使用下面的计算方法:
+* 另外一种有效计算条件概率的方法称为贝叶斯准则。贝叶斯准则告诉我们如何交换条件概率中的条件与结果,即如果已知 P(x|c),要求 P(c|x),那么可以使用下面的计算方法:
-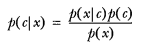
+$$
+p(c|x)=\frac{p(x|c)p(c)}{p(x)}
+$$
### 使用条件概率来分类
-上面我们提到贝叶斯决策理论要求计算两个概率 p1(x, y) 和 p2(x, y):
-* 如果 p1(x, y) > p2(x, y), 那么属于类别 1;
-* 如果 p2(x, y) > p1(X, y), 那么属于类别 2.
+* 上面我们提到贝叶斯决策理论要求计算两个概率 p1(x, y) 和 p2(x, y):
+ * 如果 p1(x, y) > p2(x, y), 那么属于类别 1;
+ * 如果 p2(x, y) > p1(x, y), 那么属于类别 2.
-这并不是贝叶斯决策理论的所有内容。使用 p1() 和 p2() 只是为了尽可能简化描述,而真正需要计算和比较的是 p(c1|x, y) 和 p(c2|x, y) .这些符号所代表的具体意义是: 给定某个由 x、y 表示的数据点,那么该数据点来自类别 c1 的概率是多少?数据点来自类别 c2 的概率又是多少?注意这些概率与概率 p(x, y|c1) 并不一样,不过可以使用贝叶斯准则来交换概率中条件与结果。具体地,应用贝叶斯准则得到:
+* 这并不是贝叶斯决策理论的所有内容。使用 p1() 和 p2() 只是为了尽可能简化描述,而真正需要计算和比较的是 p(c1|x, y) 和 p(c2|x, y) .这些符号所代表的具体意义是: 给定某个由 x、y 表示的数据点,那么该数据点来自类别 c1 的概率是多少?数据点来自类别 c2 的概率又是多少?
+* 注意这些概率与概率 p(x, y|c1) 并不一样,不过可以使用贝叶斯准则来交换概率中条件与结果。具体地,应用贝叶斯准则得到:
-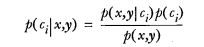
+$$
+p(c|x,y)=\frac{p(x,y|c)p(c)}{p(x,y)}
+$$
-使用上面这些定义,可以定义贝叶斯分类准则为:
-* 如果 P(c1|x, y) > P(c2|x, y), 那么属于类别 c1;
-* 如果 P(c2|x, y) > P(c1|x, y), 那么属于类别 c2.
+* 使用上面这些定义,可以定义贝叶斯分类准则为:
+ * 如果 P(c1|x, y) > P(c2|x, y), 那么属于类别 c1;
+ * 如果 P(c2|x, y) > P(c1|x, y), 那么属于类别 c2.
-在文档分类中,整个文档(如一封电子邮件)是实例,而电子邮件中的某些元素则构成特征。我们可以观察文档中出现的词,并把每个词作为一个特征,而每个词的出现或者不出现作为该特征的值,这样得到的特征数目就会跟词汇表中的词的数目一样多。
+* 在文档分类中,整个文档(如一封电子邮件)是实例,而电子邮件中的某些元素则构成特征。我们可以观察文档中出现的词,并把每个词作为一个特征,而每个词的出现或者不出现作为该特征的值,这样得到的特征数目就会跟词汇表中的词的数目一样多。
-我们假设特征之间 **相互独立** 。所谓 独立(independence) 指的是统计意义上的独立,即一个特征或者单词出现的可能性与它和其他单词相邻没有关系,比如说,“我们”中的“我”和“们”出现的概率与这两个字相邻没有任何关系。这个假设正是朴素贝叶斯分类器中 朴素(naive) 一词的含义。朴素贝叶斯分类器中的另一个假设是,每个特征同等重要。
+* 我们假设特征之间 **相互独立** 。所谓 独立(independence) 指的是统计意义上的独立,即一个特征或者单词出现的可能性与它和其他单词相邻没有关系,比如说,“我们”中的“我”和“们”出现的概率与这两个字相邻没有任何关系。这个假设正是朴素贝叶斯分类器中 朴素(naive) 一词的含义。朴素贝叶斯分类器中的另一个假设是,每个特征同等重要。
-Note: 朴素贝叶斯分类器通常有两种实现方式: 一种基于伯努利模型实现,一种基于多项式模型实现。这里采用前一种实现方式。该实现方式中并不考虑词在文档中出现的次数,只考虑出不出现,因此在这个意义上相当于假设词是等权重的。
+* Note: 朴素贝叶斯分类器通常有两种实现方式: 一种**基于伯努利模型实现(0、1)**,一种**基于多项式模型实现(0.1,0.4,0.5)**。这里采用前一种实现方式。该实现方式中并不考虑词在文档中出现的次数,只考虑出不出现,因此在这个意义上相当于假设词是等权重的。
-## 朴素贝叶斯 场景
+## 3 朴素贝叶斯 场景
-机器学习的一个重要应用就是文档的自动分类。
+* 机器学习的一个重要应用就是文档的自动分类。
-在文档分类中,整个文档(如一封电子邮件)是实例,而电子邮件中的某些元素则构成特征。我们可以观察文档中出现的词,并把每个词作为一个特征,而每个词的出现或者不出现作为该特征的值,这样得到的特征数目就会跟词汇表中的词的数目一样多。
+* 在文档分类中,整个文档(如一封电子邮件)是实例,而电子邮件中的某些元素则构成特征。我们可以观察文档中出现的词,并把每个词作为一个特征,而每个词的出现或者不出现作为该特征的值,这样得到的特征数目就会跟词汇表中的词的数目一样多。
-朴素贝叶斯是上面介绍的贝叶斯分类器的一个扩展,是用于文档分类的常用算法。下面我们会进行一些朴素贝叶斯分类的实践项目。
+* 朴素贝叶斯是上面介绍的贝叶斯分类器的一个扩展,是用于文档分类的常用算法。下面我们会进行一些朴素贝叶斯分类的实践项目。
-## 朴素贝叶斯 原理
+## 4 朴素贝叶斯 原理
### 朴素贝叶斯 工作原理
@@ -108,17 +109,17 @@ P(white|bucketB) = P(white and bucketB) / P(bucketB)
适用数据类型: 标称型数据。
```
-## 朴素贝叶斯 项目案例
+## 5 朴素贝叶斯 项目案例
-### 项目案例1: 屏蔽社区留言板的侮辱性言论
+## 5.1 项目案例1: 屏蔽社区留言板的侮辱性言论
-[完整代码地址](/src/py2.x/ml/4.NaiveBayes/bayes.py):
+[完整代码地址]()
-#### 项目概述
+### 项目概述
构建一个快速过滤器来屏蔽在线社区留言板上的侮辱性言论。如果某条留言使用了负面或者侮辱性的语言,那么就将该留言标识为内容不当。对此问题建立两个类别: 侮辱类和非侮辱类,使用 1 和 0 分别表示。
-#### 开发流程
+### 开发流程
```
收集数据: 可以使用任何方法
@@ -371,15 +372,15 @@ def testingNB():
```
-### 项目案例2: 使用朴素贝叶斯过滤垃圾邮件
+### 4.2 项目案例2: 使用朴素贝叶斯过滤垃圾邮件
-[完整代码地址](/src/py2.x/ml/4.NaiveBayes/bayes.py):
+[完整代码地址]()
-#### 项目概述
+### 项目概述
完成朴素贝叶斯的一个最著名的应用: 电子邮件垃圾过滤。
-#### 开发流程
+### 开发流程
使用朴素贝叶斯对电子邮件进行分类
@@ -536,9 +537,9 @@ def spamTest():
> 使用算法: 构建一个完整的程序对一组文档进行分类,将错分的文档输出到屏幕上
-### 项目案例3: 使用朴素贝叶斯分类器从个人广告中获取区域倾向
+### 4.3 项目案例3: 使用朴素贝叶斯分类器从个人广告中获取区域倾向
-[完整代码地址](/src/py2.x/ml/4.NaiveBayes/bayes.py):
+[完整代码地址]()
#### 项目概述
diff --git a/机器学习/殷康龙/机器学习笔记/5.Logistic回归.md b/机器学习/殷康龙/机器学习笔记/5.Logistic回归.md
index d3ee3711..7803d9a4 100644
--- a/机器学习/殷康龙/机器学习笔记/5.Logistic回归.md
+++ b/机器学习/殷康龙/机器学习笔记/5.Logistic回归.md
@@ -1,43 +1,45 @@
# 第5章 Logistic回归
-## Logistic 回归 概述
+## 1 Logistic 回归 概述
`Logistic 回归 或者叫逻辑回归 虽然名字有回归,但是它是用来做分类的。其主要思想是: 根据现有数据对分类边界线(Decision Boundary)建立回归公式,以此进行分类。`
-## 须知概念
+## 2 须知概念
### Sigmoid 函数
-#### 回归 概念
+* **回归 概念**
+ 假设现在有一些数据点,我们用一条直线对这些点进行拟合(这条直线称为最佳拟合直线),这个拟合的过程就叫做回归。进而可以得到对这些点的拟合直线方程,那么我们根据这个回归方程,怎么进行分类呢?请看下面。
-假设现在有一些数据点,我们用一条直线对这些点进行拟合(这条直线称为最佳拟合直线),这个拟合的过程就叫做回归。进而可以得到对这些点的拟合直线方程,那么我们根据这个回归方程,怎么进行分类呢?请看下面。
+* **二值型输出分类函数**
+ 我们想要的函数应该是: 能接受所有的输入然后预测出类别。例如,在两个类的情况下,上述函数输出 0 或 1.或许你之前接触过具有这种性质的函数,该函数称为 `海维塞得阶跃函数(Heaviside step function)`,或者直接称为 `单位阶跃函数`。然而,海维塞得阶跃函数的问题在于: 该函数在跳跃点上从 0 瞬间跳跃到 1,这个瞬间跳跃过程有时很难处理。幸好,另一个函数也有类似的性质(可以输出 0 或者 1 的性质),且数学上更易处理,这就是 Sigmoid 函数。 Sigmoid 函数具体的计算公式如下:
-#### 二值型输出分类函数
-我们想要的函数应该是: 能接受所有的输入然后预测出类别。例如,在两个类的情况下,上述函数输出 0 或 1.或许你之前接触过具有这种性质的函数,该函数称为 `海维塞得阶跃函数(Heaviside step function)`,或者直接称为 `单位阶跃函数`。然而,海维塞得阶跃函数的问题在于: 该函数在跳跃点上从 0 瞬间跳跃到 1,这个瞬间跳跃过程有时很难处理。幸好,另一个函数也有类似的性质(可以输出 0 或者 1 的性质),且数学上更易处理,这就是 Sigmoid 函数。 Sigmoid 函数具体的计算公式如下:
+$$
+\sigma(z)=\frac{1}{1+e^{-z}}
+$$
-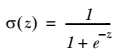
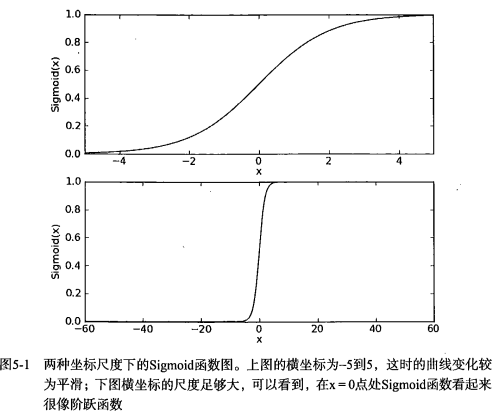
+* 下图给出了 Sigmoid 函数在不同坐标尺度下的两条曲线图。当 x 为 0 时,Sigmoid 函数值为 0.5 。随着 x 的增大,对应的 Sigmoid 值将逼近于 1 ; 而随着 x 的减小, Sigmoid 值将逼近于 0 。如果横坐标刻度足够大, Sigmoid 函数看起来很像一个阶跃函数。
-下图给出了 Sigmoid 函数在不同坐标尺度下的两条曲线图。当 x 为 0 时,Sigmoid 函数值为 0.5 。随着 x 的增大,对应的 Sigmoid 值将逼近于 1 ; 而随着 x 的减小, Sigmoid 值将逼近于 0 。如果横坐标刻度足够大, Sigmoid 函数看起来很像一个阶跃函数。
+
-
-
-因此,为了实现 Logistic 回归分类器,我们可以在每个特征上都乘以一个回归系数(如下公式所示),然后把所有结果值相加,将这个总和代入 Sigmoid 函数中,进而得到一个范围在 0~1 之间的数值。任何大于 0.5 的数据被分入 1 类,小于 0.5 即被归入 0 类。所以,Logistic 回归也是一种概率估计,比如这里Sigmoid 函数得出的值为0.5,可以理解为给定数据和参数,数据被分入 1 类的概率为0.5。想对Sigmoid 函数有更多了解,可以点开[此链接](https://www.desmos.com/calculator/bgontvxotm)跟此函数互动。
+* 因此,为了实现 Logistic 回归分类器,我们可以在每个特征上都乘以一个回归系数(如下公式所示),然后把所有结果值相加,将这个总和代入 Sigmoid 函数中,进而得到一个范围在 0~1 之间的数值。任何大于 0.5 的数据被分入 1 类,小于 0.5 即被归入 0 类。所以,Logistic 回归也是一种概率估计,比如这里Sigmoid 函数得出的值为0.5,可以理解为给定数据和参数,数据被分入 1 类的概率为0.5。
### 基于最优化方法的回归系数确定
-Sigmoid 函数的输入记为 z ,由下面公式得到:
+* Sigmoid 函数的输入记为 z ,由下面公式得到:
-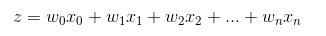
+$$z=w^T*x +b$$
-如果采用向量的写法,上述公式可以写成 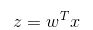 ,它表示将这两个数值向量对应元素相乘然后全部加起来即得到 z 值。其中的向量 x 是分类器的输入数据,向量 w 也就是我们要找到的最佳参数(系数),从而使得分类器尽可能地精确。为了寻找该最佳参数,需要用到最优化理论的一些知识。我们这里使用的是——梯度上升法(Gradient Ascent)。
+
+* 它表示将这两个数值向量对应元素相乘然后全部加起来即得到 z 值。其中的向量 x 是分类器的输入数据,向量 w 也就是我们要找到的最佳参数(系数),从而使得分类器尽可能地精确。为了寻找该最佳参数,需要用到最优化理论的一些知识。我们这里使用的是——梯度上升法(Gradient Ascent)。
### 梯度上升法
-#### 梯度的介绍
-需要一点点向量方面的数学知识
+* **梯度的介绍**
+ 需要一点点向量方面的数学知识
```
向量 = 值 + 方向
@@ -45,24 +47,27 @@ Sigmoid 函数的输入记为 z ,由下面公式得到:
梯度 = 梯度值 + 梯度方向
```
-#### 梯度上升法的思想
+* **梯度上升法的思想**
要找到某函数的最大值,最好的方法是沿着该函数的梯度方向探寻。如果梯度记为 ▽ ,则函数 f(x, y) 的梯度由下式表示:
-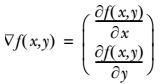
+$$
+d f(x,y) = \left\{ \frac{\partial f(x,y)}{\partial x} ,\\ \frac{\partial f(x,y)}{\partial y} \right\}
+$$
-这个梯度意味着要沿 x 的方向移动 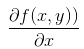 ,沿 y 的方向移动 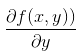 。其中,函数f(x, y) 必须要在待计算的点上有定义并且可微。下图是一个具体的例子。
-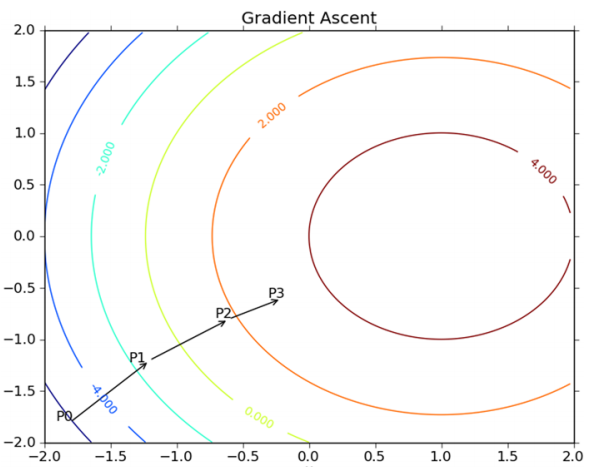
+* 这个梯度意味着要沿 x 的方向移动$\frac{\partial f(x,y)}{\partial x}$,沿 y 的方向移动$\frac{\partial f(x,y)}{\partial y}$ 。其中,函数f(x, y) 必须要在待计算的点上有定义并且可微。下图是一个具体的例子。
-上图展示的,梯度上升算法到达每个点后都会重新估计移动的方向。从 P0 开始,计算完该点的梯度,函数就根据梯度移动到下一点 P1。在 P1 点,梯度再次被重新计算,并沿着新的梯度方向移动到 P2 。如此循环迭代,直到满足停止条件。迭代过程中,梯度算子总是保证我们能选取到最佳的移动方向。
+
-上图中的梯度上升算法沿梯度方向移动了一步。可以看到,梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向,而未提到移动量的大小。该量值称为步长,记作 α 。用向量来表示的话,梯度上升算法的迭代公式如下:
+* 上图展示的,梯度上升算法到达每个点后都会重新估计移动的方向。从 P0 开始,计算完该点的梯度,函数就根据梯度移动到下一点 P1。在 P1 点,梯度再次被重新计算,并沿着新的梯度方向移动到 P2 。如此循环迭代,直到满足停止条件。迭代过程中,梯度算子总是保证我们能选取到最佳的移动方向。
-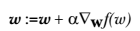
+* 上图中的梯度上升算法沿梯度方向移动了一步。可以看到,梯度算子总是指向函数值增长最快的方向。这里所说的是移动方向,而未提到移动量的大小。该量值称为步长,记作 α 。用向量来表示的话,梯度上升算法的迭代公式如下:
-该公式将一直被迭代执行,直至达到某个停止条件为止,比如迭代次数达到某个指定值或者算法达到某个可以允许的误差范围。
+$$
+w:= w+ \alpha \nabla_wf(w)
+$$
-介绍一下几个相关的概念:
+* 该公式将一直被迭代执行,直至达到某个停止条件为止,比如迭代次数达到某个指定值或者算法达到某个可以允许的误差范围。介绍一下几个相关的概念:
```
例如: y = w0 + w1x1 + w2x2 + ... + wnxn
梯度: 参考上图的例子,二维图像,x方向代表第一个系数,也就是 w1,y方向代表第二个系数也就是 w2,这样的向量就是梯度。
@@ -72,26 +77,24 @@ Sigmoid 函数的输入记为 z ,由下面公式得到:
```
- 问: 有人会好奇为什么有些书籍上说的是梯度下降法(Gradient Decent)?
-
- 答: 其实这个两个方法在此情况下本质上是相同的。关键在于代价函数(cost function)或者叫目标函数(objective function)。如果目标函数是损失函数,那就是最小化损失函数来求函数的最小值,就用梯度下降。 如果目标函数是似然函数(Likelihood function),就是要最大化似然函数来求函数的最大值,那就用梯度上升。在逻辑回归中, 损失函数和似然函数无非就是互为正负关系。
-
- 只需要在迭代公式中的加法变成减法。因此,对应的公式可以写成
-
-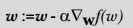
+> 问: 有人会好奇为什么有些书籍上说的是梯度下降法(Gradient Decent)?
+>
+> 答: 其实这个两个方法在此情况下本质上是相同的。关键在于代价函数(cost function)或者叫目标函数(objective function)。如果目标函数是损失函数,那就是最小化损失函数来求函数的最小值,就用梯度下降。 如果目标函数是似然函数(Likelihood function),就是要最大化似然函数来求函数的最大值,那就用梯度上升。在逻辑回归中, 损失函数和似然函数无非就是互为正负关系。
+> 只需要在迭代公式中的加法变成减法。因此,对应的公式可以写成
-**局部最优现象 (Local Optima)**
+
+* **局部最优现象 (Local Optima)**
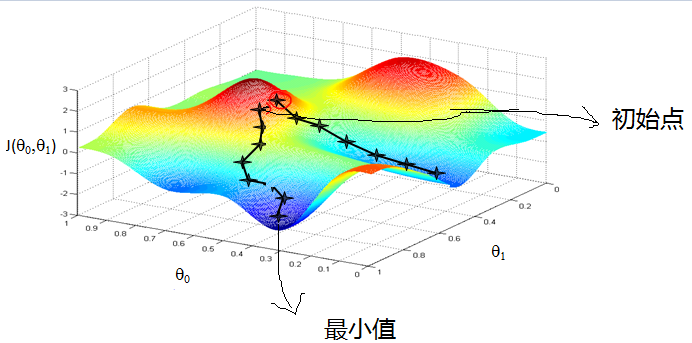
-上图表示参数 θ 与误差函数 J(θ) 的关系图 (这里的误差函数是损失函数,所以我们要最小化损失函数),红色的部分是表示 J(θ) 有着比较高的取值,我们需要的是,能够让 J(θ) 的值尽量的低。也就是深蓝色的部分。θ0,θ1 表示 θ 向量的两个维度(此处的θ0,θ1是x0和x1的系数,也对应的是上文w0和w1)。
+* 上图表示参数 θ 与误差函数 J(θ) 的关系图 (这里的误差函数是损失函数,所以我们要最小化损失函数),红色的部分是表示 J(θ) 有着比较高的取值,我们需要的是,能够让 J(θ) 的值尽量的低。也就是深蓝色的部分。θ0,θ1 表示 θ 向量的两个维度(此处的θ0,θ1是x0和x1的系数,也对应的是上文w0和w1)。
-可能梯度下降的最终点并非是全局最小点,可能是一个局部最小点,如我们上图中的右边的梯度下降曲线,描述的是最终到达一个局部最小点,这是我们重新选择了一个初始点得到的。
+* 可能梯度下降的最终点并非是全局最小点,可能是一个局部最小点,如我们上图中的右边的梯度下降曲线,描述的是最终到达一个局部最小点,这是我们重新选择了一个初始点得到的。
-看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点。
+* 看来我们这个算法将会在很大的程度上被初始点的选择影响而陷入局部最小点。
-## Logistic 回归 原理
+## 3 Logistic 回归 原理
### Logistic 回归 工作原理
@@ -122,21 +125,18 @@ Sigmoid 函数的输入记为 z ,由下面公式得到:
适用数据类型: 数值型和标称型数据。
```
-### 附加 方向导数与梯度
-
+## 4 Logistic 回归 项目案例
-## Logistic 回归 项目案例
+## 4.1 项目案例1: 使用 Logistic 回归在简单数据集上的分类
-### 项目案例1: 使用 Logistic 回归在简单数据集上的分类
+[完整代码地址](/5.Logistic/logistic.py)
-[完整代码地址](/src/py2.x/ml/5.Logistic/logistic.py):
-
-#### 项目概述
+## 项目概述
在一个简单的数据集上,采用梯度上升法找到 Logistic 回归分类器在此数据集上的最佳回归系数
-#### 开发流程
+## 开发流程
```
收集数据: 可以使用任何方法
@@ -313,7 +313,7 @@ def testLR():
> 使用算法: 对简单数据集中数据进行分类
-#### 注意
+### 注意
梯度上升算法在每次更新回归系数时都需要遍历整个数据集,该方法在处理 100 个左右的数据集时尚可,但如果有数十亿样本和成千上万的特征,那么该方法的计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数,该方法称为 `随机梯度上升算法`。由于可以在新样本到来时对分类器进行增量式更新,因而随机梯度上升算法是一个在线学习(online learning)算法。与 “在线学习” 相对应,一次处理所有数据被称作是 “批处理” (batch) 。
diff --git a/机器学习/殷康龙/机器学习笔记/image/2021-03-20-13-38-42.png b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-13-38-42.png
new file mode 100644
index 00000000..afac0ee4
Binary files /dev/null and b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-13-38-42.png differ
diff --git a/机器学习/殷康龙/机器学习笔记/image/2021-03-20-13-57-22.png b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-13-57-22.png
new file mode 100644
index 00000000..d8d72754
Binary files /dev/null and b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-13-57-22.png differ
diff --git a/机器学习/殷康龙/机器学习笔记/image/2021-03-20-14-31-12.png b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-14-31-12.png
new file mode 100644
index 00000000..77f9e2ab
Binary files /dev/null and b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-14-31-12.png differ
diff --git a/机器学习/殷康龙/机器学习笔记/image/2021-03-20-14-48-47.png b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-14-48-47.png
new file mode 100644
index 00000000..a6868b42
Binary files /dev/null and b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-14-48-47.png differ
diff --git a/机器学习/殷康龙/机器学习笔记/image/2021-03-20-15-01-20.png b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-15-01-20.png
new file mode 100644
index 00000000..3d277cbe
Binary files /dev/null and b/机器学习/殷康龙/机器学习笔记/image/2021-03-20-15-01-20.png differ
diff --git a/概率论与数理统计/第1节 概率论基础知识.md b/概率论与数理统计/第1节 概率论基础知识.md
index e945b90a..eef29d36 100644
--- a/概率论与数理统计/第1节 概率论基础知识.md
+++ b/概率论与数理统计/第1节 概率论基础知识.md
@@ -21,6 +21,10 @@
$$
P(B|A)=\frac{P(AB)}{P(A)}
$$
+也是一种链式法则。图解的方式理解。
+$$
+P(B|A)=\frac{P(AB|1)}{P(A|1)}
+$$
在事件A发生的条件下,事件B发生的概率。
### 性质
@@ -32,6 +36,10 @@ $$
$$
P(AB)=P(A)P(B|A)
$$
+也是一种链式法则。图解的方式理解。
+$$
+P(AB|1)=P(A|1)P(B|A)
+$$
### 全概率公式
设试验$E$样本空间为$S$,$A$为试验的实践,$B_1,\dotsm,B_n$为S的一个划分,且$P(B_i)>0$,则:
@@ -45,7 +53,7 @@ $$
$$
P(B_i|A)=\frac{P(A|B_i)P(B_i)}{\sum_{j=1}^nP(A|B_j)P(B_j)}
$$
-
+> 起到了交换条件与结果的作用。
## 1.4 独立性
### 定义
如果A,B是两个事件,满足: