# Queue
A queue is a linear data structure that follows the First In First Out (FIFO) rule. As the name suggests, a queue simulates the phenomenon of lining up, where newcomers continuously join the end of the queue, while people at the front of the queue leave one by one.
As shown in the figure below, we call the front of the queue the "front" and the end the "rear." The operation of adding an element to the rear is called "enqueue," and the operation of removing the front element is called "dequeue."

## Common Queue Operations
The common operations on a queue are shown in the table below. Note that method names may vary across different programming languages. We adopt the same naming convention as for stacks here.
Table Efficiency of Queue Operations
| Method | Description | Time Complexity |
| -------- | ------------------------------------------ | --------------- |
| `push()` | Enqueue element, add element to rear | $O(1)$ |
| `pop()` | Dequeue front element | $O(1)$ |
| `peek()` | Access front element | $O(1)$ |
We can directly use the ready-made queue classes in programming languages:
=== "Python"
```python title="queue.py"
from collections import deque
# Initialize queue
# In Python, we generally use the deque class as a queue
# Although queue.Queue() is a pure queue class, it is not very user-friendly, so it is not recommended
que: deque[int] = deque()
# Enqueue elements
que.append(1)
que.append(3)
que.append(2)
que.append(5)
que.append(4)
# Access front element
front: int = que[0]
# Dequeue element
pop: int = que.popleft()
# Get queue length
size: int = len(que)
# Check if queue is empty
is_empty: bool = len(que) == 0
```
=== "C++"
```cpp title="queue.cpp"
/* Initialize queue */
queue queue;
/* Enqueue elements */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);
/* Access front element */
int front = queue.front();
/* Dequeue element */
queue.pop();
/* Get queue length */
int size = queue.size();
/* Check if queue is empty */
bool empty = queue.empty();
```
=== "Java"
```java title="queue.java"
/* Initialize queue */
Queue queue = new LinkedList<>();
/* Enqueue elements */
queue.offer(1);
queue.offer(3);
queue.offer(2);
queue.offer(5);
queue.offer(4);
/* Access front element */
int peek = queue.peek();
/* Dequeue element */
int pop = queue.poll();
/* Get queue length */
int size = queue.size();
/* Check if queue is empty */
boolean isEmpty = queue.isEmpty();
```
=== "C#"
```csharp title="queue.cs"
/* Initialize queue */
Queue queue = new();
/* Enqueue elements */
queue.Enqueue(1);
queue.Enqueue(3);
queue.Enqueue(2);
queue.Enqueue(5);
queue.Enqueue(4);
/* Access front element */
int peek = queue.Peek();
/* Dequeue element */
int pop = queue.Dequeue();
/* Get queue length */
int size = queue.Count;
/* Check if queue is empty */
bool isEmpty = queue.Count == 0;
```
=== "Go"
```go title="queue_test.go"
/* Initialize queue */
// In Go, use list as a queue
queue := list.New()
/* Enqueue elements */
queue.PushBack(1)
queue.PushBack(3)
queue.PushBack(2)
queue.PushBack(5)
queue.PushBack(4)
/* Access front element */
peek := queue.Front()
/* Dequeue element */
pop := queue.Front()
queue.Remove(pop)
/* Get queue length */
size := queue.Len()
/* Check if queue is empty */
isEmpty := queue.Len() == 0
```
=== "Swift"
```swift title="queue.swift"
/* Initialize queue */
// Swift does not have a built-in queue class, can use Array as a queue
var queue: [Int] = []
/* Enqueue elements */
queue.append(1)
queue.append(3)
queue.append(2)
queue.append(5)
queue.append(4)
/* Access front element */
let peek = queue.first!
/* Dequeue element */
// Since it's an array, removeFirst has O(n) complexity
let pool = queue.removeFirst()
/* Get queue length */
let size = queue.count
/* Check if queue is empty */
let isEmpty = queue.isEmpty
```
=== "JS"
```javascript title="queue.js"
/* Initialize queue */
// JavaScript does not have a built-in queue, can use Array as a queue
const queue = [];
/* Enqueue elements */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);
/* Access front element */
const peek = queue[0];
/* Dequeue element */
// The underlying structure is an array, so shift() has O(n) time complexity
const pop = queue.shift();
/* Get queue length */
const size = queue.length;
/* Check if queue is empty */
const empty = queue.length === 0;
```
=== "TS"
```typescript title="queue.ts"
/* Initialize queue */
// TypeScript does not have a built-in queue, can use Array as a queue
const queue: number[] = [];
/* Enqueue elements */
queue.push(1);
queue.push(3);
queue.push(2);
queue.push(5);
queue.push(4);
/* Access front element */
const peek = queue[0];
/* Dequeue element */
// The underlying structure is an array, so shift() has O(n) time complexity
const pop = queue.shift();
/* Get queue length */
const size = queue.length;
/* Check if queue is empty */
const empty = queue.length === 0;
```
=== "Dart"
```dart title="queue.dart"
/* Initialize queue */
// In Dart, the Queue class is a deque and can also be used as a queue
Queue queue = Queue();
/* Enqueue elements */
queue.add(1);
queue.add(3);
queue.add(2);
queue.add(5);
queue.add(4);
/* Access front element */
int peek = queue.first;
/* Dequeue element */
int pop = queue.removeFirst();
/* Get queue length */
int size = queue.length;
/* Check if queue is empty */
bool isEmpty = queue.isEmpty;
```
=== "Rust"
```rust title="queue.rs"
/* Initialize deque */
// In Rust, use deque as a regular queue
let mut deque: VecDeque = VecDeque::new();
/* Enqueue elements */
deque.push_back(1);
deque.push_back(3);
deque.push_back(2);
deque.push_back(5);
deque.push_back(4);
/* Access front element */
if let Some(front) = deque.front() {
}
/* Dequeue element */
if let Some(pop) = deque.pop_front() {
}
/* Get queue length */
let size = deque.len();
/* Check if queue is empty */
let is_empty = deque.is_empty();
```
=== "C"
```c title="queue.c"
// C does not provide a built-in queue
```
=== "Kotlin"
```kotlin title="queue.kt"
/* Initialize queue */
val queue = LinkedList()
/* Enqueue elements */
queue.offer(1)
queue.offer(3)
queue.offer(2)
queue.offer(5)
queue.offer(4)
/* Access front element */
val peek = queue.peek()
/* Dequeue element */
val pop = queue.poll()
/* Get queue length */
val size = queue.size
/* Check if queue is empty */
val isEmpty = queue.isEmpty()
```
=== "Ruby"
```ruby title="queue.rb"
# Initialize queue
# Ruby's built-in queue (Thread::Queue) does not have peek and traversal methods, can use Array as a queue
queue = []
# Enqueue elements
queue.push(1)
queue.push(3)
queue.push(2)
queue.push(5)
queue.push(4)
# Access front element
peek = queue.first
# Dequeue element
# Please note that since it's an array, Array#shift has O(n) time complexity
pop = queue.shift
# Get queue length
size = queue.length
# Check if queue is empty
is_empty = queue.empty?
```
??? pythontutor "Code Visualization"
https://pythontutor.com/render.html#code=from%20collections%20import%20deque%0A%0A%22%22%22Driver%20Code%22%22%22%0Aif%20__name__%20%3D%3D%20%22__main__%22%3A%0A%20%20%20%20%23%20%E5%88%9D%E5%A7%8B%E5%8C%96%E9%98%9F%E5%88%97%0A%20%20%20%20%23%20%E5%9C%A8%20Python%20%E4%B8%AD%EF%BC%8C%E6%88%91%E4%BB%AC%E4%B8%80%E8%88%AC%E5%B0%86%E5%8F%8C%E5%90%91%E9%98%9F%E5%88%97%E7%B1%BB%20deque%20%E7%9C%8B%E4%BD%9C%E9%98%9F%E5%88%97%E4%BD%BF%E7%94%A8%0A%20%20%20%20%23%20%E8%99%BD%E7%84%B6%20queue.Queue%28%29%20%E6%98%AF%E7%BA%AF%E6%AD%A3%E7%9A%84%E9%98%9F%E5%88%97%E7%B1%BB%EF%BC%8C%E4%BD%86%E4%B8%8D%E5%A4%AA%E5%A5%BD%E7%94%A8%0A%20%20%20%20que%20%3D%20deque%28%29%0A%0A%20%20%20%20%23%20%E5%85%83%E7%B4%A0%E5%85%A5%E9%98%9F%0A%20%20%20%20que.append%281%29%0A%20%20%20%20que.append%283%29%0A%20%20%20%20que.append%282%29%0A%20%20%20%20que.append%285%29%0A%20%20%20%20que.append%284%29%0A%20%20%20%20print%28%22%E9%98%9F%E5%88%97%20que%20%3D%22,%20que%29%0A%0A%20%20%20%20%23%20%E8%AE%BF%E9%97%AE%E9%98%9F%E9%A6%96%E5%85%83%E7%B4%A0%0A%20%20%20%20front%20%3D%20que%5B0%5D%0A%20%20%20%20print%28%22%E9%98%9F%E9%A6%96%E5%85%83%E7%B4%A0%20front%20%3D%22,%20front%29%0A%0A%20%20%20%20%23%20%E5%85%83%E7%B4%A0%E5%87%BA%E9%98%9F%0A%20%20%20%20pop%20%3D%20que.popleft%28%29%0A%20%20%20%20print%28%22%E5%87%BA%E9%98%9F%E5%85%83%E7%B4%A0%20pop%20%3D%22,%20pop%29%0A%20%20%20%20print%28%22%E5%87%BA%E9%98%9F%E5%90%8E%20que%20%3D%22,%20que%29%0A%0A%20%20%20%20%23%20%E8%8E%B7%E5%8F%96%E9%98%9F%E5%88%97%E7%9A%84%E9%95%BF%E5%BA%A6%0A%20%20%20%20size%20%3D%20len%28que%29%0A%20%20%20%20print%28%22%E9%98%9F%E5%88%97%E9%95%BF%E5%BA%A6%20size%20%3D%22,%20size%29%0A%0A%20%20%20%20%23%20%E5%88%A4%E6%96%AD%E9%98%9F%E5%88%97%E6%98%AF%E5%90%A6%E4%B8%BA%E7%A9%BA%0A%20%20%20%20is_empty%20%3D%20len%28que%29%20%3D%3D%200%0A%20%20%20%20print%28%22%E9%98%9F%E5%88%97%E6%98%AF%E5%90%A6%E4%B8%BA%E7%A9%BA%20%3D%22,%20is_empty%29&cumulative=false&curInstr=3&heapPrimitives=nevernest&mode=display&origin=opt-frontend.js&py=311&rawInputLstJSON=%5B%5D&textReferences=false
## Queue Implementation
To implement a queue, we need a data structure that allows adding elements at one end and removing elements at the other end. Both linked lists and arrays meet this requirement.
### Linked List Implementation
As shown in the figure below, we can treat the "head node" and "tail node" of a linked list as the "front" and "rear" of the queue, respectively, with the rule that nodes can only be added at the rear and removed from the front.
=== "LinkedListQueue"

=== "push()"

=== "pop()"

Below is the code for implementing a queue using a linked list:
```src
[file]{linkedlist_queue}-[class]{linked_list_queue}-[func]{}
```
### Array Implementation
Deleting the first element in an array has a time complexity of $O(n)$, which would make the dequeue operation inefficient. However, we can use the following clever method to avoid this problem.
We can use a variable `front` to point to the index of the front element and maintain a variable `size` to record the queue length. We define `rear = front + size`, which calculates the position right after the rear element.
Based on this design, **the valid interval containing elements in the array is `[front, rear - 1]`**. The implementation methods for various operations are shown in the figure below:
- Enqueue operation: Assign the input element to the `rear` index and increase `size` by 1.
- Dequeue operation: Simply increase `front` by 1 and decrease `size` by 1.
As you can see, both enqueue and dequeue operations require only one operation, with a time complexity of $O(1)$.
=== "ArrayQueue"

=== "push()"

=== "pop()"
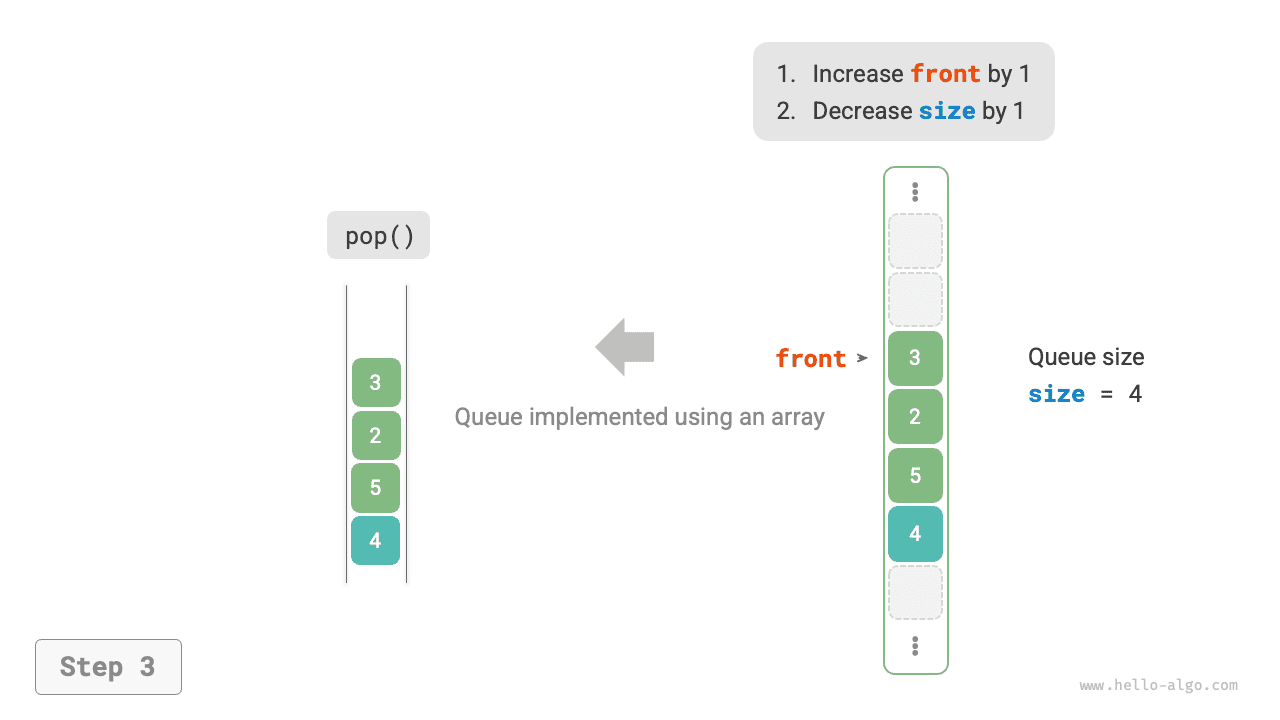
You may notice a problem: as we continuously enqueue and dequeue, both `front` and `rear` move to the right. **When they reach the end of the array, they cannot continue moving**. To solve this problem, we can treat the array as a "circular array" with head and tail connected.
For a circular array, we need to let `front` or `rear` wrap around to the beginning of the array when they cross the end. This periodic pattern can be implemented using the "modulo operation," as shown in the code below:
```src
[file]{array_queue}-[class]{array_queue}-[func]{}
```
The queue implemented above still has limitations: its length is immutable. However, this problem is not difficult to solve. We can replace the array with a dynamic array to introduce an expansion mechanism. Interested readers can try to implement this themselves.
The comparison conclusions for the two implementations are consistent with those for stacks and will not be repeated here.
## Typical Applications of Queue
- **Taobao orders**. After shoppers place orders, the orders are added to a queue, and the system subsequently processes the orders in the queue according to their sequence. During Double Eleven, massive orders are generated in a short time, and high concurrency becomes a key challenge that engineers need to tackle.
- **Various to-do tasks**. Any scenario that needs to implement "first come, first served" functionality, such as a printer's task queue or a restaurant's order queue, can effectively maintain the processing order using queues.