更新图床

problems/周总结/20201112回溯周末总结.md

@@ -1,5 +1,4 @@
 
-
 # 本周小结！（回溯算法系列三）
 
 ## 周一
@@ -12,14 +11,14 @@
 
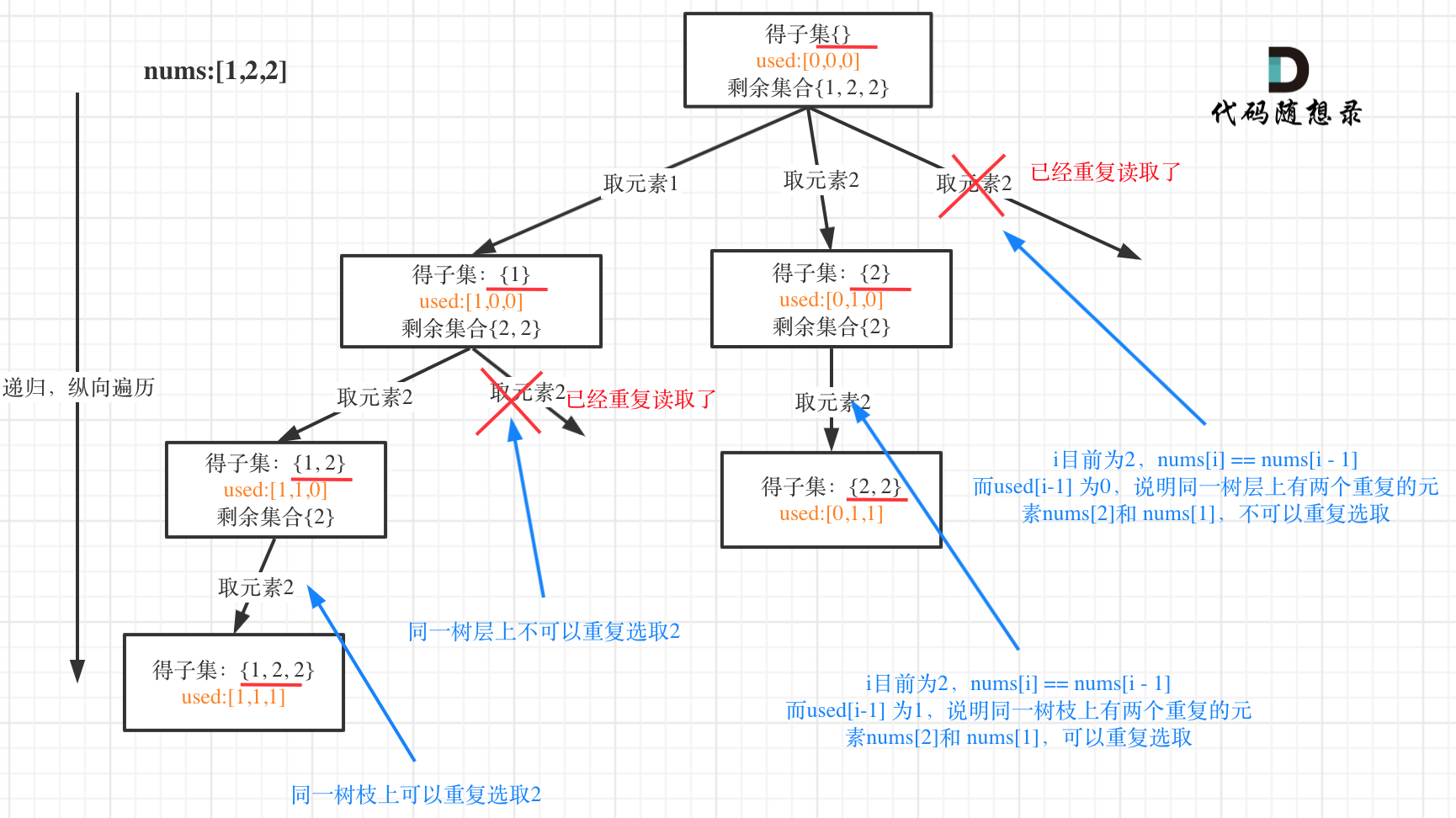
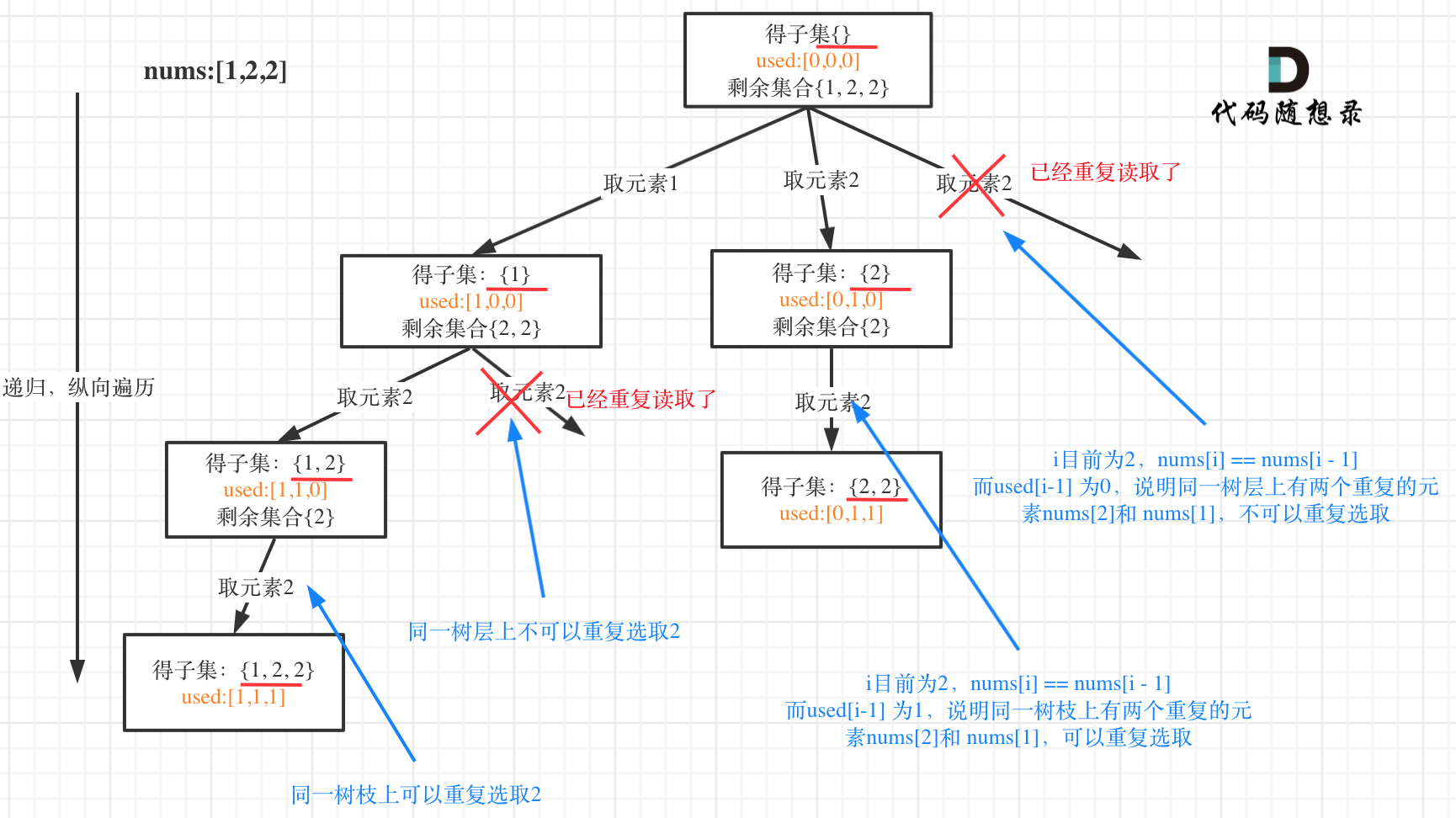
 树形结构如下：
 
-![90.子集II](https://img-blog.csdnimg.cn/2020111217110449.png)
+![90.子集II](https://code-thinking-1253855093.file.myqcloud.com/pics/2020111217110449-20230310133150714.png)
 
 ## 周二
 
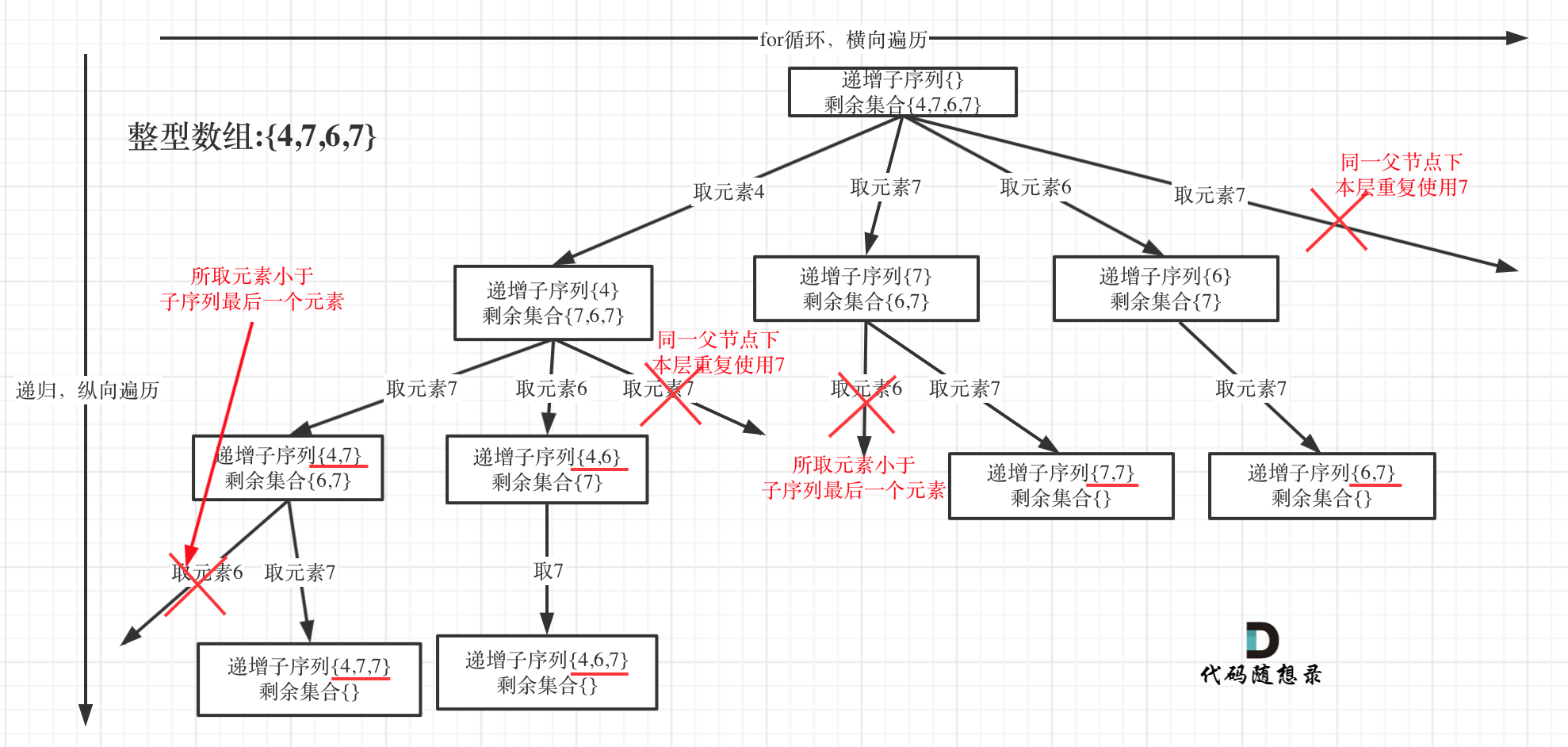
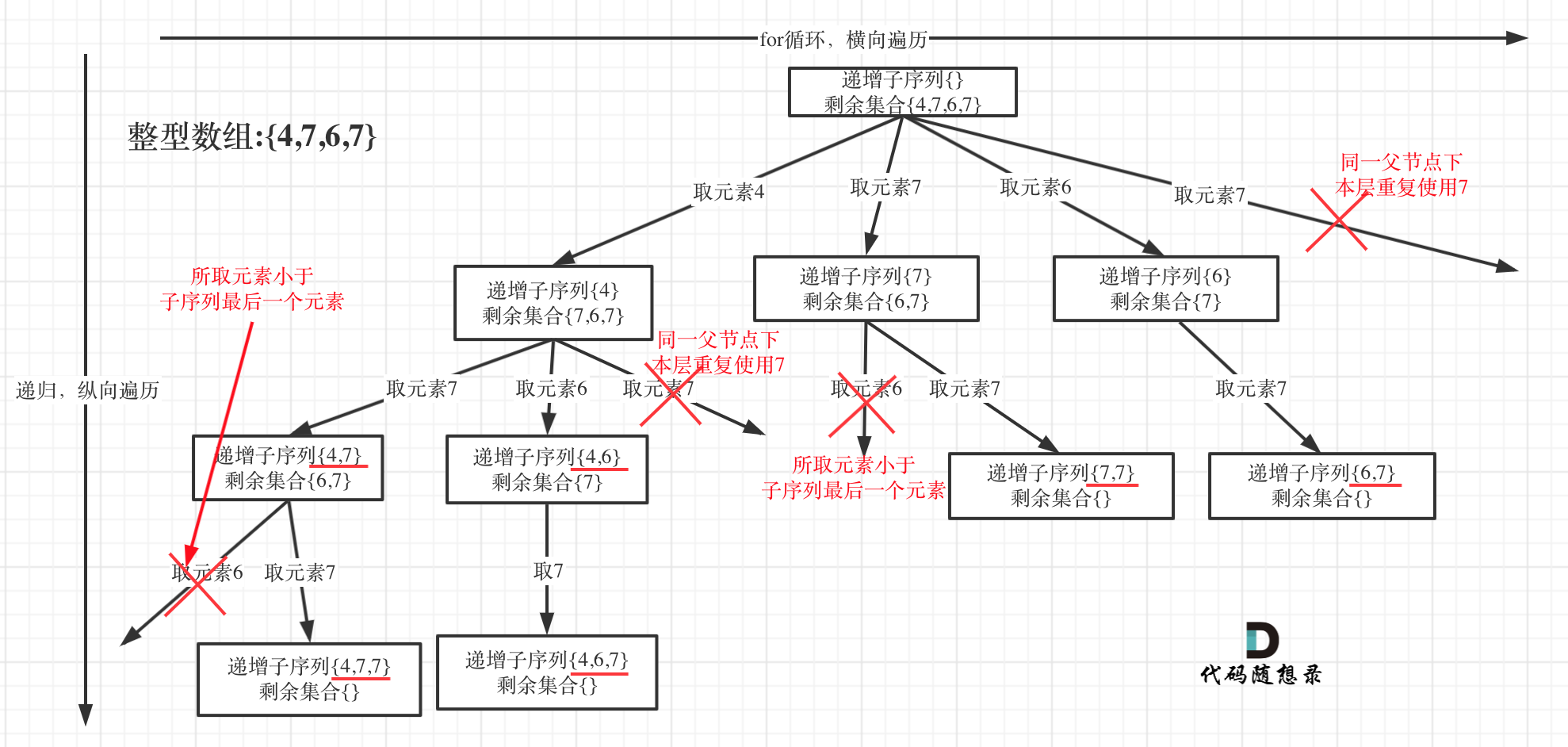
 在[回溯算法：递增子序列](https://programmercarl.com/0491.递增子序列.html)中，处处都能看到子集的身影，但处处是陷阱，值得好好琢磨琢磨！
 
 树形结构如下：
-![491. 递增子序列1](https://img-blog.csdnimg.cn/20201112170832333.png)
+![491. 递增子序列1](https://code-thinking-1253855093.file.myqcloud.com/pics/20201112170832333-20230310133155209.png)
 
 [回溯算法：递增子序列](https://programmercarl.com/0491.递增子序列.html)留言区大家有很多疑问，主要还是和[回溯算法：求子集问题（二）](https://programmercarl.com/0090.子集II.html)混合在了一起。
 
@@ -34,7 +33,7 @@
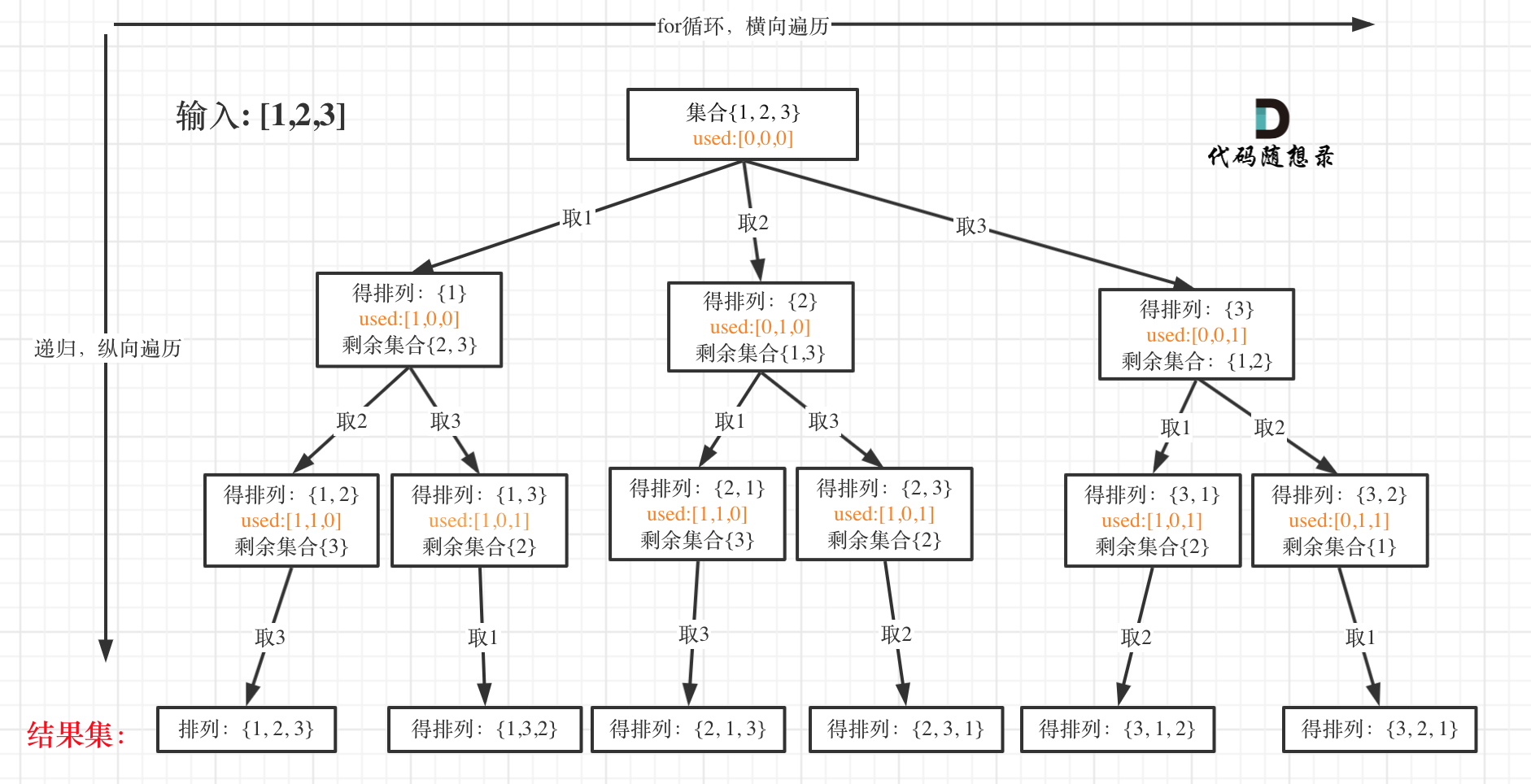
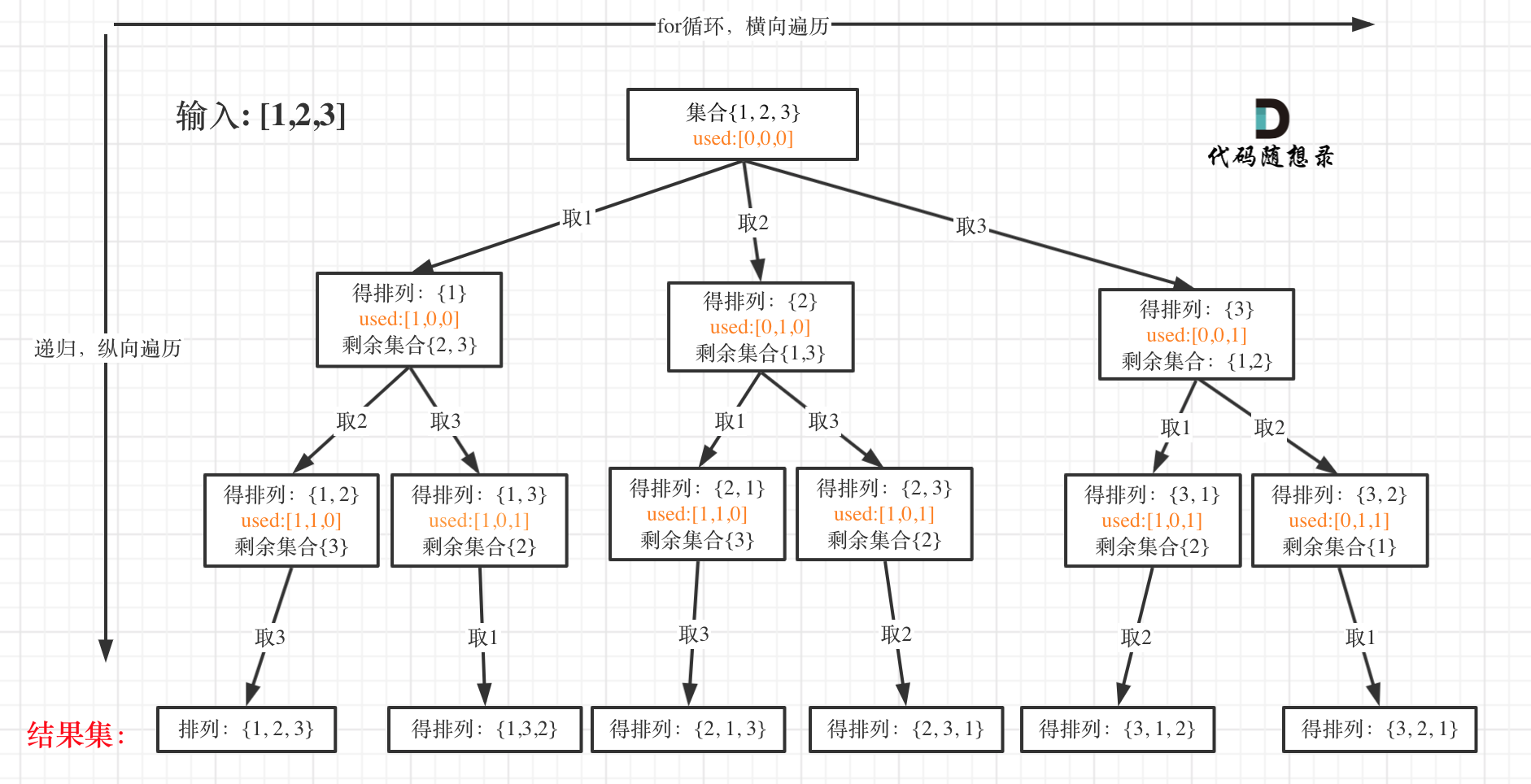
 可以看出元素1在[1,2]中已经使用过了，但是在[2,1]中还要在使用一次1，所以处理排列问题就不用使用startIndex了。
 
 如图：
-![46.全排列](https://img-blog.csdnimg.cn/20201112170304979.png)
+![46.全排列](https://code-thinking-1253855093.file.myqcloud.com/pics/20201112170304979-20230310133201250.png)
 
 **大家此时可以感受出排列问题的不同：**
 
@@ -47,7 +46,7 @@
 
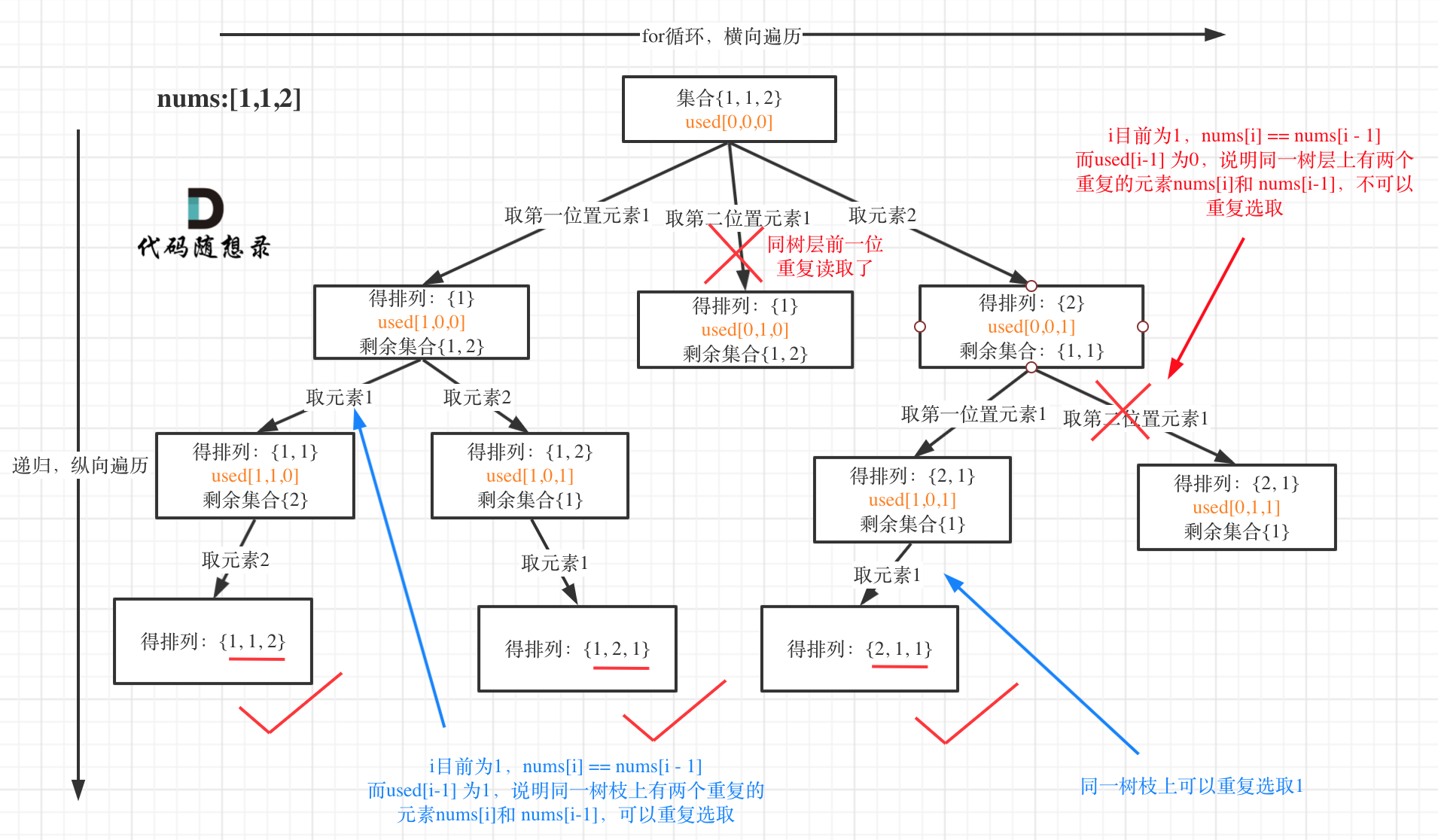
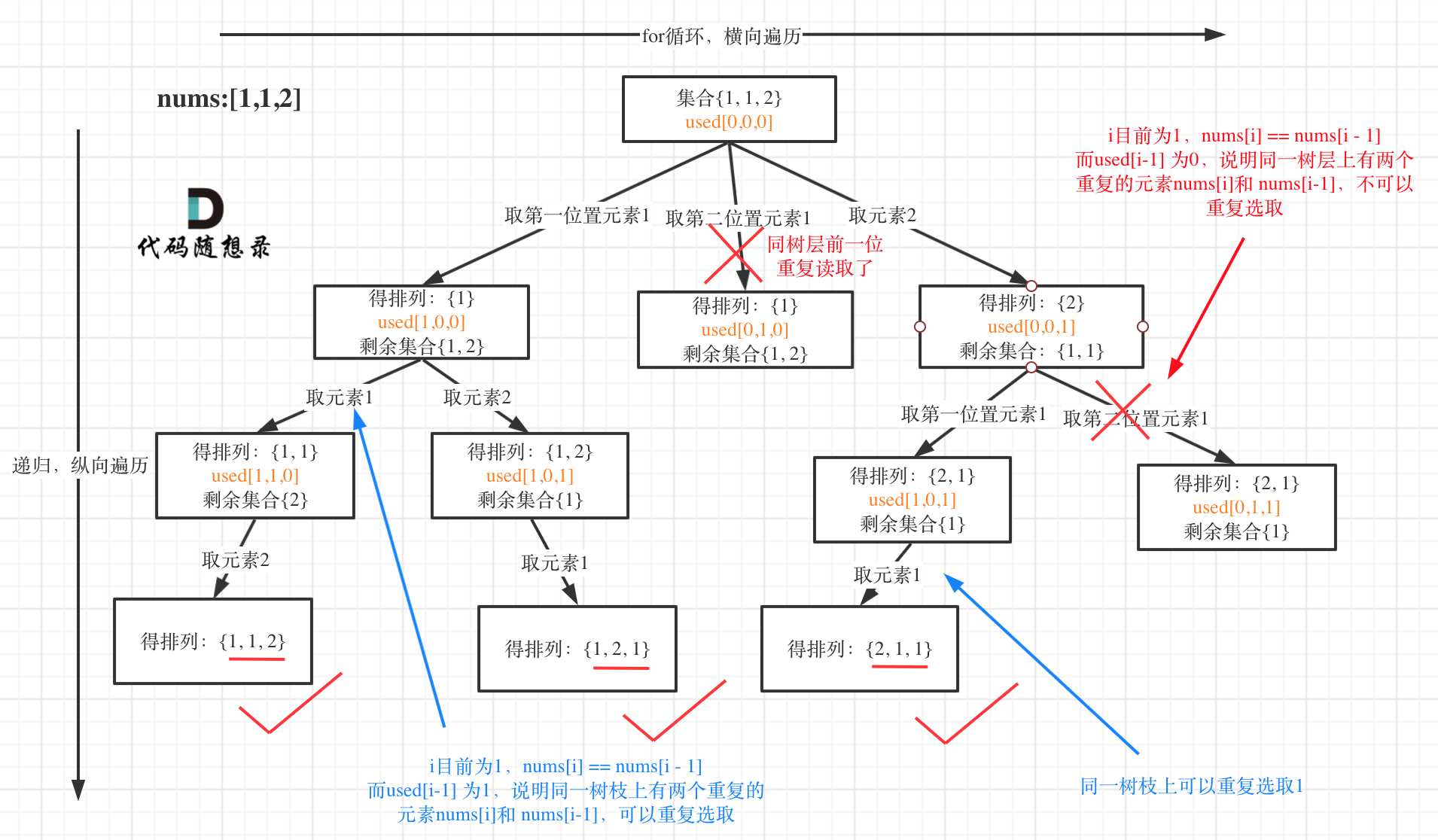
 树形结构如下：
 
-![47.全排列II1](https://img-blog.csdnimg.cn/20201112171930470.png)
+![47.全排列II1](https://code-thinking-1253855093.file.myqcloud.com/pics/20201112171930470-20230310133206398.png)
 
 **这道题目神奇的地方就是used[i - 1] == false也可以，used[i - 1] == true也可以！**
 
@@ -55,11 +54,11 @@
 
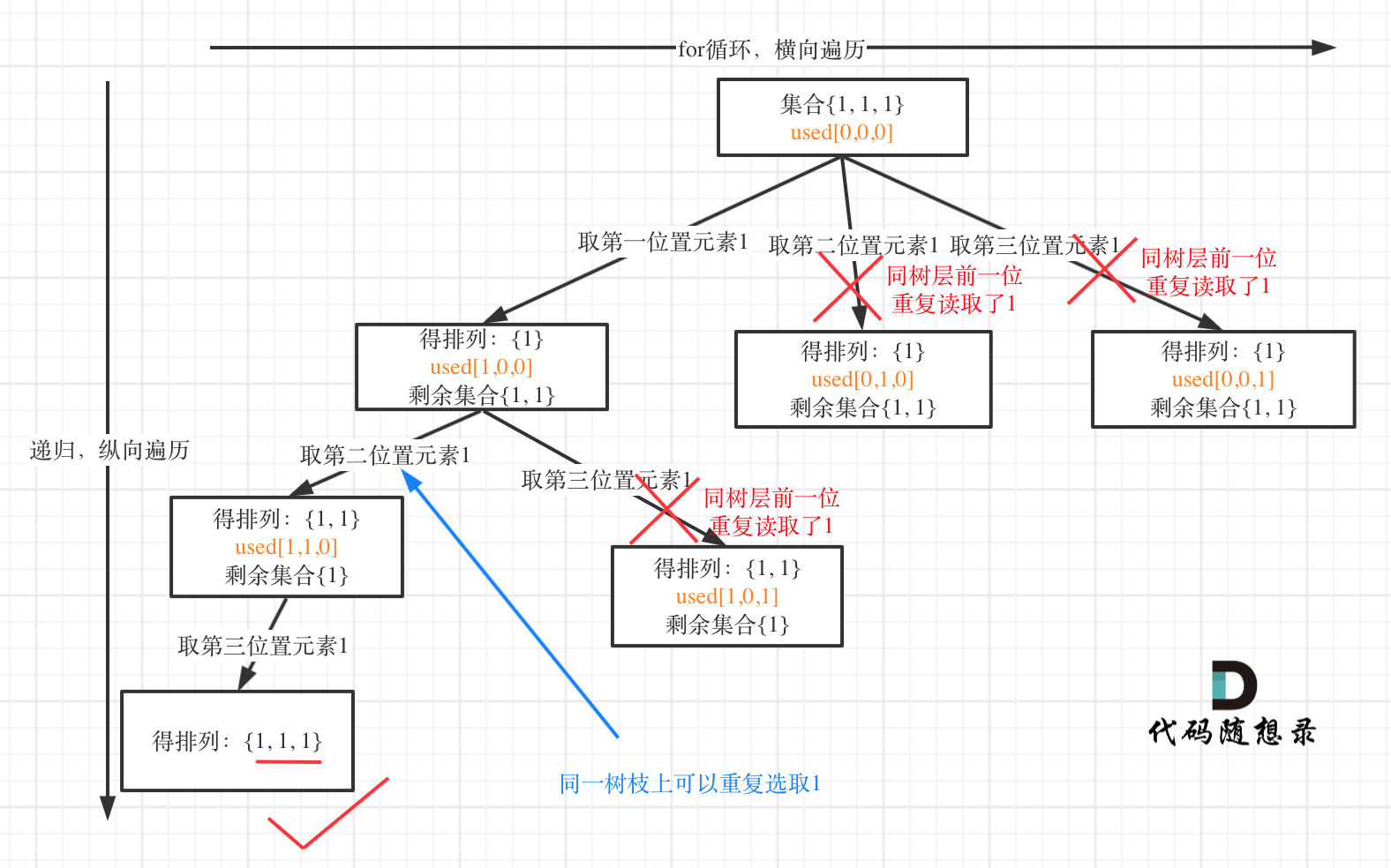
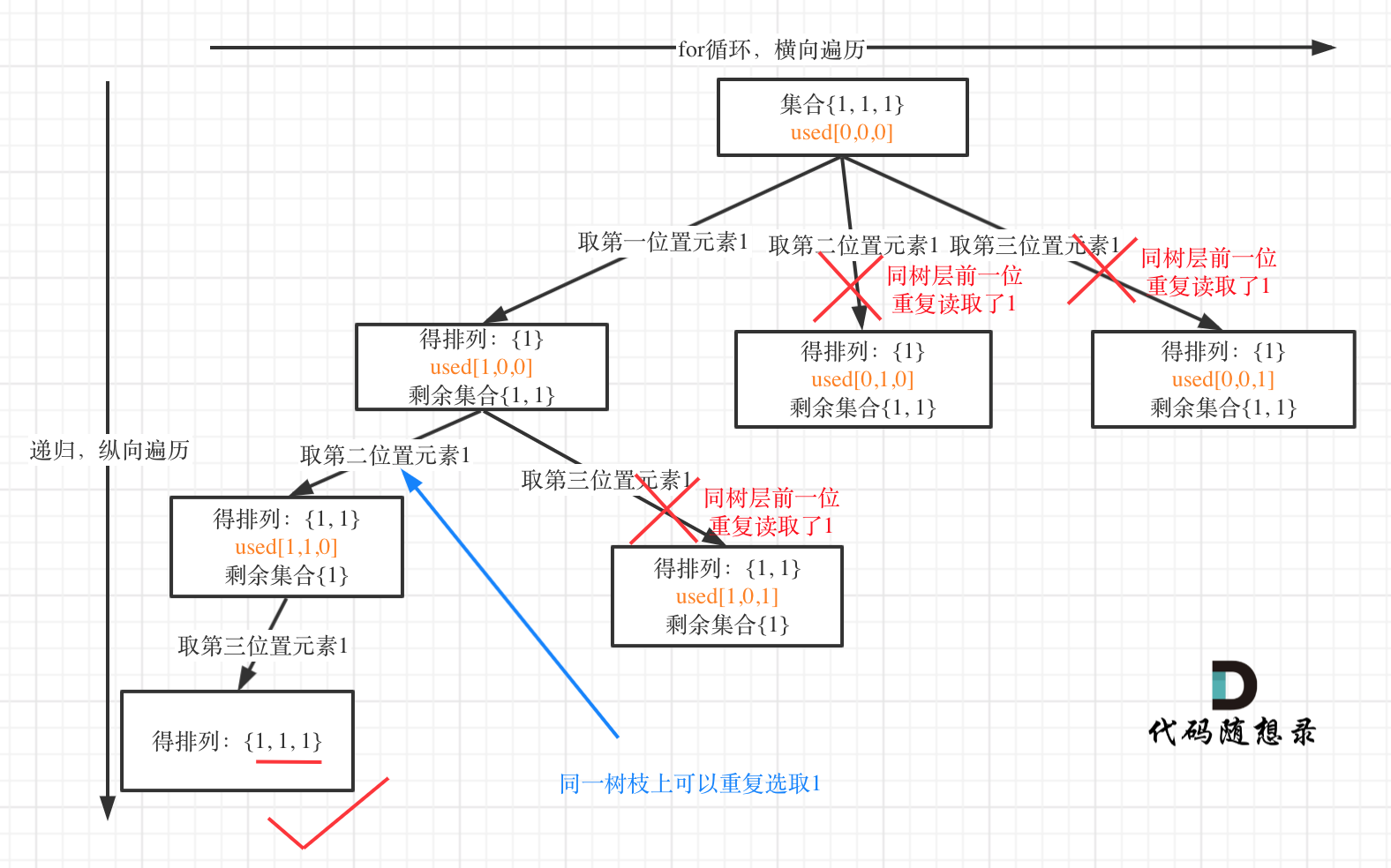
 树层上去重(used[i - 1] == false)，的树形结构如下：
 
-![47.全排列II2.png](https://img-blog.csdnimg.cn/20201112172230434.png)
+![47.全排列II2.png](https://code-thinking-1253855093.file.myqcloud.com/pics/20201112172230434-20230310133211392.png)
 
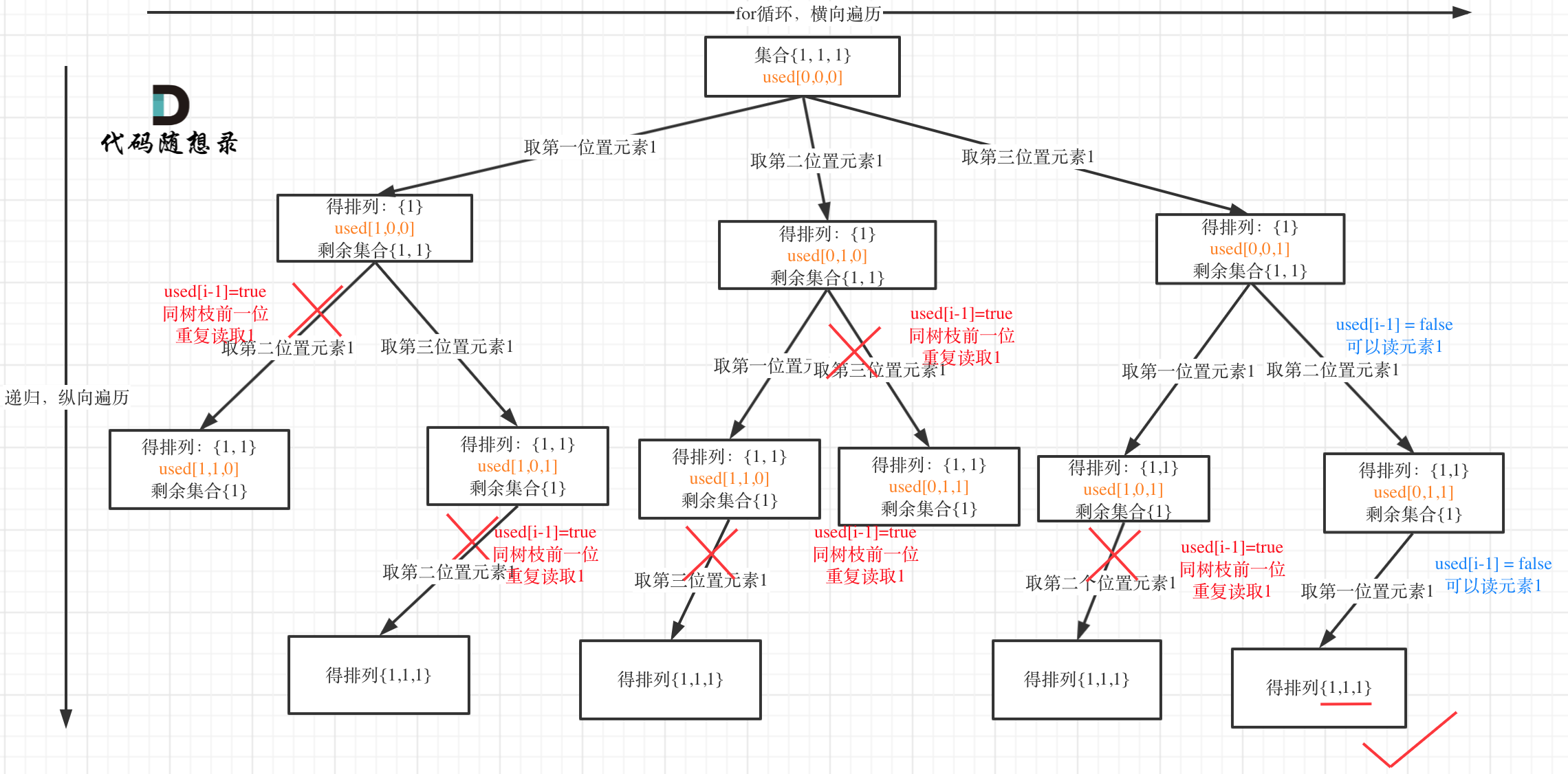
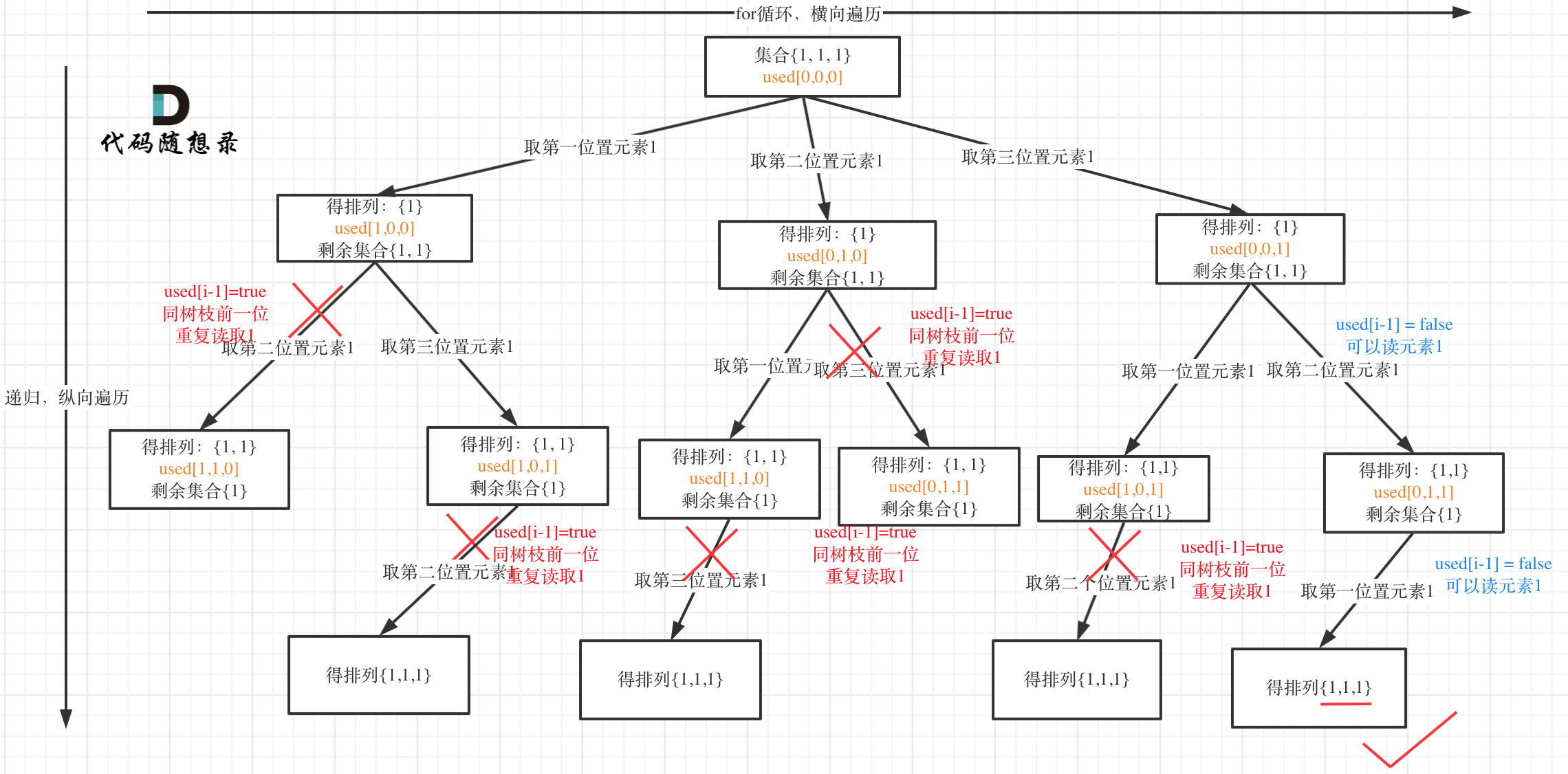
 树枝上去重（used[i - 1] == true）的树型结构如下：
 
-![47.全排列II3](https://img-blog.csdnimg.cn/20201112172327967.png)
+![47.全排列II3](https://code-thinking-1253855093.file.myqcloud.com/pics/20201112172327967-20230310133216389.png)
 
 **可以清晰的看到使用(used[i - 1] == false)，即树层去重，效率更高！**
 
@@ -72,14 +71,17 @@
 **所以这块就说一说我个人理解，对内容持开放态度，集思广益，欢迎大家来讨论！**
 
 子集问题分析：
+
 * 时间复杂度：$O(n × 2^n)$，因为每一个元素的状态无外乎取与不取，所以时间复杂度为$O(2^n)$，构造每一组子集都需要填进数组，又有需要$O(n)$，最终时间复杂度：$O(n × 2^n)$。
 * 空间复杂度：$O(n)$，递归深度为n，所以系统栈所用空间为$O(n)$，每一层递归所用的空间都是常数级别，注意代码里的result和path都是全局变量，就算是放在参数里，传的也是引用，并不会新申请内存空间，最终空间复杂度为$O(n)$。
 
 排列问题分析：
+
 * 时间复杂度：$O(n!)$，这个可以从排列的树形图中很明显发现，每一层节点为n，第二层每一个分支都延伸了n-1个分支，再往下又是n-2个分支，所以一直到叶子节点一共就是 n * n-1 * n-2 * ..... 1 = n!。每个叶子节点都会有一个构造全排列填进数组的操作（对应的代码：`result.push_back(path)`），该操作的复杂度为$O(n)$。所以，最终时间复杂度为：n * n!，简化为$O(n!)$。
 * 空间复杂度：$O(n)$，和子集问题同理。
 
 组合问题分析：
+
 * 时间复杂度：$O(n × 2^n)$，组合问题其实就是一种子集的问题，所以组合问题最坏的情况，也不会超过子集问题的时间复杂度。
 * 空间复杂度：$O(n)$，和子集问题同理。