CS_learn/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2026-02-02 18:39:09 +08:00
Code Issues Packages Projects Releases Wiki Activity

更新图床

Browse Source
This commit is contained in:
programmercarl
2023-03-10 14:02:32 +08:00
parent 2a9b627a90
commit 17cb4b45c7
134 changed files with 1169 additions and 829 deletions
Download Patch File Download Diff File Expand all files Collapse all files

10
problems/周总结/20210121动规周末总结.md
View File

@@ -1,4 +1,6 @@
# 本周小结！（动态规划系列三）
本周我们正式开始讲解背包问题，也是动规里非常重要的一类问题。
背包问题其实有很多细节，如果了解个大概，然后也能一气呵成把代码写出来，但稍稍变变花样可能会陷入迷茫了。
@@ -15,7 +17,7 @@
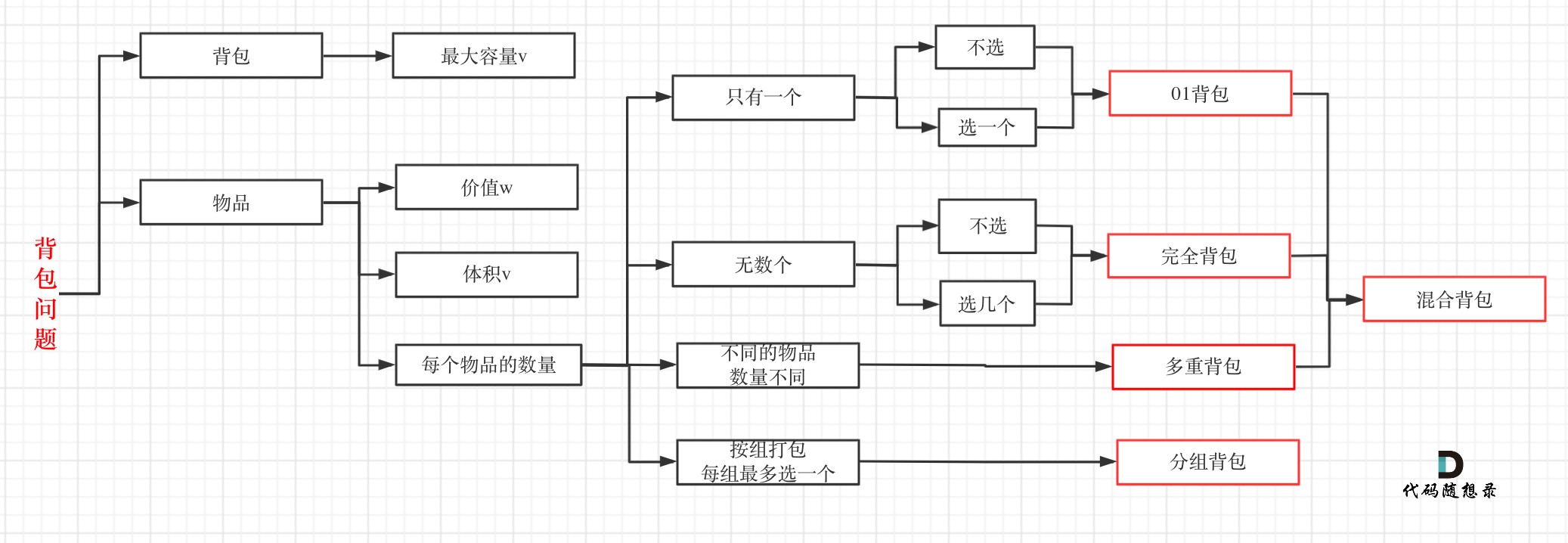
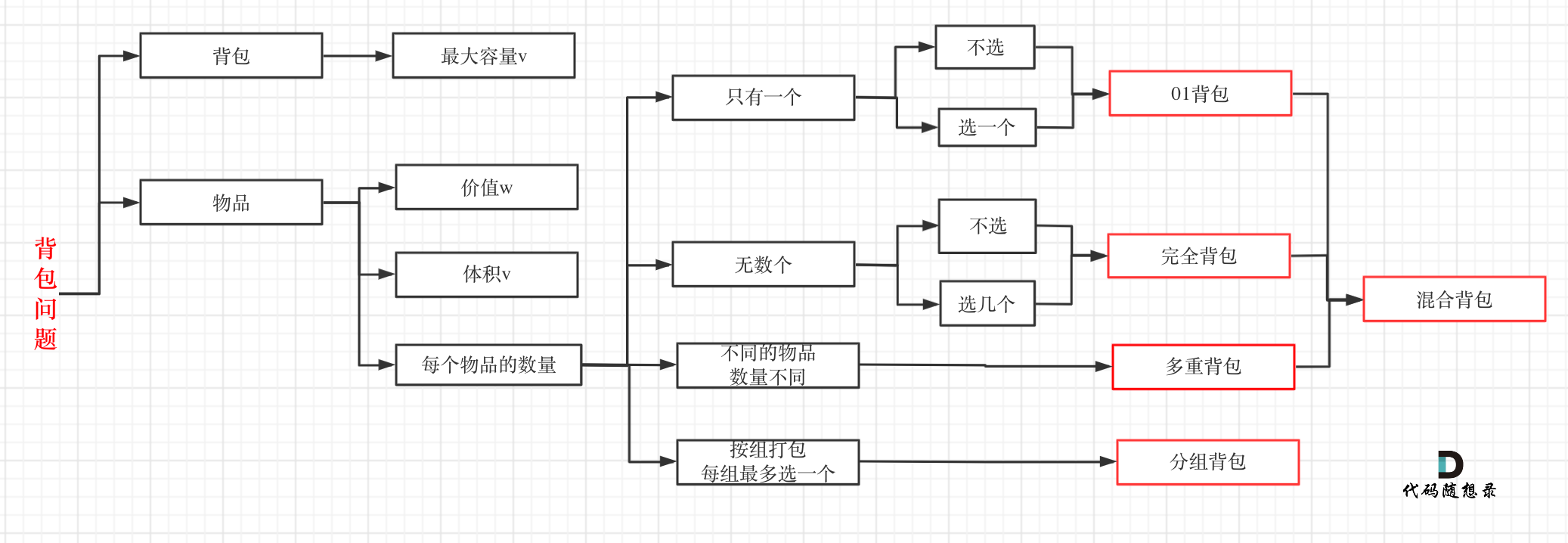
关于其他几种常用的背包，大家看这张图就了然于胸了：
![416.分割等和子集1](https://img-blog.csdnimg.cn/20210117171307407.png)
![416.分割等和子集1](https://code-thinking-1253855093.file.myqcloud.com/pics/20210117171307407-20230310133624872.png)
本文用动规五部曲详细讲解了01背包的二维dp数组的实现方法，大家其实可以发现最简单的是推导公式了，推导公式估计看一遍就记下来了，但难就难在确定初始化和遍历顺序上。
@@ -61,14 +63,14 @@ for(int i = 1; i < weight.size(); i++) { // 遍历物品
物品为：
| | 重量 | 价值 |
| --- | --- | --- |
| ----- | ---- | ---- |
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
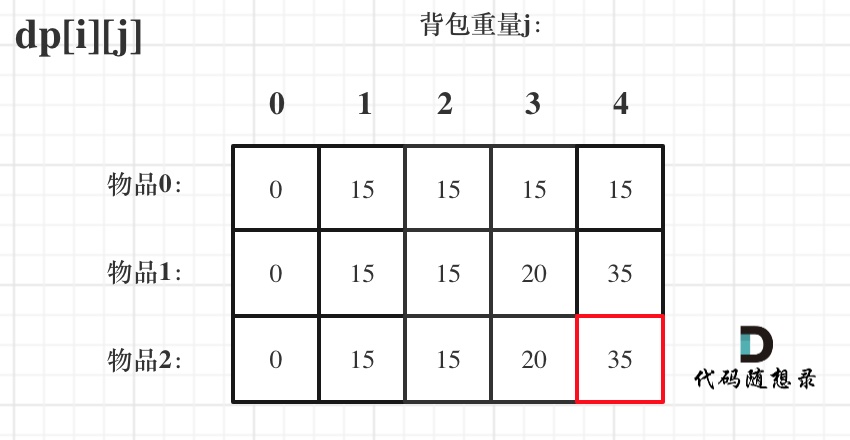
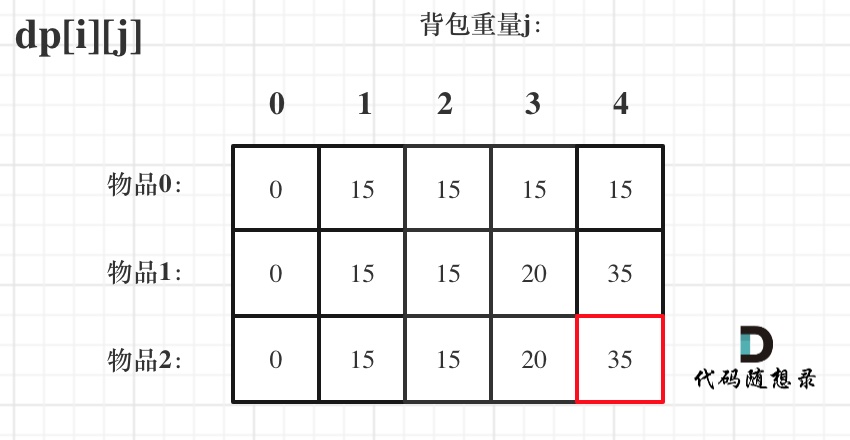
来看一下对应的dp数组的数值，如图：
![动态规划-背包问题4](https://img-blog.csdnimg.cn/20210118163425129.jpg)
![动态规划-背包问题4](https://code-thinking-1253855093.file.myqcloud.com/pics/20210118163425129-20230310133630224.jpg)
最终结果就是dp[2][4]。
@@ -120,7 +122,7 @@ for(int i = 0; i < weight.size(); i++) { // 遍历物品
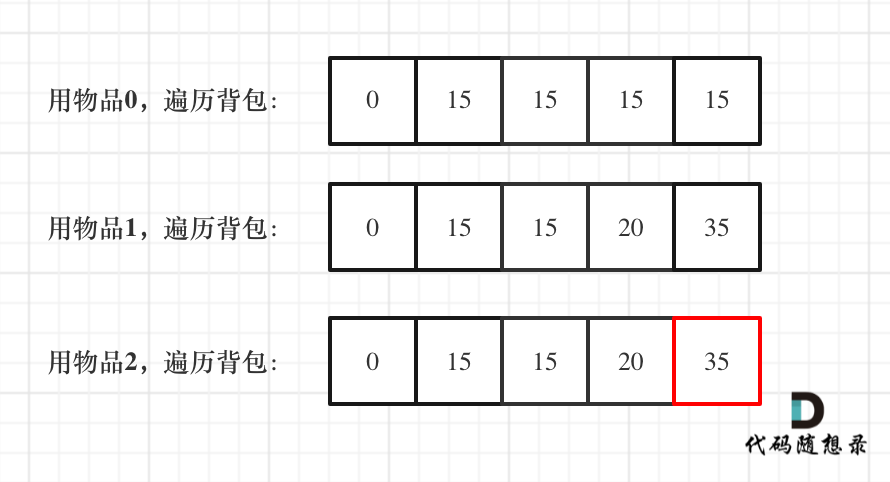
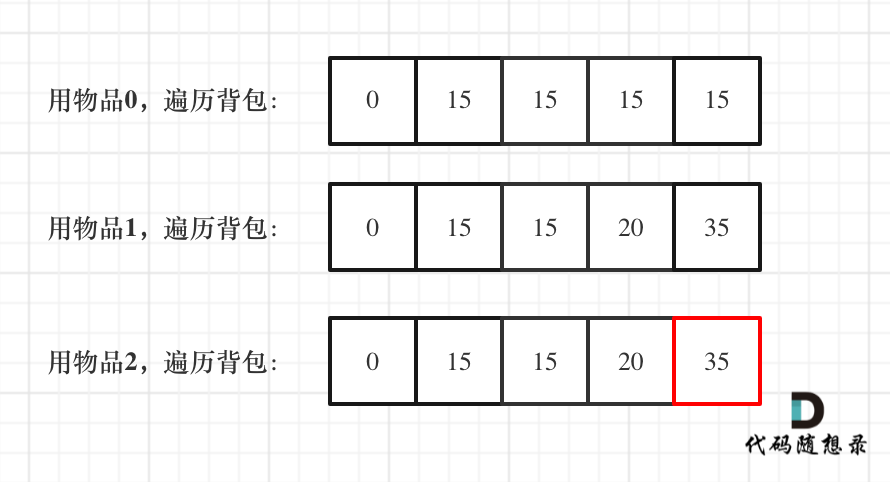
一维dp，分别用物品0，物品1，物品2 来遍历背包，最终得到结果如下：
![动态规划-背包问题9](https://img-blog.csdnimg.cn/20210110103614769.png)
![动态规划-背包问题9](https://code-thinking-1253855093.file.myqcloud.com/pics/20210110103614769-20230310133634873.png)
## 周三