CS_learn/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2026-02-02 18:39:09 +08:00
Code Issues Packages Projects Releases Wiki Activity

更新图床

Browse Source
This commit is contained in:
programmercarl
2023-03-10 14:02:32 +08:00
parent 2a9b627a90
commit 17cb4b45c7
134 changed files with 1169 additions and 829 deletions
Download Patch File Download Diff File Expand all files Collapse all files

84
problems/0106.从中序与后序遍历序列构造二叉树.md
View File

@@ -1,3 +1,4 @@
<p align="center">
<a href="https://programmercarl.com/other/xunlianying.html" target="_blank">
<img src="../pics/训练营.png" width="1000"/>
@@ -5,6 +6,7 @@
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>
看完本文，可以一起解决如下两道题目
* 106.从中序与后序遍历序列构造二叉树
@@ -21,11 +23,11 @@
例如，给出
* 中序遍历 inorder = [9,3,15,20,7]
* 中序遍历 inorder = [9,3,15,20,7]
* 后序遍历 postorder = [9,15,7,20,3]
返回如下的二叉树：
返回如下的二叉树：
![106. 从中序与后序遍历序列构造二叉树1](https://img-blog.csdnimg.cn/20210203154316774.png)
![106. 从中序与后序遍历序列构造二叉树1](https://code-thinking-1253855093.file.myqcloud.com/pics/20210203154316774.png)
# 视频讲解
@@ -40,7 +42,7 @@
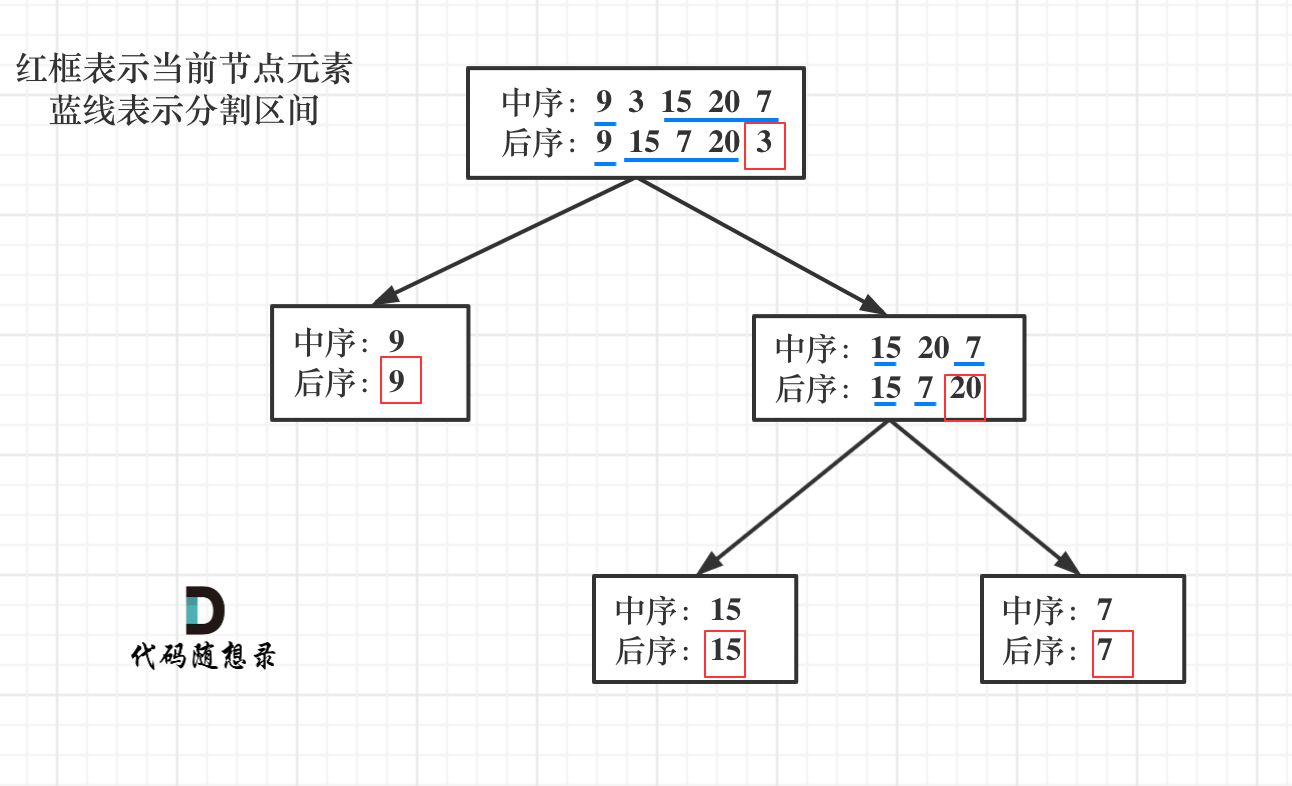
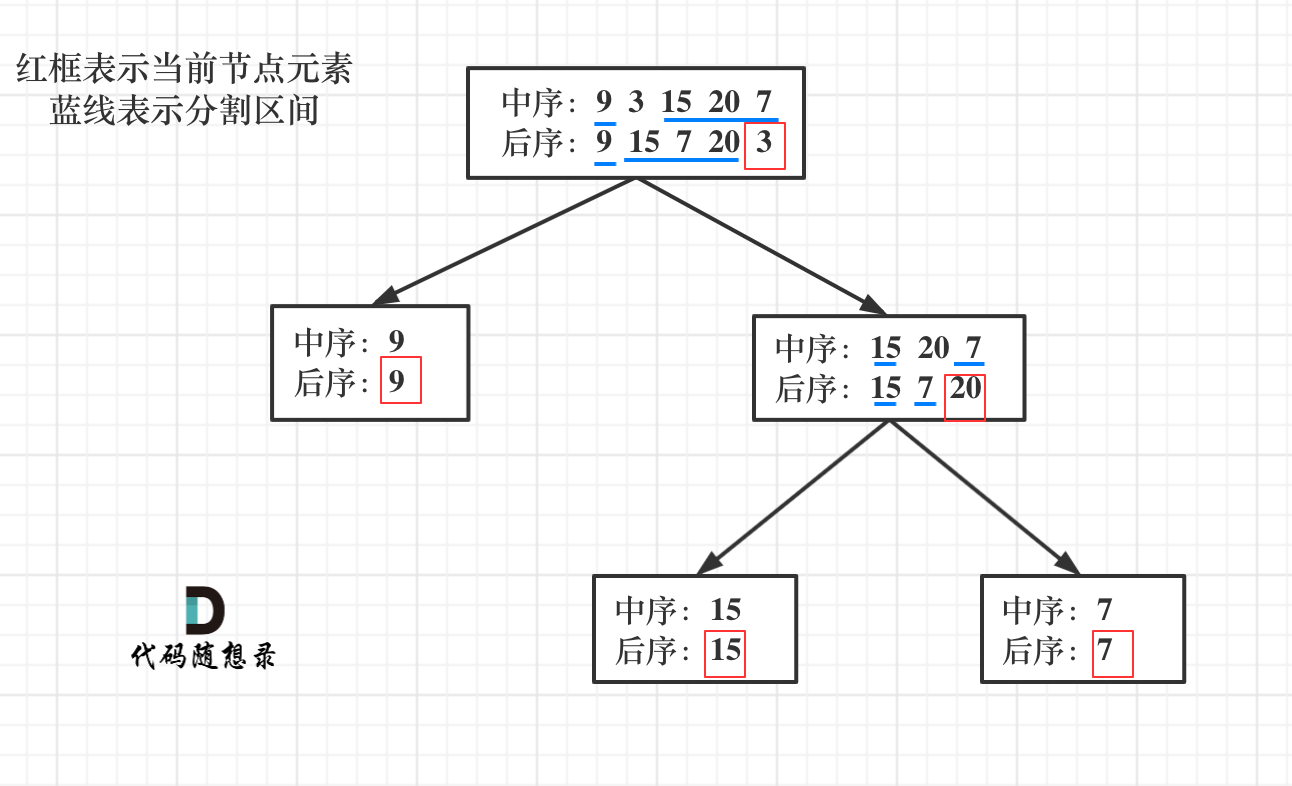
流程如图：
![106.从中序与后序遍历序列构造二叉树](https://img-blog.csdnimg.cn/20210203154249860.png)
![106.从中序与后序遍历序列构造二叉树](https://code-thinking-1253855093.file.myqcloud.com/pics/20210203154249860.png)
那么代码应该怎么写呢？
@@ -280,6 +282,7 @@ public:
下面给出用下标索引写出的代码版本：（思路是一样的，只不过不用重复定义vector了，每次用下标索引来分割）
### C++优化版本
```CPP
class Solution {
private:
@@ -397,7 +400,7 @@ public:
};
```
## Python
## Python
# 105.从前序与中序遍历序列构造二叉树
@@ -411,11 +414,11 @@ public:
例如，给出
前序遍历 preorder = [3,9,20,15,7]
前序遍历 preorder = [3,9,20,15,7]
中序遍历 inorder = [9,3,15,20,7]
返回如下的二叉树：
![105. 从前序与中序遍历序列构造二叉树](https://img-blog.csdnimg.cn/20210203154626672.png)
![105. 从前序与中序遍历序列构造二叉树](https://code-thinking-1253855093.file.myqcloud.com/pics/20210203154626672.png)
## 思路
@@ -558,7 +561,7 @@ public:
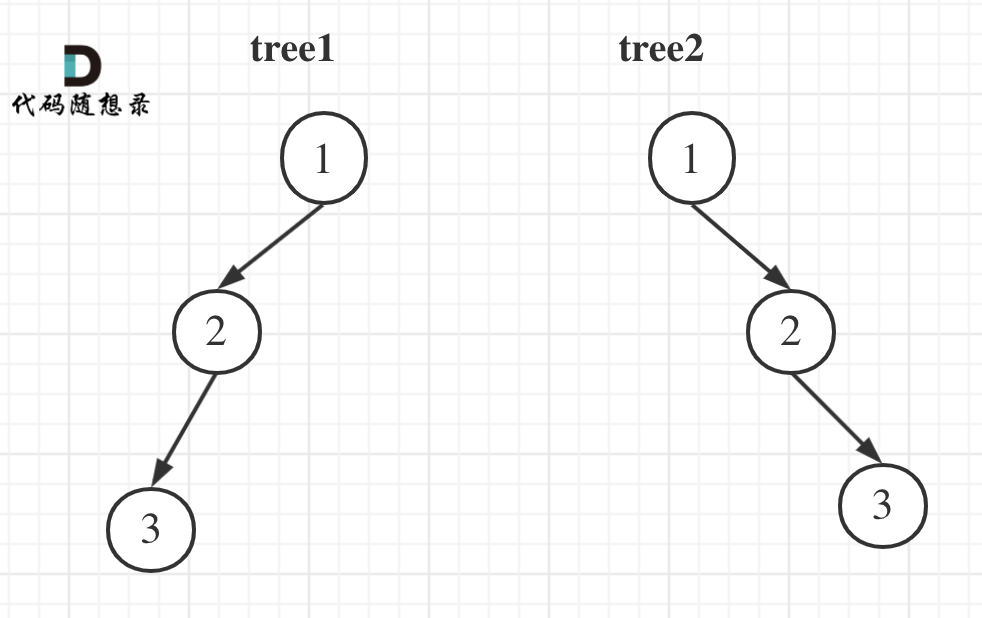
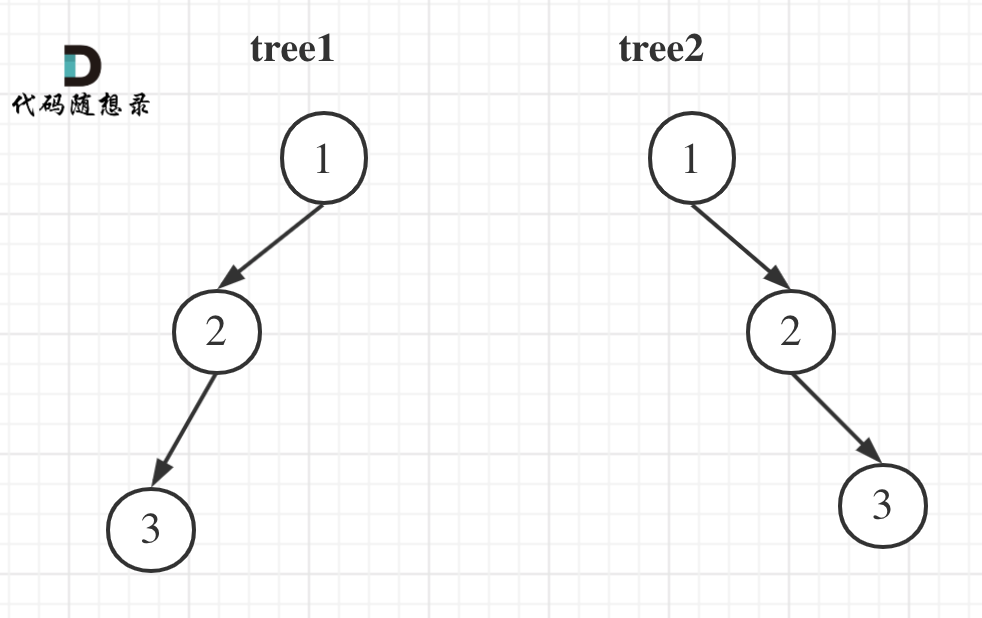
举一个例子：
![106.从中序与后序遍历序列构造二叉树2](https://img-blog.csdnimg.cn/20210203154720326.png)
![106.从中序与后序遍历序列构造二叉树2](https://code-thinking-1253855093.file.myqcloud.com/pics/20210203154720326.png)
tree1 的前序遍历是[1 2 3]， 后序遍历是[3 2 1]。
@@ -601,7 +604,7 @@ class Solution {
return findNode(inorder, 0, inorder.length, postorder,0, postorder.length); // 前闭后开
}
public TreeNode findNode(int[] inorder, int inBegin, int inEnd, int[] postorder, int postBegin, int postEnd) {
// 参数里的范围都是前闭后开
if (inBegin >= inEnd || postBegin >= postEnd) { // 不满足左闭右开，说明没有元素，返回空树
@@ -642,7 +645,7 @@ class Solution {
int rootIndex = map.get(preorder[preBegin]); // 找到前序遍历的第一个元素在中序遍历中的位置
TreeNode root = new TreeNode(inorder[rootIndex]); // 构造结点
int lenOfLeft = rootIndex - inBegin; // 保存中序左子树个数，用来确定前序数列的个数
root.left = findNode(preorder, preBegin + 1, preBegin + lenOfLeft + 1,
root.left = findNode(preorder, preBegin + 1, preBegin + lenOfLeft + 1,
inorder, inBegin, rootIndex);
root.right = findNode(preorder, preBegin + lenOfLeft + 1, preEnd,
inorder, rootIndex + 1, inEnd);
@@ -652,18 +655,19 @@ class Solution {
}
```
## Python
## Python
```python
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> Optional[TreeNode]:
# 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
if not postorder:
return
return
# 第二步: 后序遍历的最后一个就是当前的中间节点
root_val = postorder[-1]
root = TreeNode(root_val)
# 第三步: 找切割点.
root_index = inorder.index(root_val)
@@ -672,7 +676,7 @@ class Solution:
right_inorder = inorder[root_index + 1:]
# 第五步: 切割postorder数组. 得到postorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
left_postorder = postorder[:len(left_inorder)]
right_postorder = postorder[len(left_inorder): len(postorder) - 1]
@@ -682,7 +686,7 @@ class Solution:
root.right = self.buildTree(right_inorder, right_postorder)
# 第七步: 返回答案
return root
return root
```
105.从前序与中序遍历序列构造二叉树
@@ -691,22 +695,22 @@ class Solution:
class Solution:
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
if not preorder:
if not preorder:
return None
# 第二步: 前序遍历的第一个就是当前的中间节点.
# 第二步: 前序遍历的第一个就是当前的中间节点.
root_val = preorder[0]
root = TreeNode(root_val)
# 第三步: 找切割点.
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割preorder数组. 得到preorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟前序数组大小是相同的.
# ⭐️ 重点1: 中序数组大小一定跟前序数组大小是相同的.
preorder_left = preorder[1:1 + len(inorder_left)]
preorder_right = preorder[1 + len(inorder_left):]
@@ -723,22 +727,22 @@ class Solution:
class Solution:
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
# 第一步: 特殊情况讨论: 树为空. (递归终止条件)
if not postorder:
if not postorder:
return None
# 第二步: 后序遍历的最后一个就是当前的中间节点.
# 第二步: 后序遍历的最后一个就是当前的中间节点.
root_val = postorder[-1]
root = TreeNode(root_val)
# 第三步: 找切割点.
# 第三步: 找切割点.
separator_idx = inorder.index(root_val)
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
inorder_left = inorder[:separator_idx]
inorder_right = inorder[separator_idx + 1:]
# 第五步: 切割postorder数组. 得到postorder数组的左,右半边.
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
postorder_left = postorder[:len(inorder_left)]
postorder_right = postorder[len(inorder_left): len(postorder) - 1]
@@ -746,7 +750,7 @@ class Solution:
root.left = self.buildTree(inorder_left, postorder_left)
root.right = self.buildTree(inorder_right, postorder_right)
return root
return root
```
## Go
@@ -786,7 +790,7 @@ func rebuild(inorder []int, postorder []int, rootIdx int, l, r int) *TreeNode {
rootIn := hash[rootV] // 找到根节点在对应的中序数组中的位置
root := &TreeNode{Val : rootV} // 构造根节点
// 重建左节点和右节点
root.Left = rebuild(inorder, postorder, rootIdx-(r-rootIn)-1, l, rootIn-1)
root.Left = rebuild(inorder, postorder, rootIdx-(r-rootIn)-1, l, rootIn-1)
root.Right = rebuild(inorder, postorder, rootIdx-1, rootIn+1, r)
return root
}
@@ -830,7 +834,7 @@ func build(pre []int, in []int, root int, l, r int) *TreeNode {
## JavaScript
## JavaScript
```javascript
var buildTree = function(inorder, postorder) {
@@ -1031,7 +1035,7 @@ struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int in
// 4.根据中序遍历数组左右数组的各子大小切割前序遍历数组。也分为左右数组
int* leftPreorder = preorder+1;
int* rightPreorder = preorder + 1 + leftNum;
int* rightPreorder = preorder + 1 + leftNum;
// 5.递归进入左右数组，将返回的结果作为根结点的左右孩子
root->left = buildTree(leftPreorder, leftNum, leftInorder, leftNum);
@@ -1056,26 +1060,26 @@ class Solution {
inorderBegin: 0,
inorderEnd: inorder.count)
}
func helper(preorder: [Int], preorderBegin: Int, preorderEnd: Int, inorder: [Int], inorderBegin: Int, inorderEnd: Int) -> TreeNode? {
if preorderBegin == preorderEnd {
return nil
}
// 前序遍历数组的第一个元素作为分割点
let rootValue = preorder[preorderBegin]
let root = TreeNode(rootValue)
if preorderEnd - preorderBegin == 1 {
return root
}
var index = 0 // 从中序遍历数组中找到根节点的下标
if let ind = inorder.firstIndex(of: rootValue) {
index = ind
}
// 递归
root.left = helper(preorder: preorder,
preorderBegin: preorderBegin + 1,
@@ -1102,28 +1106,28 @@ class Solution_0106 {
if postorderEnd - postorderBegin < 1 {
return nil
}
// 后序遍历数组的最后一个元素作为分割点
let rootValue = postorder[postorderEnd - 1]
let root = TreeNode(rootValue)
if postorderEnd - postorderBegin == 1 {
return root
}
// 从中序遍历数组中找到根节点的下标
var delimiterIndex = 0
if let index = inorder.firstIndex(of: rootValue) {
delimiterIndex = index
}
root.left = buildTree(inorder: inorder,
inorderBegin: inorderBegin,
inorderEnd: delimiterIndex,
postorder: postorder,
postorderBegin: postorderBegin,
postorderEnd: postorderBegin + (delimiterIndex - inorderBegin))
root.right = buildTree(inorder: inorder,
inorderBegin: delimiterIndex + 1,
inorderEnd: inorderEnd,