- 
- 
+ 
+ 
- 
- 
+ 
-
+
+ 
+
-# 算法面试思维导图
-
-
-
-# B站算法视频讲解
-
-以下为[B站「代码随想录」](https://space.bilibili.com/525438321)算法讲解视频：
-
-* [帮你把KMP算法学个通透！（理论篇）](https://www.bilibili.com/video/BV1PD4y1o7nd)
-* [帮你把KMP算法学个通透！（代码篇）](https://www.bilibili.com/video/BV1M5411j7Xx)
-* [带你学透回溯算法（理论篇）](https://www.bilibili.com/video/BV1cy4y167mM)
-* [回溯算法之组合问题（力扣题目：77.组合）](https://www.bilibili.com/video/BV1ti4y1L7cv)
-* [组合问题的剪枝操作（对应力扣题目：77.组合）](https://www.bilibili.com/video/BV1wi4y157er)
-* [组合总和（对应力扣题目：39.组合总和）](https://www.bilibili.com/video/BV1KT4y1M7HJ/)
-
-（持续更新中....）
# LeetCode 刷题攻略
@@ -43,191 +30,224 @@
很多刚开始刷题的同学都有一个困惑：面对leetcode上近两千道题目，从何刷起。
+大家平时刷题感觉效率低，浪费的时间主要在三点：
+
+* 找题
+* 找到了不应该现阶段做的题
+* 没有全套的优质题解可以参考
+
其实我之前在知乎上回答过这个问题，回答内容大概是按照如下类型来刷数组-> 链表-> 哈希表->字符串->栈与队列->树->回溯->贪心->动态规划->图论->高级数据结构，再从简单刷起，做了几个类型题目之后，再慢慢做中等题目、困难题目。
但我能设身处地的感受到：即使有这样一个整体规划，对于一位初学者甚至算法老手寻找合适自己的题目也是很困难，时间成本很高，而且题目还不一定就是经典题目。
-对于刷题，我们都是想用最短的时间把经典题目都做一篇，这样效率才是最高的！
+对于刷题，我们都是想用最短的时间**按照循序渐进的难度顺序把经典题目都做一遍**，这样效率才是最高的！
-所以我整理了leetcode刷题攻略：一个超级详细的刷题顺序，**每道题目都是我精心筛选，都是经典题目高频面试题**，大家只要按照这个顺序刷就可以了，**你没看错，就是题目顺序都排好了，文章顺序就是刷题顺序！挨个刷就可以，不用自己再去题海里选题了！**
+所以我整理了leetcode刷题攻略：一个超级详细的刷题顺序，**每道题目都是我精心筛选，都是经典题目高频面试题**，大家只要按照这个顺序刷就可以了，**你没看错，README已经把题目顺序都排好了，文章顺序就是刷题顺序！挨个刷就可以，不用自己再去题海里选题了！**
而且每道题目我都写了的详细题解（图文并茂，难点配有视频），力扣上我的题解都是排在对应题目的首页，质量是有目共睹的。
-**那么今天我把这个刷题顺序整理出来，是为了帮助更多的学习算法的同学少走弯路！**
+**那么现在我把刷题顺序都整理出来，是为了帮助更多的学习算法的同学少走弯路！**
如果你在刷leetcode，强烈建议先按照本攻略刷题顺序来刷，刷完了你会发现对整个知识体系有一个质的飞跃，不用在题海茫然的寻找方向。
-**文章会首发在公众号[「代码随想录」](https://img-blog.csdnimg.cn/20201124161234338.png)，赶紧去看看吧，你一定会发现相见恨晚！**
+
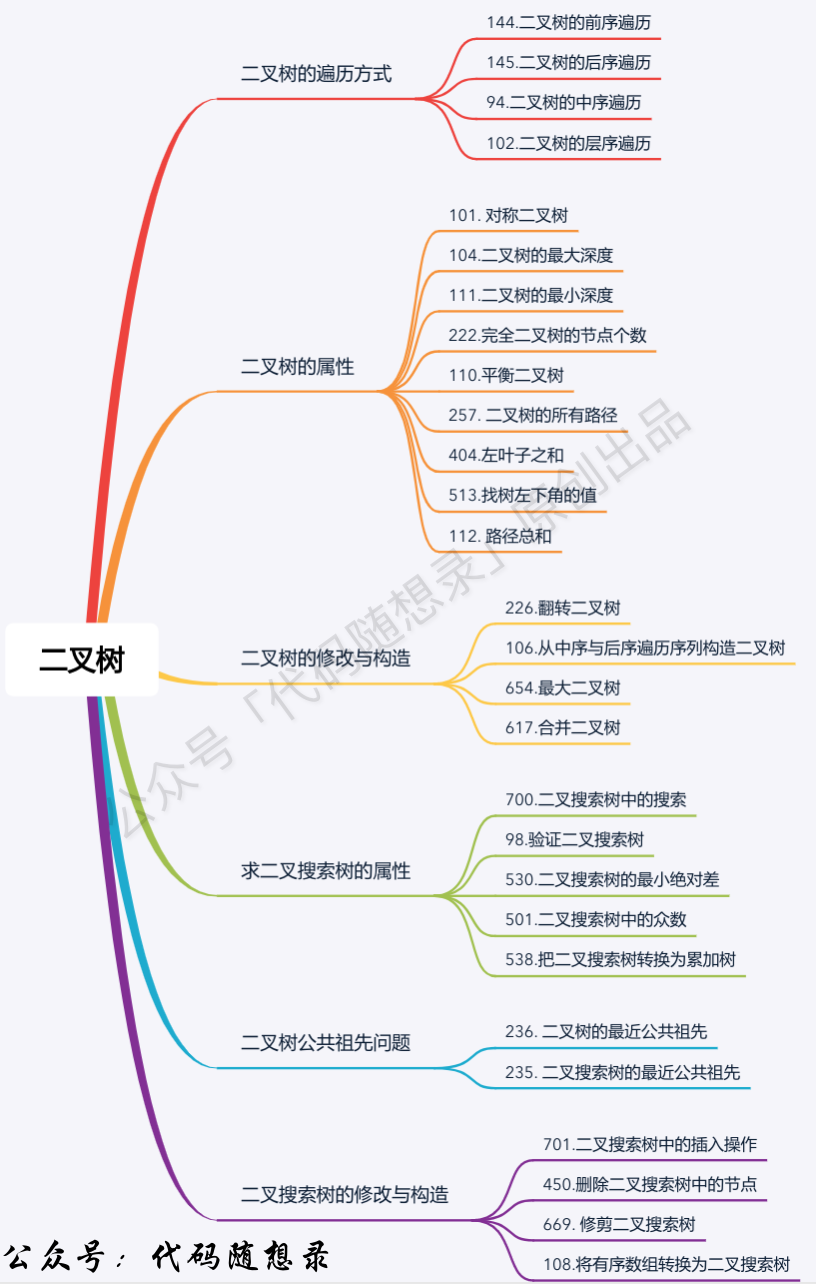-1. [关于二叉树，你该了解这些！](https://mp.weixin.qq.com/s/_ymfWYvTNd2GvWvC5HOE4A)
-2. [二叉树：一入递归深似海，从此offer是路人](https://mp.weixin.qq.com/s/PwVIfxDlT3kRgMASWAMGhA)
-3. [二叉树：听说递归能做的，栈也能做！](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg)
-4. [二叉树：前中后序迭代方式的写法就不能统一一下么？](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)
-5. [二叉树：层序遍历登场！](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
-6. [二叉树：你真的会翻转二叉树么？](https://mp.weixin.qq.com/s/6gY1MiXrnm-khAAJiIb5Bg)
-7. [本周小结！（二叉树）](https://mp.weixin.qq.com/s/JWmTeC7aKbBfGx4TY6uwuQ)
-8. [二叉树：我对称么？](https://mp.weixin.qq.com/s/Kgf0gjvlDlNDfKIH2b1Oxg)
-9. [二叉树：看看这些树的最大深度](https://mp.weixin.qq.com/s/guKwV-gSNbA1CcbvkMtHBg)
-10. [二叉树：看看这些树的最小深度](https://mp.weixin.qq.com/s/BH8-gPC3_QlqICDg7rGSGA)
-11. [二叉树：我有多少个节点？](https://mp.weixin.qq.com/s/2_eAjzw-D0va9y4RJgSmXw)
-12. [二叉树：我平衡么？](https://mp.weixin.qq.com/s/isUS-0HDYknmC0Rr4R8mww)
-13. [二叉树：找我的所有路径？](https://mp.weixin.qq.com/s/Osw4LQD2xVUnCJ-9jrYxJA)
-14. [还在玩耍的你，该总结啦！（本周小结之二叉树）](https://mp.weixin.qq.com/s/QMBUTYnoaNfsVHlUADEzKg)
-15. [二叉树：以为使用了递归，其实还隐藏着回溯](https://mp.weixin.qq.com/s/ivLkHzWdhjQQD1rQWe6zWA)
-16. [二叉树：做了这么多题目了，我的左叶子之和是多少？](https://mp.weixin.qq.com/s/gBAgmmFielojU5Wx3wqFTA)
-17. [二叉树：我的左下角的值是多少？](https://mp.weixin.qq.com/s/MH2gbLvzQ91jHPKqiub0Nw)
-18. [二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？](https://mp.weixin.qq.com/s/6TWAVjxQ34kVqROWgcRFOg)
-19. [二叉树：构造二叉树登场！](https://mp.weixin.qq.com/s/7r66ap2s-shvVvlZxo59xg)
-20. [二叉树：构造一棵最大的二叉树](https://mp.weixin.qq.com/s/1iWJV6Aov23A7xCF4nV88w)
-21. [本周小结！（二叉树系列三）](https://mp.weixin.qq.com/s/JLLpx3a_8jurXcz6ovgxtg)
-22. [二叉树：合并两个二叉树](https://mp.weixin.qq.com/s/3f5fbjOFaOX_4MXzZ97LsQ)
-23. [二叉树：二叉搜索树登场！](https://mp.weixin.qq.com/s/vsKrWRlETxCVsiRr8v_hHg)
-24. [二叉树：我是不是一棵二叉搜索树](https://mp.weixin.qq.com/s/8odY9iUX5eSi0eRFSXFD4Q)
-25. [二叉树：搜索树的最小绝对差](https://mp.weixin.qq.com/s/Hwzml6698uP3qQCC1ctUQQ)
-26. [二叉树：我的众数是多少？](https://mp.weixin.qq.com/s/KSAr6OVQIMC-uZ8MEAnGHg)
-27. [二叉树：公共祖先问题](https://mp.weixin.qq.com/s/n6Rk3nc_X3TSkhXHrVmBTQ)
-28. [本周小结！（二叉树系列四）](https://mp.weixin.qq.com/s/CbdtOTP0N-HIP7DR203tSg)
-29. [二叉树：搜索树的公共祖先问题](https://mp.weixin.qq.com/s/Ja9dVw2QhBcg_vV-1fkiCg)
-30. [二叉树：搜索树中的插入操作](https://mp.weixin.qq.com/s/lwKkLQcfbCNX2W-5SOeZEA)
-31. [二叉树：搜索树中的删除操作](https://mp.weixin.qq.com/s/-p-Txvch1FFk3ygKLjPAKw)
-32. [二叉树：修剪一棵搜索树](https://mp.weixin.qq.com/s/QzmGfYUMUWGkbRj7-ozHoQ)
-33. [二叉树：构造一棵搜索树](https://mp.weixin.qq.com/s/sy3ygnouaZVJs8lhFgl9mw)
-34. [二叉树：搜索树转成累加树](https://mp.weixin.qq.com/s/hZtJh4T5lIGBarY-lZJf6Q)
-35. [二叉树：总结篇！（需要掌握的二叉树技能都在这里了）](https://mp.weixin.qq.com/s/-ZJn3jJVdF683ap90yIj4Q)
+1. [关于二叉树，你该了解这些！](./problems/二叉树理论基础.md)
+2. [二叉树：一入递归深似海，从此offer是路人](./problems/二叉树的递归遍历.md)
+3. [二叉树：听说递归能做的，栈也能做！](./problems/二叉树的迭代遍历.md)
+4. [二叉树：前中后序迭代方式的写法就不能统一一下么？](./problems/二叉树的统一迭代法.md)
+5. [二叉树：层序遍历登场！](./problems/0102.二叉树的层序遍历.md)
+6. [二叉树：你真的会翻转二叉树么？](./problems/0226.翻转二叉树.md)
+7. [本周小结！（二叉树）](./problems/周总结/20200927二叉树周末总结.md)
+8. [二叉树：我对称么？](./problems/0101.对称二叉树.md)
+9. [二叉树：看看这些树的最大深度](./problems/0104.二叉树的最大深度.md)
+10. [二叉树：看看这些树的最小深度](./problems/0111.二叉树的最小深度.md)
+11. [二叉树：我有多少个节点？](./problems/0222.完全二叉树的节点个数.md)
+12. [二叉树：我平衡么？](./problems/0110.平衡二叉树.md)
+13. [二叉树：找我的所有路径？](./problems/0257.二叉树的所有路径.md)
+14. [本周总结！二叉树系列二](./problems/周总结/20201003二叉树周末总结.md)
+15. [二叉树：以为使用了递归，其实还隐藏着回溯](./problems/二叉树中递归带着回溯.md)
+16. [二叉树：做了这么多题目了，我的左叶子之和是多少？](./problems/0404.左叶子之和.md)
+17. [二叉树：我的左下角的值是多少？](./problems/0513.找树左下角的值.md)
+18. [二叉树：递归函数究竟什么时候需要返回值，什么时候不要返回值？](./problems/0112.路径总和.md)
+19. [二叉树：构造二叉树登场！](./problems/0106.从中序与后序遍历序列构造二叉树.md)
+20. [二叉树：构造一棵最大的二叉树](./problems/0654.最大二叉树.md)
+21. [本周小结！（二叉树系列三）](./problems/周总结/20201010二叉树周末总结.md)
+22. [二叉树：合并两个二叉树](./problems/0617.合并二叉树.md)
+23. [二叉树：二叉搜索树登场！](./problems/0700.二叉搜索树中的搜索.md)
+24. [二叉树：我是不是一棵二叉搜索树](./problems/0098.验证二叉搜索树.md)
+25. [二叉树：搜索树的最小绝对差](./problems/0530.二叉搜索树的最小绝对差.md)
+26. [二叉树：我的众数是多少？](./problems/0501.二叉搜索树中的众数.md)
+27. [二叉树：公共祖先问题](./problems/0236.二叉树的最近公共祖先.md)
+28. [本周小结！（二叉树系列四）](./problems/周总结/20201017二叉树周末总结.md)
+29. [二叉树：搜索树的公共祖先问题](./problems/0235.二叉搜索树的最近公共祖先.md)
+30. [二叉树：搜索树中的插入操作](./problems/0701.二叉搜索树中的插入操作.md)
+31. [二叉树：搜索树中的删除操作](./problems/0450.删除二叉搜索树中的节点.md)
+32. [二叉树：修剪一棵搜索树](./problems/0669.修剪二叉搜索树.md)
+33. [二叉树：构造一棵搜索树](./problems/0108.将有序数组转换为二叉搜索树.md)
+34. [二叉树：搜索树转成累加树](./problems/0538.把二叉搜索树转换为累加树.md)
+35. [二叉树：总结篇！（需要掌握的二叉树技能都在这里了）](./problems/二叉树总结篇.md)
## 回溯算法
@@ -235,32 +255,28 @@
-1. [关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw)
-2. [回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)
-3. [回溯算法：组合问题再剪剪枝](https://mp.weixin.qq.com/s/Ri7spcJMUmph4c6XjPWXQA)
-4. [回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)
-5. [回溯算法：电话号码的字母组合](https://mp.weixin.qq.com/s/e2ua2cmkE_vpYjM3j6HY0A)
-6. [本周小结！（回溯算法系列一）](https://mp.weixin.qq.com/s/m2GnTJdkYhAamustbb6lmw)
-7. [回溯算法：求组合总和（二）](https://mp.weixin.qq.com/s/FLg8G6EjVcxBjwCbzpACPw)
-8. [回溯算法：求组合总和（三）](https://mp.weixin.qq.com/s/_1zPYk70NvHsdY8UWVGXmQ)
-9. [回溯算法：分割回文串](https://mp.weixin.qq.com/s/Pb1epUTbU8fHIht-g_MS5Q)
-10. [回溯算法：复原IP地址](https://mp.weixin.qq.com/s/v--VmA8tp9vs4bXCqHhBuA)
-11. [回溯算法：求子集问题！](https://mp.weixin.qq.com/s/NNRzX-vJ_pjK4qxohd_LtA)
-12. [本周小结！（回溯算法系列二）](https://mp.weixin.qq.com/s/uzDpjrrMCO8DOf-Tl5oBGw)
-13. [回溯算法：求子集问题（二）](https://mp.weixin.qq.com/s/WJ4JNDRJgsW3eUN72Hh3uQ)
-14. [回溯算法：递增子序列](https://mp.weixin.qq.com/s/ePxOtX1ATRYJb2Jq7urzHQ)
-15. [回溯算法：排列问题！](https://mp.weixin.qq.com/s/SCOjeMX1t41wcvJq49GhMw)
-16. [回溯算法：排列问题（二）](https://mp.weixin.qq.com/s/9L8h3WqRP_h8LLWNT34YlA)
-17. [本周小结！（回溯算法系列三）](https://mp.weixin.qq.com/s/tLkt9PSo42X60w8i94ViiA)
-18. [本周小结！（回溯算法系列三）续集](https://mp.weixin.qq.com/s/kSMGHc_YpsqL2j-jb_E_Ag)
-19. [视频来了！！带你学透回溯算法（理论篇）](https://www.bilibili.com/video/BV1cy4y167mM)
-20. [视频来了！！回溯算法（力扣题目：77.组合）](https://www.bilibili.com/video/BV1ti4y1L7cv)
-21. [视频来了！！回溯算法剪枝操作（力扣题目：77.组合）](https://www.bilibili.com/video/BV1wi4y157er)
-22. [视频来了！！回溯算法（力扣题目：39.组合总和）](https://www.bilibili.com/video/BV1KT4y1M7HJ/)
-23. [回溯算法：重新安排行程](https://mp.weixin.qq.com/s/3kmbS4qDsa6bkyxR92XCTA)
-24. [回溯算法：N皇后问题](https://mp.weixin.qq.com/s/lU_QwCMj6g60nh8m98GAWg)
-25. [回溯算法：解数独](https://mp.weixin.qq.com/s/eWE9TapVwm77yW9Q81xSZQ)
-26. [一篇总结带你彻底搞透回溯算法！](https://mp.weixin.qq.com/s/r73thpBnK1tXndFDtlsdCQ)
+1. [关于回溯算法，你该了解这些！](./problems/回溯算法理论基础.md)
+2. [回溯算法：组合问题](./problems/0077.组合.md)
+3. [回溯算法：组合问题再剪剪枝](./problems/0077.组合优化.md)
+4. [回溯算法：求组合总和！](./problems/0216.组合总和III.md)
+5. [回溯算法：电话号码的字母组合](./problems/0017.电话号码的字母组合.md)
+6. [本周小结！（回溯算法系列一）](./problems/周总结/20201030回溯周末总结.md)
+7. [回溯算法：求组合总和（二）](./problems/0039.组合总和.md)
+8. [回溯算法：求组合总和（三）](./problems/0040.组合总和II.md)
+9. [回溯算法：分割回文串](./problems/0131.分割回文串.md)
+10. [回溯算法：复原IP地址](./problems/0093.复原IP地址.md)
+11. [回溯算法：求子集问题！](./problems/0078.子集.md)
+12. [本周小结！（回溯算法系列二）](./problems/周总结/20201107回溯周末总结.md)
+13. [回溯算法：求子集问题（二）](./problems/0090.子集II.md)
+14. [回溯算法：递增子序列](./problems/0491.递增子序列.md)
+15. [回溯算法：排列问题！](./problems/0046.全排列.md)
+16. [回溯算法：排列问题（二）](./problems/0047.全排列II.md)
+17. [本周小结！（回溯算法系列三）](./problems/周总结/20201112回溯周末总结.md)
+18. [回溯算法去重问题的另一种写法](./problems/回溯算法去重问题的另一种写法.md)
+23. [回溯算法：重新安排行程](./problems/0332.重新安排行程.md)
+24. [回溯算法：N皇后问题](./problems/0051.N皇后.md)
+25. [回溯算法：解数独](./problems/0037.解数独.md)
+26. [一篇总结带你彻底搞透回溯算法！](./problems/回溯总结.md)
## 贪心算法
@@ -268,108 +284,119 @@
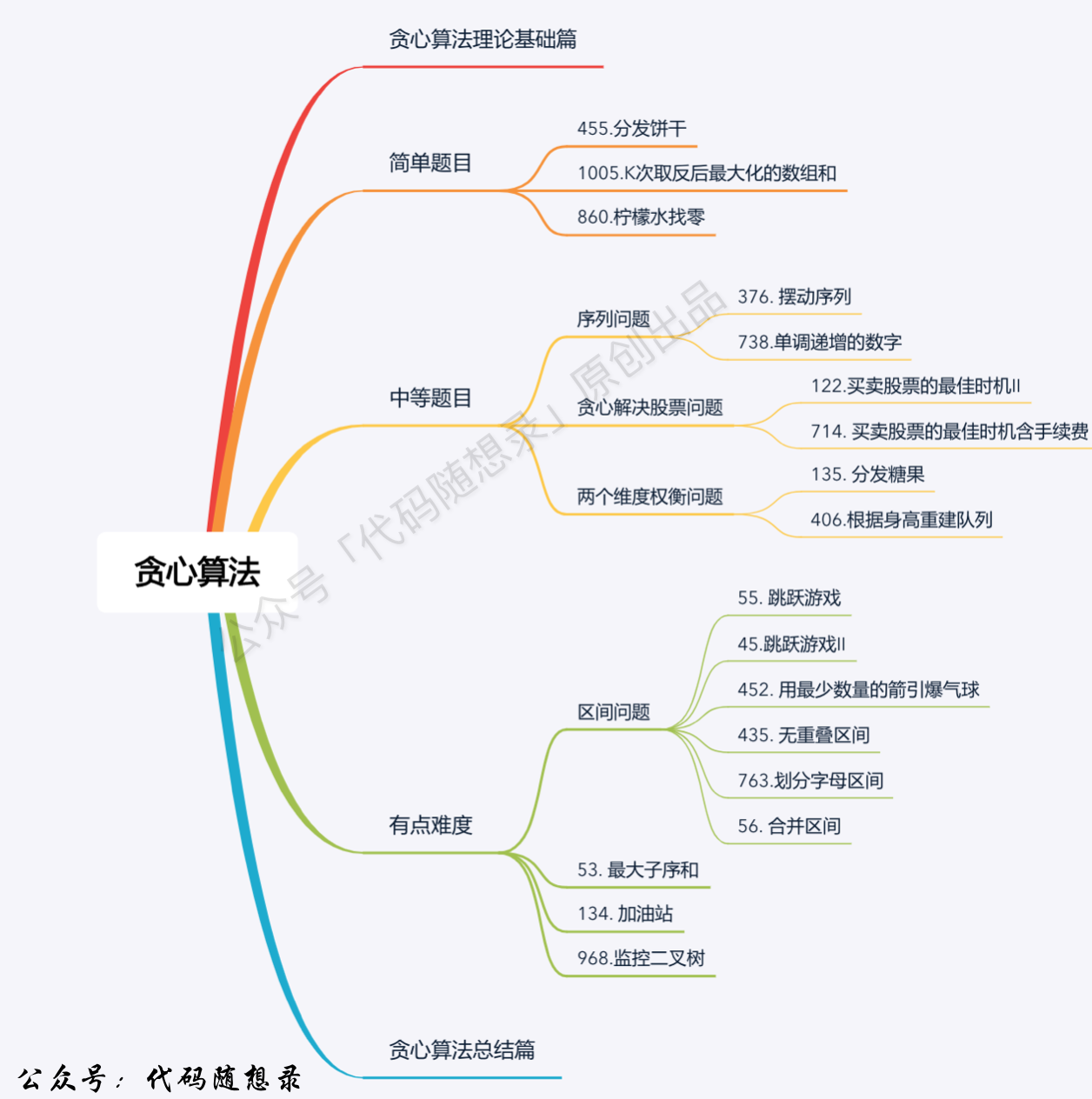-1. [关于贪心算法，你该了解这些！](https://mp.weixin.qq.com/s/O935TaoHE9Eexwe_vSbRAg)
-2. [贪心算法：分发饼干](https://mp.weixin.qq.com/s/YSuLIAYyRGlyxbp9BNC1uw)
-3. [贪心算法：摆动序列](https://mp.weixin.qq.com/s/Xytl05kX8LZZ1iWWqjMoHA)
-4. [贪心算法：最大子序和](https://mp.weixin.qq.com/s/DrjIQy6ouKbpletQr0g1Fg)
-5. [本周小结！（贪心算法系列一）](https://mp.weixin.qq.com/s/KQ2caT9GoVXgB1t2ExPncQ)
-6. [贪心算法：买卖股票的最佳时机II](https://mp.weixin.qq.com/s/VsTFA6U96l18Wntjcg3fcg)
-7. [贪心算法：跳跃游戏](https://mp.weixin.qq.com/s/606_N9j8ACKCODoCbV1lSA)
-8. [贪心算法：跳跃游戏II](https://mp.weixin.qq.com/s/kJBcsJ46DKCSjT19pxrNYg)
-9. [贪心算法：K次取反后最大化的数组和](https://mp.weixin.qq.com/s/dMTzBBVllRm_Z0aaWvYazA)
-10. [本周小结！（贪心算法系列二）](https://mp.weixin.qq.com/s/RiQri-4rP9abFmq_mlXNiQ)
-11. [贪心算法：加油站](https://mp.weixin.qq.com/s/aDbiNuEZIhy6YKgQXvKELw)
-12. [贪心算法：分发糖果](https://mp.weixin.qq.com/s/8MwlgFfvaNYmjGwjuMlETQ)
-13. [贪心算法：柠檬水找零](https://mp.weixin.qq.com/s/0kT4P-hzY7H6Ae0kjQqnZg)
-14. [贪心算法：根据身高重建队列](https://mp.weixin.qq.com/s/-2TgZVdOwS-DvtbjjDEbfw)
-15. [本周小结！（贪心算法系列三）](https://mp.weixin.qq.com/s/JfeuK6KgmifscXdpEyIm-g)
-16. [贪心算法：根据身高重建队列（续集）](https://mp.weixin.qq.com/s/K-pRN0lzR-iZhoi-1FgbSQ)
-17. [贪心算法：用最少数量的箭引爆气球](https://mp.weixin.qq.com/s/HxVAJ6INMfNKiGwI88-RFw)
-18. [贪心算法：无重叠区间](https://mp.weixin.qq.com/s/oFOEoW-13Bm4mik-aqAOmw)
-19. [贪心算法：划分字母区间](https://mp.weixin.qq.com/s/pdX4JwV1AOpc_m90EcO2Hw)
-20. [贪心算法：合并区间](https://mp.weixin.qq.com/s/royhzEM5tOkUFwUGrNStpw)
-21. [本周小结！（贪心算法系列四）](https://mp.weixin.qq.com/s/zAMHT6JfB19ZSJNP713CAQ)
-22. [贪心算法：单调递增的数字](https://mp.weixin.qq.com/s/TAKO9qPYiv6KdMlqNq_ncg)
-23. [贪心算法：买卖股票的最佳时机含手续费](https://mp.weixin.qq.com/s/olWrUuDEYw2Jx5rMeG7XAg)
-24. [贪心算法：我要监控二叉树！](https://mp.weixin.qq.com/s/kCxlLLjWKaE6nifHC3UL2Q)
-25. [贪心算法：总结篇！（每逢总结必经典）](https://mp.weixin.qq.com/s/ItyoYNr0moGEYeRtcjZL3Q)
+1. [关于贪心算法，你该了解这些！](./problems/贪心算法理论基础.md)
+2. [贪心算法：分发饼干](./problems/0455.分发饼干.md)
+3. [贪心算法：摆动序列](./problems/0376.摆动序列.md)
+4. [贪心算法：最大子序和](./problems/0053.最大子序和.md)
+5. [本周小结！（贪心算法系列一）](./problems/周总结/20201126贪心周末总结.md)
+6. [贪心算法：买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II.md)
+7. [贪心算法：跳跃游戏](./problems/0055.跳跃游戏.md)
+8. [贪心算法：跳跃游戏II](./problems/0045.跳跃游戏II.md)
+9. [贪心算法：K次取反后最大化的数组和](./problems/1005.K次取反后最大化的数组和.md)
+10. [本周小结！（贪心算法系列二）](./problems/周总结/20201203贪心周末总结.md)
+11. [贪心算法：加油站](./problems/0134.加油站.md)
+12. [贪心算法：分发糖果](./problems/0135.分发糖果.md)
+13. [贪心算法：柠檬水找零](./problems/0860.柠檬水找零.md)
+14. [贪心算法：根据身高重建队列](./problems/0406.根据身高重建队列.md)
+15. [本周小结！（贪心算法系列三）](./problems/周总结/20201217贪心周末总结.md)
+16. [贪心算法：根据身高重建队列（续集）](./problems/根据身高重建队列（vector原理讲解）.md)
+17. [贪心算法：用最少数量的箭引爆气球](./problems/0452.用最少数量的箭引爆气球.md)
+18. [贪心算法：无重叠区间](./problems/0435.无重叠区间.md)
+19. [贪心算法：划分字母区间](./problems/0763.划分字母区间.md)
+20. [贪心算法：合并区间](./problems/0056.合并区间.md)
+21. [本周小结！（贪心算法系列四）](./problems/周总结/20201224贪心周末总结.md)
+22. [贪心算法：单调递增的数字](./problems/0738.单调递增的数字.md)
+23. [贪心算法：买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费.md)
+24. [贪心算法：我要监控二叉树！](./problems/0968.监控二叉树.md)
+25. [贪心算法：总结篇！（每逢总结必经典）](./problems/贪心算法总结篇.md)
## 动态规划
动态规划专题已经开始啦，来不及解释了，小伙伴们上车别掉队！
-1. [关于动态规划，你该了解这些！](https://mp.weixin.qq.com/s/ocZwfPlCWrJtVGACqFNAag)
-2. [动态规划：斐波那契数](https://mp.weixin.qq.com/s/ko0zLJplF7n_4TysnPOa_w)
-3. [动态规划：爬楼梯](https://mp.weixin.qq.com/s/Ohop0jApSII9xxOMiFhGIw)
-4. [动态规划：使用最小花费爬楼梯](https://mp.weixin.qq.com/s/djZB9gkyLFAKcQcSvKDorA)
-5. [本周小结！（动态规划系列一）](https://mp.weixin.qq.com/s/95VqGEDhtBBBSb-rM4QSMA)
-6. [动态规划：不同路径](https://mp.weixin.qq.com/s/MGgGIt4QCpFMROE9X9he_A)
-7. [动态规划：不同路径还不够，要有障碍！](https://mp.weixin.qq.com/s/lhqF0O4le9-wvalptOVOww)
-8. [动态规划：整数拆分，你要怎么拆？](https://mp.weixin.qq.com/s/cVbyHrsWH_Rfzlj-ESr01A)
-9. [动态规划：不同的二叉搜索树](https://mp.weixin.qq.com/s/8VE8pDrGxTf8NEVYBDwONw)
-10. [本周小结！（动态规划系列二）](https://mp.weixin.qq.com/s/VVsDwTP57g1f9aVsg6wShw)
+
+1. [关于动态规划，你该了解这些！](./problems/动态规划理论基础.md)
+2. [动态规划：斐波那契数](./problems/0509.斐波那契数.md)
+3. [动态规划：爬楼梯](./problems/0070.爬楼梯.md)
+4. [动态规划：使用最小花费爬楼梯](./problems/0746.使用最小花费爬楼梯.md)
+5. [本周小结！（动态规划系列一）](./problems/周总结/20210107动规周末总结.md)
+6. [动态规划：不同路径](./problems/0062.不同路径.md)
+7. [动态规划：不同路径还不够，要有障碍！](./problems/0063.不同路径II.md)
+8. [动态规划：整数拆分，你要怎么拆？](./problems/0343.整数拆分.md)
+9. [动态规划：不同的二叉搜索树](./problems/0096.不同的二叉搜索树.md)
+10. [本周小结！（动态规划系列二）](./problems/周总结/20210114动规周末总结.md)
背包问题系列：
-
+
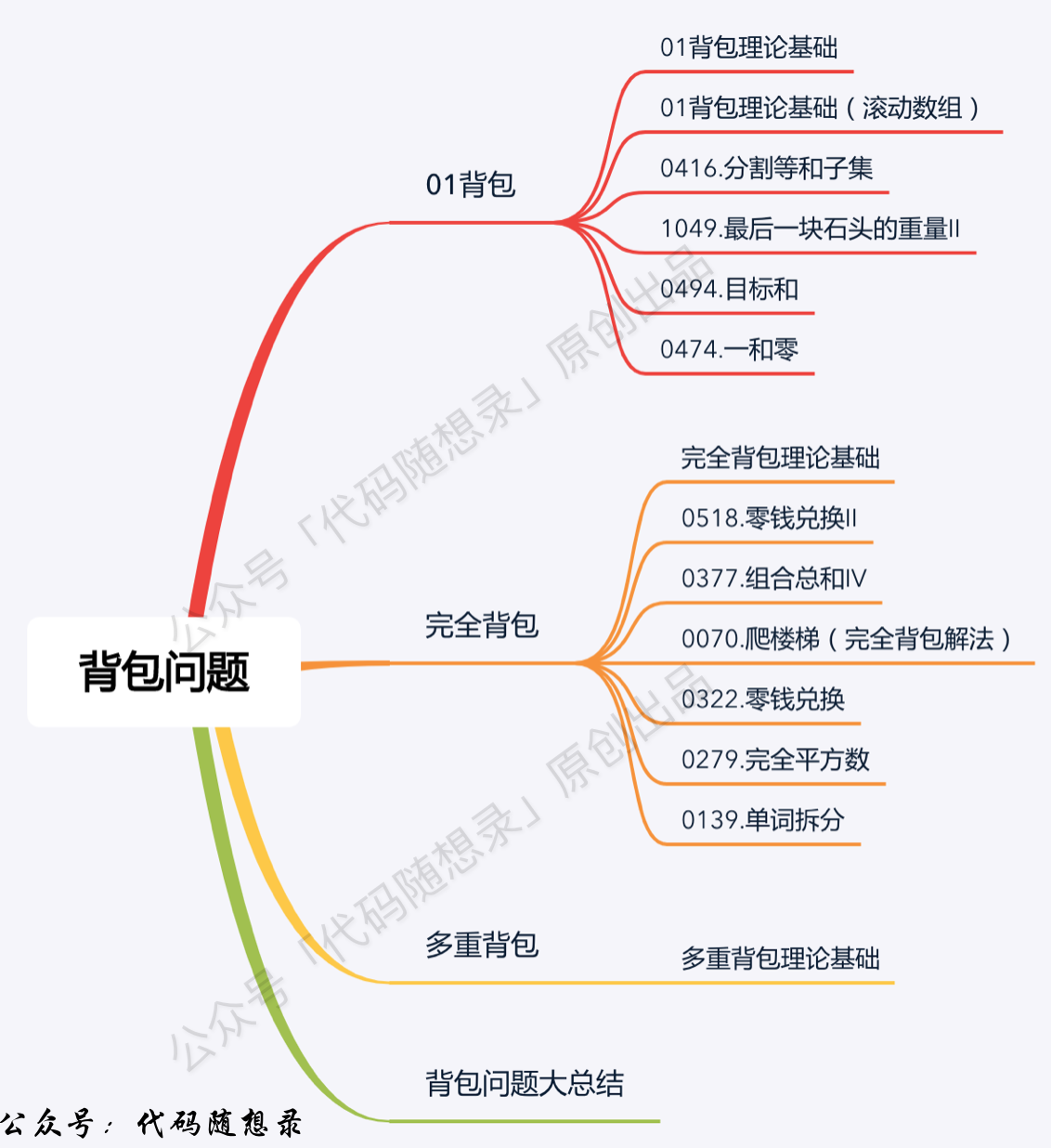-11. [动态规划：关于01背包问题，你该了解这些！](https://mp.weixin.qq.com/s/FwIiPPmR18_AJO5eiidT6w)
-12. [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://mp.weixin.qq.com/s/M4uHxNVKRKm5HPjkNZBnFA)
-13. [动态规划：分割等和子集可以用01背包！](https://mp.weixin.qq.com/s/sYw3QtPPQ5HMZCJcT4EaLQ)
-14. [动态规划：最后一块石头的重量 II](https://mp.weixin.qq.com/s/WbwAo3jaUaNJjvhHgq0BGg)
-15. [本周小结！（动态规划系列三）](https://mp.weixin.qq.com/s/7emRqR1O3scH63jbaE678A)
-16. [动态规划：目标和！](https://mp.weixin.qq.com/s/2pWmaohX75gwxvBENS-NCw)
-17. [动态规划：一和零！](https://mp.weixin.qq.com/s/x-u3Dsp76DlYqtCe0xEKJw)
-18. [动态规划：关于完全背包，你该了解这些！](https://mp.weixin.qq.com/s/akwyxlJ4TLvKcw26KB9uJw)
-19. [动态规划：给你一些零钱，你要怎么凑？](https://mp.weixin.qq.com/s/PlowDsI4WMBOzf3q80AksQ)
-20. [本周小结！（动态规划系列四）](https://mp.weixin.qq.com/s/vfEXwcOlrSBBcv9gg8VDJQ)
-21. [动态规划：Carl称它为排列总和！](https://mp.weixin.qq.com/s/Iixw0nahJWQgbqVNk8k6gA)
-22. [动态规划：以前我没得选，现在我选择再爬一次！](https://mp.weixin.qq.com/s/e_wacnELo-2PG76EjrUakA)
-23. [动态规划： 给我个机会，我再兑换一次零钱](https://mp.weixin.qq.com/s/dyk-xNilHzNtVdPPLObSeQ)
-24. [动态规划：一样的套路，再求一次完全平方数](https://mp.weixin.qq.com/s/VfJT78p7UGpDZsapKF_QJQ)
-25. [本周小结！（动态规划系列五）](https://mp.weixin.qq.com/s/znj-9j8mWymRFaPjJN2Qnw)
-26. [动态规划：单词拆分](https://mp.weixin.qq.com/s/3Spx1B6MbIYjS8YkVbByzA)
-27. [动态规划：关于多重背包，你该了解这些！](https://mp.weixin.qq.com/s/b-UUUmbvG7URWyCjQkiuuQ)
-28. [听说背包问题很难？ 这篇总结篇来拯救你了](https://mp.weixin.qq.com/s/ZOehl3U1mDiyOQjFG1wNJA)
+
+11. [动态规划：关于01背包问题，你该了解这些！](./problems/背包理论基础01背包-1.md)
+12. [动态规划：关于01背包问题，你该了解这些！（滚动数组）](./problems/背包理论基础01背包-2.md)
+13. [动态规划：分割等和子集可以用01背包！](./problems/0416.分割等和子集.md)
+14. [动态规划：最后一块石头的重量 II](./problems/1049.最后一块石头的重量II.md)
+15. [本周小结！（动态规划系列三）](./problems/周总结/20210121动规周末总结.md)
+16. [动态规划：目标和！](./problems/0494.目标和.md)
+17. [动态规划：一和零！](./problems/0474.一和零.md)
+18. [动态规划：关于完全背包，你该了解这些！](./problems/背包问题理论基础完全背包.md)
+19. [动态规划：给你一些零钱，你要怎么凑？](./problems/0518.零钱兑换II.md)
+20. [本周小结！（动态规划系列四）](./problems/周总结/20210128动规周末总结.md)
+21. [动态规划：Carl称它为排列总和！](./problems/0377.组合总和Ⅳ.md)
+22. [动态规划：以前我没得选，现在我选择再爬一次！](./problems/0070.爬楼梯完全背包版本.md)
+23. [动态规划： 给我个机会，我再兑换一次零钱](./problems/0322.零钱兑换.md)
+24. [动态规划：一样的套路，再求一次完全平方数](./problems/0279.完全平方数.md)
+25. [本周小结！（动态规划系列五）](./problems/周总结/20210204动规周末总结.md)
+26. [动态规划：单词拆分](./problems/0139.单词拆分.md)
+27. [动态规划：关于多重背包，你该了解这些！](./problems/背包问题理论基础多重背包.md)
+28. [听说背包问题很难？ 这篇总结篇来拯救你了](./problems/背包总结篇.md)
打家劫舍系列：
-29. [动态规划：开始打家劫舍！](https://mp.weixin.qq.com/s/UZ31WdLEEFmBegdgLkJ8Dw)
-30. [动态规划：继续打家劫舍！](https://mp.weixin.qq.com/s/kKPx4HpH3RArbRcxAVHbeQ)
-31. [动态规划：还要打家劫舍！](https://mp.weixin.qq.com/s/BOJ1lHsxbQxUZffXlgglEQ)
+29. [动态规划：开始打家劫舍！](./problems/0198.打家劫舍.md)
+30. [动态规划：继续打家劫舍！](./problems/0213.打家劫舍II.md)
+31. [动态规划：还要打家劫舍！](./problems/0337.打家劫舍III.md)
股票系列：
-
+
-32. [动态规划：买卖股票的最佳时机](https://mp.weixin.qq.com/s/keWo5qYJY4zmHn3amfXdfQ)
-33. [动态规划：本周我们都讲了这些（系列六）](https://mp.weixin.qq.com/s/GVu-6eF0iNkpVDKRXTPOTA)
-33. [动态规划：买卖股票的最佳时机II](https://mp.weixin.qq.com/s/d4TRWFuhaY83HPa6t5ZL-w)
-34. [动态规划：买卖股票的最佳时机III](https://mp.weixin.qq.com/s/Sbs157mlVDtAR0gbLpdKzg)
-35. [动态规划：买卖股票的最佳时机IV](https://mp.weixin.qq.com/s/jtxZJWAo2y5sUsW647Z5cw)
-36. [动态规划：最佳买卖股票时机含冷冻期](https://mp.weixin.qq.com/s/TczJGFAPnkjH9ET8kwH1OA)
-37. [动态规划：本周我们都讲了这些（系列七）](https://mp.weixin.qq.com/s/vdzDlrEvhXWRzblTnOnzKg)
-38. [动态规划：买卖股票的最佳时机含手续费](https://mp.weixin.qq.com/s/2Cd_uINjerZ25VHH0K2IBQ)
-39. [动态规划：股票系列总结篇](https://mp.weixin.qq.com/s/sC5XyEtDQWkonKnbCvZhDw)
+
+32. [动态规划：买卖股票的最佳时机](./problems/0121.买卖股票的最佳时机.md)
+33. [动态规划：本周我们都讲了这些（系列六）](./problems/周总结/20210225动规周末总结.md)
+33. [动态规划：买卖股票的最佳时机II](./problems/0122.买卖股票的最佳时机II（动态规划）.md)
+34. [动态规划：买卖股票的最佳时机III](./problems/0123.买卖股票的最佳时机III.md)
+35. [动态规划：买卖股票的最佳时机IV](./problems/0188.买卖股票的最佳时机IV.md)
+36. [动态规划：最佳买卖股票时机含冷冻期](./problems/0309.最佳买卖股票时机含冷冻期.md)
+37. [动态规划：本周我们都讲了这些（系列七）](./problems/周总结/20210304动规周末总结.md)
+38. [动态规划：买卖股票的最佳时机含手续费](./problems/0714.买卖股票的最佳时机含手续费（动态规划）.md)
+39. [动态规划：股票系列总结篇](./problems/动态规划-股票问题总结篇.md)
子序列系列：
-40. [动态规划：最长递增子序列](https://mp.weixin.qq.com/s/f8nLO3JGfgriXep_gJQpqQ)
-41. [动态规划：最长连续递增序列](https://mp.weixin.qq.com/s/c0Nn0TtjkTISVdqRsyMmyA)
-42. [动态规划：最长重复子数组](https://mp.weixin.qq.com/s/U5WaWqBwdoxzQDotOdWqZg)
-43. [动态规划：最长公共子序列](https://mp.weixin.qq.com/s/Qq0q4HaE4TyasCTj2WGFOg)
-44. [动态规划：本周我们都讲了这些（系列八）](https://mp.weixin.qq.com/s/KJNNOzGxTYhr1ks7tHvk0g)
-45. [动态规划：不相交的线](https://mp.weixin.qq.com/s/krfYzSYEO8jIoVfyHzR0rw)
-46. [动态规划：最大子序和](https://mp.weixin.qq.com/s/2Xtyi2L4r8sM-BcxgUKmcA)
-47. [动态规划：判断子序列](https://mp.weixin.qq.com/s/2pjT4B4fjfOx5iB6N6xyng)
-48. [动态规划：不同的子序列](https://mp.weixin.qq.com/s/1SULY2XVSROtk_hsoVLu8A)
-49. [动态规划：两个字符串的删除操作](https://mp.weixin.qq.com/s/a8BerpqSf76DCqkPDJrpYg)
-
+
+40. [动态规划：最长递增子序列](./problems/0300.最长上升子序列.md)
+41. [动态规划：最长连续递增序列](./problems/0674.最长连续递增序列.md)
+42. [动态规划：最长重复子数组](./problems/0718.最长重复子数组.md)
+43. [动态规划：最长公共子序列](./problems/1143.最长公共子序列.md)
+45. [动态规划：不相交的线](./problems/1035.不相交的线.md)
+46. [动态规划：最大子序和](./problems/0053.最大子序和（动态规划）.md)
+47. [动态规划：判断子序列](./problems/0392.判断子序列.md)
+48. [动态规划：不同的子序列](./problems/0115.不同的子序列.md)
+49. [动态规划：两个字符串的删除操作](./problems/0583.两个字符串的删除操作.md)
+51. [动态规划：编辑距离](./problems/0072.编辑距离.md)
+52. [为了绝杀编辑距离，Carl做了三步铺垫，你都知道么？](./problems/为了绝杀编辑距离，卡尔做了三步铺垫.md)
+53. [动态规划：回文子串](./problems/0647.回文子串.md)
+54. [动态规划：最长回文子序列](./problems/0516.最长回文子序列.md)
+55. [动态规划总结篇](./problems/动态规划总结篇.md)
（持续更新中....）
+## 单调栈
+
+1. [每日温度](./problems/0739.每日温度.md)
+
## 图论
## 十大排序
@@ -391,22 +418,46 @@
[各类基础算法模板](https://github.com/youngyangyang04/leetcode/blob/master/problems/算法模板.md)
+
+# B站算法视频讲解
+
+以下为[B站「代码随想录」](https://space.bilibili.com/525438321)算法讲解视频：
+
+* [KMP算法（理论篇）](https://www.bilibili.com/video/BV1PD4y1o7nd)
+* [KMP算法（代码篇）](https://www.bilibili.com/video/BV1M5411j7Xx)
+* [回溯算法理论基础](https://www.bilibili.com/video/BV1cy4y167mM)
+* [回溯算法之组合问题（力扣题目：77.组合）](https://www.bilibili.com/video/BV1ti4y1L7cv)
+* [组合问题的剪枝操作（对应力扣题目：77.组合）](https://www.bilibili.com/video/BV1wi4y157er)
+* [组合总和（对应力扣题目：39.组合总和）](https://www.bilibili.com/video/BV1KT4y1M7HJ/)
+* [分割回文串（对应力扣题目：131.分割回文串)](https://www.bilibili.com/video/BV1c54y1e7k6)
+* [二叉树理论基础](https://www.bilibili.com/video/BV1Hy4y1t7ij)
+* [二叉树的递归遍历](https://www.bilibili.com/video/BV1Wh411S7xt)
+* [二叉树的非递归遍历（一）](https://www.bilibili.com/video/BV15f4y1W7i2)
+
+（持续更新中....）
+
+# 贡献者
+
+你可以[点此链接](https://github.com/youngyangyang04/leetcode-master/graphs/contributors)查看LeetCode-Master的所有贡献者。感谢你们补充了LeetCode-Master的其他语言版本，让更多的读者收益于此项目。
+
# 关于作者
大家好，我是程序员Carl，哈工大师兄，ACM 校赛、黑龙江省赛、东北四省赛金牌、亚洲区域赛铜牌获得者，先后在腾讯和百度从事后端技术研发，CSDN博客专家。对算法和C++后端技术有一定的见解，利用工作之余重新刷leetcode。
-**加我的微信，备注：「个人简单介绍」+「组队刷题」**， 拉你进刷题群，每天一道经典题目分析，而且题目不是孤立的，每一道题目之间都是有关系的，都是由浅入深一脉相承的，所以学习效果最好是每篇连续着看，也许之前你会某些知识点，但是一直没有把知识点串起来，这里每天一篇文章就会帮你把知识点串起来。
+加入刷题微信群，备注：「个人简单介绍」 + 组队刷题
-也欢迎找我交流，加微信备注：「个人简单介绍」 + 交流
+也欢迎与我交流，备注：「个人简单介绍」 + 交流，围观朋友圈，做点赞之交（备注没有自我介绍不通过哦）
-# 我的公众号
+# 公众号
更多精彩文章持续更新，微信搜索：「代码随想录」第一时间围观，关注后回复：「666」可以获得所有算法专题原创PDF。
-**每天8：35准时为你推送一篇经典面试题目，帮你梳理算法知识体系，轻松学习算法！**，并且公众号里有大量学习资源，也有我自己的学习心得和方法总结，更有上万录友们在这里打卡学习，**来看看就你知道了，一定会发现相见恨晚！**
+**「代码随想录」每天准时为你推送一篇经典面试题目，帮你梳理算法知识体系，轻松学习算法！**，并且公众号里有大量学习资源，也有我自己的学习心得和方法总结，更有上万录友们在这里打卡学习。
+
+**来看看就知道了，你会发现相见恨晚！**
diff --git a/pics/公众号.png b/pics/公众号.png
index 9873ef42..eeec00ad 100644
Binary files a/pics/公众号.png and b/pics/公众号.png differ
diff --git a/pics/公众号二维码.jpg b/pics/公众号二维码.jpg
new file mode 100644
index 00000000..a91b2494
Binary files /dev/null and b/pics/公众号二维码.jpg differ
diff --git a/pics/知识星球.png b/pics/知识星球.png
new file mode 100644
index 00000000..43a5c6b3
Binary files /dev/null and b/pics/知识星球.png differ
diff --git a/problems/0001.两数之和.md b/problems/0001.两数之和.md
new file mode 100644
index 00000000..5be94996
--- /dev/null
+++ b/problems/0001.两数之和.md
@@ -0,0 +1,213 @@
+
+
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ + +## 1. 两数之和 + +https://leetcode-cn.com/problems/two-sum/ + +给定一个整数数组 nums 和一个目标值 target，请你在该数组中找出和为目标值的那 两个 整数，并返回他们的数组下标。 + +你可以假设每种输入只会对应一个答案。但是，数组中同一个元素不能使用两遍。 + +**示例:** + +给定 nums = [2, 7, 11, 15], target = 9 + +因为 nums[0] + nums[1] = 2 + 7 = 9 + +所以返回 [0, 1] + + +## 思路 + +很明显暴力的解法是两层for循环查找，时间复杂度是O(n^2)。 + +建议大家做这道题目之前，先做一下这两道 +* [242. 有效的字母异位词](https://mp.weixin.qq.com/s/ffS8jaVFNUWyfn_8T31IdA) +* [349. 两个数组的交集](https://mp.weixin.qq.com/s/aMSA5zrp3jJcLjuSB0Es2Q) + +[242. 有效的字母异位词](https://mp.weixin.qq.com/s/ffS8jaVFNUWyfn_8T31IdA) 这道题目是用数组作为哈希表来解决哈希问题，[349. 两个数组的交集](https://mp.weixin.qq.com/s/aMSA5zrp3jJcLjuSB0Es2Q)这道题目是通过set作为哈希表来解决哈希问题。 + +本题呢，则要使用map，那么来看一下使用数组和set来做哈希法的局限。 + +* 数组的大小是受限制的，而且如果元素很少，而哈希值太大会造成内存空间的浪费。 +* set是一个集合，里面放的元素只能是一个key，而两数之和这道题目，不仅要判断y是否存在而且还要记录y的下表位置，因为要返回x 和 y的下表。所以set 也不能用。 + +此时就要选择另一种数据结构：map ，map是一种key value的存储结构，可以用key保存数值，用value在保存数值所在的下表。 + +C++中map，有三种类型： + +|映射 |底层实现 | 是否有序 |数值是否可以重复 | 能否更改数值|查询效率 |增删效率| +|---|---| --- |---| --- | --- | ---| +|std::map |红黑树 |key有序 |key不可重复 |key不可修改 | O(logn)|O(logn) | +|std::multimap | 红黑树|key有序 | key可重复 | key不可修改|O(logn) |O(logn) | +|std::unordered_map |哈希表 | key无序 |key不可重复 |key不可修改 |O(1) | O(1)| + +std::unordered_map 底层实现为哈希表，std::map 和std::multimap 的底层实现是红黑树。 + +同理，std::map 和std::multimap 的key也是有序的（这个问题也经常作为面试题，考察对语言容器底层的理解）。 更多哈希表的理论知识请看[关于哈希表，你该了解这些！](https://mp.weixin.qq.com/s/RSUANESA_tkhKhYe3ZR8Jg)。 + +**这道题目中并不需要key有序，选择std::unordered_map 效率更高！** + +解题思路动画如下： + + + + +C++代码： + +```C++ +class Solution { +public: + vector
+
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ + + +> 用哈希表解决了[两数之和](https://mp.weixin.qq.com/s/uVAtjOHSeqymV8FeQbliJQ)，那么三数之和呢？ + +# 第15题. 三数之和 + +https://leetcode-cn.com/problems/3sum/ + +给你一个包含 n 个整数的数组 nums，判断 nums 中是否存在三个元素 a，b，c ，使得 a + b + c = 0 ？请你找出所有满足条件且不重复的三元组。 + +**注意：** 答案中不可以包含重复的三元组。 + +示例： + +给定数组 nums = [-1, 0, 1, 2, -1, -4]， + +满足要求的三元组集合为： +[ + [-1, 0, 1], + [-1, -1, 2] +] + + +# 思路 + +**注意[0， 0， 0， 0] 这组数据** + +## 哈希解法 + +两层for循环就可以确定 a 和b 的数值了，可以使用哈希法来确定 0-(a+b) 是否在 数组里出现过，其实这个思路是正确的，但是我们有一个非常棘手的问题，就是题目中说的不可以包含重复的三元组。 + +把符合条件的三元组放进vector中，然后在去去重，这样是非常费时的，很容易超时，也是这道题目通过率如此之低的根源所在。 + +去重的过程不好处理，有很多小细节，如果在面试中很难想到位。 + +时间复杂度可以做到O(n^2)，但还是比较费时的，因为不好做剪枝操作。 + +大家可以尝试使用哈希法写一写，就知道其困难的程度了。 + +哈希法C++代码: +```C++ +class Solution { +public: + vector
+
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ + +# 17.电话号码的字母组合 + +题目链接：https://leetcode-cn.com/problems/letter-combinations-of-a-phone-number/ + +给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。 + +给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。 + +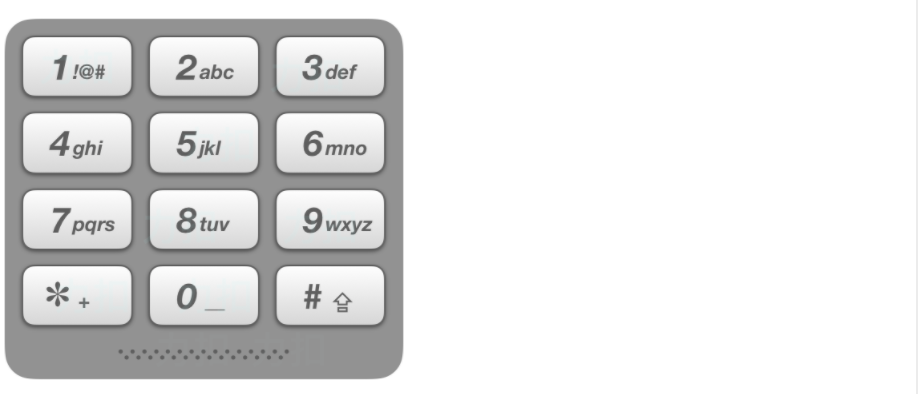 + +示例: +输入："23" +输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]. + +说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。 + +# 思路 + +从示例上来说，输入"23"，最直接的想法就是两层for循环遍历了吧，正好把组合的情况都输出了。 + +如果输入"233"呢，那么就三层for循环，如果"2333"呢，就四层for循环....... + +大家应该感觉出和[回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)遇到的一样的问题，就是这for循环的层数如何写出来，此时又是回溯法登场的时候了。 + +理解本题后，要解决如下三个问题： + +1. 数字和字母如何映射 +2. 两个字母就两个for循环，三个字符我就三个for循环，以此类推，然后发现代码根本写不出来 +3. 输入1 * #按键等等异常情况 + +## 数字和字母如何映射 + +可以使用map或者定义一个二位数组，例如：string letterMap[10]，来做映射，我这里定义一个二维数组，代码如下： + +``` +const string letterMap[10] = { + "", // 0 + "", // 1 + "abc", // 2 + "def", // 3 + "ghi", // 4 + "jkl", // 5 + "mno", // 6 + "pqrs", // 7 + "tuv", // 8 + "wxyz", // 9 +}; +``` + +## 回溯法来解决n个for循环的问题 + +对于回溯法还不了解的同学看这篇：[关于回溯算法，你该了解这些！](https://mp.weixin.qq.com/s/gjSgJbNbd1eAA5WkA-HeWw) + + +例如：输入："23"，抽象为树形结构，如图所示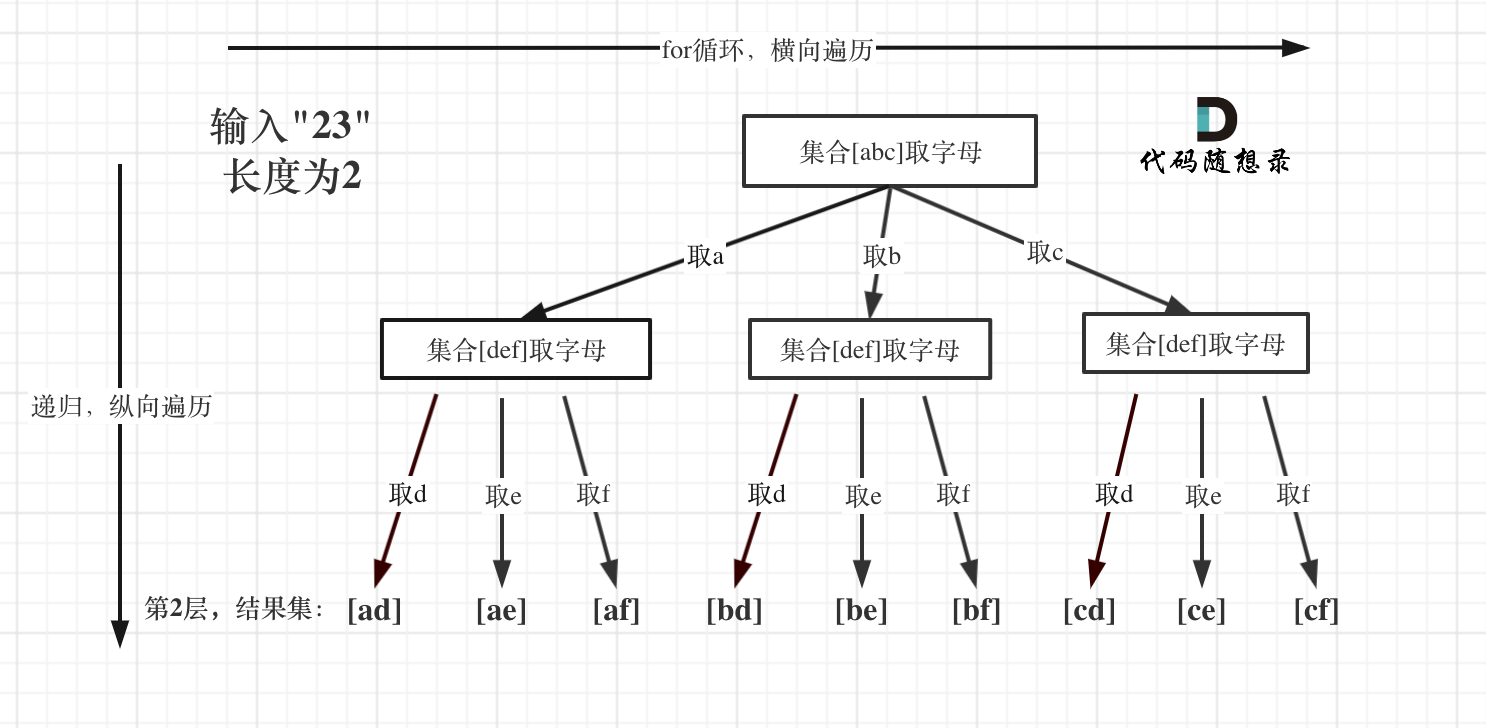： + + + +图中可以看出遍历的深度，就是输入"23"的长度，而叶子节点就是我们要收集的结果，输出["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"]。 + +回溯三部曲： + +* 确定回溯函数参数 + +首先需要一个字符串s来收集叶子节点的结果，然后用一个字符串数组result保存起来，这两个变量我依然定义为全局。 + +再来看参数，参数指定是有题目中给的string digits，然后还要有一个参数就是int型的index。 + +注意这个index可不是 [回溯算法：求组合问题！](https://mp.weixin.qq.com/s/OnBjbLzuipWz_u4QfmgcqQ)和[回溯算法：求组合总和！](https://mp.weixin.qq.com/s/HX7WW6ixbFZJASkRnCTC3w)中的startIndex了。 + +这个index是记录遍历第几个数字了，就是用来遍历digits的（题目中给出数字字符串），同时index也表示树的深度。 + +代码如下： + +``` +vector
diff --git a/problems/0018.四数之和.md b/problems/0018.四数之和.md
new file mode 100644
index 00000000..0caf12be
--- /dev/null
+++ b/problems/0018.四数之和.md
@@ -0,0 +1,244 @@
+
+
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ + +> 一样的道理，能解决四数之和 +> 那么五数之和、六数之和、N数之和呢？ + +# 第18题. 四数之和 + +https://leetcode-cn.com/problems/4sum/ + +题意：给定一个包含 n 个整数的数组 nums 和一个目标值 target，判断 nums 中是否存在四个元素 a，b，c 和 d ，使得 a + b + c + d 的值与 target 相等？找出所有满足条件且不重复的四元组。 + +**注意：** + +答案中不可以包含重复的四元组。 + +示例： +给定数组 nums = [1, 0, -1, 0, -2, 2]，和 target = 0。 +满足要求的四元组集合为： +[ + [-1, 0, 0, 1], + [-2, -1, 1, 2], + [-2, 0, 0, 2] +] + +# 思路 + +四数之和，和[15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg)是一个思路，都是使用双指针法, 基本解法就是在[15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg) 的基础上再套一层for循环。 + +但是有一些细节需要注意，例如： 不要判断`nums[k] > target` 就返回了，三数之和 可以通过 `nums[i] > 0` 就返回了，因为 0 已经是确定的数了，四数之和这道题目 target是任意值。（大家亲自写代码就能感受出来） + +[15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg)的双指针解法是一层for循环num[i]为确定值，然后循环内有left和right下表作为双指针，找到nums[i] + nums[left] + nums[right] == 0。 + +四数之和的双指针解法是两层for循环nums[k] + nums[i]为确定值，依然是循环内有left和right下表作为双指针，找出nums[k] + nums[i] + nums[left] + nums[right] == target的情况，三数之和的时间复杂度是O(n^2)，四数之和的时间复杂度是O(n^3) 。 + +那么一样的道理，五数之和、六数之和等等都采用这种解法。 + +对于[15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg)双指针法就是将原本暴力O(n^3)的解法，降为O(n^2)的解法，四数之和的双指针解法就是将原本暴力O(n^4)的解法，降为O(n^3)的解法。 + +之前我们讲过哈希表的经典题目：[454.四数相加II](https://mp.weixin.qq.com/s/12g_w6RzHuEpFts1pT6BWw)，相对于本题简单很多，因为本题是要求在一个集合中找出四个数相加等于target，同时四元组不能重复。 + +而[454.四数相加II](https://mp.weixin.qq.com/s/12g_w6RzHuEpFts1pT6BWw)是四个独立的数组，只要找到A[i] + B[j] + C[k] + D[l] = 0就可以，不用考虑有重复的四个元素相加等于0的情况，所以相对于本题还是简单了不少！ + +我们来回顾一下，几道题目使用了双指针法。 + +双指针法将时间复杂度O(n^2)的解法优化为 O(n)的解法。也就是降一个数量级，题目如下： + +* [27.移除元素](https://mp.weixin.qq.com/s/RMkulE4NIb6XsSX83ra-Ww) +* [15.三数之和](https://mp.weixin.qq.com/s/QfTNEByq1YlNSXRKEumwHg) +* [18.四数之和](https://mp.weixin.qq.com/s/nQrcco8AZJV1pAOVjeIU_g) + + +操作链表： + +* [206.反转链表](https://mp.weixin.qq.com/s/ckEvIVGcNLfrz6OLOMoT0A) +* [19.删除链表的倒数第N个节点](https://mp.weixin.qq.com/s/gxu65X1343xW_sBrkTz0Eg) +* [面试题 02.07. 链表相交](https://mp.weixin.qq.com/s/BhfFfaGvt9Zs7UmH4YehZw) +* [142题.环形链表II](https://mp.weixin.qq.com/s/gt_VH3hQTqNxyWcl1ECSbQ) + +双指针法在字符串题目中还有很多应用，后面还会介绍到。 + +C++代码 + +```C++ +class Solution { +public: + vector
+
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ + + + +## 19.删除链表的倒数第N个节点 + +题目链接：https://leetcode-cn.com/problems/remove-nth-node-from-end-of-list/ + +给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。 + +进阶：你能尝试使用一趟扫描实现吗？ + +示例 1： + + + +输入：head = [1,2,3,4,5], n = 2 +输出：[1,2,3,5] +示例 2： + +输入：head = [1], n = 1 +输出：[] +示例 3： + +输入：head = [1,2], n = 1 +输出：[1] + + +## 思路 + +双指针的经典应用，如果要删除倒数第n个节点，让fast移动n步，然后让fast和slow同时移动，直到fast指向链表末尾。删掉slow所指向的节点就可以了。 + +思路是这样的，但要注意一些细节。 + +分为如下几步： + +* 首先这里我推荐大家使用虚拟头结点，这样方面处理删除实际头结点的逻辑，如果虚拟头结点不清楚，可以看这篇： [链表：听说用虚拟头节点会方便很多？](https://mp.weixin.qq.com/s/L5aanfALdLEwVWGvyXPDqA) + +* 定义fast指针和slow指针，初始值为虚拟头结点，如图： + +
+
+* fast首先走n + 1步 ，为什么是n+1呢，因为只有这样同时移动的时候slow才能指向删除节点的上一个节点（方便做删除操作），如图：
+
+
+* fast和slow同时移动，之道fast指向末尾，如题：
+
+
+* 删除slow指向的下一个节点，如图：
+
+
+此时不难写出如下C++代码：
+
+```C++
+class Solution {
+public:
+ ListNode* removeNthFromEnd(ListNode* head, int n) {
+ ListNode* dummyHead = new ListNode(0);
+ dummyHead->next = head;
+ ListNode* slow = dummyHead;
+ ListNode* fast = dummyHead;
+ while(n-- && fast != NULL) {
+ fast = fast->next;
+ }
+ fast = fast->next; // fast再提前走一步，因为需要让slow指向删除节点的上一个节点
+ while (fast != NULL) {
+ fast = fast->next;
+ slow = slow->next;
+ }
+ slow->next = slow->next->next;
+ return dummyHead->next;
+ }
+};
+```
+
+
+## 其他语言版本
+
+java:
+
+```java
+class Solution {
+ public ListNode removeNthFromEnd(ListNode head, int n) {
+ ListNode dummy = new ListNode(-1);
+ dummy.next = head;
+
+ ListNode slow = dummy;
+ ListNode fast = dummy;
+ while (n-- > 0) {
+ fast = fast.next;
+ }
+ // 记住 待删除节点slow 的上一节点
+ ListNode prev = null;
+ while (fast != null) {
+ prev = slow;
+ slow = slow.next;
+ fast = fast.next;
+ }
+ // 上一节点的next指针绕过 待删除节点slow 直接指向slow的下一节点
+ prev.next = slow.next;
+ // 释放 待删除节点slow 的next指针, 这句删掉也能AC
+ slow.next = null;
+
+ return dummy.next;
+ }
+}
+```
+
+Python:
+```python
+# Definition for singly-linked list.
+# class ListNode:
+# def __init__(self, val=0, next=None):
+# self.val = val
+# self.next = next
+class Solution:
+ def removeNthFromEnd(self, head: ListNode, n: int) -> ListNode:
+ head_dummy = ListNode()
+ head_dummy.next = head
+
+ slow, fast = head_dummy, head_dummy
+ while(n!=0): #fast先往前走n步
+ fast = fast.next
+ n -= 1
+ while(fast.next!=None):
+ slow = slow.next
+ fast = fast.next
+ #fast 走到结尾后，slow的下一个节点为倒数第N个节点
+ slow.next = slow.next.next #删除
+ return head_dummy.next
+```
+Go:
+```Go
+/**
+ * Definition for singly-linked list.
+ * type ListNode struct {
+ * Val int
+ * Next *ListNode
+ * }
+ */
+func removeNthFromEnd(head *ListNode, n int) *ListNode {
+ dummyHead := &ListNode{}
+ dummyHead.Next = head
+ cur := head
+ prev := dummyHead
+ i := 1
+ for cur != nil {
+ cur = cur.Next
+ if i > n {
+ prev = prev.Next
+ }
+ i++
+ }
+ prev.Next = prev.Next.Next
+ return dummyHead.Next
+}
+```
+
+JavaScript:
+
+```js
+/**
+ * @param {ListNode} head
+ * @param {number} n
+ * @return {ListNode}
+ */
+var removeNthFromEnd = function(head, n) {
+ let ret = new ListNode(0, head),
+ slow = fast = ret;
+ while(n--) fast = fast.next;
+ if(!fast) return ret.next;
+ while (fast.next) {
+ fast = fast.next;
+ slow = slow.next
+ };
+ slow.next = slow.next.next;
+ return ret.next;
+};
+```
+
+-----------------------
+* 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站视频：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
+
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ + + +> 数据结构与算法应用往往隐藏在我们看不到的地方 + +# 20. 有效的括号 + +https://leetcode-cn.com/problems/valid-parentheses/ + +给定一个只包括 '('，')'，'{'，'}'，'['，']' 的字符串，判断字符串是否有效。 + +有效字符串需满足： +* 左括号必须用相同类型的右括号闭合。 +* 左括号必须以正确的顺序闭合。 +* 注意空字符串可被认为是有效字符串。 + +示例 1: +* 输入: "()" +* 输出: true + +示例 2: +* 输入: "()[]{}" +* 输出: true + +示例 3: +* 输入: "(]" +* 输出: false + +示例 4: +* 输入: "([)]" +* 输出: false + +示例 5: +* 输入: "{[]}" +* 输出: true + +# 思路 + +## 题外话 + +**括号匹配是使用栈解决的经典问题。** + +题意其实就像我们在写代码的过程中，要求括号的顺序是一样的，有左括号，相应的位置必须要有右括号。 + +如果还记得编译原理的话，编译器在 词法分析的过程中处理括号、花括号等这个符号的逻辑，也是使用了栈这种数据结构。 + +再举个例子，linux系统中，cd这个进入目录的命令我们应该再熟悉不过了。 + +``` +cd a/b/c/../../ +``` + +这个命令最后进入a目录，系统是如何知道进入了a目录呢 ，这就是栈的应用（其实可以出一道相应的面试题了） + +所以栈在计算机领域中应用是非常广泛的。 + +有的同学经常会想学的这些数据结构有什么用，也开发不了什么软件，大多数同学说的软件应该都是可视化的软件例如APP、网站之类的，那都是非常上层的应用了，底层很多功能的实现都是基础的数据结构和算法。 + +**所以数据结构与算法的应用往往隐藏在我们看不到的地方！** + +这里我就不过多展开了，先来看题。 + +## 进入正题 + +由于栈结构的特殊性，非常适合做对称匹配类的题目。 + +首先要弄清楚，字符串里的括号不匹配有几种情况。 + +**一些同学，在面试中看到这种题目上来就开始写代码，然后就越写越乱。** + +建议要写代码之前要分析好有哪几种不匹配的情况，如果不动手之前分析好，写出的代码也会有很多问题。 + +先来分析一下 这里有三种不匹配的情况， + +1. 第一种情况，字符串里左方向的括号多余了 ，所以不匹配。 +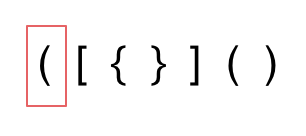 +2. 第二种情况，括号没有多余，但是 括号的类型没有匹配上。 +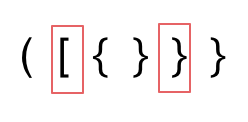 +3. 第三种情况，字符串里右方向的括号多余了，所以不匹配。 +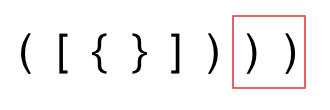 + +我们的代码只要覆盖了这三种不匹配的情况，就不会出问题，可以看出 动手之前分析好题目的重要性。 + +动画如下： + + + + +第一种情况：已经遍历完了字符串，但是栈不为空，说明有相应的左括号没有右括号来匹配，所以return false + +第二种情况：遍历字符串匹配的过程中，发现栈里没有要匹配的字符。所以return false + +第三种情况：遍历字符串匹配的过程中，栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号return false + +那么什么时候说明左括号和右括号全都匹配了呢，就是字符串遍历完之后，栈是空的，就说明全都匹配了。 + +分析完之后，代码其实就比较好写了， + +但还有一些技巧，在匹配左括号的时候，右括号先入栈，就只需要比较当前元素和栈顶相不相等就可以了，比左括号先入栈代码实现要简单的多了！ + +实现C++代码如下： + + +```C++ +class Solution { +public: + bool isValid(string s) { + stack
+
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ + +## 24. 两两交换链表中的节点 + +给定一个链表，两两交换其中相邻的节点，并返回交换后的链表。 + +你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。 + + +
+
+## 思路
+
+这道题目正常模拟就可以了。
+
+建议使用虚拟头结点，这样会方便很多，要不然每次针对头结点（没有前一个指针指向头结点），还要单独处理。
+
+对虚拟头结点的操作，还不熟悉的话，可以看这篇[链表：听说用虚拟头节点会方便很多？](https://mp.weixin.qq.com/s/L5aanfALdLEwVWGvyXPDqA)。
+
+接下来就是交换相邻两个元素了，**此时一定要画图，不画图，操作多个指针很容易乱，而且要操作的先后顺序**
+
+初始时，cur指向虚拟头结点，然后进行如下三步：
+
+
+
+操作之后，链表如下：
+
+
+
+看这个可能就更直观一些了：
+
+
+
+
+对应的C++代码实现如下： （注释中详细和如上图中的三步做对应）
+
+```C++
+class Solution {
+public:
+ ListNode* swapPairs(ListNode* head) {
+ ListNode* dummyHead = new ListNode(0); // 设置一个虚拟头结点
+ dummyHead->next = head; // 将虚拟头结点指向head，这样方面后面做删除操作
+ ListNode* cur = dummyHead;
+ while(cur->next != nullptr && cur->next->next != nullptr) {
+ ListNode* tmp = cur->next; // 记录临时节点
+ ListNode* tmp1 = cur->next->next->next; // 记录临时节点
+
+ cur->next = cur->next->next; // 步骤一
+ cur->next->next = tmp; // 步骤二
+ cur->next->next->next = tmp1; // 步骤三
+
+ cur = cur->next->next; // cur移动两位，准备下一轮交换
+ }
+ return dummyHead->next;
+ }
+};
+```
+* 时间复杂度：$O(n)$
+* 空间复杂度：$O(1)$
+
+## 拓展
+
+**这里还是说一下，大家不必太在意力扣上执行用时，打败多少多少用户，这个统计不准确的。**
+
+做题的时候自己能分析出来时间复杂度就可以了，至于力扣上执行用时，大概看一下就行。
+
+上面的代码我第一次提交执行用时8ms，打败6.5%的用户，差点吓到我了。
+
+心想应该没有更好的方法了吧，也就O(n)的时间复杂度，重复提交几次，这样了：
+
+
+
+力扣上的统计如果两份代码是 100ms 和 300ms的耗时，其实是需要注意的。
+
+如果一个是 4ms 一个是 12ms，看上去好像是一个打败了80%，一个打败了20%，其实是没有差别的。 只不过是力扣上统计的误差而已。
+
+
+## 其他语言版本
+
+
+Java：
+
+```Java
+// 递归版本
+class Solution {
+ public ListNode swapPairs(ListNode head) {
+ // base case 退出提交
+ if(head == null || head.next == null) return head;
+ // 获取当前节点的下一个节点
+ ListNode next = head.next;
+ // 进行递归
+ ListNode newNode = swapPairs(next.next);
+ // 这里进行交换
+ next.next = head;
+ head.next = newNode;
+
+ return next;
+ }
+}
+```
+
+```java
+// 虚拟头结点
+class Solution {
+ public ListNode swapPairs(ListNode head) {
+
+ ListNode dummyNode = new ListNode(0);
+ dummyNode.next = head;
+ ListNode prev = dummyNode;
+
+ while (prev.next != null && prev.next.next != null) {
+ ListNode temp = head.next.next; // 缓存 next
+ prev.next = head.next; // 将 prev 的 next 改为 head 的 next
+ head.next.next = head; // 将 head.next(prev.next) 的next，指向 head
+ head.next = temp; // 将head 的 next 接上缓存的temp
+ prev = head; // 步进1位
+ head = head.next; // 步进1位
+ }
+ return dummyNode.next;
+ }
+}
+```
+
+Python：
+```python
+class Solution:
+ def swapPairs(self, head: ListNode) -> ListNode:
+ dummy = ListNode(0) #设置一个虚拟头结点
+ dummy.next = head
+ cur = dummy
+ while cur.next and cur.next.next:
+ tmp = cur.next #记录临时节点
+ tmp1 = cur.next.next.next #记录临时节点
+
+ cur.next = cur.next.next #步骤一
+ cur.next.next = tmp #步骤二
+ cur.next.next.next = tmp1 #步骤三
+
+ cur = cur.next.next #cur移动两位，准备下一轮交换
+ return dummy.next
+```
+
+Go：
+```go
+func swapPairs(head *ListNode) *ListNode {
+ dummy := &ListNode{
+ Next: head,
+ }
+ //head=list[i]
+ //pre=list[i-1]
+ pre := dummy
+ for head != nil && head.Next != nil {
+ pre.Next = head.Next
+ next := head.Next.Next
+ head.Next.Next = head
+ head.Next = next
+ //pre=list[(i+2)-1]
+ pre = head
+ //head=list[(i+2)]
+ head = next
+ }
+ return dummy.Next
+}
+```
+
+```go
+// 递归版本
+func swapPairs(head *ListNode) *ListNode {
+ if head == nil || head.Next == nil {
+ return head
+ }
+ next := head.Next
+ head.Next = swapPairs(next.Next)
+ next.Next = head
+ return next
+}
+```
+
+Javascript:
+```javascript
+var swapPairs = function (head) {
+ let ret = new ListNode(0, head), temp = ret;
+ while (temp.next && temp.next.next) {
+ let cur = temp.next.next, pre = temp.next;
+ pre.next = cur.next;
+ cur.next = pre;
+ temp.next = cur;
+ temp = pre;
+ }
+ return ret.next;
+};
+```
+
+
+-----------------------
+* 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
+* B站视频：[代码随想录](https://space.bilibili.com/525438321)
+* 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
+
+
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ + +## 27. 移除元素 + +题目地址：https://leetcode-cn.com/problems/remove-element/ + +给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。 + +不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并**原地**修改输入数组。 + +元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。 + +示例 1: +给定 nums = [3,2,2,3], val = 3, +函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。 +你不需要考虑数组中超出新长度后面的元素。 + +示例 2: +给定 nums = [0,1,2,2,3,0,4,2], val = 2, +函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。 + +**你不需要考虑数组中超出新长度后面的元素。** + +## 思路 + +有的同学可能说了，多余的元素，删掉不就得了。 + +**要知道数组的元素在内存地址中是连续的，不能单独删除数组中的某个元素，只能覆盖。** + +数组的基础知识可以看这里[程序员算法面试中，必须掌握的数组理论知识](https://mp.weixin.qq.com/s/c2KABb-Qgg66HrGf8z-8Og)。 + +### 暴力解法 + +这个题目暴力的解法就是两层for循环，一个for循环遍历数组元素 ，第二个for循环更新数组。 + +删除过程如下： + + + +很明显暴力解法的时间复杂度是O(n^2)，这道题目暴力解法在leetcode上是可以过的。 + +代码如下： + +```C++ +// 时间复杂度：O(n^2) +// 空间复杂度：O(1) +class Solution { +public: + int removeElement(vector
+
欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ + +> 在一个串中查找是否出现过另一个串，这是KMP的看家本领。 + +# 28. 实现 strStr() + +https://leetcode-cn.com/problems/implement-strstr/ + +实现 strStr() 函数。 + +给定一个 haystack 字符串和一个 needle 字符串，在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。 + +示例 1: +输入: haystack = "hello", needle = "ll" +输出: 2 + +示例 2: +输入: haystack = "aaaaa", needle = "bba" +输出: -1 + +说明: +当 needle 是空字符串时，我们应当返回什么值呢？这是一个在面试中很好的问题。 +对于本题而言，当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。 + + +# 思路 + +本题是KMP 经典题目。 + +以下文字如果看不进去，可以看我的B站视频： + +* [帮你把KMP算法学个通透！B站（理论篇）](https://www.bilibili.com/video/BV1PD4y1o7nd/) +* [帮你把KMP算法学个通透！（求next数组代码篇）](https://www.bilibili.com/video/BV1M5411j7Xx) + +KMP的经典思想就是:**当出现字符串不匹配时，可以记录一部分之前已经匹配的文本内容，利用这些信息避免从头再去做匹配。** + +本篇将以如下顺序来讲解KMP， + + +* 什么是KMP +* KMP有什么用 +* 什么是前缀表 +* 为什么一定要用前缀表 +* 如何计算前缀表 +* 前缀表与next数组 +* 使用next数组来匹配 +* 时间复杂度分析 +* 构造next数组 +* 使用next数组来做匹配 +* 前缀表统一减一 C++代码实现 +* 前缀表（不减一）C++实现 +* 总结 + + +读完本篇可以顺便把leetcode上28.实现strStr()题目做了。 + + +# 什么是KMP + +说到KMP，先说一下KMP这个名字是怎么来的，为什么叫做KMP呢。 + +因为是由这三位学者发明的：Knuth，Morris和Pratt，所以取了三位学者名字的首字母。所以叫做KMP + +# KMP有什么用 + +KMP主要应用在字符串匹配上。 + +KMP的主要思想是**当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。** + +所以如何记录已经匹配的文本内容，是KMP的重点，也是next数组肩负的重任。 + +其实KMP的代码不好理解，一些同学甚至直接把KMP代码的模板背下来。 + +没有彻底搞懂，懵懵懂懂就把代码背下来太容易忘了。 + +不仅面试的时候可能写不出来，如果面试官问：**next数组里的数字表示的是什么，为什么这么表示？** + +估计大多数候选人都是懵逼的。 + +下面Carl就带大家把KMP的精髓，next数组弄清楚。 + +# 什么是前缀表 + +写过KMP的同学，一定都写过next数组，那么这个next数组究竟是个啥呢？ + +next数组就是一个前缀表（prefix table）。 + +前缀表有什么作用呢？ + +**前缀表是用来回退的，它记录了模式串与主串(文本串)不匹配的时候，模式串应该从哪里开始重新匹配。** + +为了清楚的了解前缀表的来历，我们来举一个例子： + +要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。 + +请记住文本串和模式串的作用，对于理解下文很重要，要不然容易看懵。所以说三遍： + +要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。 + +要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。 + +要在文本串：aabaabaafa 中查找是否出现过一个模式串：aabaaf。 + +如动画所示： + + + +动画里，我特意把 子串`aa` 标记上了，这是有原因的，大家先注意一下，后面还会说道。 + +可以看出，文本串中第六个字符b 和 模式串的第六个字符f，不匹配了。如果暴力匹配，会发现不匹配，此时就要从头匹配了。 + +但如果使用前缀表，就不会从头匹配，而是从上次已经匹配的内容开始匹配，找到了模式串中第三个字符b继续开始匹配。 + +此时就要问了**前缀表是如何记录的呢？** + +首先要知道前缀表的任务是当前位置匹配失败，找到之前已经匹配上的位置，在重新匹配，此也意味着在某个字符失配时，前缀表会告诉你下一步匹配中，模式串应该跳到哪个位置。 + +那么什么是前缀表：**记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。** + +# 最长公共前后缀？ + +文章中字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**。 + +**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。 + +**正确理解什么是前缀什么是后缀很重要**! + +那么网上清一色都说 “kmp 最长公共前后缀” 又是什么回事呢？ + +我查了一遍 算法导论 和 算法4里KMP的章节，都没有提到 “最长公共前后缀”这个词，也不知道从哪里来了，我理解是用“最长相等前后缀” 更准确一些。 + +**因为前缀表要求的就是相同前后缀的长度。** + +而最长公共前后缀里面的“公共”，更像是说前缀和后缀公共的长度。这其实并不是前缀表所需要的。 + +所以字符串a的最长相等前后缀为0。 +字符串aa的最长相等前后缀为1。 +字符串aaa的最长相等前后缀为2。 +等等.....。 + + +# 为什么一定要用前缀表 + +这就是前缀表那为啥就能告诉我们 上次匹配的位置，并跳过去呢？ + +回顾一下，刚刚匹配的过程在下标5的地方遇到不匹配，模式串是指向f，如图： +
+
+
+然后就找到了下标2，指向b，继续匹配：如图：
+
+
+以下这句话，对于理解为什么使用前缀表可以告诉我们匹配失败之后跳到哪里重新匹配 非常重要！
+
+**下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀 和 后缀字符串是 子字符串aa ，因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面从新匹配就可以了。**
+
+所以前缀表具有告诉我们当前位置匹配失败，跳到之前已经匹配过的地方的能力。
+
+**很多介绍KMP的文章或者视频并没有把为什么要用前缀表？这个问题说清楚，而是直接默认使用前缀表。**
+
+# 如何计算前缀表
+
+接下来就要说一说怎么计算前缀表。
+
+如图：
+
+
+
+长度为前1个字符的子串`a`，最长相同前后缀的长度为0。（注意字符串的**前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串**；**后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串**。）
+
+
+长度为前2个字符的子串`aa`，最长相同前后缀的长度为1。
+
+
+长度为前3个字符的子串`aab`，最长相同前后缀的长度为0。
+
+以此类推：
+长度为前4个字符的子串`aaba`，最长相同前后缀的长度为1。
+长度为前5个字符的子串`aabaa`，最长相同前后缀的长度为2。
+长度为前6个字符的子串`aabaaf`，最长相同前后缀的长度为0。
+
+那么把求得的最长相同前后缀的长度就是对应前缀表的元素，如图：
+
+
+可以看出模式串与前缀表对应位置的数字表示的就是：**下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。**
+
+再来看一下如何利用 前缀表找到 当字符不匹配的时候应该指针应该移动的位置。如动画所示：
+
+
+
+找到的不匹配的位置， 那么此时我们要看它的前一个字符的前缀表的数值是多少。
+
+为什么要前一个字符的前缀表的数值呢，因为要找前面字符串的最长相同的前缀和后缀。
+
+所以要看前一位的 前缀表的数值。
+
+前一个字符的前缀表的数值是2， 所有把下标移动到下标2的位置继续比配。 可以再反复看一下上面的动画。
+
+最后就在文本串中找到了和模式串匹配的子串了。
+
+# 前缀表与next数组
+
+很多KMP算法的时间都是使用next数组来做回退操作，那么next数组与前缀表有什么关系呢？
+
+next数组就可以是前缀表，但是很多实现都是把前缀表统一减一（右移一位，初始位置为-1）之后作为next数组。
+
+为什么这么做呢，其实也是很多文章视频没有解释清楚的地方。
+
+其实**这并不涉及到KMP的原理，而是具体实现，next数组即可以就是前缀表，也可以是前缀表统一减一（右移一位，初始位置为-1）。**
+
+后面我会提供两种不同的实现代码，大家就明白了了。
+
+# 使用next数组来匹配
+
+**以下我们以前缀表统一减一之后的next数组来做演示**。
+
+有了next数组，就可以根据next数组来 匹配文本串s，和模式串t了。
+
+注意next数组是新前缀表（旧前缀表统一减一了）。
+
+匹配过程动画如下：
+
+
+
+# 时间复杂度分析
+
+其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。
+
+暴力的解法显而易见是O(n * m)，所以**KMP在字符串匹配中极大的提高的搜索的效率。**
+
+为了和力扣题目28.实现strStr保持一致，方便大家理解，以下文章统称haystack为文本串, needle为模式串。
+
+都知道使用KMP算法，一定要构造next数组。
+
+# 构造next数组
+
+我们定义一个函数getNext来构建next数组，函数参数为指向next数组的指针，和一个字符串。 代码如下：
+
+```
+void getNext(int* next, const string& s)
+```
+
+**构造next数组其实就是计算模式串s，前缀表的过程。** 主要有如下三步：
+
+1. 初始化
+2. 处理前后缀不相同的情况
+3. 处理前后缀相同的情况
+
+接下来我们详解详解一下。
+
+1. 初始化：
+
+定义两个指针i和j，j指向前缀起始位置，i指向后缀起始位置。
+
+然后还要对next数组进行初始化赋值，如下：
+
+```
+int j = -1;
+next[0] = j;
+```
+
+j 为什么要初始化为 -1呢，因为之前说过 前缀表要统一减一的操作仅仅是其中的一种实现，我们这里选择j初始化为-1，下文我还会给出j不初始化为-1的实现代码。
+
+next[i] 表示 i（包括i）之前最长相等的前后缀长度（其实就是j）
+
+所以初始化next[0] = j 。
+
+
+2. 处理前后缀不相同的情况
+
+
+因为j初始化为-1，那么i就从1开始，进行s[i] 与 s[j+1]的比较。
+
+所以遍历模式串s的循环下标i 要从 1开始，代码如下：
+
+```
+for(int i = 1; i < s.size(); i++) {
+```
+
+如果 s[i] 与 s[j+1]不相同，也就是遇到 前后缀末尾不相同的情况，就要向前回退。
+
+怎么回退呢？
+
+next[j]就是记录着j（包括j）之前的子串的相同前后缀的长度。
+
+那么 s[i] 与 s[j+1] 不相同，就要找 j+1前一个元素在next数组里的值（就是next[j]）。
+
+所以，处理前后缀不相同的情况代码如下：
+
+```
+while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
+ j = next[j]; // 向前回退
+}
+```
+
+3. 处理前后缀相同的情况
+
+如果s[i] 与 s[j + 1] 相同，那么就同时向后移动i 和j 说明找到了相同的前后缀，同时还要将j（前缀的长度）赋给next[i], 因为next[i]要记录相同前后缀的长度。
+
+代码如下：
+
+```
+if (s[i] == s[j + 1]) { // 找到相同的前后缀
+ j++;
+}
+next[i] = j;
+```
+
+最后整体构建next数组的函数代码如下：
+
+```C++
+void getNext(int* next, const string& s){
+ int j = -1;
+ next[0] = j;
+ for(int i = 1; i < s.size(); i++) { // 注意i从1开始
+ while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
+ j = next[j]; // 向前回退
+ }
+ if (s[i] == s[j + 1]) { // 找到相同的前后缀
+ j++;
+ }
+ next[i] = j; // 将j（前缀的长度）赋给next[i]
+ }
+}
+```
+
+
+代码构造next数组的逻辑流程动画如下：
+
+
+
+得到了next数组之后，就要用这个来做匹配了。
+
+# 使用next数组来做匹配
+
+在文本串s里 找是否出现过模式串t。
+
+定义两个下标j 指向模式串起始位置，i指向文本串起始位置。
+
+那么j初始值依然为-1，为什么呢？ **依然因为next数组里记录的起始位置为-1。**
+
+i就从0开始，遍历文本串，代码如下：
+
+```
+for (int i = 0; i < s.size(); i++)
+```
+
+接下来就是 s[i] 与 t[j + 1] （因为j从-1开始的） 进行比较。
+
+如果 s[i] 与 t[j + 1] 不相同，j就要从next数组里寻找下一个匹配的位置。
+
+代码如下：
+
+```
+while(j >= 0 && s[i] != t[j + 1]) {
+ j = next[j];
+}
+```
+
+如果 s[i] 与 t[j + 1] 相同，那么i 和 j 同时向后移动， 代码如下：
+
+```
+if (s[i] == t[j + 1]) {
+ j++; // i的增加在for循环里
+}
+```
+
+如何判断在文本串s里出现了模式串t呢，如果j指向了模式串t的末尾，那么就说明模式串t完全匹配文本串s里的某个子串了。
+
+本题要在文本串字符串中找出模式串出现的第一个位置 (从0开始)，所以返回当前在文本串匹配模式串的位置i 减去 模式串的长度，就是文本串字符串中出现模式串的第一个位置。
+
+代码如下：
+
+```
+if (j == (t.size() - 1) ) {
+ return (i - t.size() + 1);
+}
+```
+
+那么使用next数组，用模式串匹配文本串的整体代码如下：
+
+```C++
+int j = -1; // 因为next数组里记录的起始位置为-1
+for (int i = 0; i < s.size(); i++) { // 注意i就从0开始
+ while(j >= 0 && s[i] != t[j + 1]) { // 不匹配
+ j = next[j]; // j 寻找之前匹配的位置
+ }
+ if (s[i] == t[j + 1]) { // 匹配，j和i同时向后移动
+ j++; // i的增加在for循环里
+ }
+ if (j == (t.size() - 1) ) { // 文本串s里出现了模式串t
+ return (i - t.size() + 1);
+ }
+}
+```
+
+此时所有逻辑的代码都已经写出来了，力扣 28.实现strStr 题目的整体代码如下：
+
+# 前缀表统一减一 C++代码实现
+
+```C++
+class Solution {
+public:
+ void getNext(int* next, const string& s) {
+ int j = -1;
+ next[0] = j;
+ for(int i = 1; i < s.size(); i++) { // 注意i从1开始
+ while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
+ j = next[j]; // 向前回退
+ }
+ if (s[i] == s[j + 1]) { // 找到相同的前后缀
+ j++;
+ }
+ next[i] = j; // 将j（前缀的长度）赋给next[i]
+ }
+ }
+ int strStr(string haystack, string needle) {
+ if (needle.size() == 0) {
+ return 0;
+ }
+ int next[needle.size()];
+ getNext(next, needle);
+ int j = -1; // // 因为next数组里记录的起始位置为-1
+ for (int i = 0; i < haystack.size(); i++) { // 注意i就从0开始
+ while(j >= 0 && haystack[i] != needle[j + 1]) { // 不匹配
+ j = next[j]; // j 寻找之前匹配的位置
+ }
+ if (haystack[i] == needle[j + 1]) { // 匹配，j和i同时向后移动
+ j++; // i的增加在for循环里
+ }
+ if (j == (needle.size() - 1) ) { // 文本串s里出现了模式串t
+ return (i - needle.size() + 1);
+ }
+ }
+ return -1;
+ }
+};
+
+```
+
+# 前缀表（不减一）C++实现
+
+那么前缀表就不减一了，也不右移的，到底行不行呢？
+
+**行！**
+
+我之前说过，这仅仅是KMP算法实现上的问题，如果就直接使用前缀表可以换一种回退方式，找j=next[j-1] 来进行回退。
+
+主要就是j=next[x]这一步最为关键！
+
+我给出的getNext的实现为：（前缀表统一减一）
+
+```C++
+void getNext(int* next, const string& s) {
+ int j = -1;
+ next[0] = j;
+ for(int i = 1; i < s.size(); i++) { // 注意i从1开始
+ while (j >= 0 && s[i] != s[j + 1]) { // 前后缀不相同了
+ j = next[j]; // 向前回退
+ }
+ if (s[i] == s[j + 1]) { // 找到相同的前后缀
+ j++;
+ }
+ next[i] = j; // 将j（前缀的长度）赋给next[i]
+ }
+}
+
+```
+此时如果输入的模式串为aabaaf，对应的next为-1 0 -1 0 1 -1。
+
+这里j和next[0]初始化为-1，整个next数组是以 前缀表减一之后的效果来构建的。
+
+那么前缀表不减一来构建next数组，代码如下：
+
+```C++
+ void getNext(int* next, const string& s) {
+ int j = 0;
+ next[0] = 0;
+ for(int i = 1; i < s.size(); i++) {
+ while (j > 0 && s[i] != s[j]) { // j要保证大于0，因为下面有取j-1作为数组下标的操作
+ j = next[j - 1]; // 注意这里，是要找前一位的对应的回退位置了
+ }
+ if (s[i] == s[j]) {
+ j++;
+ }
+ next[i] = j;
+ }
+ }
+
+```
+
+此时如果输入的模式串为aabaaf，对应的next为 0 1 0 1 2 0，（其实这就是前缀表的数值了）。
+
+那么用这样的next数组也可以用来做匹配，代码要有所改动。
+
+实现代码如下：
+
+```C++
+class Solution {
+public:
+ void getNext(int* next, const string& s) {
+ int j = 0;
+ next[0] = 0;
+ for(int i = 1; i < s.size(); i++) {
+ while (j > 0 && s[i] != s[j]) {
+ j = next[j - 1];
+ }
+ if (s[i] == s[j]) {
+ j++;
+ }
+ next[i] = j;
+ }
+ }
+ int strStr(string haystack, string needle) {
+ if (needle.size() == 0) {
+ return 0;
+ }
+ int next[needle.size()];
+ getNext(next, needle);
+ int j = 0;
+ for (int i = 0; i < haystack.size(); i++) {
+ while(j > 0 && haystack[i] != needle[j]) {
+ j = next[j - 1];
+ }
+ if (haystack[i] == needle[j]) {
+ j++;
+ }
+ if (j == needle.size() ) {
+ return (i - needle.size() + 1);
+ }
+ }
+ return -1;
+ }
+};
+```
+
+# 总结
+
+我们介绍了什么是KMP，KMP可以解决什么问题，然后分析KMP算法里的next数组，知道了next数组就是前缀表，再分析为什么要是前缀表而不是什么其他表。
+
+接着从给出的模式串中，我们一步一步的推导出了前缀表，得出前缀表无论是统一减一还是不减一得到的next数组仅仅是kmp的实现方式的不同。
+
+其中还分析了KMP算法的时间复杂度，并且和暴力方法做了对比。
+
+然后先用前缀表统一减一得到的next数组，求得文本串s里是否出现过模式串t，并给出了具体分析代码。
+
+又给出了直接用前缀表作为next数组，来做匹配的实现代码。
+
+可以说把KMP的每一个细微的细节都扣了出来，毫无遮掩的展示给大家了！
+
+
+## 其他语言版本
+
+
+Java：
+
+```Java
+class Solution {
+ /**
+ * 基于窗口滑动的算法
+ *
+ * 时间复杂度：O(m*n)
+ * 空间复杂度：O(1)
+ * 注：n为haystack的长度，m为needle的长度
+ */
+ public int strStr(String haystack, String needle) {
+ int m = needle.length();
+ // 当 needle 是空字符串时我们应当返回 0
+ if (m == 0) {
+ return 0;
+ }
+ int n = haystack.length();
+ if (n < m) {
+ return -1;
+ }
+ int i = 0;
+ int j = 0;
+ while (i < n - m + 1) {
+ // 找到首字母相等
+ while (i < n && haystack.charAt(i) != needle.charAt(j)) {
+ i++;
+ }
+ if (i == n) {// 没有首字母相等的
+ return -1;
+ }
+ // 遍历后续字符，判断是否相等
+ i++;
+ j++;
+ while (i < n && j < m && haystack.charAt(i) == needle.charAt(j)) {
+ i++;
+ j++;
+ }
+ if (j == m) {// 找到
+ return i - j;
+ } else {// 未找到
+ i -= j - 1;
+ j = 0;
+ }
+ }
+ return -1;
+ }
+}
+```
+
+```java
+// 方法一
+class Solution {
+ public void getNext(int[] next, String s){
+ int j = -1;
+ next[0] = j;
+ for (int i = 1; i
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
+ 欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！
diff --git a/problems/0035.搜索插入位置.md b/problems/0035.搜索插入位置.md
new file mode 100644
index 00000000..1c5ad2c8
--- /dev/null
+++ b/problems/0035.搜索插入位置.md
@@ -0,0 +1,285 @@
+
diff --git a/problems/0037.解数独.md b/problems/0037.解数独.md
new file mode 100644
index 00000000..e43708b8
--- /dev/null
+++ b/problems/0037.解数独.md
@@ -0,0 +1,440 @@
+
diff --git a/problems/0039.组合总和.md b/problems/0039.组合总和.md
new file mode 100644
index 00000000..ba8128b5
--- /dev/null
+++ b/problems/0039.组合总和.md
@@ -0,0 +1,354 @@
+
diff --git a/problems/0040.组合总和II.md b/problems/0040.组合总和II.md
new file mode 100644
index 00000000..021bba94
--- /dev/null
+++ b/problems/0040.组合总和II.md
@@ -0,0 +1,398 @@
+
diff --git a/problems/0045.跳跃游戏II.md b/problems/0045.跳跃游戏II.md
new file mode 100644
index 00000000..4128da4c
--- /dev/null
+++ b/problems/0045.跳跃游戏II.md
@@ -0,0 +1,244 @@
+
diff --git a/problems/0046.全排列.md b/problems/0046.全排列.md
new file mode 100644
index 00000000..30c3374b
--- /dev/null
+++ b/problems/0046.全排列.md
@@ -0,0 +1,286 @@
+
diff --git a/problems/0047.全排列II.md b/problems/0047.全排列II.md
new file mode 100644
index 00000000..b4fb3470
--- /dev/null
+++ b/problems/0047.全排列II.md
@@ -0,0 +1,267 @@
+
diff --git a/problems/0051.N皇后.md b/problems/0051.N皇后.md
new file mode 100644
index 00000000..fd2c7d0f
--- /dev/null
+++ b/problems/0051.N皇后.md
@@ -0,0 +1,490 @@
+
diff --git a/problems/0053.最大子序和.md b/problems/0053.最大子序和.md
new file mode 100644
index 00000000..81e0b35a
--- /dev/null
+++ b/problems/0053.最大子序和.md
@@ -0,0 +1,217 @@
+
diff --git a/problems/0053.最大子序和（动态规划）.md b/problems/0053.最大子序和（动态规划）.md
new file mode 100644
index 00000000..dd0e513b
--- /dev/null
+++ b/problems/0053.最大子序和（动态规划）.md
@@ -0,0 +1,149 @@
+
diff --git a/problems/0055.跳跃游戏.md b/problems/0055.跳跃游戏.md
new file mode 100644
index 00000000..8618515e
--- /dev/null
+++ b/problems/0055.跳跃游戏.md
@@ -0,0 +1,164 @@
+
diff --git a/problems/0056.合并区间.md b/problems/0056.合并区间.md
new file mode 100644
index 00000000..d4ffc554
--- /dev/null
+++ b/problems/0056.合并区间.md
@@ -0,0 +1,232 @@
+
diff --git a/problems/0059.螺旋矩阵II.md b/problems/0059.螺旋矩阵II.md
new file mode 100644
index 00000000..6d8ec99c
--- /dev/null
+++ b/problems/0059.螺旋矩阵II.md
@@ -0,0 +1,315 @@
+
diff --git a/problems/0062.不同路径.md b/problems/0062.不同路径.md
new file mode 100644
index 00000000..50e70b3e
--- /dev/null
+++ b/problems/0062.不同路径.md
@@ -0,0 +1,336 @@
+
diff --git a/problems/0063.不同路径II.md b/problems/0063.不同路径II.md
new file mode 100644
index 00000000..a61ffd02
--- /dev/null
+++ b/problems/0063.不同路径II.md
@@ -0,0 +1,344 @@
+
diff --git a/problems/0070.爬楼梯.md b/problems/0070.爬楼梯.md
new file mode 100644
index 00000000..96899d37
--- /dev/null
+++ b/problems/0070.爬楼梯.md
@@ -0,0 +1,304 @@
+
diff --git a/problems/0070.爬楼梯完全背包版本.md b/problems/0070.爬楼梯完全背包版本.md
new file mode 100644
index 00000000..5c8270b6
--- /dev/null
+++ b/problems/0070.爬楼梯完全背包版本.md
@@ -0,0 +1,195 @@
+
diff --git a/problems/0072.编辑距离.md b/problems/0072.编辑距离.md
new file mode 100644
index 00000000..26f080fe
--- /dev/null
+++ b/problems/0072.编辑距离.md
@@ -0,0 +1,315 @@
+
diff --git a/problems/0077.组合.md b/problems/0077.组合.md
new file mode 100644
index 00000000..0b289a40
--- /dev/null
+++ b/problems/0077.组合.md
@@ -0,0 +1,443 @@
+
diff --git a/problems/0077.组合优化.md b/problems/0077.组合优化.md
new file mode 100644
index 00000000..d3e82f09
--- /dev/null
+++ b/problems/0077.组合优化.md
@@ -0,0 +1,252 @@
+
diff --git a/problems/0078.子集.md b/problems/0078.子集.md
new file mode 100644
index 00000000..0b2f3c09
--- /dev/null
+++ b/problems/0078.子集.md
@@ -0,0 +1,271 @@
+
diff --git a/problems/0090.子集II.md b/problems/0090.子集II.md
new file mode 100644
index 00000000..71aef5c7
--- /dev/null
+++ b/problems/0090.子集II.md
@@ -0,0 +1,291 @@
+
diff --git a/problems/0093.复原IP地址.md b/problems/0093.复原IP地址.md
new file mode 100644
index 00000000..40ad7684
--- /dev/null
+++ b/problems/0093.复原IP地址.md
@@ -0,0 +1,456 @@
+
diff --git a/problems/0096.不同的二叉搜索树.md b/problems/0096.不同的二叉搜索树.md
new file mode 100644
index 00000000..56f50d46
--- /dev/null
+++ b/problems/0096.不同的二叉搜索树.md
@@ -0,0 +1,237 @@
+
diff --git a/problems/0098.验证二叉搜索树.md b/problems/0098.验证二叉搜索树.md
new file mode 100644
index 00000000..b93d8cd5
--- /dev/null
+++ b/problems/0098.验证二叉搜索树.md
@@ -0,0 +1,477 @@
+
diff --git a/problems/0101.对称二叉树.md b/problems/0101.对称二叉树.md
new file mode 100644
index 00000000..9717588a
--- /dev/null
+++ b/problems/0101.对称二叉树.md
@@ -0,0 +1,592 @@
+
diff --git a/problems/0102.二叉树的层序遍历.md b/problems/0102.二叉树的层序遍历.md
new file mode 100644
index 00000000..2f56af52
--- /dev/null
+++ b/problems/0102.二叉树的层序遍历.md
@@ -0,0 +1,1689 @@
+