mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2026-02-02 18:39:09 +08:00
更新二叉树专题
This commit is contained in:
222
problems/0104.二叉树的最大深度.md
Normal file
222
problems/0104.二叉树的最大深度.md
Normal file
@@ -0,0 +1,222 @@
|
||||
|
||||
|
||||
看完本篇可以一起做了如下两道题目:
|
||||
* 104.二叉树的最大深度
|
||||
* 559.N叉树的最大深度
|
||||
|
||||
## 104.二叉树的最大深度
|
||||
|
||||
题目地址:https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
|
||||
|
||||
给定一个二叉树,找出其最大深度。
|
||||
|
||||
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
|
||||
|
||||
说明: 叶子节点是指没有子节点的节点。
|
||||
|
||||
示例:
|
||||
给定二叉树 [3,9,20,null,null,15,7],
|
||||
|
||||

|
||||
|
||||
返回它的最大深度 3 。
|
||||
|
||||
### 递归法
|
||||
|
||||
本题其实也要后序遍历(左右中),依然是因为要通过递归函数的返回值做计算树的高度。
|
||||
|
||||
按照递归三部曲,来看看如何来写。
|
||||
|
||||
1. 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
|
||||
|
||||
代码如下:
|
||||
```
|
||||
int getDepth(TreeNode* node)
|
||||
```
|
||||
|
||||
2. 确定终止条件:如果为空节点的话,就返回0,表示高度为0。
|
||||
|
||||
代码如下:
|
||||
```
|
||||
if (node == NULL) return 0;
|
||||
```
|
||||
|
||||
3. 确定单层递归的逻辑:先求它的左子树的深度,再求的右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
|
||||
|
||||
代码如下:
|
||||
|
||||
```
|
||||
int leftDepth = getDepth(node->left); // 左
|
||||
int rightDepth = getDepth(node->right); // 右
|
||||
int depth = 1 + max(leftDepth, rightDepth); // 中
|
||||
return depth;
|
||||
```
|
||||
|
||||
所以整体C++代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int getDepth(TreeNode* node) {
|
||||
if (node == NULL) return 0;
|
||||
int leftDepth = getDepth(node->left); // 左
|
||||
int rightDepth = getDepth(node->right); // 右
|
||||
int depth = 1 + max(leftDepth, rightDepth); // 中
|
||||
return depth;
|
||||
}
|
||||
int maxDepth(TreeNode* root) {
|
||||
return getDepth(root);
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
代码精简之后C++代码如下:
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int maxDepth(TreeNode* root) {
|
||||
if (root == NULL) return 0;
|
||||
return 1 + max(maxDepth(root->left), maxDepth(root->right));
|
||||
}
|
||||
};
|
||||
|
||||
```
|
||||
|
||||
**精简之后的代码根本看不出是哪种遍历方式,也看不出递归三部曲的步骤,所以如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。**
|
||||
|
||||
|
||||
### 迭代法
|
||||
|
||||
使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
|
||||
|
||||
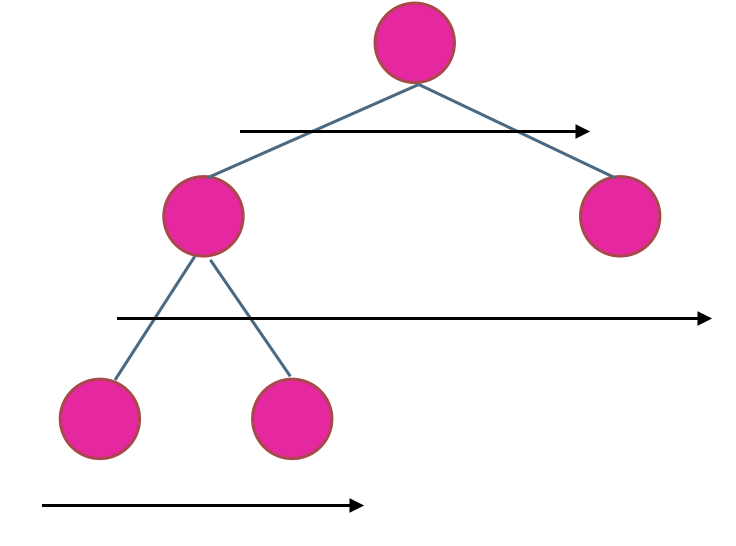
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
|
||||
|
||||
|
||||
|
||||
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
|
||||
|
||||
如果对层序遍历还不清楚的话,可以看这篇:[二叉树:层序遍历登场!](https://mp.weixin.qq.com/s/Gb3BjakIKGNpup2jYtTzog)
|
||||
|
||||
C++代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int maxDepth(TreeNode* root) {
|
||||
if (root == NULL) return 0;
|
||||
int depth = 0;
|
||||
queue<TreeNode*> que;
|
||||
que.push(root);
|
||||
while(!que.empty()) {
|
||||
int size = que.size();
|
||||
depth++; // 记录深度
|
||||
for (int i = 0; i < size; i++) {
|
||||
TreeNode* node = que.front();
|
||||
que.pop();
|
||||
if (node->left) que.push(node->left);
|
||||
if (node->right) que.push(node->right);
|
||||
}
|
||||
}
|
||||
return depth;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
那么我们可以顺便解决一下N叉树的最大深度问题
|
||||
|
||||
## 559.N叉树的最大深度
|
||||
|
||||
题目地址:https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/
|
||||
|
||||
给定一个 N 叉树,找到其最大深度。
|
||||
|
||||
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
|
||||
|
||||
例如,给定一个 3叉树 :
|
||||
|
||||

|
||||
|
||||
我们应返回其最大深度,3。
|
||||
|
||||
思路:
|
||||
|
||||
依然可以提供递归法和迭代法,来解决这个问题,思路是和二叉树思路一样的,直接给出代码如下:
|
||||
|
||||
### 递归法
|
||||
|
||||
C++代码:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int maxDepth(Node* root) {
|
||||
if (root == 0) return 0;
|
||||
int depth = 0;
|
||||
for (int i = 0; i < root->children.size(); i++) {
|
||||
depth = max (depth, maxDepth(root->children[i]));
|
||||
}
|
||||
return depth + 1;
|
||||
}
|
||||
};
|
||||
```
|
||||
### 迭代法
|
||||
|
||||
依然是层序遍历,代码如下:
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int maxDepth(Node* root) {
|
||||
queue<Node*> que;
|
||||
if (root != NULL) que.push(root);
|
||||
int depth = 0;
|
||||
while (!que.empty()) {
|
||||
int size = que.size();
|
||||
depth++; // 记录深度
|
||||
for (int i = 0; i < size; i++) {
|
||||
Node* node = que.front();
|
||||
que.pop();
|
||||
for (int j = 0; j < node->children.size(); j++) {
|
||||
if (node->children[j]) que.push(node->children[j]);
|
||||
}
|
||||
}
|
||||
}
|
||||
return depth;
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
使用栈来模拟后序遍历依然可以
|
||||
|
||||
```C++
|
||||
class Solution {
|
||||
public:
|
||||
int maxDepth(TreeNode* root) {
|
||||
stack<TreeNode*> st;
|
||||
if (root != NULL) st.push(root);
|
||||
int depth = 0;
|
||||
int result = 0;
|
||||
while (!st.empty()) {
|
||||
TreeNode* node = st.top();
|
||||
if (node != NULL) {
|
||||
st.pop();
|
||||
st.push(node); // 中
|
||||
st.push(NULL);
|
||||
depth++;
|
||||
if (node->right) st.push(node->right); // 右
|
||||
if (node->left) st.push(node->left); // 左
|
||||
|
||||
} else {
|
||||
st.pop();
|
||||
node = st.top();
|
||||
st.pop();
|
||||
depth--;
|
||||
}
|
||||
result = result > depth ? result : depth;
|
||||
}
|
||||
return result;
|
||||
|
||||
}
|
||||
};
|
||||
```
|
||||
|
||||
Reference in New Issue
Block a user