Update

problems/kamacoder/0047.参会dijkstra朴素.md

@@ -150,7 +150,7 @@ minDist数组数值初始化为int最大值。
 更新 minDist数组，即：源点（节点1） 到 节点2 和 节点3的距离。 
 
 * 源点到节点2的最短距离为1，小于原minDist[2]的数值max，更新minDist[2] = 1 
-* 源点到节点3的最短距离为4，小于原minDist[3]的数值max，更新minDist[4] = 4 
+* 源点到节点3的最短距离为4，小于原minDist[3]的数值max，更新minDist[3] = 4 
 
 可能有录友问：为啥和 minDist[2] 比较？
 

problems/kamacoder/0053.寻宝-prim.md

@@ -176,7 +176,7 @@ minDist 数组 里的数值初始化为 最大数，因为本题 节点距离不
 
 所有非生成树的节点距离 最小生成树（节点1、节点2、节点3 ）的距离都已经跟新了 。 
 
-* 节点 4 和 节点 3的距离为 1，和原先的距离值 2 小，所以更新minDist[3]为1。  
+* 节点 4 和 节点 3的距离为 1，和原先的距离值 2 小，所以更新minDist[4]为1。  
 
 上面为什么我们只比较 节点4 和 节点3 的距离呢？ 
 
@@ -213,7 +213,7 @@ minDist 数组 里的数值初始化为 最大数，因为本题 节点距离不
 
 minDist数组已经更新了 所有非生成树的节点距离 最小生成树（节点1、节点2、节点3、节点4 ）的距离 。 
 
-* 节点 5 和 节点 4的距离为 1，和原先的距离值 2 小，所以更新minDist[4]为1。  
+* 节点 5 和 节点 4的距离为 1，和原先的距离值 2 小，所以更新minDist[5]为1。  
 
 ### 6 
 

problems/kamacoder/0095.城市间货物运输II.md

@@ -247,6 +247,61 @@ int main() {
 
 ### Python
 
+```python 
+import sys
+
+def main():
+    input = sys.stdin.read
+    data = input().split()
+    index = 0
+    
+    n = int(data[index])
+    index += 1
+    m = int(data[index])
+    index += 1
+    
+    grid = []
+    for i in range(m):
+        p1 = int(data[index])
+        index += 1
+        p2 = int(data[index])
+        index += 1
+        val = int(data[index])
+        index += 1
+        # p1 指向 p2，权值为 val
+        grid.append([p1, p2, val])
+
+    start = 1  # 起点
+    end = n    # 终点
+
+    minDist = [float('inf')] * (n + 1)
+    minDist[start] = 0
+    flag = False
+
+    for i in range(1, n + 1):  # 这里我们松弛n次，最后一次判断负权回路
+        for side in grid:
+            from_node = side[0]
+            to = side[1]
+            price = side[2]
+            if i < n:
+                if minDist[from_node] != float('inf') and minDist[to] > minDist[from_node] + price:
+                    minDist[to] = minDist[from_node] + price
+            else:  # 多加一次松弛判断负权回路
+                if minDist[from_node] != float('inf') and minDist[to] > minDist[from_node] + price:
+                    flag = True
+
+    if flag:
+        print("circle")
+    elif minDist[end] == float('inf'):
+        print("unconnected")
+    else:
+        print(minDist[end])
+
+if __name__ == "__main__":
+    main()
+
+```
+
 ### Go
 
 ### Rust

problems/kamacoder/0099.岛屿的数量广搜.md

@@ -192,50 +192,6 @@ int main() {
 
 ```java
 
-import java.util.Scanner;
-
-public class Main {
-    static int[][] dir = { {0, 1}, {1, 0}, {-1, 0}, {0, -1} }; // 四个方向
-
-    public static void dfs(int[][] grid, boolean[][] visited, int x, int y) {
-        for (int i = 0; i < 4; i++) {
-            int nextx = x + dir[i][0];
-            int nexty = y + dir[i][1];
-            if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) continue;  // 越界了，直接跳过
-            if (!visited[nextx][nexty] && grid[nextx][nexty] == 1) { // 没有访问过的 同时 是陆地的
-                visited[nextx][nexty] = true;
-                dfs(grid, visited, nextx, nexty);
-            }
-        }
-    }
-
-    public static void main(String[] args) {
-        Scanner scanner = new Scanner(System.in);
-        int n = scanner.nextInt();
-        int m = scanner.nextInt();
-        int[][] grid = new int[n][m];
-        for (int i = 0; i < n; i++) {
-            for (int j = 0; j < m; j++) {
-                grid[i][j] = scanner.nextInt();
-            }
-        }
-
-        boolean[][] visited = new boolean[n][m];
-
-        int result = 0;
-        for (int i = 0; i < n; i++) {
-            for (int j = 0; j < m; j++) {
-                if (!visited[i][j] && grid[i][j] == 1) {
-                    visited[i][j] = true;
-                    result++; // 遇到没访问过的陆地，+1
-                    dfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
-                }
-            }
-        }
-
-        System.out.println(result);
-    }
-}
 
 
 
@@ -246,32 +202,6 @@ public class Main {
 
 ```python
 
-def dfs(grid, visited, x, y):
-    dir = [(0, 1), (1, 0), (-1, 0), (0, -1)]  # 四个方向
-    for d in dir:
-        nextx, nexty = x + d[0], y + d[1]
-        if 0 <= nextx < len(grid) and 0 <= nexty < len(grid[0]):
-            if not visited[nextx][nexty] and grid[nextx][nexty] == 1:  # 没有访问过的 同时 是陆地的
-                visited[nextx][nexty] = True
-                dfs(grid, visited, nextx, nexty)
-
-def main():
-    n, m = map(int, input().split())
-    grid = [list(map(int, input().split())) for _ in range(n)]
-    visited = [[False] * m for _ in range(n)]
-
-    result = 0
-    for i in range(n):
-        for j in range(m):
-            if not visited[i][j] and grid[i][j] == 1:
-                visited[i][j] = True
-                result += 1  # 遇到没访问过的陆地，+1
-                dfs(grid, visited, i, j)  # 将与其链接的陆地都标记上 True
-
-    print(result)
-
-if __name__ == "__main__":
-    main()
 
 
 

problems/kamacoder/0104.建造最大岛屿.md

@@ -17,7 +17,7 @@
 
 输出描述：
 
-输出一个整数，表示最大的岛屿面积。如果矩阵中不存在岛屿，则输出 0。
+输出一个整数，表示最大的岛屿面积。
 
 输入示例：
 

problems/kamacoder/0109.冗余连接II.md

@@ -7,16 +7,21 @@
 
 题目描述
 
-有向树指满足以下条件的有向图。该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。
+有一种有向树,该树只有一个根节点，所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点，而根节点没有父节点。有向树拥有 n 个节点和 n - 1 条边。如图： 
 
+<img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20240827152106.png" alt="" width="50%" />
 
-输入一个有向图，该图由一个有着 n 个节点（节点编号 从 1 到 n），n 条边，请返回一条可以删除的边，使得删除该条边之后该有向图可以被当作一颗有向树。
+现在有一个有向图，有向图是在有向树中的两个没有直接链接的节点中间添加一条有向边。如图：
+
+<img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20240827152134.png" alt="" width="50%" />
+
+输入一个有向图，该图由一个有着 n 个节点(节点编号 从 1 到 n)，n 条边，请返回一条可以删除的边，使得删除该条边之后该有向图可以被当作一颗有向树。
 
 输入描述
 
 第一行输入一个整数 N，表示有向图中节点和边的个数。
 
-后续 N 行，每行输入两个整数 s 和 t，代表 s 节点有一条连接 t 节点的单向边
+后续 N 行，每行输入两个整数 s 和 t，代表这是 s 节点连接并指向 t 节点的单向边
 
 输出描述
 
@@ -37,7 +42,7 @@
 
 提示信息 
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527112633.png) 
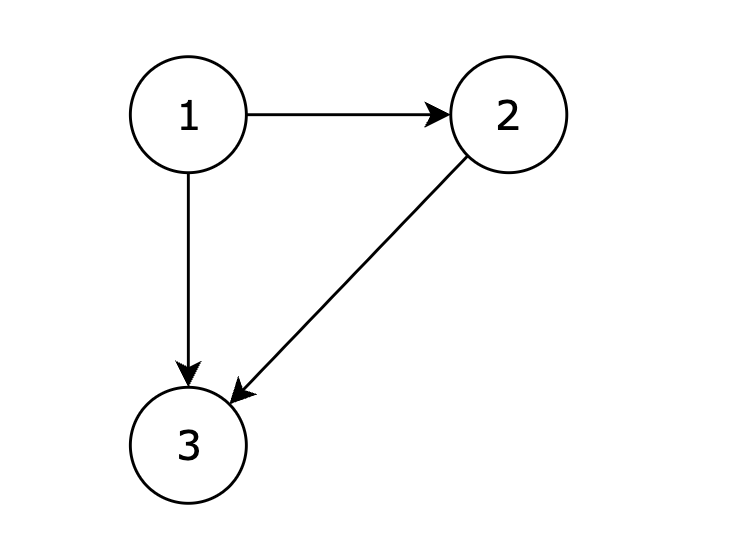
+<img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20240527112633.png" alt="" width="50%" />
 
 在删除 2 3 后有向图可以变为一棵合法的有向树，所以输出 2 3
 

problems/kamacoder/0153.权值优势路径计数.md

@@ -0,0 +1,95 @@
+
+
+# 权值优势路径计数 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1231)
+
+1、构建二叉树：首先根据层序遍历的序列构建二叉树。这可以通过使用队列来实现，队列中存储当前节点及其索引，确保可以正确地将子节点添加到父节点下。
+
+2、路径遍历：使用深度优先搜索（DFS）遍历所有从根到叶子的路径。在遍历过程中，维护一个计数器跟踪当前路径中权值为 1 和权值为 0 的节点的数量。
+
+3、计数满足条件的路径：每当到达一个叶子节点时，检查当前路径的权值 1 的节点数量是否比权值 0 的节点数量多 1。如果满足，递增一个全局计数器。
+
+
+```CPP 
+
+#include <iostream>
+#include <vector>
+#include <queue>
+
+using namespace std;
+
+struct TreeNode {
+    int val;
+    TreeNode *left, *right;
+    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
+};
+
+// DFS遍历二叉树，并计算满足条件的路径数量
+void countPaths(TreeNode* node, int count1, int count0, int& result) {
+    if (!node) return;
+
+    // 更新当前路径中1和0的数量
+    node->val == 1 ? count1++ : count0++;
+
+    // 检查当前节点是否为叶子节点
+    if (!node->left && !node->right) {
+        // 检查1的数量是否比0的数量多1
+        if (count1 == count0 + 1) {
+            result++;
+        }
+        return;
+    }
+
+    // 递归访问左右子节点
+    countPaths(node->left, count1, count0, result);
+    countPaths(node->right, count1, count0, result);
+}
+
+int main() {
+    int N;
+    cin >> N;
+
+    vector<int> nums(N);
+    for (int i = 0; i < N; ++i) {
+        cin >> nums[i];
+    }
+
+    if (nums.empty()) {
+        cout << 0 << endl;
+        return 0;
+    }
+
+    // 根据层序遍历的输入构建二叉树
+    queue<TreeNode*> q;
+    TreeNode* root = new TreeNode(nums[0]);
+    q.push(root);
+    int index = 1;
+
+    while (!q.empty() && index < N) {
+        TreeNode* node = q.front();
+        q.pop();
+
+        if (index < N && nums[index] != -1) {
+            node->left = new TreeNode(nums[index]);
+            q.push(node->left);
+        }
+        index++;
+
+        if (index < N && nums[index] != -1) {
+            node->right = new TreeNode(nums[index]);
+            q.push(node->right);
+        }
+        index++;
+    }
+
+    // 计算满足条件的路径数
+    int result = 0;
+    countPaths(root, 0, 0, result);
+
+    cout << result << endl;
+
+    return 0;
+}
+
+```

problems/kamacoder/0154.序列中位数.md

@@ -0,0 +1,68 @@
+
+# 序列中位数 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1232)
+
+注意给的数组默认不是有序的！ 
+
+模拟题，排序之后，取中位数，然后按照b数组 删 a数组中元素，再取中位数。
+
+```CPP 
+#include<bits/stdc++.h>
+using namespace std; 
+
+// 计算并返回中位数
+double findMedian(vector<int>& nums) {
+    int n = nums.size();
+    if (n % 2 == 1) {
+        return nums[n / 2]; // 奇数长度，返回中间的元素
+    } else {
+        // 偶数长度，返回中间两个元素的平均值
+        return (nums[n / 2] + nums[n / 2 - 1]) / 2.0;
+    }
+}
+
+
+int main(){
+    int t;
+    cin >> t;
+    while(t--){
+        int n;
+        cin>> n;
+        vector<int> a(n);
+        vector<int> b(n - 1);
+        for(int i = 0; i < n; i++){
+            cin >> a[i];
+        }
+        for(int i = 0; i < n - 1; i++){
+            cin >> b[i];
+        }
+        vector<int> nums = a;
+        vector<double> answers; 
+        
+        sort(nums.begin(), nums.end());
+      
+        // 把中位数放进结果集
+        answers.push_back(findMedian(nums));
+
+        for(int i = 0; i < n - 1; i++){ 
+            
+            int target = a[b[i]];
+            // 删除目标值
+            nums.erase(find(nums.begin(), nums.end(), target));
+            // 把中位数放进结果集
+            answers.push_back(findMedian(nums));
+
+        }
+
+        for(auto answer : answers){  
+            // 判断是否是整数
+            if(answer == (int)answer) printf("%d ", (int)answer);
+            else printf("%.1f ", answer);
+        }
+        cout << endl;
+    }
+
+}
+
+```

problems/kamacoder/0155.最小化频率的删除代价.md

@@ -0,0 +1,106 @@
+
+# 最小化频率的删除代价 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1233)
+
+计数和排序：
+
+* 使用 map 或 unordered_map 对数组 a 中每个元素出现的次数进行统计。
+* 将统计结果存入一个 vector<pair<int, int>>，其中 pair 的第一个元素是元素的出现次数，第二个元素是元素本身。
+* 按出现次数从大到小排序这个 vector。
+
+确定最小 f(a)：
+
+* 从最大出现次数开始尝试减少 f(a)。为此，从最高频次的元素开始逐步向下考虑较少出现的元素，计算达到更低 f(a) 所需删除的元素数量。
+* 使用一个累加器 count 来记录需要删除的元素数量，直到这个数量超过允许的最大删除数量 k 或恰好等于 k。在此过程中，尽量使 f(a) 达到最小。
+
+计算达到 f(a) 的代价：
+
+* 计算完成后，需要确定达到最小 f(a) 的确切代价。首先，为每个元素确定在不超过 k 的前提下可以删除的最大数量，以使得 f(a) 最小。
+* 对于每个元素，如果它的数量超过了新的 f(a)，则计算减少到 f(a) 所需删除的具体元素数，记录下来。
+
+计算具体删除代价：
+
+* 遍历原数组，对于每个需要删除的元素，根据其位置累加删除代价。每删除一个元素，相应地减少其在删除列表中的计数。当某元素需要删除的数量减至 0 时，从删除列表中移除该元素。
+
+
+```CPP 
+
+#include <iostream>
+#include <vector>
+#include <unordered_map>
+#include <algorithm>
+
+using namespace std;
+
+int main() {
+    int n, k;
+    cin >> n >> k;
+
+    vector<int> a(n);
+    for (int i = 0; i < n; ++i) {
+        cin >> a[i];
+    }
+
+    unordered_map<int, int> umap;  // 使用map来统计每个元素的出现频率
+    for (int i = 0; i < n; ++i) {
+        umap[a[i]]++;  // 统计每个元素的出现次数
+    }
+
+    vector<pair<int, int>> table;
+    for (auto& pair : umap) {
+        table.push_back({pair.second, pair.first});  // 将元素和其频率作为一个pair放入table中
+    }
+
+    sort(table.begin(), table.end(), greater<>());  // 将table按照频率从大到小排序
+
+    int count = 0;  // 用来计算已经删除的元素总数
+    int minVal = table[0].first;  // 从最高频率开始
+    for (int i = 0; i < table.size(); ++i) {
+        int freq = table[i].first;
+        count += (minVal - freq) * i;  // 累加删除元素的代价
+        if (count > k) break;  // 如果超过了k，停止循环
+        else if (count == k) {
+            minVal = freq;
+            break;
+        } else minVal = freq;
+    }
+    if (count < k) {
+        int addDel = (k - count) / table.size();  // 如果删除的代价还没达到k，计算还可以进一步减少的频率
+        minVal -= addDel;  // 减少相应的频率
+    }
+
+    if (minVal < 0) {
+        minVal = 0;  // 确保最小频率值不小于0
+    }
+
+    unordered_map<int, int> deleteList;  // 用来存储需要删除的元素及其数量
+    for (auto& elem : table) {
+        int num = elem.first;
+        int ind = elem.second;
+        if (num > minVal) {
+            deleteList[ind] = num - minVal;  // 如果元素频率大于最小值，计算需要删除的数量
+        } else {
+            break;
+        }
+    }
+
+    int cost = 0;  // 计算总的删除代价
+    for (int i = 0; i < n; ++i) {
+        if (deleteList.find(a[i]) != deleteList.end()) {
+            cost += i + 1;  // 删除的代价是元素的索引+1
+            deleteList[a[i]]--;  // 删除一个元素
+            if (deleteList[a[i]] == 0) {
+                deleteList.erase(a[i]);  // 如果元素已经全部删除，从列表中移除
+                if (deleteList.empty()) {
+                    break;  // 如果没有元素需要删除了，结束循环
+                }
+            }
+        }
+    }
+
+    cout << minVal << " " << cost << endl;
+    return 0;
+}
+
+```

problems/kamacoder/0156.勇敢牛牛战斗序列.md

@@ -0,0 +1,68 @@
+
+# 勇敢牛牛战斗序列
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1234)
+
+贪心思路，对数组从小到大排序之后，先取最右边，再取最左边，循环反复。
+
+```CPP 
+#include<bits/stdc++.h>
+
+using namespace std;
+
+int main() {
+    int n;
+    cin >> n;
+    vector<int> a(n); // 使用 vector 存储整数数组
+    for (int i = 0; i < n; i++) {
+        cin >> a[i]; // 读取数组
+    }
+    sort(a.begin(), a.end()); // 对数组进行排序
+
+    long long ans = 0; // 使用 long long 存储结果，以防溢出
+    int cur = 0;
+    int left = 0, right = n - 1;
+    while (left <= right) {
+        if (cur < a[right]) {
+            ans += a[right] - cur;
+        }
+        cur = a[left];
+        right--;
+        left++;
+    }
+    cout << ans << endl; // 输出结果
+    return 0;
+} 
+```
+
+
+
+```Java
+import java.util.Arrays;
+import java.util.Scanner;
+
+public class Main {
+
+    public static void main(String[] args) {
+        Scanner sc = new Scanner(System.in);
+        int n = sc.nextInt();
+        int[] a = new int[n];
+        for (int i = 0; i < n; i++) {
+            a[i] = sc.nextInt();
+        }
+        Arrays.sort(a);
+        long ans = 0;
+        int cur = 0;
+        int left = 0, right = a.length - 1;
+        while (left <= right) {
+            if (cur < a[right]) {
+                ans = ans + a[right] - cur;
+            }
+            cur = a[left];
+            right--;
+            left++;
+        }
+        System.out.println(ans);
+    }
+}
+```

problems/kamacoder/0157.最大化密码复杂度.md

@@ -0,0 +1,59 @@
+
+# 最大化密码复杂度 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1235)
+
+注意**边界处理**，对于字符串的首尾位置，需要特别处理，因为它们只有一个相邻字符。
+* 遍历字符串 s，寻找 '?' 字符。
+* 对于每个 '?' 字符，选择一个字符填充，使其与前后字符都不同。这样做的目的是最大化密码的复杂度，即尽可能使相邻的字符不同。
+* 如果 '?' 是第一个或最后一个字符，或者无法找到与前后都不同的字符，选择与前一个或后一个字符不同的字符。
+
+
+```CPP 
+#include <iostream>
+#include <vector>
+#include <algorithm>
+
+using namespace std;
+
+int main() {
+    int n, m;
+    string s;
+    cin >> n >> m >> s;
+
+    if (n == 1) {
+        cout << 0 << endl;
+        return 0;
+    }
+
+    // 统一处理包括左右字符的情况
+    for (int i = 0; i < n; ++i) {
+        if (s[i] == '?') {
+            bool found = false;
+            for (char j = 'a'; j < 'a' + m; ++j) {
+                // 避免第一个字符 和 最后一个字符，因为两个字符只有一个相邻字符，没有左右相邻字符
+                if ((i == 0 || s[i - 1] != j) && (i == n - 1 || s[i + 1] != j)) {
+                    s[i] = j;
+                    found = true;
+                    break;
+                }
+            }
+            // 如果没有找到合适的字符，就和附近字符保持一致
+            if (!found) {
+                if (i > 0)  s[i] = s[i - 1];
+                 else  s[i] = s[i + 1];
+            }
+        }
+    }
+
+    // 计算结果
+    int result = 0;
+    for (int i = 0; i < n - 1; ++i) {
+        if (s[i] != s[i + 1]) result++;
+    }
+
+    cout << result << endl;
+    return 0;
+}
+
+```

problems/kamacoder/0158.同余方程.md

@@ -0,0 +1,50 @@
+
+# 同余方程 
+
+题目链接：https://kamacoder.com/problempage.php?pid=1236
+
+我们需要求出满足以下条件的最小正整数 x：`ax≡1 (mod b)`
+
+这意味着我们需要找到 x 使得 ax 除以 b 的余数是 1。这个问题实际上是一个典型的 模反元素 问题。
+
+解题思路：
+
+* 为了求出最小的 x，我们可以使用 扩展欧几里得算法 来求出 a 对模 b 的逆元。
+* 这个算法能够求解 ax + by = gcd(a, b) 的一组整数解 (x, y)，而在 gcd(a, b) = 1 的情况下，x 即为所求的模逆元。
+* 扩展欧几里得算法：扩展欧几里得算法可以通过递归或者迭代的方式实现。
+
+下面给出C++代码实现：
+
+```CPP
+#include <iostream>
+using namespace std;
+
+// 扩展欧几里得：计算 ax + by = gcd(a, b) 的解
+long long extended_gcd(long long a, long long b, long long &x, long long &y) {
+    if (b == 0) {
+        x = 1;
+        y = 0;
+        return a;
+    }
+    long long x1, y1;
+    long long gcd = extended_gcd(b, a % b, x1, y1);
+    x = y1;
+    y = x1 - (a / b) * y1;
+    return gcd;
+}
+
+int main() {
+    long long a, b;
+    cin >> a >> b;
+
+    long long x, y;
+    long long gcd = extended_gcd(a, b, x, y);
+
+    // 由于我们只需要模 b 的正整数解，所以我们要保证 x 是正数
+    x = (x % b + b) % b;
+
+    cout << x << endl;
+
+    return 0;
+}
+```

problems/kamacoder/0159.大整数乘法.md

@@ -0,0 +1,62 @@
+
+# 大整数乘法 
+
+题目链接：https://kamacoder.com/problempage.php?pid=1237
+
+思路：
+
+我们可以使用模拟手算乘法的方法，即「逐位相乘累加」，对于每一位的乘法结果，我们将其加到相应的结果位置上。最终将累加的结果输出。
+
+具体步骤：
+
+* 初始化结果数组：结果数组的长度应该是两个数字长度之和，因为最大长度的结果不会超过这个长度。
+* 逐位相乘：从右往左遍历两个字符串的每一位，逐位相乘，并加到结果数组的相应位置。
+* 处理进位：在每一步累加之后处理进位，保证每个位置的值小于10。
+
+将结果数组转化为字符串：从结果数组的最高位开始，忽略前导零，然后将数组转化为字符串。 
+
+```CPP 
+#include <iostream>
+#include <vector>
+#include <string>
+
+using namespace std;
+
+string multiply(string num1, string num2) {
+    int len1 = num1.size();
+    int len2 = num2.size();
+    vector<int> result(len1 + len2, 0);
+
+    // 逐位相乘
+    for (int i = len1 - 1; i >= 0; i--) {
+        for (int j = len2 - 1; j >= 0; j--) {
+            int mul = (num1[i] - '0') * (num2[j] - '0');
+            int sum = mul + result[i + j + 1];
+
+            result[i + j + 1] = sum % 10;
+            result[i + j] += sum / 10;
+        }
+    }
+
+    // 将结果转换为字符串，跳过前导零
+    string product;
+    for (int num : result) {
+        if (!(product.empty() && num == 0)) {  // 跳过前导零
+            product.push_back(num + '0');
+        }
+    }
+
+    return product.empty() ? "0" : product;
+}
+
+int main() {
+    string num1, num2;
+    cin >> num1 >> num2;
+
+    string result = multiply(num1, num2);
+    cout << result << endl;
+
+    return 0;
+}
+ 
+```

problems/kamacoder/0160.二维平面上的折线段.md

@@ -0,0 +1,88 @@
+
+# 二维平面上的折线段 
+
+题目链接：https://kamacoder.com/problempage.php?pid=1238
+
+这个问题要求我们在一条折线段上，根据移动的固定距离 s 进行标记点的计算。
+
+为了实现这一点，我们需要对折线段进行分段处理，并根据每段的长度来确定标记点的位置。
+
+解题思路：
+
+1. 输入与初步处理：
+    * 首先，读取所有点的坐标。
+    * 计算每一段折线的长度，并逐段累积总长度。
+2. 确定标记点：
+    * 从起点开始，每次沿着折线段前进 s 的距离，直到到达终点。
+    * 对于每个标记点，根据当前段的起点和终点，计算出该点的精确坐标。
+3. 输出所有标记点的坐标，格式为 x, y。
+
+```CPP 
+
+#include <iostream>
+#include <vector>
+#include <cmath>
+#include <iomanip>
+
+using namespace std;
+
+// 定义一个点的结构体
+struct Point {
+    double x, y;
+};
+
+// 计算两点之间的距离
+double distance(const Point& a, const Point& b) {
+    return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
+}
+
+int main() {
+    int n;
+    cin >> n;
+
+    vector<Point> points(n);
+    for (int i = 0; i < n; i++) {
+        cin >> points[i].x >> points[i].y;
+    }
+
+    double s;
+    cin >> s;
+
+    double total_length = 0.0;
+    vector<double> segment_lengths(n - 1);
+
+    // 计算每段长度和总长度
+    for (int i = 0; i < n - 1; i++) {
+        segment_lengths[i] = distance(points[i], points[i + 1]);
+        total_length += segment_lengths[i];
+    }
+
+    // 从起点开始标记
+    Point current_point = points[0];
+    double accumulated_distance = 0.0;
+
+    cout << fixed << setprecision(5);
+    cout << current_point.x << ", " << current_point.y << endl;
+
+    while (accumulated_distance + s <= total_length) {
+        accumulated_distance += s;
+        double remaining_distance = accumulated_distance;
+
+        for (int i = 0; i < n - 1; i++) {
+            if (remaining_distance <= segment_lengths[i]) {
+                double ratio = remaining_distance / segment_lengths[i];
+                double new_x = points[i].x + ratio * (points[i + 1].x - points[i].x);
+                double new_y = points[i].y + ratio * (points[i + 1].y - points[i].y);
+                current_point = {new_x, new_y};
+                cout << current_point.x << ", " << current_point.y << endl;
+                break;
+            } else {
+                remaining_distance -= segment_lengths[i];
+            }
+        }
+    }
+
+    return 0;
+}
+ 
+```

problems/kamacoder/0161.讨厌鬼的组合帖子.md

@@ -0,0 +1,61 @@
+
+# 讨厌鬼的组合帖子 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1239)
+
+这个问题本质上是要找到两个数组的子集，使得这两个子集之间的差的绝对值最大。
+
+问题可以简化为寻找两个数列之间最大可能的差的绝对值。
+
+贪心思路如下：
+
+计算差异，首先，我们可以计算每个帖子的点赞数和点踩数的差值 d[i] = a[i] - b[i]。这样问题就转化为选择这些差值的一个子集，使得子集中所有元素的和的绝对值最大。
+
+遍历可能性，要使得一个数的绝对值尽可能大，可以尝试最大化这个数，或者最小化这个数（使其尽可能小于零）。我们可以分别尝试将所有正的差值加在一起，以及将所有负的差值加在一起。
+
+计算最大吸引度：
+
+* 将所有正的差值求和得到一个总和。
+* 将所有负的差值求和得到另一个总和。
+* 最后，吸引度即为这两个总和的绝对值中的较大者。
+
+
+```CPP
+
+#include <iostream>
+#include <vector>
+#include <cmath>
+
+using namespace std;
+
+int main() {
+    int n;
+    cin >> n;
+
+    vector<int> a(n), b(n);
+    for (int i = 0; i < n; ++i) {
+        cin >> a[i];
+    }
+    for (int i = 0; i < n; ++i) {
+        cin >> b[i];
+    }
+
+    long long positive_sum = 0;
+    long long negative_sum = 0;
+
+    for (int i = 0; i < n; ++i) {
+        int difference = a[i] - b[i];
+        if (difference > 0) {
+            positive_sum += difference;
+        } else if (difference < 0) {
+            negative_sum += difference;
+        }
+    }
+
+    // 最大吸引度是正总和或负总和的绝对值中的较大者
+    cout << max(abs(positive_sum), abs(negative_sum)) << endl;
+
+    return 0;
+}
+```
+

problems/kamacoder/0162.小红的第16版方案.md

@@ -0,0 +1,154 @@
+
+# 小红的第16版方案 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1240)
+
+暴力解法： （数据量已经出最大了，C++能过，java、python、go都过不了）
+
+```CPP 
+#include <bits/stdc++.h>
+using namespace std;
+int main() {
+    int n, m;
+    int l, r;
+    cin >> n >> m;
+    vector<int> a(n + 1);
+    vector<int> angry(n + 1);
+    for (int i = 1; i <= n; i++) cin >> a[i];
+    for (int i = 1; i <= m; i++) {
+        cin >> l >> r;
+        for (int j = l; j <= r; j++) {
+            angry[j]++;
+            if (angry[j] > a[j]) {
+                cout << i - 1 << endl;
+                return 0;
+            }
+        }
+    }
+    cout << m << endl;
+    return 0;
+}
+```
+
+使用 差分数组，代码如下： 
+
+
+```CPP 
+#include <iostream>
+#include <vector>
+using namespace std;
+
+int main() {
+    int n, m;
+    cin >> n >> m;
+
+    vector<int> a(n + 1);
+    for (int i = 1; i <= n; ++i) {
+        cin >> a[i];
+    }
+
+    vector<int> diff(n + 1, 0); // 差分数组，多一个元素用于处理边界情况
+
+    int l, r;
+    for (int i = 1; i <= m; ++i) {
+        cin >> l >> r;
+        diff[l]++;
+        if (r + 1 <= n) diff[r + 1]--;
+    }
+
+    int current_anger = 0;   // 当前的愤怒值
+    for (int i = 1; i <= n; ++i) {
+        current_anger += diff[i];  // 计算差分数组的前缀和，得到最终的愤怒值
+        if (current_anger > a[i]) {
+            cout << i - 1 << endl;  // 如果当前的愤怒值超过阈值，输出最后一个没有问题的方案编号
+            return 0;
+        }
+    }
+
+    cout << m << endl;  // 如果所有修改完成后都没有超过阈值，返回最后一个方案的编号
+    return 0;
+} 
+```
+
+过不了，因为差分数组只能知道是哪个人超过了阈值，不能知道是第几次修改超过的
+
+最后 优化思路：
+
+* 差分数组（Difference Array）：依然使用差分数组来处理区间更新。
+* 二分查找：通过二分查找来确定最早发生愤怒值超出阈值的操作，而不是逐次模拟每一次修改。
+
+步骤： 
+
+* 创建一个差分数组 diff 用于处理区间增加操作。
+* 在 [1, m] 的范围内进行二分查找，确定导致某个人愤怒值超过阈值的最早的修改次数。
+* 对每个二分查找的中间值 mid，我们累积应用前 mid 次操作，然后检查是否有任何人的愤怒值超过了阈值。
+* 如果 mid 之前没有超标，则继续向右查找；否则向左缩小范围。
+* 在二分查找完成后，输出找到的第一个导致愤怒值超标的操作次数。
+
+```CPP 
+#include <iostream>
+#include <vector>
+#include <algorithm>
+
+using namespace std;
+
+bool isValid(const vector<int>& a, const vector<int>& diff, int n, int m) {
+    vector<int> anger(n + 1, 0);
+    int current_anger = 0;
+    for (int i = 1; i <= n; ++i) {
+        current_anger += diff[i];
+        if (current_anger > a[i]) {
+            return false;  // 超出愤怒阈值
+        }
+    }
+    return true;  // 没有任何人超出愤怒阈值
+}
+
+int main() {
+    int n, m;
+    cin >> n >> m;
+
+    vector<int> a(n + 1);  // 愤怒阈值数组
+    for (int i = 1; i <= n; ++i) {
+        cin >> a[i];
+    }
+
+    vector<pair<int, int>> operations(m + 1);  // 保存每次操作的区间
+    for (int i = 1; i <= m; ++i) {
+        int l, r;
+        cin >> l >> r;
+        operations[i] = {l, r};
+    }
+
+    int left = 1, right = m, result = m;
+
+    while (left <= right) {
+        int mid = left + (right - left) / 2;
+
+        // 构建差分数组，只考虑前 mid 次操作
+        vector<int> diff(n + 2, 0);
+        for (int i = 1; i <= mid; ++i) {
+            int l = operations[i].first;
+            int r = operations[i].second;
+            diff[l]++;
+            if (r + 1 <= n) {
+                diff[r + 1]--;
+            }
+        }
+
+        if (isValid(a, diff, n, mid)) {
+            left = mid + 1;  // 如果在mid次操作后没有超标，继续向右搜索
+        } else {
+            result = mid - 1;  // 如果在mid次操作后超标，向左搜索
+            right = mid - 1;
+        }
+    }
+
+    cout << result << endl;
+    return 0;
+}
+
+```
+
+* 时间复杂度：O(n + m * log m)，其中 n 是成员数量，m 是操作次数。二分查找的时间复杂度为 O(log m)，每次二分查找中通过差分数组检查愤怒值的复杂度为 O(n)。
+* 空间复杂度：O(n + m)，主要用于存储差分数组和操作数组。

problems/kamacoder/第一题.md

@@ -0,0 +1,85 @@
+
+
+## 解题思路
+
+1、初始分析
+
+- 给定一个排列 `p`，我们首先构建一个 `pos` 数组，使得 `pos[i]` 表示 `i` 在排列 `p` 中的位置。
+- 我们需要判断数组 `a` 是否是一个优秀数组，即 `pos[a[i]] < pos[a[i+1]] <= pos[a[i]] + d` 对于所有 `i` 都成立。
+- 我们的目标是通过最少的相邻元素交换，使得数组 `a` 不再是一个优秀数组。
+
+2、思路
+
+- 要使数组 `a` 不再是优秀数组，我们只需要打破条件 `pos[a[i]] < pos[a[i+1]] <= pos[a[i]] + d` 中的某一个。
+- 一种简单的做法是让 `pos[a[i]]` 和 `pos[a[i+1]]` 之间的距离超过 `d`，或者直接让 `pos[a[i]] >= pos[a[i+1]]`。
+
+3、具体方法
+
+- 只需要考虑 `a` 中相邻元素的顺序，并判断如何交换 `p` 中相邻元素使得其顺序被打破。
+- 假设我们需要在 `p` 中交换某些元素来实现上述目标，那么最小的交换次数是将 `a[i]` 和 `a[i+1]` 的位置交换。
+- 如果 `pos[a[i]] + 1 == pos[a[i+1]]`，则需要一步交换。
+
+4、特别情况
+
+- 还需要考虑，如果通过交换相邻元素无法解决问题的情况。比如 `pos[a[i+1]]` 的位置无法移到 `pos[a[i]]` 的前面或超过 `d`。
+
+C++代码如下：
+
+
+```cpp
+#include <iostream>
+#include <vector>
+#include <algorithm>
+#include <climits>
+
+using namespace std;
+
+int main() {
+    int n, m, d;
+    cin >> n >> m >> d;
+
+    vector<int> p(n + 1);
+    vector<int> pos(n + 1);
+
+    // 读取排列 p，并构建位置数组 pos
+    for (int i = 1; i <= n; i++) {
+        cin >> p[i];
+        pos[p[i]] = i;
+    }
+
+    vector<int> a(m);
+    for (int i = 0; i < m; i++) {
+        cin >> a[i];
+    }
+
+    int min_operations = INT_MAX;
+
+    // 遍历数组 a 的相邻元素
+    for (int i = 0; i < m - 1; i++) {
+        int current_pos = pos[a[i]];
+        int next_pos = pos[a[i + 1]];
+
+        // 检查 pos[a[i]] < pos[a[i+1]] <= pos[a[i]] + d 是否成立
+        if (current_pos < next_pos && next_pos <= current_pos + d) {
+            // 计算需要的最少操作次数
+            int distance = next_pos - current_pos;
+
+            // Case 1: 交换 current_pos 和 next_pos
+            min_operations = min(min_operations, distance);
+
+            // Case 2: 如果 next_pos + d <= n，考虑使 pos[a[i+1]] 超过 pos[a[i]] + d
+            if (current_pos + d + 1 <= n) {
+                min_operations = min(min_operations, d + 1 - distance);
+            }
+        } else {
+            min_operations = 0;
+        }
+    }
+
+    cout << min_operations << endl;
+    return 0;
+}
+
+```
+
+时间复杂度为 O(m)

problems/kamacoder/第三题.md

@@ -0,0 +1,76 @@
+
+
+贪心思路
+
+为了保证字典序最大，我们优先放置字母 `b`，然后再放置字母 `a`。在放置字符时，我们还需注意不能超过连续 `k` 次相同字符：
+
+- 如果当前已经连续放置了 `k` 次相同字符，必须切换到另一个字符。
+- 每次放置字符后，相应的字符数量减少，同时更新当前字符的连续计数。
+
+实现步骤：
+
+- **初始化**：根据输入的 `x`, `y`, `k` 值，检查是否有可能构造出满足条件的字符串。初始化结果字符串的大小，并设置初始计数器。
+- **循环放置字符**：
+  - 优先放置字符 `b`，如果 `b` 的数量已经足够，或者已经放置了 `k` 次字符 `b`，则放置字符 `a`。
+  - 如果已经放置了 `k` 次相同字符，则强制切换到另一个字符。
+
+C++代码如下： 
+
+```CPP 
+#include<iostream>
+#include<string>
+using namespace std;
+
+int main() {
+    int countA, countB, maxRepeat;
+    cin >> countA >> countB >> maxRepeat;
+
+    // 检查是否有可能生成满足条件的字符串
+    if (countA > (countB + 1) * maxRepeat || countB > (countA + 1) * maxRepeat) {
+        cout << -1 << endl;
+        return 0;
+    }
+
+    string result(countA + countB, ' ');  // 预先分配字符串大小
+    int currentA = 0, currentB = 0;       // 当前连续 'a' 和 'b' 的计数
+    int pos = 0;                          // 当前填充位置
+
+    while (countA > 0 || countB > 0) {
+        // 当可以继续添加 'a' 或 'b' 且没有超过最大连续限制时
+        if (currentA < maxRepeat && currentB < maxRepeat) {
+            if (countA <= countB * maxRepeat) {
+                result[pos++] = 'b';
+                countB--;
+                currentB++;
+                currentA = 0;
+            } else {
+                result[pos++] = 'a';
+                countA--;
+                currentA++;
+                currentB = 0;
+            }
+        }
+
+        // 当当前字符达到最大连续限制时，切换到另一个字符
+        if (currentA == maxRepeat || currentB == maxRepeat) {
+            if (result[pos - 1] == 'a') {
+                result[pos++] = 'b';
+                countB--;
+                currentB = 1;
+                currentA = 0;
+            } else {
+                result[pos++] = 'a';
+                countA--;
+                currentA = 1;
+                currentB = 0;
+            }
+        }
+    }
+
+    cout << result << endl;
+    return 0;
+}
+
+```
+
+时间复杂度：O(n) 

problems/kamacoder/第二题.md

@@ -0,0 +1,78 @@
+
+## 解题思路 
+
+贪心思路
+
+- **计算相邻元素差值**：
+  - 对于数组 `a`，计算每对相邻元素的差值 `diff[i] = a[i+1] - a[i]`。
+  - 如果 `diff[i]` 为负数，意味着 `a[i+1]` 比 `a[i]` 小或相等，需要通过操作使 `a[i+1]` 变大。
+
+- **确定最小操作次数**：
+  - 计算所有相邻元素中的最小差值 `minDifference`，即 `minDifference = min(diff[i])`。
+  - 如果 `minDifference` 为负数或零，则需要进行 `-minDifference + 1` 次操作，使得 `a[i+1]` 大于 `a[i]`，从而使数组严格递增。
+
+- **实现细节**：
+  - 遍历数组的每对相邻元素，找出最小的差值。
+  - 根据最小差值，计算出最少的操作次数。
+
+
+
+```CPP 
+#include <iostream>
+#include <vector>
+#include <climits>
+
+using namespace std;
+
+int main()
+{
+    int n;
+    cin >> n;
+
+    vector<int> arr(n);  // 用于存储输入数组
+    vector<int> differences;  // 用于存储相邻元素的差值
+
+    for(int i = 0; i < n; i++) {
+        cin >> arr[i];
+        if(i > 0) differences.push_back(arr[i] - arr[i - 1]);
+
+    }
+
+    int minDifference = INT_MAX;
+
+    // 寻找最小的差值
+    for(int diff : differences) {
+        if(diff < minDifference) {
+            minDifference = diff;
+        }
+    }
+
+    // 如果最小差值是负数或零，计算所需的操作次数
+    int minOperations = max(0, -minDifference + 1);
+
+    cout << minOperations << endl;
+
+    return 0;
+}
+ 
+```
+关于 `-minDifference + 1` 为什么要 + 1 解释： 
+
+对于数组 `a` 中相邻的两个元素 `a[i]` 和 `a[i+1]`，我们计算它们的差值 `diff = a[i+1] - a[i]`。
+
+- **目标**：要使 `a[i] < a[i+1]`，需要 `diff > 0`。
+- 如果 `diff < 0`，说明 `a[i+1]` 比 `a[i]` 小，这时候 `a` 不是严格递增的。
+- 如果 `diff = 0`，说明 `a[i+1]` 和 `a[i]` 相等，这时也不满足严格递增。
+
+解释 `-minDifference + 1`
+
+1. **当 `minDifference < 0` 时**：
+   - 假设 `minDifference` 是所有相邻差值中的最小值，并且它是一个负数。
+   - 例如，`minDifference = -3`，表示 `a[i+1] - a[i] = -3`，也就是 `a[i+1]` 比 `a[i]` 小 `3`。
+   - 要让 `a[i+1] > a[i]`，我们至少需要使 `a[i+1] - a[i]` 从 `-3` 增加到 `1`。因此需要增加 `4`，即 `(-(-3)) + 1 = 3 + 1 = 4` 次操作。
+
+2. **当 `minDifference = 0` 时**：
+   - `minDifference` 等于 `0`，表示 `a[i+1] - a[i] = 0`，即 `a[i+1]` 和 `a[i]` 相等。
+   - 为了使 `a[i+1] > a[i]`，我们至少需要进行一次操作，使得 `a[i+1]` 大于 `a[i]`。
+
+