delete $

problems/前序/递归算法的时间与空间复杂度分析.md

@@ -26,7 +26,7 @@ int fibonacci(int i) {
 
 在讲解递归时间复杂度的时候，我们提到了递归算法的时间复杂度本质上是要看: **递归的次数 * 每次递归的时间复杂度**。
 
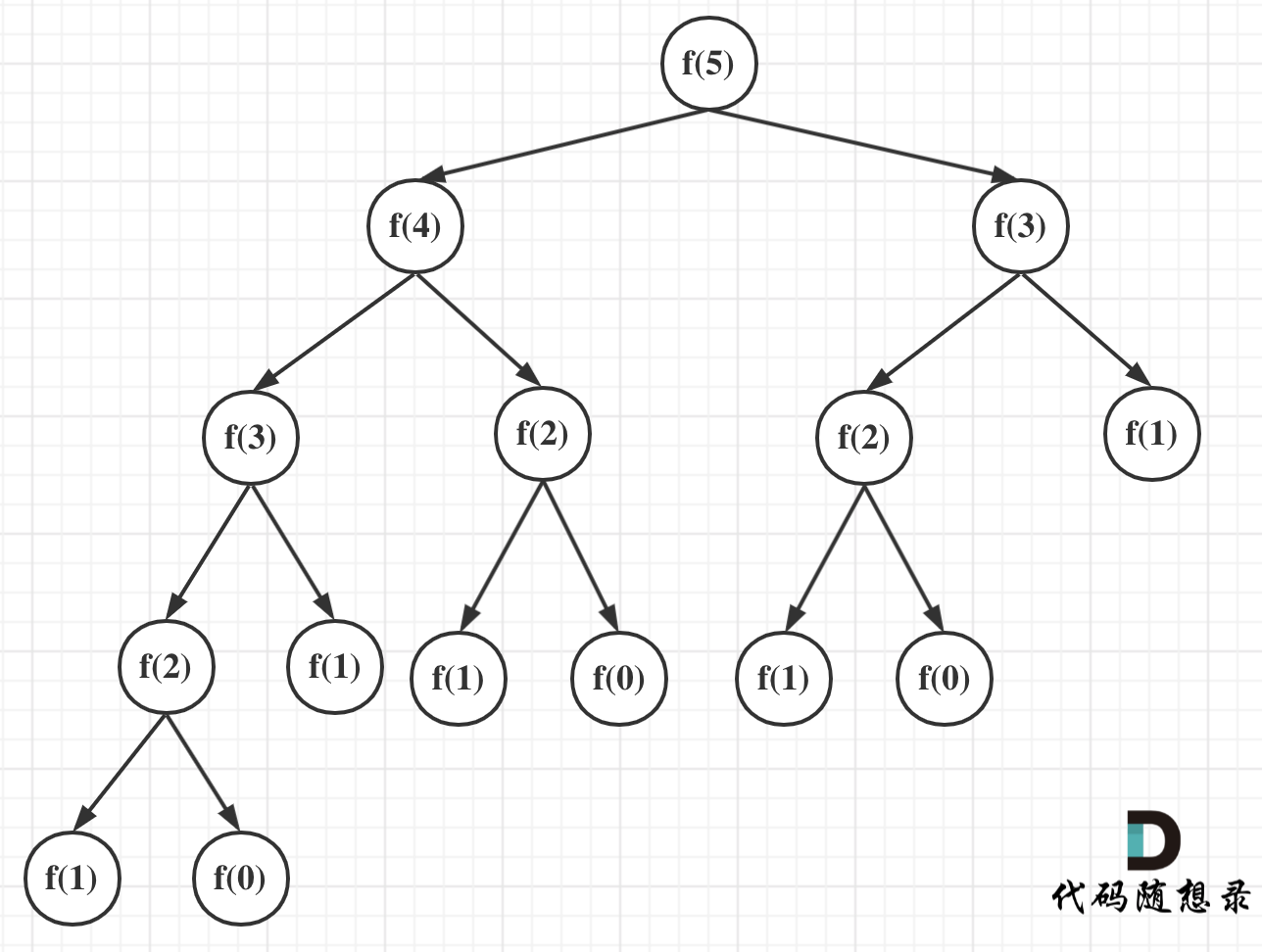
-可以看出上面的代码每次递归都是$O(1)$的操作。再来看递归了多少次，这里将i为5作为输入的递归过程 抽象成一棵递归树，如图：
+可以看出上面的代码每次递归都是O(1)的操作。再来看递归了多少次，这里将i为5作为输入的递归过程 抽象成一棵递归树，如图：
 
 ![递归空间复杂度分析](https://img-blog.csdnimg.cn/20210305093200104.png)
 
@@ -36,7 +36,7 @@ int fibonacci(int i) {
 
 我们之前也有说到，一棵深度（按根节点深度为1）为k的二叉树最多可以有 2^k - 1 个节点。
 
-所以该递归算法的时间复杂度为$O(2^n)$，这个复杂度是非常大的，随着n的增大，耗时是指数上升的。
+所以该递归算法的时间复杂度为O(2^n)，这个复杂度是非常大的，随着n的增大，耗时是指数上升的。
 
 来做一个实验，大家可以有一个直观的感受。
 
@@ -85,7 +85,7 @@ int main()
 * n = 40，耗时：837 ms
 * n = 50，耗时：110306 ms
 
-可以看出，$O(2^n)$这种指数级别的复杂度是非常大的。
+可以看出，O(2^n)这种指数级别的复杂度是非常大的。
 
 所以这种求斐波那契数的算法看似简洁，其实时间复杂度非常高，一般不推荐这样来实现斐波那契。
 
@@ -119,14 +119,14 @@ int fibonacci(int first, int second, int n) {
 
 这里相当于用first和second来记录当前相加的两个数值，此时就不用两次递归了。
 
-因为每次递归的时候n减1，即只是递归了n次，所以时间复杂度是 $O(n)$。
+因为每次递归的时候n减1，即只是递归了n次，所以时间复杂度是 O(n)。
 
-同理递归的深度依然是n，每次递归所需的空间也是常数，所以空间复杂度依然是$O(n)$。
+同理递归的深度依然是n，每次递归所需的空间也是常数，所以空间复杂度依然是O(n)。
 
 代码（版本二）的复杂度如下：
 
-* 时间复杂度：$O(n)$
-* 空间复杂度：$O(n)$
+* 时间复杂度：O(n)
+* 空间复杂度：O(n)
 
 此时再来测一下耗时情况验证一下：
 
@@ -198,7 +198,7 @@ int main()
 
 递归第n个斐波那契数的话，递归调用栈的深度就是n。
 
-那么每次递归的空间复杂度是$O(1)$， 调用栈深度为n，所以这段递归代码的空间复杂度就是$O(n)$。
+那么每次递归的空间复杂度是O(1)， 调用栈深度为n，所以这段递归代码的空间复杂度就是O(n)。
 
 ```CPP
 int fibonacci(int i) {
@@ -233,24 +233,24 @@ int binary_search( int arr[], int l, int r, int x) {
 }
 ```
 
-都知道二分查找的时间复杂度是$O(\log n)$，那么递归二分查找的空间复杂度是多少呢？
+都知道二分查找的时间复杂度是O(logn)，那么递归二分查找的空间复杂度是多少呢？
 
 我们依然看 **每次递归的空间复杂度和递归的深度**
 
 每次递归的空间复杂度可以看出主要就是参数里传入的这个arr数组，但需要注意的是在C/C++中函数传递数组参数，不是整个数组拷贝一份传入函数而是传入的数组首元素地址。
 
-**也就是说每一层递归都是公用一块数组地址空间的**，所以 每次递归的空间复杂度是常数即：$O(1)$。
+**也就是说每一层递归都是公用一块数组地址空间的**，所以 每次递归的空间复杂度是常数即：O(1)。
 
-再来看递归的深度，二分查找的递归深度是logn ，递归深度就是调用栈的长度，那么这段代码的空间复杂度为 $1 * logn = O(logn)$。
+再来看递归的深度，二分查找的递归深度是logn ，递归深度就是调用栈的长度，那么这段代码的空间复杂度为 1 * logn = O(logn)。
 
-大家要注意自己所用的语言在传递函数参数的时，是拷贝整个数值还是拷贝地址，如果是拷贝整个数值那么该二分法的空间复杂度就是$O(n\log n)$。
+大家要注意自己所用的语言在传递函数参数的时，是拷贝整个数值还是拷贝地址，如果是拷贝整个数值那么该二分法的空间复杂度就是O(nlogn)。
 
 
 ## 总结
 
 本章我们详细分析了递归实现的求斐波那契和二分法的空间复杂度，同时也对时间复杂度做了分析。
 
-特别是两种递归实现的求斐波那契数列，其时间复杂度截然不容，我们还做了实验，验证了时间复杂度为$O(2^n)$是非常耗时的。
+特别是两种递归实现的求斐波那契数列，其时间复杂度截然不容，我们还做了实验，验证了时间复杂度为O(2^n)是非常耗时的。
 
 通过本篇大家应该对递归算法的时间复杂度和空间复杂度有更加深刻的理解了。