更新动态规划专题Markdown文件

problems/背包问题理论基础完全背包.md

@@ -0,0 +1,175 @@
+# 动态规划：关于完全背包，你该了解这些！
+
+## 完全背包
+
+有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。**每件物品都有无限个（也就是可以放入背包多次）**，求解将哪些物品装入背包里物品价值总和最大。
+
+**完全背包和01背包问题唯一不同的地方就是，每种物品有无限件**。
+
+同样leetcode上没有纯完全背包问题，都是需要完全背包的各种应用，需要转化成完全背包问题，所以我这里还是以纯完全背包问题进行讲解理论和原理。
+
+在下面的讲解中，我依然举这个例子：
+
+背包最大重量为4。
+
+物品为：
+
+|       | 重量 | 价值 |
+| ---   | ---  | ---  |
+| 物品0 | 1    | 15   |
+| 物品1 | 3    | 20   |
+| 物品2 | 4    | 30   |
+
+**每件商品都有无限个！**
+
+问背包能背的物品最大价值是多少？
+
+01背包和完全背包唯一不同就是体现在遍历顺序上，所以本文就不去做动规五部曲了，我们直接针对遍历顺序经行分析！
+
+关于01背包我如下两篇已经进行深入分析了：
+
+* [动态规划：关于01背包问题，你该了解这些！](https://mp.weixin.qq.com/s/FwIiPPmR18_AJO5eiidT6w)
+* [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://mp.weixin.qq.com/s/M4uHxNVKRKm5HPjkNZBnFA)
+
+首先在回顾一下01背包的核心代码
+```
+for(int i = 0; i < weight.size(); i++) { // 遍历物品
+    for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
+        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+    }
+}
+```
+
+我们知道01背包内嵌的循环是从大到小遍历，为了保证每个物品仅被添加一次。
+
+而完全背包的物品是可以添加多次的，所以要从小到大去遍历，即：
+
+```C++
+// 先遍历物品，再遍历背包
+for(int i = 0; i < weight.size(); i++) { // 遍历物品
+    for(int j = weight[i]; j < bagWeight ; j++) { // 遍历背包容量
+        dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+
+    }
+}
+```
+
+至于为什么，我在[动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://mp.weixin.qq.com/s/M4uHxNVKRKm5HPjkNZBnFA)中也做了讲解。
+
+dp状态图如下：
+
+![动态规划-完全背包](https://img-blog.csdnimg.cn/20210126104510106.jpg)
+
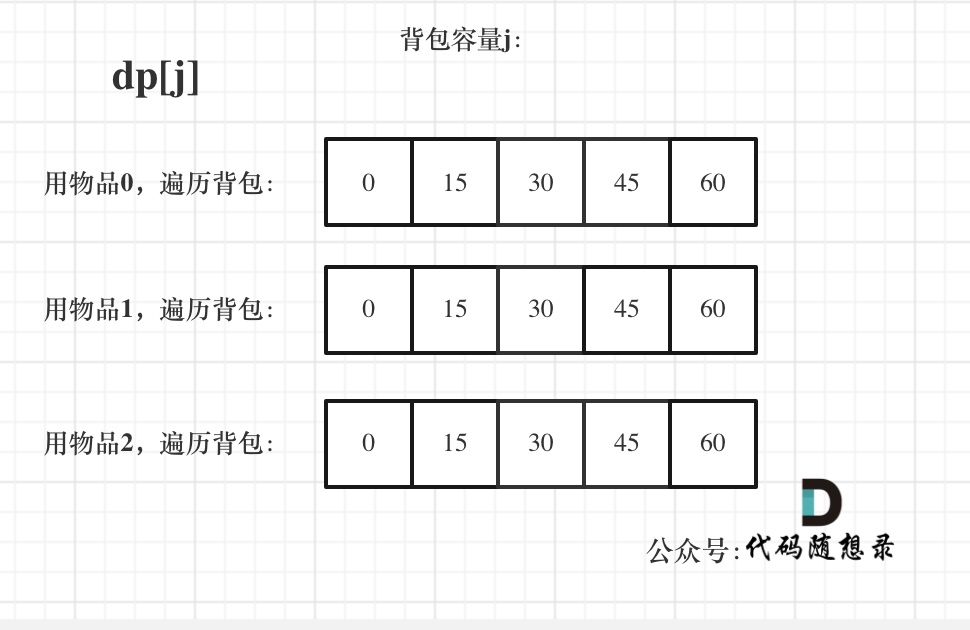
+相信很多同学看网上的文章，关于完全背包介绍基本就到为止了。
+
+**其实还有一个很重要的问题，为什么遍历物品在外层循环，遍历背包容量在内层循环？**
+
+这个问题很多题解关于这里都是轻描淡写就略过了，大家都默认 遍历物品在外层，遍历背包容量在内层，好像本应该如此一样，那么为什么呢？
+
+难道就不能遍历背包容量在外层，遍历物品在内层？
+
+
+看过这两篇的话：
+* [动态规划：关于01背包问题，你该了解这些！](https://mp.weixin.qq.com/s/FwIiPPmR18_AJO5eiidT6w)
+* [动态规划：关于01背包问题，你该了解这些！（滚动数组）](https://mp.weixin.qq.com/s/M4uHxNVKRKm5HPjkNZBnFA)
+
+就知道了，01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了，一位dp数组的两个for循环先后循序一定是先遍历物品，再遍历背包容量。
+
+**在完全背包中，对于一维dp数组来说，其实两个for循环嵌套顺序同样无所谓！**
+
+因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
+
+遍历物品在外层循环，遍历背包容量在内层循环，状态如图：
+
+![动态规划-完全背包1](https://img-blog.csdnimg.cn/20210126104529605.jpg)
+
+遍历背包容量在外层循环，遍历物品在内层循环，状态如图：
+
+![动态规划-完全背包2](https://img-blog.csdnimg.cn/20210126104741304.jpg)
+
+看了这两个图，大家就会理解，完全背包中，两个for循环的先后循序，都不影响计算dp[j]所需要的值（这个值就是下标j之前所对应的dp[j]）。
+
+先遍历被背包在遍历物品，代码如下：
+
+```C++
+// 先遍历背包，再遍历物品
+for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
+    for(int i = 0; i < weight.size(); i++) { // 遍历物品
+        if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+    }
+    cout << endl;
+}
+```
+
+## C++测试代码
+
+完整的C++测试代码如下：
+
+```C++
+// 先遍历物品，在遍历背包
+void test_CompletePack() {
+    vector<int> weight = {1, 3, 4};
+    vector<int> value = {15, 20, 30};
+    int bagWeight = 4;
+    vector<int> dp(bagWeight + 1, 0);
+    for(int i = 0; i < weight.size(); i++) { // 遍历物品
+        for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
+            dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+        }
+    }
+    cout << dp[bagWeight] << endl;
+}
+int main() {
+    test_CompletePack();
+}
+
+```
+
+```C++
+
+// 先遍历背包，再遍历物品
+void test_CompletePack() {
+    vector<int> weight = {1, 3, 4};
+    vector<int> value = {15, 20, 30};
+    int bagWeight = 4;
+
+    vector<int> dp(bagWeight + 1, 0);
+
+    for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
+        for(int i = 0; i < weight.size(); i++) { // 遍历物品
+            if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
+        }
+    }
+    cout << dp[bagWeight] << endl;
+}
+int main() {
+    test_CompletePack();
+}
+
+```
+
+
+## 总结
+
+细心的同学可能发现，**全文我说的都是对于纯完全背包问题，其for循环的先后循环是可以颠倒的！**
+
+但如果题目稍稍有点变化，就会体现在遍历顺序上。
+
+如果问装满背包有几种方式的话？ 那么两个for循环的先后顺序就有很大区别了，而leetcode上的题目都是这种稍有变化的类型。
+
+这个区别，我将在后面讲解具体leetcode题目中给大家介绍，因为这块如果不结合具题目，单纯的介绍原理估计很多同学会越看越懵！
+
+别急，下一篇就是了！哈哈
+
+最后，**又可以出一道面试题了，就是纯完全背包，要求先用二维dp数组实现，然后再用一维dp数组实现，最后在问，两个for循环的先后是否可以颠倒？为什么？**
+这个简单的完全背包问题，估计就可以难住不少候选人了。
+
+> **相信很多小伙伴刷题的时候面对力扣上近两千道题目，感觉无从下手，我花费半年时间整理了Github项目：「力扣刷题攻略」[https://github.com/youngyangyang04/leetcode-master](https://github.com/youngyangyang04/leetcode-master)。 里面有100多道经典算法题目刷题顺序、配有40w字的详细图解，常用算法模板总结，以及难点视频讲解，按照list一道一道刷就可以了！star支持一波吧！**
+
+* 公众号：[代码随想录](https://img-blog.csdnimg.cn/20210210152223466.png)
+* B站：[代码随想录](https://space.bilibili.com/525438321)
+* Github：[leetcode-master](https://github.com/youngyangyang04/leetcode-master)
+* 知乎：[代码随想录](https://www.zhihu.com/people/sun-xiu-yang-64)
+
+![](https://img-blog.csdnimg.cn/20210205113044152.png)
+