替换图片链接

problems/背包问题理论基础完全背包.md

@@ -66,7 +66,7 @@
 
 推导方向如图： 
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241126112952.png)
+![](https://file.kamacoder.com/pics/20241126112952.png)
 
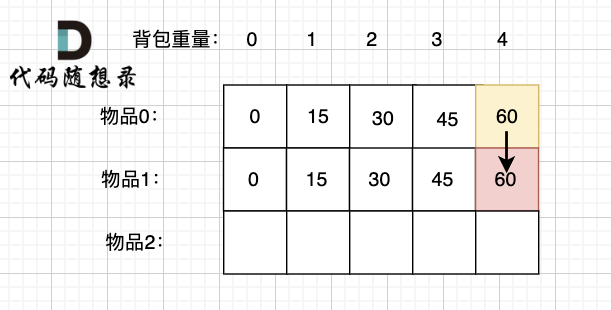
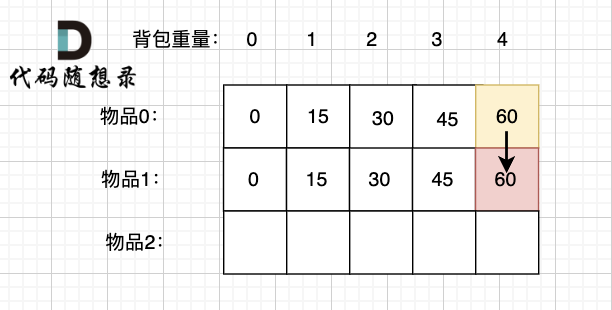
 如果放物品1， **那么背包要先留出物品1的容量**，目前容量是4，物品1 的容量（就是物品1的重量）为3，此时背包剩下容量为1。 
 
@@ -78,7 +78,7 @@
 
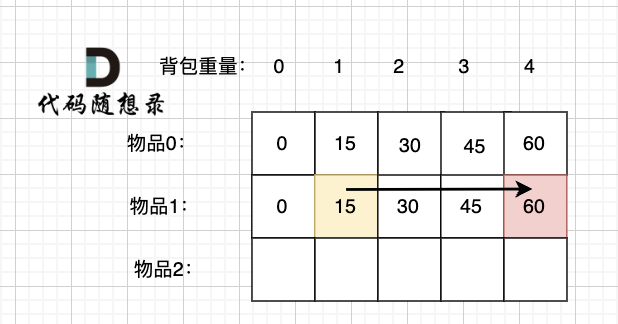
 所以 放物品1 的情况 = dp[1][1] + 物品1 的价值，推导方向如图：  
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241126113104.png)
+![](https://file.kamacoder.com/pics/20241126113104.png)
 
 
 （**注意上图和  [01背包理论基础（二维数组）](https://programmercarl.com/背包理论基础01背包-1.html) 中的区别**，对于理解完全背包很重要）
@@ -103,7 +103,7 @@
 
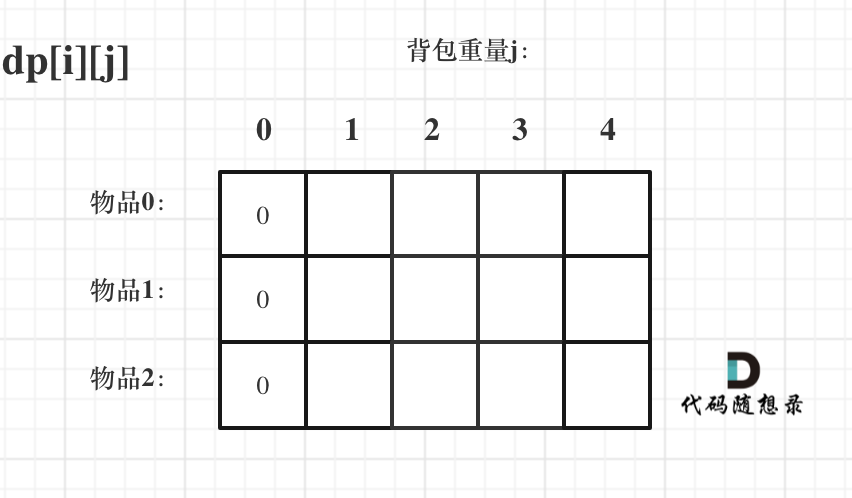
 首先从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。如图：
 
-![动态规划-背包问题2](https://code-thinking-1253855093.file.myqcloud.com/pics/2021011010304192.png)
+![动态规划-背包问题2](https://file.kamacoder.com/pics/2021011010304192.png)
 
 在看其他情况。
 
@@ -132,7 +132,7 @@ for (int j = weight[0]; j <= bagWeight; j++)
 
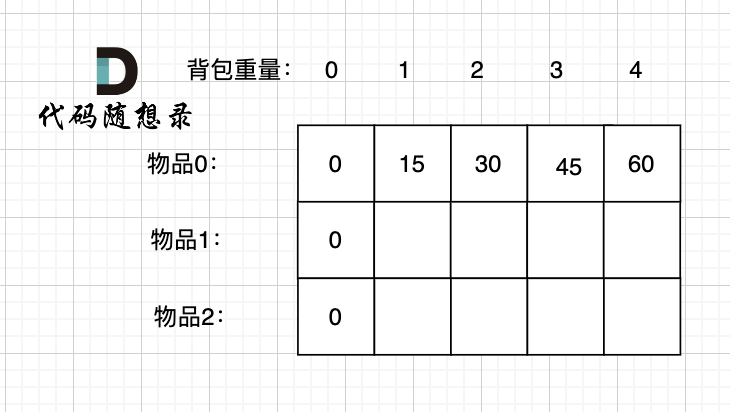
 此时dp数组初始化情况如图所示：
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241114161608.png)
+![](https://file.kamacoder.com/pics/20241114161608.png)
 
 dp[0][j] 和 dp[i][0] 都已经初始化了，那么其他下标应该初始化多少呢？
 
@@ -185,7 +185,7 @@ for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
 
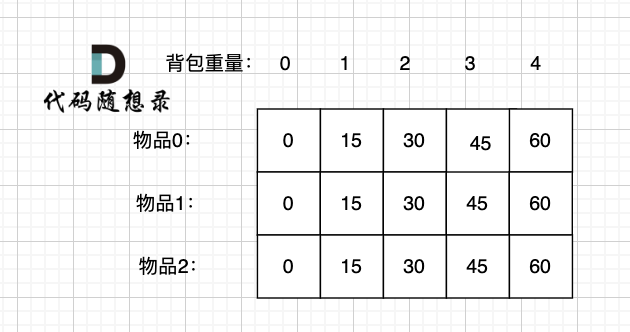
 以本篇举例数据为例，填满了dp二维数组如图： 
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20241126113752.png)
+![](https://file.kamacoder.com/pics/20241126113752.png)
 
 因为 物品0 的性价比是最高的，而且 在完全背包中，每一类物品都有无限个，所以有无限个物品0，既然物品0 性价比最高，当然是优先放物品0。