CS_learn/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2026-02-02 18:39:09 +08:00
Code Issues Packages Projects Releases Wiki Activity

替换图片链接

Browse Source
This commit is contained in:
programmercarl
2025-03-17 15:52:23 +08:00
parent 91e7dab72c
commit 86a0208485
216 changed files with 813 additions and 813 deletions
Download Patch File Download Diff File Expand all files Collapse all files

10
problems/0096.不同的二叉搜索树.md
View File

@@ -12,7 +12,7 @@
示例:
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20210113161941835.png)
![](https://file.kamacoder.com/pics/20210113161941835.png)
## 算法公开课
@@ -27,11 +27,11 @@
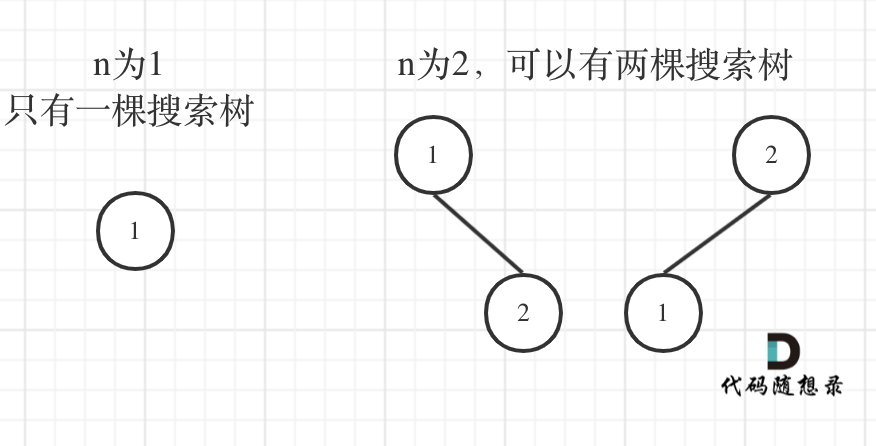
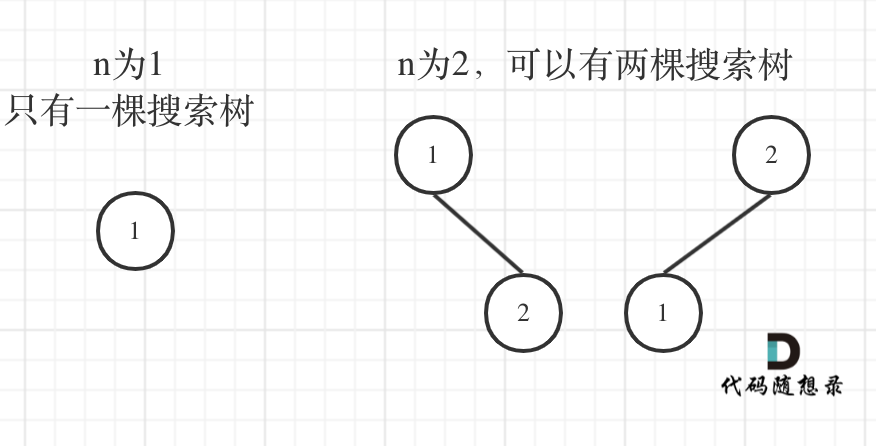
了解了二叉搜索树之后，我们应该先举几个例子，画画图，看看有没有什么规律，如图：
![96.不同的二叉搜索树](https://code-thinking-1253855093.file.myqcloud.com/pics/20210107093106367.png)
![96.不同的二叉搜索树](https://file.kamacoder.com/pics/20210107093106367.png)
n为1的时候有一棵树，n为2有两棵树，这个是很直观的。
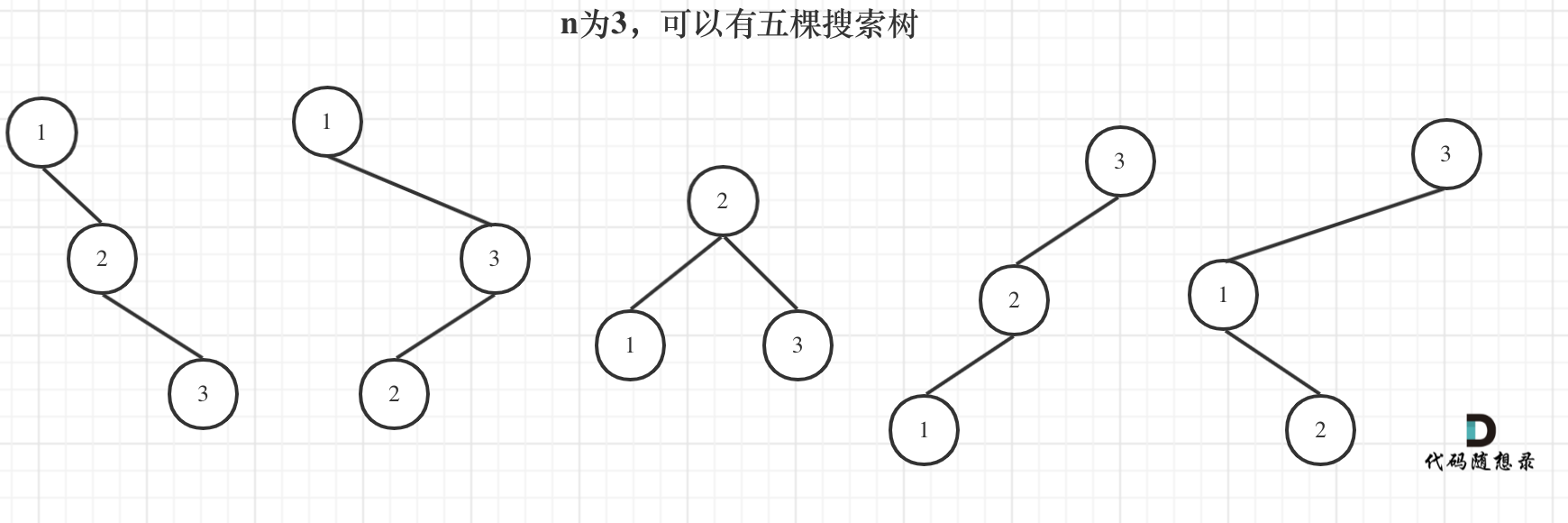
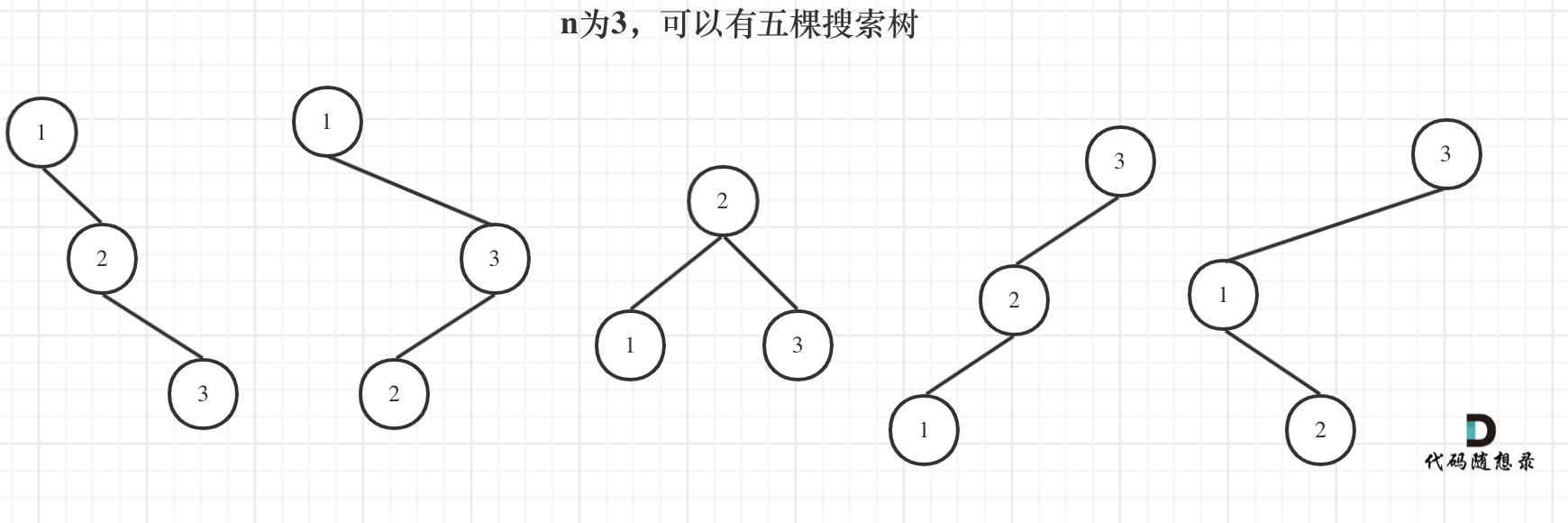
![96.不同的二叉搜索树1](https://code-thinking-1253855093.file.myqcloud.com/pics/20210107093129889.png)
![96.不同的二叉搜索树1](https://file.kamacoder.com/pics/20210107093129889.png)
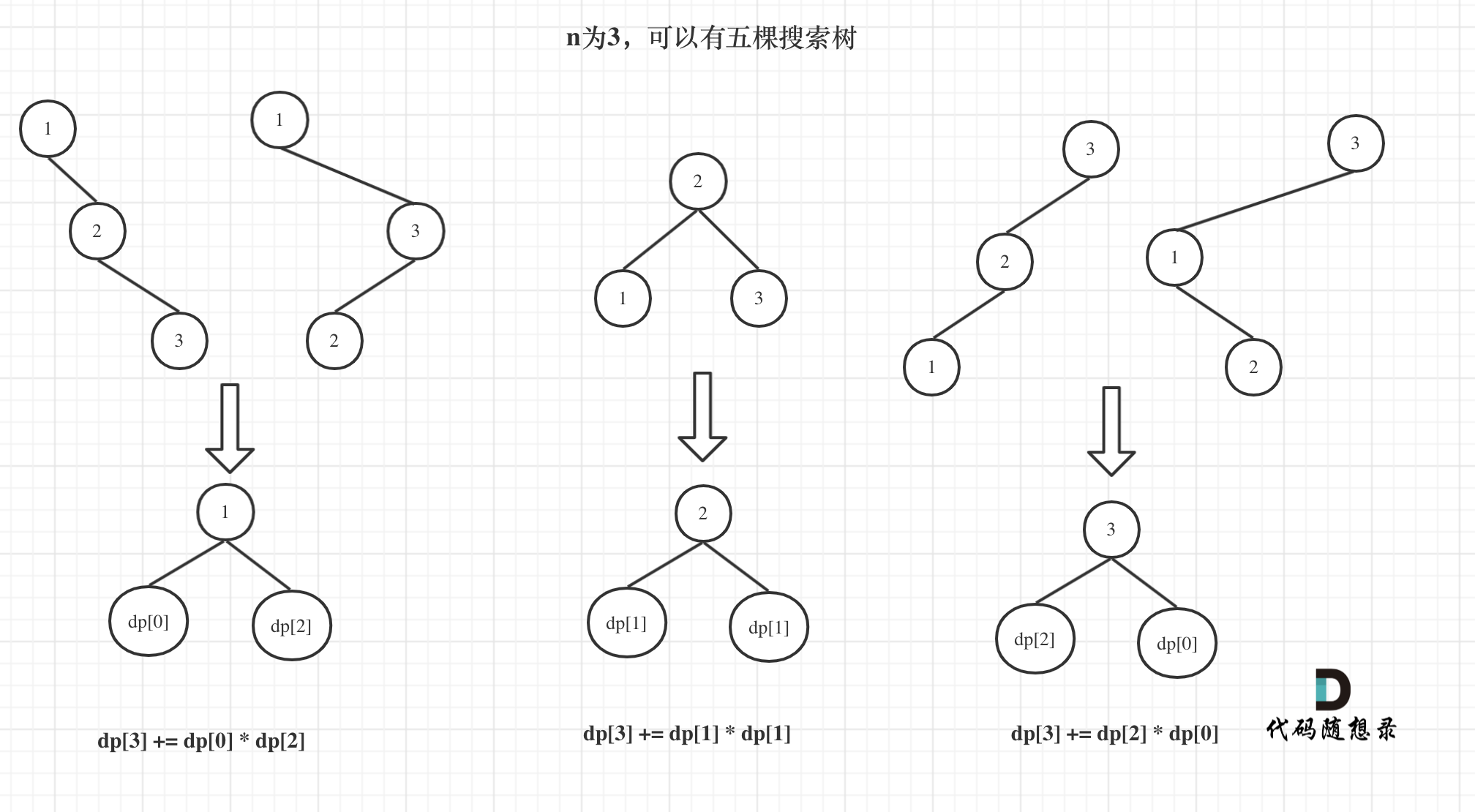
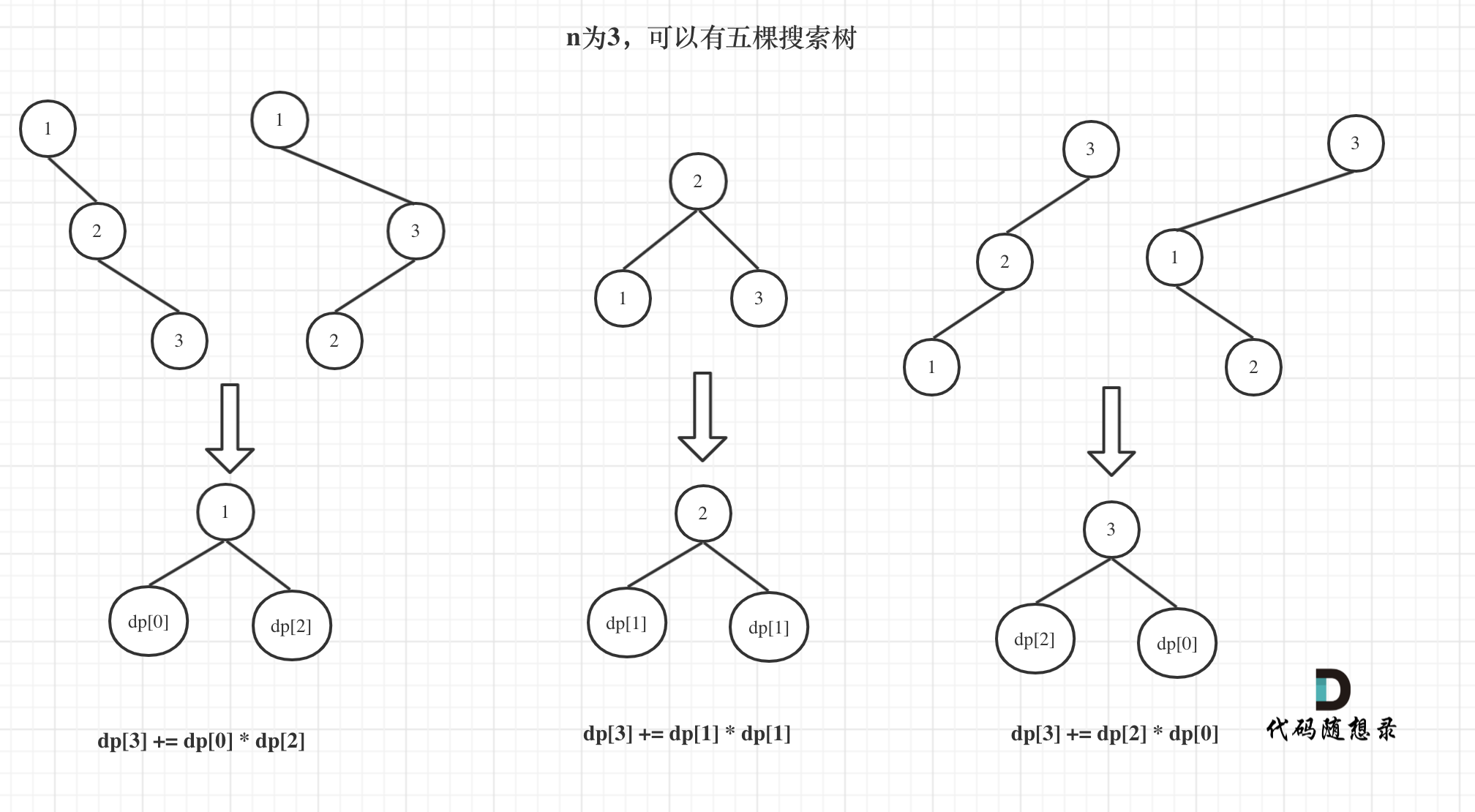
来看看n为3的时候，有哪几种情况。
@@ -65,7 +65,7 @@ dp[3]，就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索
如图所示：
![96.不同的二叉搜索树2](https://code-thinking-1253855093.file.myqcloud.com/pics/20210107093226241.png)
![96.不同的二叉搜索树2](https://file.kamacoder.com/pics/20210107093226241.png)
此时我们已经找到递推关系了，那么可以用动规五部曲再系统分析一遍。
@@ -118,7 +118,7 @@ for (int i = 1; i <= n; i++) {
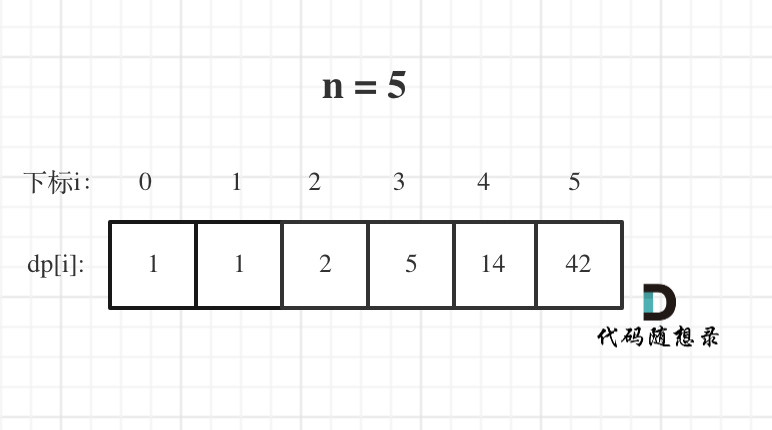
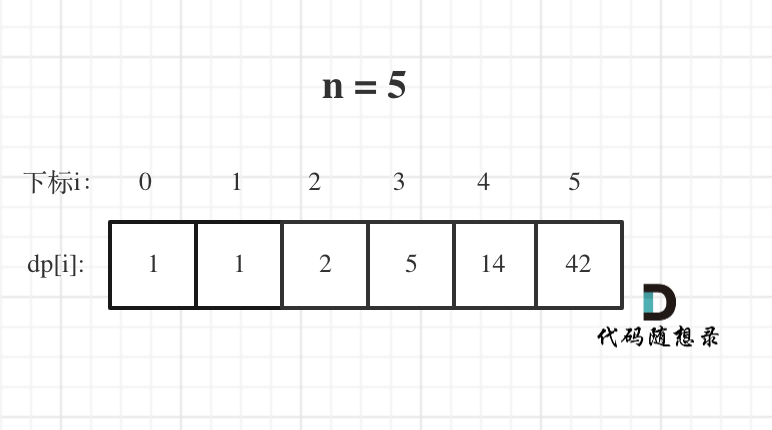
n为5时候的dp数组状态如图：
![96.不同的二叉搜索树3](https://code-thinking-1253855093.file.myqcloud.com/pics/20210107093253987.png)
![96.不同的二叉搜索树3](https://file.kamacoder.com/pics/20210107093253987.png)
当然如果自己画图举例的话，基本举例到n为3就可以了，n为4的时候，画图已经比较麻烦了。