Merge branch 'youngyangyang04:master' into master

2026-02-11 14:45:14 +08:00 · 2024-08-18 15:00:22 -07:00
parent aefb7aa83d f16c640b28
commit c366f26c30
56 changed files with 3536 additions and 930 deletions
--- a/problems/kamacoder/0044.开发商购买土地.md
+++ b/problems/kamacoder/0044.开发商购买土地.md
@@ -1,6 +1,10 @@

 # 44. 开发商购买土地 

+> 本题为代码随想录后续扩充题目，还没有视频讲解，顺便让大家练习一下ACM输入输出模式（笔试面试必备）
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1044)
+
 【题目描述】

 在一个城市区域内，被划分成了n * m个连续的区块，每个区块都拥有不同的权值，代表着其土地价值。目前，有两家开发公司，A 公司和 B 公司，希望购买这个城市区域的土地。
@@ -57,7 +61,7 @@

 如果本题要求 任何两个行（或者列）之间的数值总和，大家在[0058.区间和](./0058.区间和.md) 的基础上 应该知道怎么求。  

-就是前缀和的思路，先统计好，前n行的和 q[n]，如果要求矩阵 a 行到 b行 之间的总和，那么就 q[b] - q[a - 1]就好。 
+就是前缀和的思路，先统计好，前n行的和 q[n]，如果要求矩阵 a行 到 b行 之间的总和，那么就 q[b] - q[a - 1]就好。 

 至于为什么是 a - 1，大家去看 [0058.区间和](./0058.区间和.md) 的分析，使用 前缀和 要注意 区间左右边的开闭情况。 

--- a/problems/kamacoder/0053.寻宝-Kruskal.md
+++ b/problems/kamacoder/0053.寻宝-Kruskal.md
@@ -38,7 +38,7 @@
 5 6 2
 5 7 1
 6 7 1
-``` 
+```

 输出示例： 

@@ -79,7 +79,7 @@ kruscal的思路：

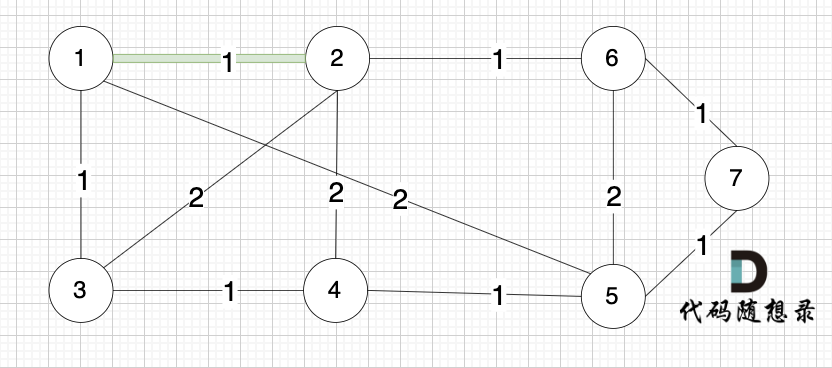
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240111114204.png)

-------- 
+--------

 选边(4,5)，节点4 和 节点 5 不在同一个集合，生成树可以添加边(4,5) ，并将节点4，节点5 放到同一个集合。 

@@ -87,7 +87,7 @@ kruscal的思路：

 **大家判断两个节点是否在同一个集合，就看图中两个节点是否有绿色的粗线连着就行**

------ 
+------

 （这里在强调一下，以下选边是按照上面排序好的边的数组来选择的）

@@ -95,13 +95,13 @@ kruscal的思路：

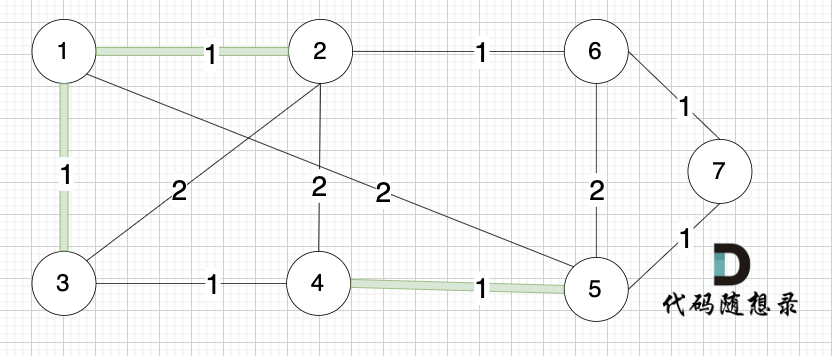
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240112105834.png) 

--------- 
+---------

 选边(2,6)，节点2 和 节点6 不在同一个集合，生成树添加边(2,6)，并将节点2，节点6 放到同一个集合。

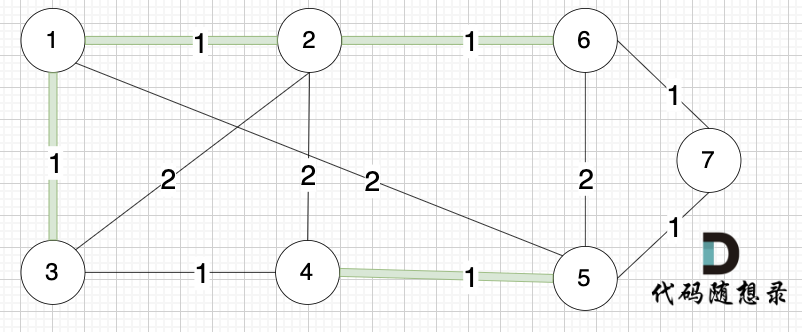
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240112110214.png) 

-------- 
+--------

 选边(3,4)，节点3 和 节点4 不在同一个集合，生成树添加边(3,4)，并将节点3，节点4 放到同一个集合。 

@@ -113,7 +113,7 @@ kruscal的思路：

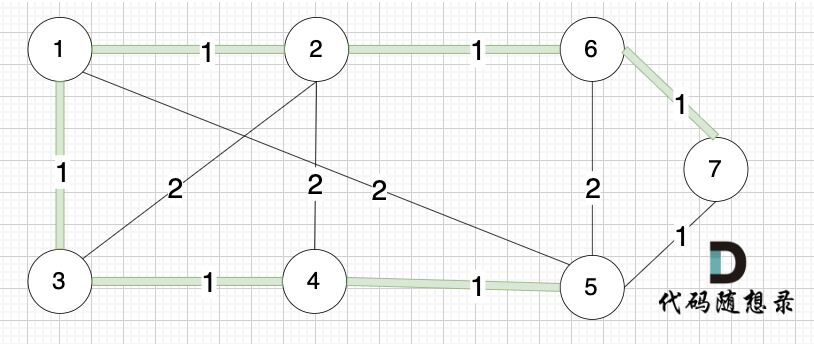
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240112110637.png) 

----------- 
+-----------

 选边(5,7)，节点5 和 节点7 在同一个集合，不做计算。 

@@ -122,7 +122,7 @@ kruscal的思路：
 后面遍历 边(3,2)，(2,4)，(5,6) 同理，都因两个节点已经在同一集合，不做计算。


------- 
+-------

 此时 我们就已经生成了一个最小生成树，即： 

@@ -230,7 +230,7 @@ int main() {

 如果题目要求将最小生成树的边输出的话，应该怎么办呢？ 

-Kruskal 算法 输出边的话，相对prim 要容易很多，因为 Kruskal 本来就是直接操作边，边的结构自然清晰，不用像 prim一样 需要再节点练成线输出边 （因为prim是对节点操作，而 Kruskal是对边操作，这是本质区别） 
+Kruskal 算法 输出边的话，相对prim 要容易很多，因为 Kruskal 本来就是直接操作边，边的结构自然清晰，不用像 prim一样 需要再将节点连成线输出边 （因为prim是对节点操作，而 Kruskal是对边操作，这是本质区别） 

 本题中，边的结构为： 

--- a/problems/kamacoder/0058.区间和.md
+++ b/problems/kamacoder/0058.区间和.md
@@ -1,6 +1,8 @@

 # 58. 区间和 

+> 本题为代码随想录后续扩充题目，还没有视频讲解，顺便让大家练习一下ACM输入输出模式（笔试面试必备）
+
 [题目链接](https://kamacoder.com/problempage.php?pid=1070)

 题目描述
@@ -97,11 +99,11 @@ int main() {

 为什么呢？ 

-p[1] = vec[0] + vec[1]; 
+`p[1] = vec[0] + vec[1];`

-p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];
+`p[5] = vec[0] + vec[1] + vec[2] + vec[3] + vec[4] + vec[5];`

-p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];
+`p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];`

 这不就是我们要求的 下标 2 到下标 5 之间的累加和吗。 

@@ -109,15 +111,17 @@ p[5] - p[1] = vec[2] + vec[3] + vec[4] + vec[5];

 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240627111319.png)

-p[5] - p[1] 就是 红色部分的区间和。 
+`p[5] - p[1]` 就是 红色部分的区间和。 

-而 p 数组是我们之前就计算好的累加和，所以后面每次求区间和的之后 我们只需要 O(1)的操作。 
+而 p 数组是我们之前就计算好的累加和，所以后面每次求区间和的之后 我们只需要 O(1) 的操作。 

 **特别注意**： 在使用前缀和求解的时候，要特别注意 求解区间。 

 如上图，如果我们要求 区间下标 [2, 5] 的区间和，那么应该是 p[5] - p[1]，而不是 p[5] - p[2]。 

-很多录友在使用前缀和的时候，分不清前缀和的区间，建议画一画图，模拟一下 思路会更清晰。
+**很多录友在使用前缀和的时候，分不清前缀和的区间，建议画一画图，模拟一下 思路会更清晰**。 
+
+本题C++代码如下：

 ```CPP
 #include <iostream>
--- a/problems/kamacoder/0094.城市间货物运输I-SPFA.md
+++ b/problems/kamacoder/0094.城市间货物运输I-SPFA.md
@@ -64,7 +64,7 @@

 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240328104119.png)  

-本图中，对所有边进行松弛，真正有效的松弛，只有松弛 边（节点1->节点2） 和 边（节点1->节点5） 。
+本图中，对所有边进行松弛，真正有效的松弛，只有松弛 边（节点1->节点2） 和 边（节点1->节点3） 。

 而松弛 边（节点4->节点6） ，边（节点5->节点3）等等 都是无效的操作，因为 节点4 和 节点 5 都是没有被计算过的节点。

@@ -158,16 +158,11 @@

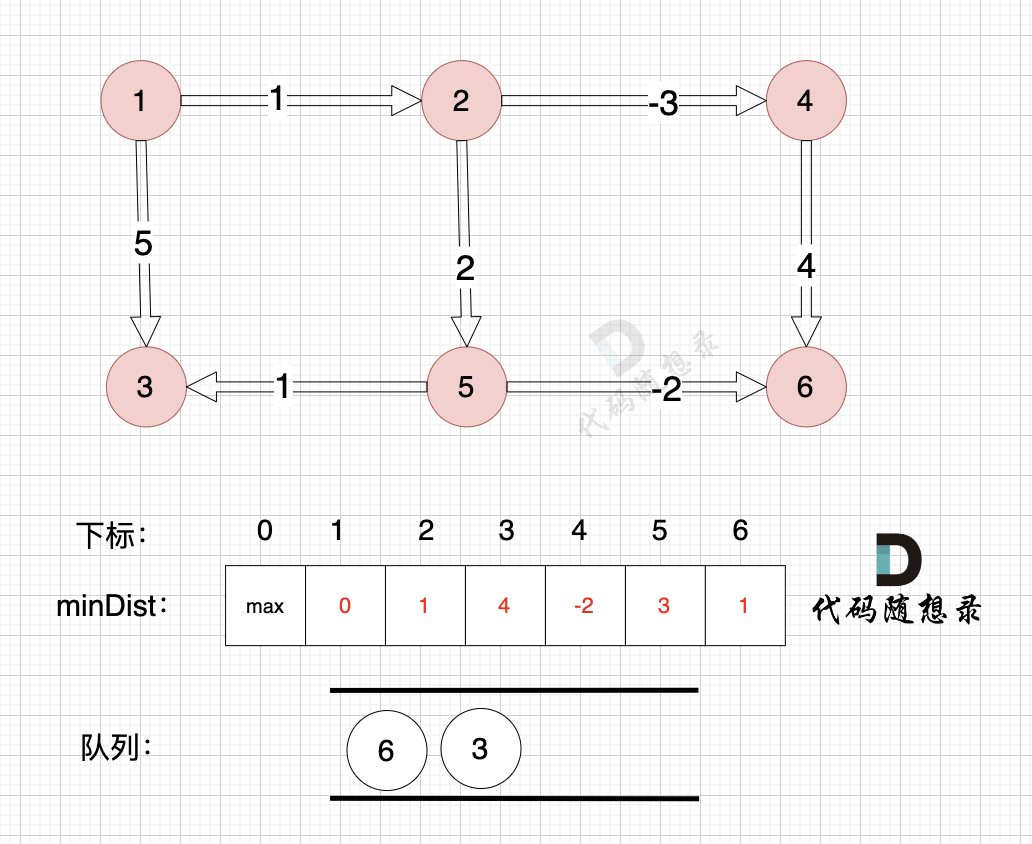
 边：节点5 -> 节点6，权值为-2 ，minDist[6] > minDist[5] + (-2) ，更新 minDist[6] = minDist[5] + (-2) = 3 - 2 = 1

-如图： 
+如图，将节点3加入队列，因为节点6已经在队列里，所以不用重复添加

-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240412110509.png)
-
-
-
-因为节点3 和 节点6 都曾经加入过队列，不用重复加入，避免重复计算。   
-
-在代码中我们可以用一个数组 visited 来记录入过队列的元素，加入过队列的元素，不再重复入队列。
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240729161116.png)

+所以我们在加入队列的过程可以有一个优化，**用visited数组记录已经在队列里的元素，已经在队列的元素不用重复加入**

 -------------- 

@@ -175,11 +170,12 @@

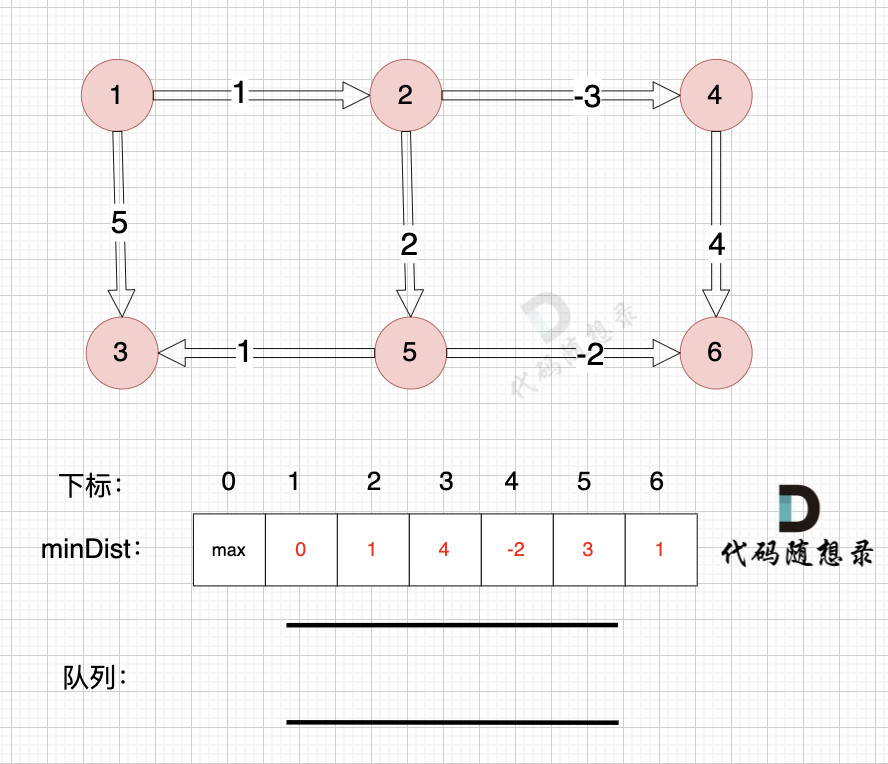
 节点6作为终点，没有可以出发的边。 

+同理从队列中取出节点3，也没有可以出发的边
+
 所以直接从队列中取出，如图： 

 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240411115424.png) 

-
 ----------

 这样我们就完成了基于队列优化的bellman_ford的算法模拟过程。 
@@ -190,12 +186,12 @@

 在上面模拟过程中，我们每次都要知道 一个节点作为出发点连接了哪些节点。 

-如果想方便知道这些数据，就需要使用邻接表来存储这个图，如果对于邻接表不了解的话，可以看 [kama0047.参会dijkstra堆](./kama0047.参会dijkstra堆.md) 中 图的存储 部分。 
+如果想方便知道这些数据，就需要使用邻接表来存储这个图，如果对于邻接表不了解的话，可以看 [kama0047.参会dijkstra堆](./0047.参会dijkstra堆.md) 中 图的存储 部分。 


 整体代码如下：

-```CPP
+```
 #include <iostream>
 #include <vector>
 #include <queue>
@@ -215,7 +211,9 @@ int main() {
    int n, m, p1, p2, val;
    cin >> n >> m;

-    vector<list<Edge>> grid(n + 1); // 邻接表
+    vector<list<Edge>> grid(n + 1); 
+
+    vector<bool> isInQueue(n + 1); // 加入优化，已经在队里里的元素不用重复添加

    // 将所有边保存起来
    for(int i = 0; i < m; i++){
@@ -230,24 +228,26 @@ int main() {
    minDist[start] = 0;

    queue<int> que;
-    que.push(start); // 队列里放入起点
+    que.push(start); 

    while (!que.empty()) {

        int node = que.front(); que.pop();
-
+        isInQueue[node] = false; // 从队列里取出的时候，要取消标记，我们只保证已经在队列里的元素不用重复加入
        for (Edge edge : grid[node]) {
            int from = node;
            int to = edge.to;
            int value = edge.val;
            if (minDist[to] > minDist[from] + value) { // 开始松弛
-                minDist[to] = minDist[from] + value;
-                que.push(to);
+                minDist[to] = minDist[from] + value; 
+                if (isInQueue[to] == false) { // 已经在队列里的元素不用重复添加
+                    que.push(to);
+                    isInQueue[to] = true;
+                }
            }
        }

    }
-
    if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
    else cout << minDist[end] << endl; // 到达终点最短路径
 }
--- a/problems/kamacoder/0098.所有可达路径.md
+++ b/problems/kamacoder/0098.所有可达路径.md
@@ -422,7 +422,8 @@ int main() {
 ## 其他语言版本

 ### Java 
-#### 邻接矩阵写法
+
+邻接矩阵写法
 ```java
 import java.util.ArrayList;
 import java.util.List;
@@ -477,7 +478,7 @@ public class Main {
 }
 ```

-#### 邻接表写法
+邻接表写法
 ```java
 import java.util.ArrayList;
 import java.util.LinkedList;
@@ -533,7 +534,7 @@ public class Main {
 }
 ```
 ### Python
-#### 邻接矩阵写法
+邻接矩阵写法
 ``` python
 def dfs(graph, x, n, path, result):
    if x == n:
@@ -566,7 +567,7 @@ if __name__ == "__main__":
    main()
 ```

-#### 邻接表写法
+邻接表写法
 ``` python
 from collections import defaultdict

@@ -604,6 +605,125 @@ if __name__ == "__main__":
 ```
 ### Go

+#### 邻接矩阵写法
+```go
+package main
+
+import (
+	"fmt"
+)
+
+var result [][]int // 收集符合条件的路径
+var path []int     // 1节点到终点的路径
+
+func dfs(graph [][]int, x, n int) {
+	// 当前遍历的节点x 到达节点n
+	if x == n { // 找到符合条件的一条路径
+		temp := make([]int, len(path))
+		copy(temp, path)
+		result = append(result, temp)
+		return
+	}
+	for i := 1; i <= n; i++ { // 遍历节点x链接的所有节点
+		if graph[x][i] == 1 { // 找到 x链接的节点
+			path = append(path, i)    // 遍历到的节点加入到路径中来
+			dfs(graph, i, n)          // 进入下一层递归
+			path = path[:len(path)-1] // 回溯，撤销本节点
+		}
+	}
+}
+
+func main() {
+	var n, m int
+	fmt.Scanf("%d %d", &n, &m)
+
+	// 节点编号从1到n，所以申请 n+1 这么大的数组
+	graph := make([][]int, n+1)
+	for i := range graph {
+		graph[i] = make([]int, n+1)
+	}
+
+	for i := 0; i < m; i++ {
+		var s, t int
+		fmt.Scanf("%d %d", &s, &t)
+		// 使用邻接矩阵表示无向图，1 表示 s 与 t 是相连的
+		graph[s][t] = 1
+	}
+
+	path = append(path, 1) // 无论什么路径已经是从1节点出发
+	dfs(graph, 1, n)       // 开始遍历
+
+	// 输出结果
+	if len(result) == 0 {
+		fmt.Println(-1)
+	} else {
+		for _, pa := range result {
+			for i := 0; i < len(pa)-1; i++ {
+				fmt.Print(pa[i], " ")
+			}
+			fmt.Println(pa[len(pa)-1])
+		}
+	}
+}
+```
+
+#### 邻接表写法
+```go
+package main
+
+import (
+	"fmt"
+)
+
+var result [][]int
+var path []int
+
+func dfs(graph [][]int, x, n int) {
+	if x == n {
+		temp := make([]int, len(path))
+		copy(temp, path)
+		result = append(result, temp)
+		return
+	}
+	for _, i := range graph[x] {
+		path = append(path, i)
+		dfs(graph, i, n)
+		path = path[:len(path)-1]
+	}
+}
+
+func main() {
+	var n, m int
+	fmt.Scanf("%d %d", &n, &m)
+
+	graph := make([][]int, n+1)
+	for i := 0; i <= n; i++ {
+		graph[i] = make([]int, 0)
+	}
+
+	for m > 0 {
+		var s, t int
+		fmt.Scanf("%d %d", &s, &t)
+		graph[s] = append(graph[s], t)
+		m--
+	}
+
+	path = append(path, 1)
+	dfs(graph, 1, n)
+
+	if len(result) == 0 {
+		fmt.Println(-1)
+	} else {
+		for _, pa := range result {
+			for i := 0; i < len(pa)-1; i++ {
+				fmt.Print(pa[i], " ")
+			}
+			fmt.Println(pa[len(pa)-1])
+		}
+	}
+}
+```
+
 ### Rust

 ### Javascript
--- a/problems/kamacoder/0100.岛屿的最大面积.md
+++ b/problems/kamacoder/0100.岛屿的最大面积.md
@@ -322,6 +322,72 @@ print(result)

 ### Go

+``` go
+
+package main
+
+import (
+	"fmt"
+)
+
+var count int
+var dir = [][]int{{0, 1}, {1, 0}, {-1, 0}, {0, -1}} // 四个方向
+
+func dfs(grid [][]int, visited [][]bool, x, y int) {
+	for i := 0; i < 4; i++ {
+		nextx := x + dir[i][0]
+		nexty := y + dir[i][1]
+		if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {
+			continue // 越界了，直接跳过
+		}
+		if !visited[nextx][nexty] && grid[nextx][nexty] == 1 { // 没有访问过的 同时 是陆地的
+			visited[nextx][nexty] = true
+			count++
+			dfs(grid, visited, nextx, nexty)
+		}
+	}
+}
+
+func main() {
+	var n, m int
+	fmt.Scan(&n, &m)
+
+	grid := make([][]int, n)
+	for i := 0; i < n; i++ {
+		grid[i] = make([]int, m)
+		for j := 0; j < m; j++ {
+			fmt.Scan(&grid[i][j])
+		}
+	}
+
+	visited := make([][]bool, n)
+	for i := 0; i < n; i++ {
+		visited[i] = make([]bool, m)
+	}
+
+	result := 0
+	for i := 0; i < n; i++ {
+		for j := 0; j < m; j++ {
+			if !visited[i][j] && grid[i][j] == 1 {
+				count = 1 // 因为dfs处理下一个节点，所以这里遇到陆地了就先计数，dfs处理接下来的相邻陆地
+				visited[i][j] = true
+				dfs(grid, visited, i, j)
+				if count > result {
+					result = count
+				}
+			}
+		}
+	}
+
+	fmt.Println(result)
+}
+
+
+
+```
+
+
+
 ### Rust

 ### Javascript
@@ -420,6 +486,65 @@ const bfs = (graph, visited, x, y) => {

 ### PhP

+``` php
+
+<?php
+
+function dfs(&$grid, &$visited, $x, $y, &$count, &$dir) {
+    for ($i = 0; $i < 4; $i++) {
+        $nextx = $x + $dir[$i][0];
+        $nexty = $y + $dir[$i][1];
+        if ($nextx < 0 || $nextx >= count($grid) || $nexty < 0 || $nexty >= count($grid[0])) continue;  // 越界了，直接跳过
+        if (!$visited[$nextx][$nexty] && $grid[$nextx][$nexty] == 1) { // 没有访问过的 同时 是陆地的
+            $visited[$nextx][$nexty] = true;
+            $count++;
+            dfs($grid, $visited, $nextx, $nexty, $count, $dir);
+        }
+    }
+}
+
+// Main function
+function main() {
+    $input = trim(fgets(STDIN));
+    list($n, $m) = explode(' ', $input);
+    
+    $grid = [];
+    for ($i = 0; $i < $n; $i++) {
+        $input = trim(fgets(STDIN));
+        $grid[] = array_map('intval', explode(' ', $input));
+    }
+    
+    $visited = [];
+    for ($i = 0; $i < $n; $i++) {
+        $visited[] = array_fill(0, $m, false);
+    }
+    
+    $result = 0;
+    $count = 0;
+    $dir = [[0, 1], [1, 0], [-1, 0], [0, -1]]; // 四个方向
+
+    for ($i = 0; $i < $n; $i++) {
+        for ($j = 0; $j < $m; $j++) {
+            if (!$visited[$i][$j] && $grid[$i][$j] == 1) {
+                $count = 1;  // 因为dfs处理下一个节点，所以这里遇到陆地了就先计数，dfs处理接下来的相邻陆地
+                $visited[$i][$j] = true;
+                dfs($grid, $visited, $i, $j, $count, $dir); // 将与其链接的陆地都标记上 true
+                $result = max($result, $count);
+            }
+        }
+    }
+    
+    echo $result . "\n";
+}
+
+main();
+
+?>
+
+
+```
+
+
 ### Swift

 ### Scala
--- a/problems/kamacoder/0101.孤岛的总面积.md
+++ b/problems/kamacoder/0101.孤岛的总面积.md
@@ -185,6 +185,77 @@ int main() {

 ### Java 

+``` java
+
+import java.util.*;
+
+public class Main {
+    private static int count = 0;
+    private static final int[][] dir = {{0, 1}, {1, 0}, {-1, 0}, {0, -1}}; // 四个方向
+
+    private static void bfs(int[][] grid, int x, int y) {
+        Queue<int[]> que = new LinkedList<>();
+        que.add(new int[]{x, y});
+        grid[x][y] = 0; // 只要加入队列，立刻标记
+        count++;
+        while (!que.isEmpty()) {
+            int[] cur = que.poll();
+            int curx = cur[0];
+            int cury = cur[1];
+            for (int i = 0; i < 4; i++) {
+                int nextx = curx + dir[i][0];
+                int nexty = cury + dir[i][1];
+                if (nextx < 0 || nextx >= grid.length || nexty < 0 || nexty >= grid[0].length) continue; // 越界了，直接跳过
+                if (grid[nextx][nexty] == 1) {
+                    que.add(new int[]{nextx, nexty});
+                    count++;
+                    grid[nextx][nexty] = 0; // 只要加入队列立刻标记
+                }
+            }
+        }
+    }
+
+    public static void main(String[] args) {
+        Scanner scanner = new Scanner(System.in);
+        int n = scanner.nextInt();
+        int m = scanner.nextInt();
+        int[][] grid = new int[n][m];
+        
+        // 读取网格
+        for (int i = 0; i < n; i++) {
+            for (int j = 0; j < m; j++) {
+                grid[i][j] = scanner.nextInt();
+            }
+        }
+        
+        // 从左侧边，和右侧边向中间遍历
+        for (int i = 0; i < n; i++) {
+            if (grid[i][0] == 1) bfs(grid, i, 0);
+            if (grid[i][m - 1] == 1) bfs(grid, i, m - 1);
+        }
+        
+        // 从上边和下边向中间遍历
+        for (int j = 0; j < m; j++) {
+            if (grid[0][j] == 1) bfs(grid, 0, j);
+            if (grid[n - 1][j] == 1) bfs(grid, n - 1, j);
+        }
+        
+        count = 0;
+        for (int i = 0; i < n; i++) {
+            for (int j = 0; j < m; j++) {
+                if (grid[i][j] == 1) bfs(grid, i, j);
+            }
+        }
+
+        System.out.println(count);
+    }
+}
+
+
+
+```
+
+
 ### Python
 ```python
 from collections import deque
@@ -238,6 +309,97 @@ print(count)
 ```
 ### Go

+``` go
+
+package main
+
+import (
+    "fmt"
+)
+
+var count int
+var dir = [4][2]int{{0, 1}, {1, 0}, {-1, 0}, {0, -1}} // 四个方向
+
+func bfs(grid [][]int, x, y int) {
+    queue := [][2]int{{x, y}}
+    grid[x][y] = 0 // 只要加入队列，立刻标记
+    count++
+    
+    for len(queue) > 0 {
+        cur := queue[0]
+        queue = queue[1:]
+        curx, cury := cur[0], cur[1]
+        
+        for i := 0; i < 4; i++ {
+            nextx := curx + dir[i][0]
+            nexty := cury + dir[i][1]
+            
+            if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {
+                continue // 越界了，直接跳过
+            }
+            
+            if grid[nextx][nexty] == 1 {
+                queue = append(queue, [2]int{nextx, nexty})
+                count++
+                grid[nextx][nexty] = 0 // 只要加入队列立刻标记
+            }
+        }
+    }
+}
+
+func main() {
+    var n, m int
+    fmt.Scan(&n, &m)
+    
+    grid := make([][]int, n)
+    for i := range grid {
+        grid[i] = make([]int, m)
+    }
+    
+    for i := 0; i < n; i++ {
+        for j := 0; j < m; j++ {
+            fmt.Scan(&grid[i][j])
+        }
+    }
+    
+    // 从左侧边，和右侧边向中间遍历
+    for i := 0; i < n; i++ {
+        if grid[i][0] == 1 {
+            bfs(grid, i, 0)
+        }
+        if grid[i][m-1] == 1 {
+            bfs(grid, i, m-1)
+        }
+    }
+    
+    // 从上边和下边向中间遍历
+    for j := 0; j < m; j++ {
+        if grid[0][j] == 1 {
+            bfs(grid, 0, j)
+        }
+        if grid[n-1][j] == 1 {
+            bfs(grid, n-1, j)
+        }
+    }
+    
+    // 清空之前的计数
+    count = 0
+    
+    // 遍历所有位置
+    for i := 0; i < n; i++ {
+        for j := 0; j < m; j++ {
+            if grid[i][j] == 1 {
+                bfs(grid, i, j)
+            }
+        }
+    }
+    
+    fmt.Println(count)
+}
+
+
+```
+
 ### Rust

 ### Javascript
--- a/problems/kamacoder/0103.水流问题.md
+++ b/problems/kamacoder/0103.水流问题.md
@@ -355,6 +355,62 @@ public class Main {
 ```

 ### Python
+```Python
+first = set()
+second = set()
+directions = [[-1, 0], [0, 1], [1, 0], [0, -1]]
+
+def dfs(i, j, graph, visited, side):
+    if visited[i][j]:
+        return
+    
+    visited[i][j] = True
+    side.add((i, j))
+    
+    for x, y in directions:
+        new_x = i + x
+        new_y = j + y
+        if (
+            0 <= new_x < len(graph)
+            and 0 <= new_y < len(graph[0])
+            and int(graph[new_x][new_y]) >= int(graph[i][j])
+        ):
+            dfs(new_x, new_y, graph, visited, side)
+
+def main():
+    global first
+    global second
+    
+    N, M = map(int, input().strip().split())
+    graph = []
+    for _ in range(N):
+        row = input().strip().split()
+        graph.append(row)
+    
+    # 是否可到达第一边界
+    visited = [[False] * M for _ in range(N)]
+    for i in range(M):
+        dfs(0, i, graph, visited, first)
+    for i in range(N):
+        dfs(i, 0, graph, visited, first)
+    
+    # 是否可到达第二边界
+    visited = [[False] * M for _ in range(N)]
+    for i in range(M):
+        dfs(N - 1, i, graph, visited, second)
+    for i in range(N):
+        dfs(i, M - 1, graph, visited, second)
+
+    # 可到达第一边界和第二边界
+    res = first & second
+    
+    for x, y in res:
+        print(f"{x} {y}")
+    
+    
+if __name__ == "__main__":
+    main()
+```

 ### Go

@@ -362,6 +418,350 @@ public class Main {

 ### Javascript

+#### 深搜
+
+```javascript
+const r1 = require('readline').createInterface({ input: process.stdin });
+// 创建readline接口
+let iter = r1[Symbol.asyncIterator]();
+// 创建异步迭代器
+const readline = async () => (await iter.next()).value;
+
+let graph // 地图
+let N, M // 地图大小
+const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
+
+
+// 读取输入，初始化地图
+const initGraph = async () => {
+  let line = await readline();
+  [N, M] = line.split(' ').map(Number);
+  graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
+
+  for (let i = 0; i < N; i++) {
+    line = await readline()
+    line = line.split(' ').map(Number)
+    for (let j = 0; j < M; j++) {
+      graph[i][j] = line[j]
+    }
+  }
+}
+
+
+/**
+ * @description: 从（x，y）开始深度优先遍历地图
+ * @param {*} graph 地图
+ * @param {*} visited 可访问节点
+ * @param {*} x 开始搜索节点的下标
+ * @param {*} y 开始搜索节点的下标
+ * @return {*}
+ */
+const dfs = (graph, visited, x, y) => {
+  if (visited[x][y]) return
+  visited[x][y] = true // 标记为可访问
+
+  for (let i = 0; i < 4; i++) {
+    let nextx = x + dir[i][0]
+    let nexty = y + dir[i][1]
+    if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界,跳过
+    if (graph[x][y] < graph[nextx][nexty]) continue //不能流过.跳过
+    dfs(graph, visited, nextx, nexty)
+  }
+}
+
+
+/**
+ * @description: 判断地图上的(x, y)是否可以到达第一组边界和第二组边界
+ * @param {*} x 坐标
+ * @param {*} y 坐标
+ * @return {*} true可以到达，false不可以到达
+ */
+const isResult = (x, y) => {
+  let visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
+
+  let isFirst = false //是否可到达第一边界
+  let isSecond = false //是否可到达第二边界
+
+  // 深搜，将(x, y)可到达的所有节点做标记
+  dfs(graph, visited, x, y)
+
+  // 判断能否到第一边界左边
+  for (let i = 0; i < N; i++) {
+    if (visited[i][0]) {
+      isFirst = true
+      break
+    }
+  }
+
+  // 判断能否到第一边界上边
+  for (let j = 0; j < M; j++) {
+    if (visited[0][j]) {
+      isFirst = true
+      break
+    }
+  }
+
+  // 判断能否到第二边界右边
+  for (let i = 0; i < N; i++) {
+    if (visited[i][M - 1]) {
+      isSecond = true
+      break
+    }
+  }
+
+  // 判断能否到第二边界下边
+  for (let j = 0; j < M; j++) {
+    if (visited[N - 1][j]) {
+      isSecond = true
+      break
+    }
+  }
+
+  return isFirst && isSecond
+}
+
+(async function () {
+
+  // 读取输入，初始化地图
+  await initGraph()
+
+  // 遍历地图，判断是否能到达第一组边界和第二组边界
+  for (let i = 0; i < N; i++) {
+    for (let j = 0; j < M; j++) {
+      if (isResult(i, j)) console.log(i + ' ' + j);
+    }
+  }
+})()
+```
+
+
+
+#### 广搜-解法一
+
+```java
+const r1 = require('readline').createInterface({ input: process.stdin });
+// 创建readline接口
+let iter = r1[Symbol.asyncIterator]();
+// 创建异步迭代器
+const readline = async () => (await iter.next()).value;
+
+let graph // 地图
+let N, M // 地图大小
+const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
+
+
+// 读取输入，初始化地图
+const initGraph = async () => {
+  let line = await readline();
+  [N, M] = line.split(' ').map(Number);
+  graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
+
+  for (let i = 0; i < N; i++) {
+    line = await readline()
+    line = line.split(' ').map(Number)
+    for (let j = 0; j < M; j++) {
+      graph[i][j] = line[j]
+    }
+  }
+}
+
+
+/**
+ * @description: 从（x，y）开始广度优先遍历地图
+ * @param {*} graph 地图
+ * @param {*} visited 可访问节点
+ * @param {*} x 开始搜索节点的下标
+ * @param {*} y 开始搜索节点的下标
+ * @return {*}
+ */
+const bfs = (graph, visited, x, y) => {
+  let queue = []
+  queue.push([x, y])
+  visited[x][y] = true
+
+  while (queue.length) {
+    const [xx, yy] = queue.shift()
+    for (let i = 0; i < 4; i++) {
+      let nextx = xx + dir[i][0]
+      let nexty = yy + dir[i][1]
+      if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
+
+      // 可访问或者不能流过, 跳过 (注意这里是graph[xx][yy] < graph[nextx][nexty], 不是graph[x][y] < graph[nextx][nexty])
+      if (visited[nextx][nexty] || graph[xx][yy] < graph[nextx][nexty]) continue
+
+      queue.push([nextx, nexty])
+      visited[nextx][nexty] = true
+
+    }
+  }
+}
+
+
+/**
+ * @description: 判断地图上的(x, y)是否可以到达第一组边界和第二组边界
+ * @param {*} x 坐标
+ * @param {*} y 坐标
+ * @return {*} true可以到达，false不可以到达
+ */
+const isResult = (x, y) => {
+  let visited = new Array(N).fill(false).map(() => new Array(M).fill(false))
+
+  let isFirst = false //是否可到达第一边界
+  let isSecond = false //是否可到达第二边界
+
+  // 深搜，将(x, y)可到达的所有节点做标记
+  bfs(graph, visited, x, y)
+
+  // console.log(visited);
+
+  // 判断能否到第一边界左边
+  for (let i = 0; i < N; i++) {
+    if (visited[i][0]) {
+      isFirst = true
+      break
+    }
+  }
+
+  // 判断能否到第一边界上边
+  for (let j = 0; j < M; j++) {
+    if (visited[0][j]) {
+      isFirst = true
+      break
+    }
+  }
+
+  // 判断能否到第二边界右边
+  for (let i = 0; i < N; i++) {
+    if (visited[i][M - 1]) {
+      isSecond = true
+      break
+    }
+  }
+
+  // 判断能否到第二边界下边
+  for (let j = 0; j < M; j++) {
+    if (visited[N - 1][j]) {
+      isSecond = true
+      break
+    }
+  }
+
+  return isFirst && isSecond
+}
+
+(async function () {
+
+  // 读取输入，初始化地图
+  await initGraph()
+
+  // 遍历地图，判断是否能到达第一组边界和第二组边界
+  for (let i = 0; i < N; i++) {
+    for (let j = 0; j < M; j++) {
+      if (isResult(i, j)) console.log(i + ' ' + j);
+    }
+  }
+})()
+```
+
+
+
+#### 广搜-解法二
+
+从第一边界和第二边界开始向高处流, 标记可以流到的位置, 两个边界都能到达的位置就是所求结果
+
+```javascript
+ const r1 = require('readline').createInterface({ input: process.stdin });
+ // 创建readline接口
+ let iter = r1[Symbol.asyncIterator]();
+ // 创建异步迭代器
+ const readline = async () => (await iter.next()).value;
+ 
+ let graph // 地图
+ let N, M // 地图大小
+ const dir = [[0, 1], [1, 0], [0, -1], [-1, 0]] //方向
+ 
+ 
+ // 读取输入，初始化地图
+ const initGraph = async () => {
+   let line = await readline();
+   [N, M] = line.split(' ').map(Number);
+   graph = new Array(N).fill(0).map(() => new Array(M).fill(0))
+ 
+   for (let i = 0; i < N; i++) {
+     line = await readline()
+     line = line.split(' ').map(Number)
+     for (let j = 0; j < M; j++) {
+       graph[i][j] = line[j]
+     }
+   }
+ }
+ 
+ 
+ /**
+  * @description: 从（x，y）开始广度优先遍历地图
+  * @param {*} graph 地图
+  * @param {*} visited 可访问节点
+  * @param {*} x 开始搜索节点的下标
+  * @param {*} y 开始搜索节点的下标
+  * @return {*}
+  */
+ const bfs = (graph, visited, x, y) => {
+   if(visited[x][y]) return
+   
+   let queue = []
+   queue.push([x, y])
+   visited[x][y] = true
+ 
+   while (queue.length) {
+     const [xx, yy] = queue.shift()
+     for (let i = 0; i < 4; i++) {
+       let nextx = xx + dir[i][0]
+       let nexty = yy + dir[i][1]
+       if (nextx < 0 || nextx >= N || nexty < 0 || nexty >= M) continue //越界, 跳过
+ 
+       // 可访问或者不能流过, 跳过 (注意因为是从边界往高处流, 所以这里是graph[xx][yy] >= graph[nextx][nexty], 还要注意不是graph[xx][yy] >= graph[nextx][nexty])
+       if (visited[nextx][nexty] || graph[xx][yy] >= graph[nextx][nexty]) continue
+ 
+       queue.push([nextx, nexty])
+       visited[nextx][nexty] = true
+     }
+   }
+ }
+ 
+ (async function () {
+ 
+   // 读取输入，初始化地图
+   await initGraph()
+ 
+   // 记录第一边界可到达的节点
+   let firstBorder = new Array(N).fill(false).map(() => new Array(M).fill(false))
+ 
+   // 记录第二边界可到达的节点
+   let secondBorder = new Array(N).fill(false).map(() => new Array(M).fill(false))
+ 
+   // 第一边界左边和第二边界右边
+   for (let i = 0; i < N; i++) {
+     bfs(graph, firstBorder, i, 0)
+     bfs(graph, secondBorder, i, M - 1)
+   }
+ 
+   // 第一边界上边和第二边界下边
+   for (let j = 0; j < M; j++) {
+     bfs(graph, firstBorder, 0, j)
+     bfs(graph, secondBorder, N - 1, j)
+   }
+ 
+   // 遍历地图，判断是否能到达第一组边界和第二组边界
+   for (let i = 0; i < N; i++) {
+     for (let j = 0; j < M; j++) {
+       if (firstBorder[i][j] && secondBorder[i][j]) console.log(i + ' ' + j);
+     }
+   }
+ })()
+```
+
+
+
 ### TypeScript

 ### PhP
--- a/problems/kamacoder/0104.建造最大岛屿.md
+++ b/problems/kamacoder/0104.建造最大岛屿.md
@@ -366,6 +366,79 @@ public class Main {

 ### Python

+```Python
+import collections
+
+directions = [[-1, 0], [0, 1], [0, -1], [1, 0]]
+area = 0
+
+def dfs(i, j, grid, visited, num):
+    global area
+    
+    if visited[i][j]:
+        return
+
+    visited[i][j] = True
+    grid[i][j] = num  # 标记岛屿号码
+    area += 1
+    
+    for x, y in directions:
+        new_x = i + x
+        new_y = j + y
+        if (
+            0 <= new_x < len(grid)
+            and 0 <= new_y < len(grid[0])
+            and grid[new_x][new_y] == "1"
+        ):
+            dfs(new_x, new_y, grid, visited, num)
+    
+
+def main():
+    global area
+    
+    N, M = map(int, input().strip().split())
+    grid = []
+    for i in range(N):
+        grid.append(input().strip().split())
+    visited = [[False] * M for _ in range(N)]
+    rec = collections.defaultdict(int)
+    
+    cnt = 2
+    for i in range(N):
+        for j in range(M):
+            if grid[i][j] == "1":
+                area = 0
+                dfs(i, j, grid, visited, cnt)
+                rec[cnt] = area  # 纪录岛屿面积
+                cnt += 1
+    
+    res = 0
+    for i in range(N):
+        for j in range(M):
+            if grid[i][j] == "0":
+                max_island = 1  # 将水变为陆地，故从1开始计数
+                v = set()
+                for x, y in directions:
+                    new_x = i + x
+                    new_y = j + y
+                    if (
+                        0 <= new_x < len(grid)
+                        and 0 <= new_y < len(grid[0])
+                        and grid[new_x][new_y] != "0"
+                        and grid[new_x][new_y] not in v  # 岛屿不可重复
+                    ):
+                        max_island += rec[grid[new_x][new_y]]
+                        v.add(grid[new_x][new_y])
+                res = max(res, max_island)
+
+    if res == 0:
+        return max(rec.values())  # 无水的情况
+    return res
+    
+if __name__ == "__main__":
+    print(main())
+```
+
 ### Go

 ### Rust
--- a/problems/kamacoder/0107.寻找存在的路径.md
+++ b/problems/kamacoder/0107.寻找存在的路径.md
@@ -158,7 +158,62 @@ int main() {

 ## 其他语言版本

-### Java 
+### Java
+
+```Java
+
+import java.util.*;
+ 
+public class Main{
+    public static void main(String[] args) {
+        int N, M;
+        Scanner scanner = new Scanner(System.in);
+        N = scanner.nextInt();
+        M = scanner.nextInt();
+        DisJoint disJoint = new DisJoint(N + 1);
+        for (int i = 0; i < M; ++i) {
+            disJoint.join(scanner.nextInt(), scanner.nextInt());
+        }
+        if(disJoint.isSame(scanner.nextInt(), scanner.nextInt())) {
+            System.out.println("1");
+        } else {
+            System.out.println("0");
+        }
+    }
+ 
+}
+
+//并查集模板
+class DisJoint{
+    private int[] father;
+ 
+    public DisJoint(int N) {
+        father = new int[N];
+        for (int i = 0; i < N; ++i){
+            father[i] = i;
+        }
+    }
+ 
+    public int find(int n) {
+        return n == father[n] ? n : (father[n] = find(father[n]));
+    }
+ 
+    public void join (int n, int m) {
+        n = find(n);
+        m = find(m);
+        if (n == m) return;
+        father[m] = n;
+    }
+ 
+    public boolean isSame(int n, int m){
+        n = find(n);
+        m = find(m);
+        return n == m;
+    }
+ 
+}
+
+```

 ### Python

--- a/problems/kamacoder/0108.冗余连接.md
+++ b/problems/kamacoder/0108.冗余连接.md
@@ -141,6 +141,70 @@ int main() {

 ### Javascript

+```javascript
+const r1 = require('readline').createInterface({ input: process.stdin });
+// 创建readline接口
+let iter = r1[Symbol.asyncIterator]();
+// 创建异步迭代器
+const readline = async () => (await iter.next()).value;
+
+
+let N // 节点数和边数
+let father = []  // 并查集
+
+
+// 并查集初始化
+const init = () => {
+  for (let i = 1; i <= N; i++)  father[i] = i;
+}
+
+// 并查集里寻根的过程
+const find = (u) => {
+  return u == father[u] ? u : father[u] = find(father[u])
+}
+
+// 将v->u 这条边加入并查集
+const join = (u, v) => {
+  u = find(u)
+  v = find(v)
+  if (u == v) return // 如果发现根相同，则说明在一个集合，不用两个节点相连直接返回
+  father[v] = u
+}
+
+// 判断 u 和 v是否找到同一个根
+const isSame = (u, v) => {
+  u = find(u)
+  v = find(v)
+  return u == v
+}
+
+
+(async function () {
+  // 读取第一行输入
+  let line = await readline();
+  N = Number(line);
+
+  // 初始化并查集
+  father = new Array(N)
+  init()
+
+  // 读取边信息, 加入并查集
+  for (let i = 0; i < N; i++) {
+    line = await readline()
+    line = line.split(' ').map(Number)
+
+    if (!isSame(line[0], line[1])) {
+      join(line[0], line[1])
+    }else{
+      console.log(line[0], line[1]);
+      break
+    }
+  }
+})()
+```
+
+
+
 ### TypeScript

 ### PhP
--- a/problems/kamacoder/0109.冗余连接II.md
+++ b/problems/kamacoder/0109.冗余连接II.md
@@ -78,7 +78,7 @@

 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527120531.png)

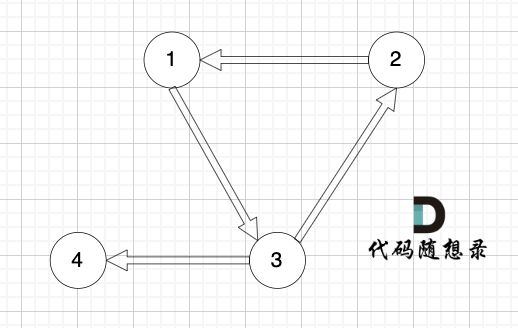
-对于情况二，删掉构成环的边就可以了。 
+对于情况三，删掉构成环的边就可以了。 


 ## 写代码
@@ -225,6 +225,7 @@ int main() {
            vec.push_back(i);
        }
    }
+    // 情况一、情况二
    if (vec.size() > 0) {
        // 放在vec里的边已经按照倒叙放的，所以这里就优先删vec[0]这条边
        if (isTreeAfterRemoveEdge(edges, vec[0])) {
--- a/problems/kamacoder/0110.字符串接龙.md
+++ b/problems/kamacoder/0110.字符串接龙.md
@@ -217,6 +217,38 @@ public class Main {
 ```

 ### Python
+```Python
+def judge(s1,s2):
+    count=0
+    for i in range(len(s1)):
+        if s1[i]!=s2[i]:
+            count+=1
+    return count==1
+
+if __name__=='__main__':
+    n=int(input())
+    beginstr,endstr=map(str,input().split())
+    if beginstr==endstr:
+        print(0)
+        exit()
+    strlist=[]
+    for i in range(n):
+        strlist.append(input())
+    
+    # use bfs
+    visit=[False for i in range(n)]
+    queue=[[beginstr,1]]
+    while queue:
+        str,step=queue.pop(0)
+        if judge(str,endstr):
+            print(step+1)
+            exit()
+        for i in range(n):
+            if visit[i]==False and judge(strlist[i],str):
+                visit[i]=True
+                queue.append([strlist[i],step+1])
+    print(0)
+```

 ### Go

--- a/problems/kamacoder/0113.国际象棋.md
+++ b/problems/kamacoder/0113.国际象棋.md
@@ -0,0 +1,59 @@
+
+# 113.国际象棋
+
+广搜，但本题如果广搜枚举马和象的话会超时。 
+
+广搜要只枚举马的走位，同时判断是否在对角巷直接走象
+
+```CPP 
+#include <iostream>
+using namespace std;
+const int N = 100005, mod = 1000000007;
+using ll = long long;
+int n, ans;
+int dir[][2] = {{1, 2}, {1, -2}, {-1, 2}, {-1, -2}, {2, 1}, {2, -1}, {-2, -1}, {-2, 1}};
+int main() {
+    int x1, y1, x2, y2;
+    cin >> n;
+    while (n--) {
+        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
+        if (x1 == x2 && y1 == y2) {
+            cout << 0 << endl;
+            continue;
+        }
+        // 判断象走一步到达
+        int d = abs(x1 - x2) - abs(y1 - y2);
+        if (!d) {cout << 1 << endl; continue;}
+        // 判断马走一步到达
+        bool one = 0;
+        for (int i = 0; i < 8; ++i) {
+            int dx = x1 + dir[i][0], dy = y1 + dir[i][1];
+            if (dx == x2 && dy == y2) {
+                cout << 1 << endl;
+                one = true;
+                break;
+            }
+        }
+        if (one) continue;
+        // 接下来为两步的逻辑, 象走两步或者马走一步,象走一步
+        // 象直接两步可以到达,这个计算是不是同颜色的格子,象可以在两步到达所有同颜色的格子
+        int d2 = abs(x1 - x2) + abs(y1 - y2);
+        if (d2 % 2 == 0) {
+            cout << 2 << endl;
+            continue;
+        }
+        // 接下来判断马 + 象的组合
+        bool two = 0;
+        for (int i = 0; i < 8; ++i) {
+            int dx = x1 + dir[i][0], dy = y1 + dir[i][1];
+            int d = abs(dx - x2) - abs(dy - y2);
+            if (!d) {cout << 2 << endl; two = true; break;}
+        }
+        if (two) continue;
+        // 剩下的格子全都是三步到达的
+        cout << 3 << endl;
+    }
+    return 0;
+}
+
+```
--- a/problems/kamacoder/0117.软件构建.md
+++ b/problems/kamacoder/0117.软件构建.md
@@ -193,7 +193,7 @@

 理解思想后，确实不难，但代码写起来也不容易。 

-为了每次可以找到所有节点的入度信息，我们要在初始话的时候，就把每个节点的入度 和 每个节点的依赖关系做统计。 
+为了每次可以找到所有节点的入度信息，我们要在初始化的时候，就把每个节点的入度 和 每个节点的依赖关系做统计。 

 代码如下： 

@@ -451,6 +451,80 @@ if __name__ == "__main__":

 ### Javascript

+```javascript
+const r1 = require('readline').createInterface({ input: process.stdin });
+// 创建readline接口
+let iter = r1[Symbol.asyncIterator]();
+// 创建异步迭代器
+const readline = async () => (await iter.next()).value;
+
+
+let N, M // 节点数和边数
+let inDegrees = [] // 入度
+let umap = new Map() // 记录文件依赖关系
+let result = [] // 结果
+
+
+// 根据输入, 初始化数据
+const init = async () => {
+  // 读取第一行输入
+  let line = await readline();
+  [N, M] = line.split(' ').map(Number)
+
+  inDegrees = new Array(N).fill(0)
+
+  // 读取边集
+  while (M--) {
+    line = await readline();
+    let [x, y] = line.split(' ').map(Number)
+
+    // 记录入度
+    inDegrees[y]++
+
+    // 记录x指向哪些文件
+    if (!umap.has(x)) {
+      umap.set(x, [y])
+    } else {
+      umap.get(x).push(y)
+    }
+  }
+}
+
+(async function () {
+  // 根据输入, 初始化数据
+  await init()
+
+  let queue = [] // 入度为0的节点
+  for (let i = 0; i < N; i++) {
+    if (inDegrees[i] == 0) {
+      queue.push(i)
+    }
+  }
+
+  while (queue.length) {
+    let cur = queue.shift() //当前文件
+
+    result.push(cur)
+
+    let files = umap.get(cur) // 当前文件指向的文件
+
+    // 当前文件指向的文件入度减1
+    if (files && files.length) {
+      for (let i = 0; i < files.length; i++) {
+        inDegrees[files[i]]--
+        if (inDegrees[files[i]] == 0) queue.push(files[i])
+      }
+    }
+  }
+
+  // 这里result.length == N 一定要判断, 因为可能存在环
+  if (result.length == N) return console.log(result.join(' '))
+  console.log(-1)
+})()
+```
+
+
+
 ### TypeScript

 ### PhP
--- a/problems/kamacoder/0121.小红的区间翻转.md
+++ b/problems/kamacoder/0121.小红的区间翻转.md
@@ -0,0 +1,132 @@
+
+# 121. 小红的区间翻转
+
+比较暴力的方式，就是直接模拟， 枚举所有 区间，然后检查其翻转的情况。 
+
+在检查翻转的时候，需要一些代码优化，否则容易超时。
+
+```CPP 
+#include <iostream>
+#include <vector>
+using namespace std;
+
+bool canTransform(const vector<int>& a, const vector<int>& b, int left, int right) {
+    // 提前检查翻转区间的值是否可以匹配
+    for (int i = left, j = right; i <= right; i++, j--) {
+        if (a[i] != b[j]) {
+            return false;
+        }
+    }
+    // 检查翻转区间外的值是否匹配
+    for (int i = 0; i < left; i++) {
+        if (a[i] != b[i]) {
+            return false;
+        }
+    }
+    for (int i = right + 1; i < a.size(); i++) {
+        if (a[i] != b[i]) {
+            return false;
+        }
+    }
+    return true;
+}
+
+int main() {
+    int n;
+    cin >> n;
+
+    vector<int> a(n);
+    vector<int> b(n);
+
+    for (int i = 0; i < n; i++) {
+        cin >> a[i];
+    }
+
+    for (int i = 0; i < n; i++) {
+        cin >> b[i];
+    }
+
+    int count = 0;
+
+    // 遍历所有可能的区间
+    for (int left = 0; left < n; left++) {
+        for (int right = left; right < n; right++) {
+            // 检查翻转区间 [left, right] 后，a 是否可以变成 b
+            if (canTransform(a, b, left, right)) {
+                count++;
+            }
+        }
+    }
+    cout << count << endl;
+    return 0;
+}
+```
+
+也可以事先计算好，最长公共前缀，和最长公共后缀。 
+
+在公共前缀和公共后缀之间的部分进行翻转操作，这样我们可以减少很多不必要的翻转尝试。 
+
+通过在公共前缀和后缀之间的部分，找到可以通过翻转使得 a 和 b 相等的区间。 
+
+以下 为评论区 卡码网用户：码鬼的C++代码 
+
+```CPP 
+#include <iostream>
+#include <vector>
+
+using namespace std;
+
+int main() {
+    int n;
+    cin >> n;
+    vector<int> a(n), b(n);
+    for (int i = 0; i < n; i++) {
+        cin >> a[i];
+    }
+    for (int i = 0; i < n; i++) {
+        cin >> b[i];
+    }
+
+    vector<int> prefix(n, 0), suffix(n, 0);
+    
+    // 计算前缀相等的位置
+    int p = 0;
+    while (p < n && a[p] == b[p]) {
+        prefix[p] = 1;
+        p++;
+    }
+
+    // 计算后缀相等的位置
+    int s = n - 1;
+    while (s >= 0 && a[s] == b[s]) {
+        suffix[s] = 1;
+        s--;
+    }
+
+    int count = 0;
+
+    // 遍历所有可能的区间
+    for (int i = 0; i < n - 1; i++) {
+        for (int j = i + 1; j < n; j++) {
+            // 判断前缀和后缀是否相等
+            if ((i == 0 || prefix[i - 1] == 1) && (j == n - 1 || suffix[j + 1] == 1)) {
+                // 判断翻转后的子数组是否和目标数组相同
+                bool is_palindrome = true;
+                for (int k = 0; k <= (j - i) / 2; k++) {
+                    if (a[i + k] != b[j - k]) {
+                        is_palindrome = false;
+                        break;
+                    }
+                }
+                if (is_palindrome) {
+                    count++;
+                }
+            }
+        }
+    }
+
+    cout << count << endl;
+
+    return 0;
+}
+```
--- a/problems/kamacoder/0142.两个字符串的最小ASCII删除总和.md
+++ b/problems/kamacoder/0142.两个字符串的最小ASCII删除总和.md
@@ -0,0 +1,108 @@
+
+# 142. 两个字符串的最小 ASCII 删除总和
+
+本题和[代码随想录：两个字符串的删除操作](https://www.programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html) 思路基本是一样的。 
+
+属于编辑距离问题，如果想彻底了解，建议看看「代码随想录」的编辑距离总结篇。
+
+本题dp数组含义： 
+
+dp[i][j] 表示 以i-1为结尾的字符串word1，和以j-1位结尾的字符串word2，想要达到相等，所需要删除元素的最小ASCII 删除总和。  
+
+如果 s1[i - 1] 与 s2[j - 1] 相同，则不用删：`dp[i][j] = dp[i - 1][j - 1]` 
+
+如果 s1[i - 1] 与 s2[j - 1] 不相同，删word1 的 最小删除和： `dp[i - 1][j] + s1[i - 1]` ，删word2的最小删除和： `dp[i][j - 1] + s2[j - 1]` 
+
+取最小值： `dp[i][j] = min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1])`
+
+
+
+```CPP 
+#include <iostream>
+#include <vector>
+using namespace std;
+int main() {
+    string s1, s2;
+    cin >> s1 >> s2;
+    vector<vector<int>> dp(s1.size() + 1, vector<int>(s2.size() + 1, 0));
+
+    // s1 如果变成空串的最小删除ASCLL值综合
+    for (int i = 1; i <= s1.size(); i++) dp[i][0] = dp[i - 1][0] + s1[i - 1];
+    // s2 如果变成空串的最小删除ASCLL值综合
+    for (int j = 1; j <= s2.size(); j++) dp[0][j] = dp[0][j - 1] + s2[j - 1];
+
+    for (int i = 1; i <= s1.size(); i++) {
+        for (int j = 1; j <= s2.size(); j++) {
+            if (s1[i - 1] == s2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
+            else dp[i][j] = min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1]);
+        }
+    }
+    cout << dp[s1.size()][s2.size()] << endl;
+}
+```
+
+### Java 
+
+```Java 
+import java.util.Scanner;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner scanner = new Scanner(System.in);
+        String s1 = scanner.nextLine();
+        String s2 = scanner.nextLine();
+        int[][] dp = new int[s1.length() + 1][s2.length() + 1];
+
+        // s1 如果变成空串的最小删除ASCII值综合
+        for (int i = 1; i <= s1.length(); i++) {
+            dp[i][0] = dp[i - 1][0] + s1.charAt(i - 1);
+        }
+        // s2 如果变成空串的最小删除ASCII值综合
+        for (int j = 1; j <= s2.length(); j++) {
+            dp[0][j] = dp[0][j - 1] + s2.charAt(j - 1);
+        }
+
+        for (int i = 1; i <= s1.length(); i++) {
+            for (int j = 1; j <= s2.length(); j++) {
+                if (s1.charAt(i - 1) == s2.charAt(j - 1)) {
+                    dp[i][j] = dp[i - 1][j - 1];
+                } else {
+                    dp[i][j] = Math.min(dp[i - 1][j] + s1.charAt(i - 1), dp[i][j - 1] + s2.charAt(j - 1));
+                }
+            }
+        }
+        System.out.println(dp[s1.length()][s2.length()]);
+        scanner.close();
+    }
+}
+
+
+```
+
+### python 
+
+```python 
+def min_delete_sum(s1: str, s2: str) -> int:
+    dp = [[0] * (len(s2) + 1) for _ in range(len(s1) + 1)]
+
+    # s1 如果变成空串的最小删除ASCII值综合
+    for i in range(1, len(s1) + 1):
+        dp[i][0] = dp[i - 1][0] + ord(s1[i - 1])
+    # s2 如果变成空串的最小删除ASCII值综合
+    for j in range(1, len(s2) + 1):
+        dp[0][j] = dp[0][j - 1] + ord(s2[j - 1])
+
+    for i in range(1, len(s1) + 1):
+        for j in range(1, len(s2) + 1):
+            if s1[i - 1] == s2[j - 1]:
+                dp[i][j] = dp[i - 1][j - 1]
+            else:
+                dp[i][j] = min(dp[i - 1][j] + ord(s1[i - 1]), dp[i][j - 1] + ord(s2[j - 1]))
+
+    return dp[len(s1)][len(s2)]
+
+if __name__ == "__main__":
+    s1 = input().strip()
+    s2 = input().strip()
+    print(min_delete_sum(s1, s2))
+```
--- a/problems/kamacoder/0143.最长同值路径.md
+++ b/problems/kamacoder/0143.最长同值路径.md
@@ -0,0 +1,237 @@
+
+
+# 143. 最长同值路径 
+
+
+本题两个考点：
+
+1. 层序遍历构造二叉树 
+2. 树形dp，找出最长路径 
+
+对于写代码不多，或者动手能力比较差的录友，第一个 构造二叉树 基本就被卡主了。 
+
+```CPP
+#include <iostream>
+#include <queue>
+#include <vector>
+
+using namespace std;
+
+// 定义二叉树节点结构
+struct TreeNode {
+    int val;
+    TreeNode* left;
+    TreeNode* right;
+    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
+};
+
+// 根据层序遍历数组构建二叉树
+TreeNode* constructBinaryTree(const vector<string>& levelOrder) {
+    if (levelOrder.empty()) return NULL;
+
+    TreeNode* root = new TreeNode(stoi(levelOrder[0]));
+    queue<TreeNode*> q;
+    q.push(root);
+    int i = 1;
+
+    while (!q.empty() && i < levelOrder.size()) {
+        TreeNode* current = q.front();
+        q.pop();
+
+        if (i < levelOrder.size() && levelOrder[i] != "null") {
+            current->left = new TreeNode(stoi(levelOrder[i]));
+            q.push(current->left);
+        }
+        i++;
+
+        if (i < levelOrder.size() && levelOrder[i] != "null") {
+            current->right = new TreeNode(stoi(levelOrder[i]));
+            q.push(current->right);
+        }
+        i++;
+    }
+
+    return root;
+}
+
+int result = 0;
+
+// 树形DP
+int dfs(TreeNode* node) {
+    if (node == NULL) return 0;
+    int leftPath = dfs(node->left);
+    int rightPath = dfs(node->right);
+
+    int leftNum = 0, rightNum = 0;
+    if (node->left != NULL && node->left->val == node->val) {
+        leftNum = leftPath + 1;
+    }
+    if (node->right != NULL && node->right->val == node->val) {
+        rightNum = rightPath + 1;
+    }
+    result = max(result, leftNum + rightNum);
+    return max(leftNum, rightNum);
+
+}
+
+
+int main() {
+    int n;
+    cin >> n;
+    vector<string> levelOrder(n);
+    for (int i = 0; i < n ; i++) cin >> levelOrder[i];
+
+    TreeNode* root = constructBinaryTree(levelOrder);
+    dfs(root);
+    cout << result << endl;
+
+    return 0;
+}
+```
+
+### Java 
+
+```Java 
+import java.util.*;
+
+class TreeNode {
+    int val;
+    TreeNode left, right;
+    TreeNode(int x) {
+        val = x;
+        left = null;
+        right = null;
+    }
+}
+
+public class Main {
+    public static int result = 0;
+
+    public static TreeNode constructBinaryTree(List<String> levelOrder) {
+        if (levelOrder.isEmpty()) return null;
+
+        TreeNode root = new TreeNode(Integer.parseInt(levelOrder.get(0)));
+        Queue<TreeNode> queue = new LinkedList<>();
+        queue.add(root);
+        int i = 1;
+
+        while (!queue.isEmpty() && i < levelOrder.size()) {
+            TreeNode current = queue.poll();
+
+            if (i < levelOrder.size() && !levelOrder.get(i).equals("null")) {
+                current.left = new TreeNode(Integer.parseInt(levelOrder.get(i)));
+                queue.add(current.left);
+            }
+            i++;
+
+            if (i < levelOrder.size() && !levelOrder.get(i).equals("null")) {
+                current.right = new TreeNode(Integer.parseInt(levelOrder.get(i)));
+                queue.add(current.right);
+            }
+            i++;
+        }
+
+        return root;
+    }
+
+    public static int dfs(TreeNode node) {
+        if (node == null) return 0;
+        int leftPath = dfs(node.left);
+        int rightPath = dfs(node.right);
+
+        int leftNum = 0, rightNum = 0;
+        if (node.left != null && node.left.val == node.val) {
+            leftNum = leftPath + 1;
+        }
+        if (node.right != null && node.right.val == node.val) {
+            rightNum = rightPath + 1;
+        }
+        result = Math.max(result, leftNum + rightNum);
+        return Math.max(leftNum, rightNum);
+    }
+
+    public static void main(String[] args) {
+        Scanner sc = new Scanner(System.in);
+        int n = sc.nextInt();
+        sc.nextLine();  // consume the newline character
+        List<String> levelOrder = new ArrayList<>();
+        for (int i = 0; i < n; i++) {
+            levelOrder.add(sc.next());
+        }
+        TreeNode root = constructBinaryTree(levelOrder);
+        dfs(root);
+        System.out.println(result);
+        sc.close();
+    }
+}
+ 
+```
+
+### python 
+
+```python 
+from typing import List, Optional
+from collections import deque
+import sys
+
+class TreeNode:
+    def __init__(self, val: int = 0, left: 'TreeNode' = None, right: 'TreeNode' = None):
+        self.val = val
+        self.left = left
+        self.right = right
+
+def construct_binary_tree(level_order: List[str]) -> Optional[TreeNode]:
+    if not level_order:
+        return None
+
+    root = TreeNode(int(level_order[0]))
+    queue = deque([root])
+    i = 1
+
+    while queue and i < len(level_order):
+        current = queue.popleft()
+
+        if i < len(level_order) and level_order[i] != "null":
+            current.left = TreeNode(int(level_order[i]))
+            queue.append(current.left)
+        i += 1
+
+        if i < len(level_order) and level_order[i] != "null":
+            current.right = TreeNode(int(level_order[i]))
+            queue.append(current.right)
+        i += 1
+
+    return root
+
+result = 0
+
+def dfs(node: Optional[TreeNode]) -> int:
+    global result
+    if node is None:
+        return 0
+
+    left_path = dfs(node.left)
+    right_path = dfs(node.right)
+
+    left_num = right_num = 0
+    if node.left is not None and node.left.val == node.val:
+        left_num = left_path + 1
+    if node.right is not None and node.right.val == node.val:
+        right_num = right_path + 1
+
+    result = max(result, left_num + right_num)
+    return max(left_num, right_num)
+
+if __name__ == "__main__":
+    input = sys.stdin.read
+    data = input().strip().split()
+
+    n = int(data[0])
+    level_order = data[1:]
+
+    root = construct_binary_tree(level_order)
+    dfs(root)
+    print(result)
+
+
+```
--- a/problems/kamacoder/0144.字典序最小的01字符串.md
+++ b/problems/kamacoder/0144.字典序最小的01字符串.md
@@ -0,0 +1,66 @@
+
+# 0144.字典序最小的01字符串 
+
+贪心思路：移动尽可能 移动前面的1 ，这样可以是 字典序最小
+
+从前到后遍历，遇到 0 ，就用前面的 1 来交换
+
+```CPP
+#include <iostream>
+#include <string>
+using namespace std;
+int main() {
+    int n,k;
+    cin >> n >> k;
+    string s;
+    cin >> s;
+    for(int i = 0; i < n && k > 0; i++) {
+        if(s[i] == '0') {
+            // 开始用前面的 1  来交换
+            int j = i;
+            while(j > 0 && s[j - 1] == '1' && k > 0) {
+                swap(s[j], s[j - 1]);
+                --j;
+                --k;
+            }
+        }
+    }
+    cout << s << endl;
+    return 0;
+}
+
+```
+
+Java：
+
+```Java 
+
+import java.util.*;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner scanner = new Scanner(System.in);
+        int n = scanner.nextInt();
+        int k = scanner.nextInt();
+        scanner.nextLine(); // 消耗掉换行符
+        String s = scanner.nextLine();
+        char[] ch = s.toCharArray();
+
+        for (int i = 0; i < n && k > 0; i++) {
+            if (ch[i] == '0') {
+                // 开始用前面的 1 来交换
+                int j = i;
+                while (j > 0 && ch[j - 1] == '1' && k > 0) {
+                    char tmp = ch[j];
+                    ch[j] = ch[j - 1];
+                    ch[j - 1] = tmp;
+                    j--;
+                    k--;
+                }
+            }
+        }
+
+        System.out.println(new String(ch));
+    }
+} 
+```
--- a/problems/kamacoder/0145.数组子序列的排列.md
+++ b/problems/kamacoder/0145.数组子序列的排列.md
@@ -0,0 +1,98 @@
+
+# 145. 数组子序列的排列 
+
+每个元素出现的次数相乘就可以了。 
+
+注意 “长度为 m 的数组，1 到 m 每个元素都出现过，且恰好出现 1 次。” ，题目中有n个元素，所以我们要统计的就是 1 到 n 元素出现的个数。 
+
+因为如果有一个元素x 大于n了， 那不可能出现 长度为x的数组 且 1 到 x 每个元素都出现过。
+
+```CPP
+#include "bits/stdc++.h"
+using namespace std;
+int main(){
+    int n;
+    int x;
+    cin >> n;
+    unordered_map<int, int> umap;
+    for(int i = 0; i < n; ++i){
+        cin >> x;
+        if(umap.find(x) != umap.end()) umap[x]++;
+        else umap[x] = 1;
+    }
+    long long res = 0;
+    long long num = 1;
+    for (int i = 1; i <= n; i++) { 
+        if (umap.find(i) == umap.end()) break; // 如果i都没出现，后面得数也不能 1 到 m 每个元素都出现过
+        num = (num * umap[i]) % 1000000007;
+        res += num;
+        res %= 1000000007;
+    }
+    cout << res << endl;
+}
+
+```
+
+```Java 
+
+import java.util.HashMap;
+import java.util.Map;
+import java.util.Scanner;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner sc = new Scanner(System.in);
+        int n = sc.nextInt();
+        Map<Integer, Integer> map = new HashMap<>();
+        for (int i = 0; i < n; i++) {
+            int x = sc.nextInt();
+            map.put(x, map.getOrDefault(x, 0) + 1);
+        }
+        long res = 0;
+        long num = 1;
+        for (int i = 1; i <= n; i++) {
+            if (!map.containsKey(i)) break; // 如果i都没出现，后面得数也不能1到m每个元素都出现过
+            num = (num * map.get(i)) % 1000000007;
+            res += num;
+            res %= 1000000007;
+        }
+        System.out.println(res);
+        sc.close();
+    }
+}
+ 
+``` 
+
+
+```python 
+def main():
+    import sys
+    input = sys.stdin.read
+    data = input().split()
+
+    n = int(data[0])
+    umap = {}
+
+    for i in range(1, n + 1):
+        x = int(data[i])
+        if x in umap:
+            umap[x] += 1
+        else:
+            umap[x] = 1
+
+    res = 0
+    num = 1
+    MOD = 1000000007
+
+    for i in range(1, n + 1):
+        if i not in umap:
+            break  # 如果i都没出现，后面得数也不能1到m每个元素都出现过
+        num = (num * umap[i]) % MOD
+        res = (res + num) % MOD
+
+    print(res)
+
+if __name__ == "__main__":
+    main()
+
+```
--- a/problems/kamacoder/0146.传送树.md
+++ b/problems/kamacoder/0146.传送树.md
@@ -0,0 +1,65 @@
+
+
+
+
+# 146. 传送树 
+
+本题题意是比较绕的，我后面给补上了 【提示信息】对 题目输出样例讲解一下，相对会容易理解的多。
+
+```CPP 
+#include <iostream>
+#include <vector>
+#include <algorithm>
+using namespace std;
+
+vector<vector<int>> edge; // 邻接表来存图
+vector<int> nxt;
+int n;
+
+/*
+ * 递归函数，用于找到每个节点的下一个传送门节点，并记录在nxt数组中。
+ * 遍历当前节点的所有子节点，递归调用findNext以确保子节点的nxt值已经计算出来。
+ * 更新当前节点的nxt值为其子节点中编号最小的节点。
+ * 如果当前节点是叶子节点（即没有子节点），则将其nxt值设置为自身。
+ */
+void findNext(int node) {
+    for (int v : edge[node]) {
+        findNext(v);
+        if (nxt[node] == -1 || nxt[node] > min(v, nxt[v])) {
+            nxt[node] = min(v, nxt[v]);
+        }
+    }
+
+    // 叶子节点
+    if (nxt[node] == -1) {
+        nxt[node] = node;
+    }
+}
+
+// 计算从节点u出发经过若干次传送门到达叶子节点所需的步数。
+// 通过不断访问nxt节点，直到到达叶子节点，记录访问的节点数。
+int get(int u) {
+    int cnt = 1;
+    while (nxt[u] != u) {
+        cnt++;
+        u = nxt[u];
+    }
+    return cnt;
+}
+
+int main() {
+    cin >> n;
+    edge.resize(n + 1);
+    nxt.resize(n + 1, -1);
+    for (int i = 1; i <= n; ++i) {
+        int a, b;
+        cin >> a >> b;
+        edge[a].push_back(b);
+    }
+    findNext(1);
+    for (int i = 1; i <= n; ++i) {
+        cout << get(i) << ' ';
+    }
+}
+
+```
--- a/problems/kamacoder/0147.三珠互斥.md
+++ b/problems/kamacoder/0147.三珠互斥.md
@@ -0,0 +1,78 @@
+
+# 三珠互斥 
+
+1. 如果k * 3 大于 n 了，那说明一定没结果，如果没想明白，大家举个例子试试看 
+2. 分别求出三个红珠子之间的距离 
+3. 对这三段距离从小到大排序 y1, y2, y3
+4. 如果第一段距离y1 小于k，说明需要交换 k - y 次， 同理 第二段距离y2 小于k，说明需要交换 k - y2 次 
+5. y1 y2 都调整好了，不用计算y3，因为 y3是距离最大
+
+```CPP
+#include<bits/stdc++.h>
+using namespace std;
+ 
+int main(){
+    int t;
+    cin >> t;
+    int n, k, a1, a2, a3;
+    vector<int> dis(3);
+
+    while (t--) {
+        cin >> n >> k >> a1 >> a2 >> a3;
+        if(k * 3 > n){
+            cout << -1 << endl;
+            continue;
+        }
+        dis[0] = min(abs(a1 - a2), n - abs(a1 - a2));
+        dis[1] = min(abs(a1 - a3), n - abs(a1 - a3));
+        dis[2] = min(abs(a3 - a2), n - abs(a3 - a2));
+
+        sort(dis.begin(), dis.end());
+
+        int result = 0;
+        if (dis[0] < k) result += (k - dis[0]);
+        if (dis[1] < k) result += (k - dis[1]);
+
+        cout << result << endl;
+    }
+    return 0;
+}
+```
+
+Java代码：
+
+```Java
+import java.util.*;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner scanner = new Scanner(System.in);
+        int t = scanner.nextInt();
+
+        while (t-- > 0) {
+            int n = scanner.nextInt();
+            int k = scanner.nextInt();
+            int a1 = scanner.nextInt();
+            int a2 = scanner.nextInt();
+            int a3 = scanner.nextInt();
+            if (k * 3 > n) {
+                System.out.println(-1);
+                continue;
+            }
+
+            List<Integer> dis = new ArrayList<>(3);
+            dis.add(Math.min(Math.abs(a1 - a2), n - Math.abs(a1 - a2)));
+            dis.add(Math.min(Math.abs(a1 - a3), n - Math.abs(a1 - a3)));
+            dis.add(Math.min(Math.abs(a3 - a2), n - Math.abs(a3 - a2)));
+
+            Collections.sort(dis);
+
+            int result = 0;
+            if (dis.get(0) < k) result += (k - dis.get(0));
+            if (dis.get(1) < k) result += (k - dis.get(1));
+
+            System.out.println(result);
+        }
+    }
+}
+```
--- a/problems/kamacoder/0148.扑克牌同花顺.md
+++ b/problems/kamacoder/0148.扑克牌同花顺.md
@@ -0,0 +1,122 @@
+
+# 扑克牌同花顺 
+
+首先我们要定义一个结构体，来存放我们的数据 
+
+`map<花色，{同一花色牌集合，同一花色的牌对应的牌数量}>`
+
+再遍历 每一个花色下，每一个牌 的数量 
+
+代码如下详细注释：
+
+
+```CPP
+#include<bits/stdc++.h>
+using namespace std;
+
+string cards[] = {"H","S","D","C"};
+typedef long long ll;
+struct color
+{
+    set<int> st; // 同一花色 牌的集合
+    map<int, ll> cnt;  // 同一花色 牌对应的数量
+};
+unordered_map<string, color> umap;
+
+int main() {
+    int n;
+    cin >> n;
+    for (int i = 0; i < n; i++) {
+        int x, y;
+        string card;
+        cin >> x >> y >> card;
+        umap[card].st.insert(x);
+        umap[card].cnt[x] += y;
+    }
+    ll sum = 0;
+    // 遍历每一个花色
+    for (string cardOne : cards) {
+        color colorOne = umap[cardOne];
+        // 遍历 同花色 每一个牌
+        for (int number : colorOne.st) {
+            ll numberCount = colorOne.cnt[number]; // 获取牌为number的数量是 numberCount
+
+            // 统计 number 到 number + 4 都是否有牌，用cal 把 number 到number+4 的数量记下来
+            ll cal = numberCount;
+            for (int j = number + 1; j <= number + 4; j++) cal = min(cal, colorOne.cnt[j]);
+            // 统计结果
+            sum += cal;
+            // 把统计过的同花顺数量减下去
+            for (int j = number + 1; j <= number + 4; j++) colorOne.cnt[j] -= cal;
+        }
+    }
+    cout << sum << endl;
+}
+```
+
+Java代码如下： 
+
+```Java 
+
+import java.util.*;
+
+public class Main {
+    static String[] cards = {"H", "S", "D", "C"}; // 花色数组
+
+    static class Color {
+        Set<Integer> st; // 同一花色牌的集合
+        Map<Integer, Long> cnt;  // 同一花色牌对应的数量
+
+        Color() {
+            st = new HashSet<>(); // 初始化集合
+            cnt = new HashMap<>(); // 初始化映射
+        }
+    }
+
+    static Map<String, Color> umap = new HashMap<>(); // 用于存储每种花色对应的Color对象
+
+    public static void main(String[] args) {
+        Scanner scanner = new Scanner(System.in);
+        int n = scanner.nextInt(); // 读取牌的数量
+
+        for (int i = 0; i < n; i++) {
+            int x = scanner.nextInt(); // 读取牌的值
+            int y = scanner.nextInt(); // 读取牌的数量
+            String card = scanner.next(); // 读取牌的花色
+
+            umap.putIfAbsent(card, new Color()); // 如果不存在该花色，则创建一个新的Color对象
+            umap.get(card).st.add(x); // 将牌的值加入集合
+            umap.get(card).cnt.put(x, umap.get(card).cnt.getOrDefault(x, 0L) + y); // 更新牌的数量
+        }
+
+        long sum = 0; // 结果累加器
+
+        // 遍历每一种花色
+        for (String cardOne : cards) {
+            Color colorOne = umap.getOrDefault(cardOne, new Color()); // 获取对应花色的Color对象
+
+            // 遍历同花色的每一张牌
+            for (int number : colorOne.st) {
+                long numberCount = colorOne.cnt.get(number); // 获取当前牌的数量
+
+                // 计算从当前牌到number+4的最小数量
+                long cal = numberCount;
+                for (int j = number + 1; j <= number + 4; j++) {
+                    cal = Math.min(cal, colorOne.cnt.getOrDefault(j, 0L)); // 更新cal为最小值
+                }
+
+                // 将结果累加到sum
+                sum += cal;
+
+                // 将统计过的同花顺数量减去
+                for (int j = number + 1; j <= number + 4; j++) {
+                    colorOne.cnt.put(j, colorOne.cnt.getOrDefault(j, 0L) - cal);
+                }
+            }
+        }
+
+        System.out.println(sum); // 输出结果
+    }
+}
+ 
+```
--- a/problems/kamacoder/0149.好数组.md
+++ b/problems/kamacoder/0149.好数组.md
@@ -0,0 +1,102 @@
+
+# 149. 好数组
+
+贪心思路：
+
+整体思路是移动到中间位置（中位数），一定是 移动次数最小的。 
+
+有一个数可以不改变，对数组排序之后，  最小数 和 最大数 一定是移动次数最多的，所以分别保留最小 和 最大的不变。
+
+中间可能有两个位置，所以要计算中间偏前 和 中间偏后的
+
+代码如下：
+
+```CPP 
+#include<bits/stdc++.h>
+using namespace std;
+
+int main() {
+    int n;
+    cin >> n;
+    vector<long> arr(n);
+    for (int i = 0; i < n; ++i) {
+        cin >> arr[i];
+    }
+    sort(arr.begin(), arr.end());
+
+    if (arr[0] == arr[n - 1]) {
+        cout << 1 << endl;
+        return 0;
+    }
+    long cnt = 0L;
+    long cnt1 = 0L;
+
+    // 如果要保留一个不改变，要不不改最小的，要不不改最大的。
+
+    // 取中间偏前的位置
+    long mid = arr[(n - 2) / 2];
+
+    // 不改最大的
+    for (int i = 0; i < n - 1; i++) {
+        cnt += abs(arr[i] - mid);
+    }
+
+    // 取中间偏后的位置
+    mid = arr[n / 2];
+
+    // 不改最小的
+    for (int i = 1; i < n; i++) {
+        cnt1 += abs(arr[i] - mid);
+    }
+
+    cout << min(cnt, cnt1) << endl;
+    return 0;
+}
+```
+
+Java代码如下：
+
+```Java 
+
+import java.util.*;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner scanner = new Scanner(System.in);
+        int n = scanner.nextInt();
+        long[] arr = new long[n];
+        for (int i = 0; i < n; ++i) {
+            arr[i] = scanner.nextLong();
+        }
+        Arrays.sort(arr);
+
+        if (arr[0] == arr[n - 1]) {
+            System.out.println(1);
+            return;
+        }
+        long cnt = 0L;
+        long cnt1 = 0L;
+
+        // 如果要保留一个不改变，要不不改最小的，要不不改最大的。
+
+        // 取中间偏前的位置
+        long mid = arr[(n - 2) / 2];
+
+        // 不改最大的
+        for (int i = 0; i < n - 1; i++) {
+            cnt += Math.abs(arr[i] - mid);
+        }
+
+        // 取中间偏后的位置
+        mid = arr[n / 2];
+
+        // 不改最小的
+        for (int i = 1; i < n; i++) {
+            cnt1 += Math.abs(arr[i] - mid);
+        }
+
+        System.out.println(Math.min(cnt, cnt1));
+    }
+}
+
+```
--- a/problems/kamacoder/0150.极长连续段的权值.md
+++ b/problems/kamacoder/0150.极长连续段的权值.md
@@ -0,0 +1,66 @@
+
+# 150. 极长连续段的权值
+
+动态规划，枚举最后边节点的情况： 
+
+```CPP 
+#include <iostream>
+#include <string>
+using namespace std;
+
+int main() {
+    int n;
+    cin >> n;
+    string s;
+    cin >> s;
+
+    long long result = 1;
+    long long a = 1;
+
+    for (int i = 1; i < n; ++i) {
+        // 加上本身长度为1的子串 
+        if (s[i] == s[i - 1]) {
+            a += 1;
+            result += a; 
+        // 以最右节点为终点，每个子串的级长连续段都+1，再加本身长度为1的子串
+        } else {
+            a = a + i + 1;
+            result += a;
+        }
+    }
+    cout << result << endl;
+    return 0;
+} 
+```
+
+Java代码如下：
+
+```Java 
+import java.util.Scanner;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner scanner = new Scanner(System.in);
+        int n = scanner.nextInt();
+        String s = scanner.next();
+
+        long result = 1;
+        long a = 1;
+
+        for (int i = 1; i < n; ++i) {
+            // 加上本身长度为1的子串
+            if (s.charAt(i) == s.charAt(i - 1)) {
+                a += 1;
+                result += a;
+            // 以最右节点为终点，每个子串的级长连续段都+1，再加本身长度为1的子串
+            } else {
+                a = a + i + 1;
+                result += a;
+            }
+        }
+
+        System.out.println(result);
+    }
+}
+ 
+```
--- a/problems/kamacoder/0151.手机流畅运行的秘密.md
+++ b/problems/kamacoder/0151.手机流畅运行的秘密.md
@@ -0,0 +1,127 @@
+# 151. 手机流畅运行的秘密 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1229)
+
+先运行 能留下电量多的 任务，才能有余电运行其他任务。 
+
+任务1，1:10 ，运行完 能留下 9个电
+
+任务2，2:12，运行完 能留下 10个电 
+
+任务3，3:10，运行完 能留下 7个电。 
+
+运行顺序： 任务2 -> 任务1 -> 任务3   
+
+按照  最低初始电量 - 耗电量，从大到小排序。 
+
+计算总电量，需要 从小到大 遍历， 不断取 总电量 +  任务耗电量 与 任务最低初始电量 的最大值。
+
+```CPP
+#include<bits/stdc++.h>
+using namespace std;
+
+bool cmp(const pair<int,int>& taskA, const pair<int,int>& taskB) {
+    return (taskA.second - taskA.first) < (taskB.second - taskB.first);
+}
+int main() {
+    string str, tmp;
+    vector<pair<int,int>> tasks;
+
+    //处理输入
+    getline(cin, str);
+    stringstream ss(str);
+    while (getline(ss, tmp, ',')) {
+        int p = tmp.find(":");
+        string a = tmp.substr(0, p);
+        string b = tmp.substr(p + 1);
+        tasks.push_back({stoi(a), stoi(b)});
+    }
+
+    // 按照差值从小到大排序
+    sort(tasks.begin(), tasks.end(), cmp);
+
+    // 收集结果
+    int result = 0;
+    for (int i = 0 ; i < tasks.size(); i++) {
+        result = max(result + tasks[i].first, tasks[i].second);
+    }
+
+    result =  result <= 4800 ? result : -1;
+    cout << result << endl;
+
+}
+```
+
+Java版本：
+
+```Java 
+import java.util.*;
+import java.util.stream.Collectors;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner sc = new Scanner(System.in);
+        String str = sc.nextLine();
+        String[] tasksArray = str.split(",");
+        List<Pair> tasks = Arrays.stream(tasksArray)
+                                 .map(task -> {
+                                     String[] parts = task.split(":");
+                                     return new Pair(Integer.parseInt(parts[0]), Integer.parseInt(parts[1]));
+                                 })
+                                 .collect(Collectors.toList());
+
+        // 按照差值从小到大排序
+        Collections.sort(tasks, (taskA, taskB) ->
+            (taskA.second - taskA.first) - (taskB.second - taskB.first)
+        );
+
+        // 收集结果
+        int result = 0;
+        for (Pair task : tasks) {
+            result = Math.max(result + task.first, task.second);
+        }
+
+        result = result <= 4800 ? result : -1;
+        System.out.println(result);
+    }
+}
+
+class Pair {
+    int first;
+    int second;
+
+    Pair(int first, int second) {
+        this.first = first;
+        this.second = second;
+    }
+}
+ 
+``` 
+
+Python版本： 
+
+```python 
+def main():
+    import sys
+    input = sys.stdin.read
+
+    str = input().strip()
+    tasks = []
+    for tmp in str.split(','):
+        a, b = map(int, tmp.split(':'))
+        tasks.append((a, b))
+
+    # 按照差值从小到大排序
+    tasks.sort(key=lambda task: task[1] - task[0])
+
+    # 收集结果
+    result = 0
+    for task in tasks:
+        result = max(result + task[0], task[1])
+
+    result = result if result <= 4800 else -1
+    print(result)
+
+if __name__ == "__main__":
+    main()
+```
--- a/problems/kamacoder/0152.小米手机通信校准.md
+++ b/problems/kamacoder/0152.小米手机通信校准.md
@@ -0,0 +1,121 @@
+
+
+# 152. 小米手机通信校准 
+
+[题目链接](https://kamacoder.com/problempage.php?pid=1230)
+
+一道模拟题，但比较考察 代码能力。 
+
+遍历去找 里 freq 最近的 freg就好， 需要记录刚遍历过的的freg和 loss，因为可能有 相邻一样的 freg。
+
+```CPP 
+#include <bits/stdc++.h>
+using namespace std;
+
+int main() {
+    int freq;
+    cin >> freq;
+    string data;
+    double result = 0;
+    int last_freg = 0; // 记录上一个 freg
+    int last_loss = 0; // 记录上一个loss 
+    while(cin >> data) {
+        int index = data.find(':');
+        int freg = stoi(data.substr(0, index)); // 获取 freg 和 loss
+        int loss = stoi(data.substr(index + 1)); 
+        // 两遍一样
+        if(abs(freg - freq) == abs(last_freg - freq))  {
+            result = (double)(last_loss + loss)/2.0;
+        } // 否则更新最新的result
+        else if(abs(freg - freq) < abs(last_freg - freq)){
+            result = (double)loss;
+        }
+        last_freg = freg;
+        last_loss = loss;
+    }
+    printf("%.1lf\n", result);
+    return 0;
+}
+
+```
+
+Java 版本： 
+
+```Java 
+
+import java.util.Scanner;
+
+public class Main {
+    public static void main(String[] args) {
+        Scanner sc = new Scanner(System.in);
+        int freq = sc.nextInt();
+        sc.nextLine(); // 读取换行符
+
+        String inputLine = sc.nextLine(); // 读取包含所有后续输入的行
+        String[] data = inputLine.split(" "); // 根据空格分割输入
+
+        double result = 0;
+        int lastFreq = 0; // 记录上一个 freg
+        int lastLoss = 0; // 记录上一个 loss
+
+        for (String entry : data) {
+            int index = entry.indexOf(':');
+            int freg = Integer.parseInt(entry.substring(0, index)); // 获取 freg 和 loss
+            int loss = Integer.parseInt(entry.substring(index + 1));
+
+            // 两遍一样
+            if (Math.abs(freg - freq) == Math.abs(lastFreq - freq)) {
+                result = (double) (lastLoss + loss) / 2.0;
+            }
+            // 否则更新最新的 result
+            else if (Math.abs(freg - freq) < Math.abs(lastFreq - freq)) {
+                result = (double) loss;
+            }
+
+            lastFreq = freg;
+            lastLoss = loss;
+        }
+
+        System.out.printf("%.1f\n", result);
+        sc.close();
+    }
+}
+
+```
+
+Python版本： 
+
+```python 
+def main():
+    import sys
+    input = sys.stdin.read
+    data = input().split()
+
+    freq = int(data[0])
+    result = 0
+    last_freg = 0  # 记录上一个 freg
+    last_loss = 0  # 记录上一个 loss
+
+    for i in range(1, len(data)):
+        item = data[i]
+        index = item.find(':')
+        freg = int(item[:index])  # 获取 freg 和 loss
+        loss = int(item[index + 1:])
+
+        # 两遍一样
+        if abs(freg - freq) == abs(last_freg - freq):
+            result = (last_loss + loss) / 2.0
+        # 否则更新最新的 result
+        elif abs(freg - freq) < abs(last_freg - freq):
+            result = loss
+
+        last_freg = freg
+        last_loss = loss
+
+    print(f"{result:.1f}")
+
+if __name__ == "__main__":
+    main()
+
+
+```
--- a/problems/kamacoder/两个字符串的最小ASCII删除总和.md
+++ b/problems/kamacoder/两个字符串的最小ASCII删除总和.md
@@ -1,30 +0,0 @@
-
-
-本题和[代码随想录：两个字符串的删除操作](https://www.programmercarl.com/0583.%E4%B8%A4%E4%B8%AA%E5%AD%97%E7%AC%A6%E4%B8%B2%E7%9A%84%E5%88%A0%E9%99%A4%E6%93%8D%E4%BD%9C.html) 思路基本是一样的。 
-
-
-```CPP 
-#include <iostream>
-#include <vector>
-using namespace std;
-int main() {
-    string s1, s2;
-    cin >> s1 >> s2;
-    vector<vector<int>> dp(s1.size() + 1, vector<int>(s2.size() + 1, 0));
-
-    // s1 如果变成空串的最小删除ASCLL值综合
-    for (int i = 1; i <= s1.size(); i++) dp[i][0] = dp[i - 1][0] + s1[i - 1];
-    // s2 如果变成空串的最小删除ASCLL值综合
-    for (int j = 1; j <= s2.size(); j++) dp[0][j] = dp[0][j - 1] + s2[j - 1];
-
-    for (int i = 1; i <= s1.size(); i++) {
-        for (int j = 1; j <= s2.size(); j++) {
-            if (s1[i - 1] == s2[j - 1]) dp[i][j] = dp[i - 1][j - 1];
-            else dp[i][j] = min(dp[i - 1][j] + s1[i - 1], dp[i][j - 1] + s2[j - 1]);
-        }
-    }
-    cout << dp[s1.size()][s2.size()] << endl;
-
-}
-```
-
--- a/problems/kamacoder/小红的区间翻转.md
+++ b/problems/kamacoder/小红的区间翻转.md
@@ -1,109 +0,0 @@
-
-
-
-import java.util.Scanner;
-
-public class Main {
-
-    public static void main(String[] args) {
-        Scanner sc = new Scanner(System.in);
-        int n = sc.nextInt();
-        int[] a = new int[n];
-        int[] b = new int[n];
-
-        for (int i = 0; i < n; i++) {
-            a[i] = sc.nextInt();
-        }
-
-        for (int i = 0; i < n; i++) {
-            b[i] = sc.nextInt();
-        }
-
-        int  p = -1, s = -1;
-        for (int i = 0; i < n; i++) {
-            if (a[i] == b[i]) p = i;
-            else break;
-        }
-
-        for (int j = n - 1 ; j >= 0 ; j--) {
-            if (a[j] == b[j]) s = j;
-            else break;
-        }
-
-
-        boolean[][] dp = new boolean[n][n];
-        int res = 0;
-
-        for (int j = 0; j < n; j++) {
-            for (int i = j ; i >= 0 ; i--) {
-                if (i == j) dp[i][j] = a[i] == b[i];
-                else if (i + 1 == j) dp[i][j] = (a[i] == b[j] && a[j] == b[i]);
-                else {
-                    dp[i][j] = dp[i+1][j-1] && (a[i] == b[j] && a[j] == b[i]);
-                }
-                if (dp[i][j] && (i == 0 || p >= i-1) && (j == n - 1 || j+1 >= s))  res++;
-            }
-        }
-        System.out.println(res);
-    }
-
-}
-
-
-import java.util.Scanner;
-
-public class Main {
-    public static void main(String[] args) {
-        Scanner sc = new Scanner(System.in);
-        int n = sc.nextInt();
-
-        int[] a = new int[n];
-        int[] b = new int[n];
-
-        for (int i = 0; i < n; i++) {
-            a[i] = sc.nextInt();
-        }
-
-        for (int i = 0; i < n; i++) {
-            b[i] = sc.nextInt();
-        }
-
-        int count = 0;
-
-        // 遍历所有可能的区间
-        for (int left = 0; left < n; left++) {
-            for (int right = left; right < n; right++) {
-                // 检查翻转区间 [left, right] 后，a 是否可以变成 b
-                if (canTransform(a, b, left, right)) {
-                    count++;
-                }
-            }
-        }
-
-        System.out.println(count);
-    }
-
-    private static boolean canTransform(int[] a, int[] b, int left, int right) {
-        // 提前检查翻转区间的值是否可以匹配
-        for (int i = left, j = right; i <= right; i++, j--) {
-            if (a[i] != b[j]) {
-                return false;
-            }
-        }
-
-        // 检查翻转区间外的值是否匹配
-        for (int i = 0; i < left; i++) {
-            if (a[i] != b[i]) {
-                return false;
-            }
-        }
-
-        for (int i = right + 1; i < a.length; i++) {
-            if (a[i] != b[i]) {
-                return false;
-            }
-        }
-
-        return true;
-    }
-}
--- a/problems/kamacoder/最长同值路径.md
+++ b/problems/kamacoder/最长同值路径.md
@@ -1,81 +0,0 @@
-
-
-
-
-```CPP
-#include <iostream>
-#include <queue>
-#include <vector>
-
-using namespace std;
-
-// 定义二叉树节点结构
-struct TreeNode {
-    int val;
-    TreeNode* left;
-    TreeNode* right;
-    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
-};
-
-// 根据层序遍历数组构建二叉树
-TreeNode* constructBinaryTree(const vector<string>& levelOrder) {
-    if (levelOrder.empty()) return NULL;
-
-    TreeNode* root = new TreeNode(stoi(levelOrder[0]));
-    queue<TreeNode*> q;
-    q.push(root);
-    int i = 1;
-
-    while (!q.empty() && i < levelOrder.size()) {
-        TreeNode* current = q.front();
-        q.pop();
-
-        if (i < levelOrder.size() && levelOrder[i] != "null") {
-            current->left = new TreeNode(stoi(levelOrder[i]));
-            q.push(current->left);
-        }
-        i++;
-
-        if (i < levelOrder.size() && levelOrder[i] != "null") {
-            current->right = new TreeNode(stoi(levelOrder[i]));
-            q.push(current->right);
-        }
-        i++;
-    }
-
-    return root;
-}
-
-int result = 0;
-int dfs(TreeNode* node) {
-    if (node == NULL) return 0;
-    int leftPath = dfs(node->left);
-    int rightPath = dfs(node->right);
-
-    int leftNum = 0, rightNum = 0;
-    if (node->left != NULL && node->left->val == node->val) {
-        leftNum = leftPath + 1;
-    }
-    if (node->right != NULL && node->right->val == node->val) {
-        rightNum = rightPath + 1;
-    }
-    result = max(result, leftNum + rightNum);
-    return max(leftNum, rightNum);
-
-}
-
-
-int main() {
-    int n;
-    cin >> n;
-    vector<string> levelOrder(n);
-    for (int i = 0; i < n ; i++) cin >> levelOrder[i];
-
-    TreeNode* root = constructBinaryTree(levelOrder);
-    dfs(root);
-    cout << result << endl;
-
-    return 0;
-}
-```
-