Update

problems/0222.完全二叉树的节点个数.md

@@ -34,7 +34,6 @@
 
 本篇给出按照普通二叉树的求法以及利用完全二叉树性质的求法。
 
-
 ## 普通二叉树
 
 首先按照普通二叉树的逻辑来求。
@@ -145,6 +144,14 @@ public:
 
 以上方法都是按照普通二叉树来做的，对于完全二叉树特性不了解的同学可以看这篇 [关于二叉树，你该了解这些！](https://programmercarl.com/二叉树理论基础.html)，这篇详细介绍了各种二叉树的特性。
 
+在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2^(h-1)  个节点。
+
+**大家要自己看完全二叉树的定义，很多同学对完全二叉树其实不是真正的懂了。**
+
+我来举一个典型的例子如题：
+
+<img src='https://img-blog.csdnimg.cn/20200920221638903.png' width=600> </img></div>
+
 完全二叉树只有两种情况，情况一：就是满二叉树，情况二：最后一层叶子节点没有满。
 
 对于情况一，可以直接用 2^树深度 - 1 来计算，注意这里根节点深度为1。
@@ -159,7 +166,59 @@ public:
 
 可以看出如果整个树不是满二叉树，就递归其左右孩子，直到遇到满二叉树为止，用公式计算这个子树（满二叉树）的节点数量。
 
-C++代码如下：
+这里关键在于如果去判断一个左子树或者右子树是不是满二叉树呢？ 
+
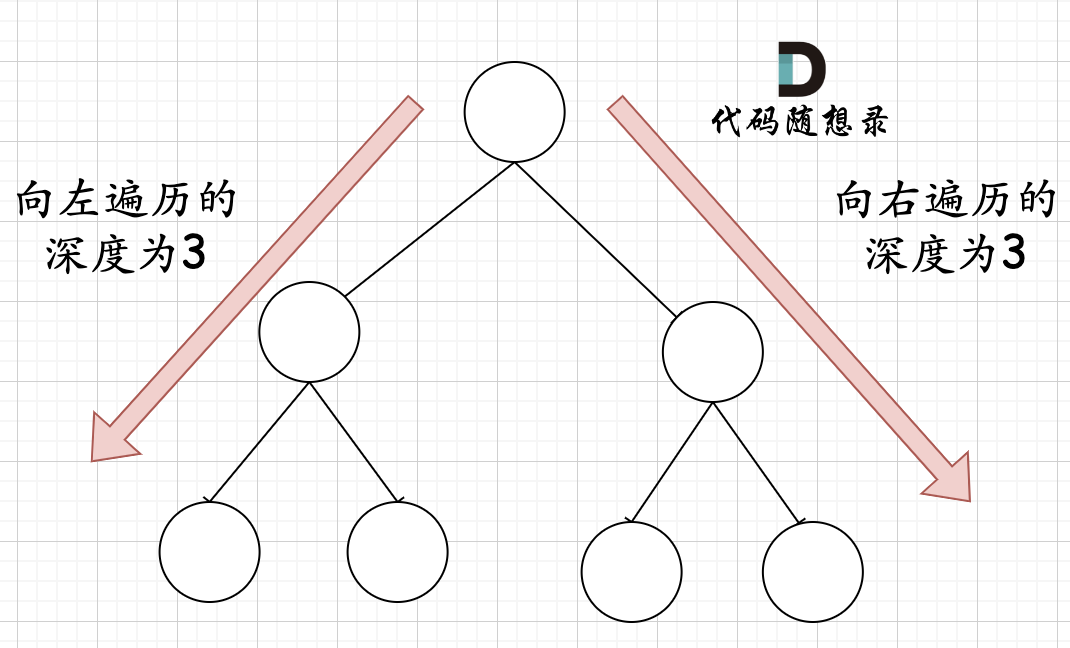
+在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树。如图： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163554.png) 
+
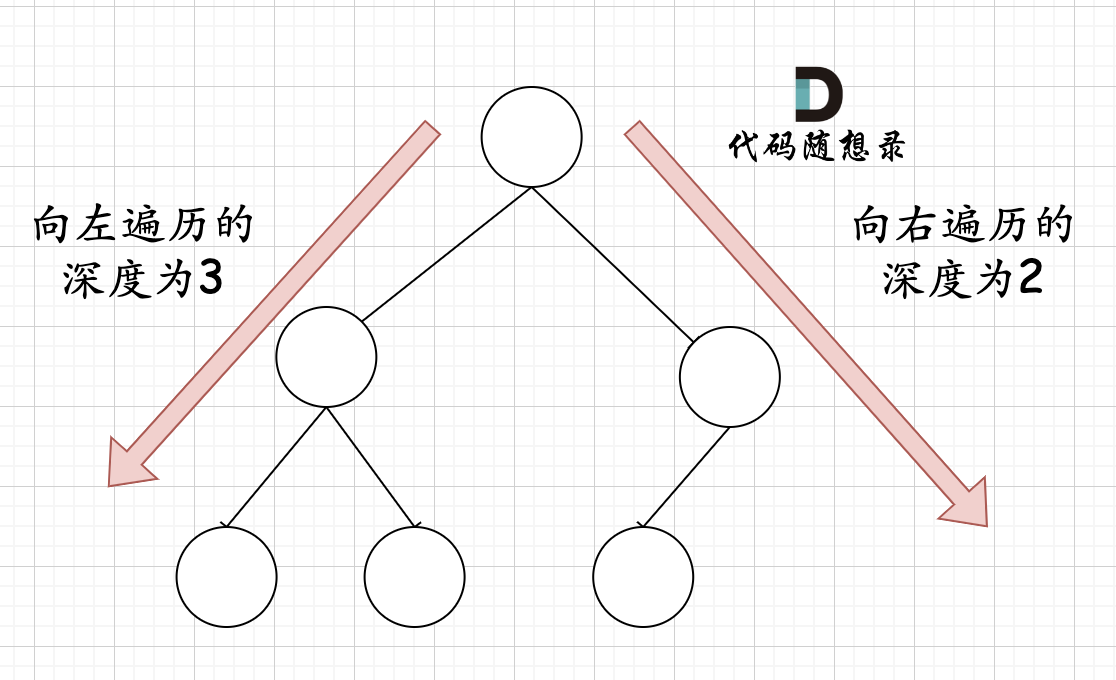
+在完全二叉树中，如果递归向左遍历的深度不等于递归向右遍历的深度，则说明不是满二叉树，如图：  
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163709.png) 
+
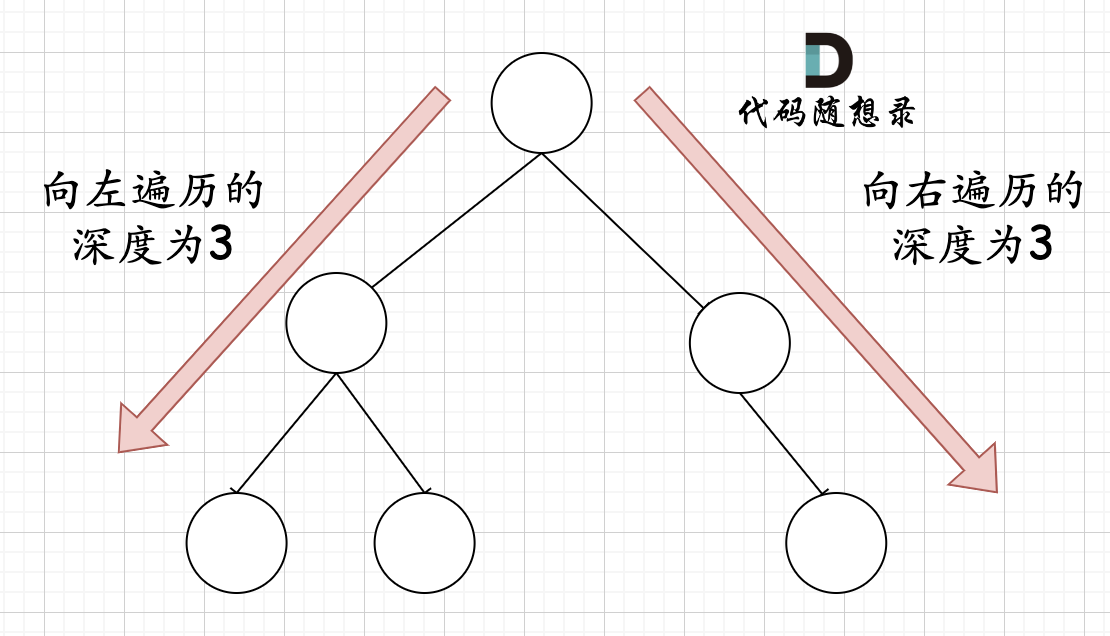
+哪有录友说了，这种情况，递归向左遍历的深度等于递归向右遍历的深度，但也不是满二叉树，如题： 
+
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220829163811.png) 
+
+如果这么想，大家就是对 完全二叉树理解有误区了，**以上这棵二叉树，它根本就不是一个完全二叉树**！ 
+
+判断其子树岂不是满二叉树，如果是则利用用公式计算这个子树（满二叉树）的节点数量，如果不是则继续递归，那么 在递归三部曲中，第二部：终止条件的写法应该是这样的： 
+
+```CPP
+if (root == nullptr) return 0; 
+// 开始根据做深度和有深度是否相同来判断该子树是不是满二叉树
+TreeNode* left = root->left;
+TreeNode* right = root->right;
+int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
+while (left) {  // 求左子树深度
+    left = left->left;
+    leftDepth++;
+}
+while (right) { // 求右子树深度
+    right = right->right;
+    rightDepth++;
+}
+if (leftDepth == rightDepth) {
+    return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，返回满足满二叉树的子树节点数量
+}
+```
+
+递归三部曲，第三部，单层递归的逻辑：（可以看出使用后序遍历）
+
+```CPP 
+int leftTreeNum = countNodes(root->left);       // 左
+int rightTreeNum = countNodes(root->right);     // 右
+int result = leftTreeNum + rightTreeNum + 1;    // 中
+return result;
+```
+
+该部分精简之后代码为：  
+
+```CPP 
+return countNodes(root->left) + countNodes(root->right) + 1; 
+```
+
+最后整体C++代码如下：
 
 ```CPP
 class Solution {
@@ -168,17 +227,17 @@ public:
         if (root == nullptr) return 0;
         TreeNode* left = root->left;
         TreeNode* right = root->right;
-        int leftHeight = 0, rightHeight = 0; // 这里初始为0是有目的的，为了下面求指数方便
+        int leftDepth = 0, rightDepth = 0; // 这里初始为0是有目的的，为了下面求指数方便
         while (left) {  // 求左子树深度
             left = left->left;
-            leftHeight++;
+            leftDepth++;
         }
         while (right) { // 求右子树深度
             right = right->right;
-            rightHeight++;
+            rightDepth++;
         }
-        if (leftHeight == rightHeight) {
-            return (2 << leftHeight) - 1; // 注意(2<<1) 相当于2^2，所以leftHeight初始为0
+        if (leftDepth == rightDepth) {
+            return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，所以leftDepth初始为0
         }
         return countNodes(root->left) + countNodes(root->right) + 1;
     }
@@ -310,16 +369,16 @@ class Solution:
             return 0
         left = root.left
         right = root.right
-        leftHeight = 0 #这里初始为0是有目的的，为了下面求指数方便
-        rightHeight = 0
+        leftDepth = 0 #这里初始为0是有目的的，为了下面求指数方便
+        rightDepth = 0
         while left: #求左子树深度
             left = left.left
-            leftHeight += 1
+            leftDepth += 1
         while right: #求右子树深度
             right = right.right
-            rightHeight += 1
-        if leftHeight == rightHeight:
-            return (2 << leftHeight) - 1 #注意(2<<1) 相当于2^2，所以leftHeight初始为0
+            rightDepth += 1
+        if leftDepth == rightDepth:
+            return (2 << leftDepth) - 1 #注意(2<<1) 相当于2^2，所以leftDepth初始为0
         return self.countNodes(root.left) + self.countNodes(root.right) + 1
 ```
 
@@ -431,17 +490,17 @@ var countNodes = function(root) {
     }
     let left=root.left;
     let right=root.right;
-    let leftHeight=0,rightHeight=0;
+    let leftDepth=0,rightDepth=0;
     while(left){
         left=left.left;
-        leftHeight++;
+        leftDepth++;
     }
     while(right){
         right=right.right;
-        rightHeight++;
+        rightDepth++;
     }
-    if(leftHeight==rightHeight){
-        return Math.pow(2,leftHeight+1)-1;
+    if(leftDepth==rightDepth){
+        return Math.pow(2,leftDepth+1)-1;
     }
     return countNodes(root.left)+countNodes(root.right)+1;
 };
@@ -554,24 +613,24 @@ int countNodes(struct TreeNode* root){
 int countNodes(struct TreeNode* root){
     if(!root)
         return 0;
-    int leftHeight = 0;
-    int rightHeight = 0;
+    int leftDepth = 0;
+    int rightDepth = 0;
     struct TreeNode* rightNode = root->right;
     struct TreeNode* leftNode = root->left;
     //求出左子树深度
     while(leftNode) {
         leftNode = leftNode->left;
-        leftHeight++;
+        leftDepth++;
     }
 
     //求出右子树深度
     while(rightNode) {
         rightNode = rightNode->right;
-        rightHeight++;
+        rightDepth++;
     }
     //若左右子树深度相同，为满二叉树。结点个数为2^height-1
-    if(rightHeight == leftHeight) {
-        return (2 << leftHeight) - 1;
+    if(rightDepth == leftDepth) {
+        return (2 << leftDepth) - 1;
     }
     //否则返回左右子树的结点个数+1
     return countNodes(root->right) + countNodes(root->left) + 1;