CS_learn/leetcode-master
1
0
Fork 0
mirror of https://github.com/youngyangyang04/leetcode-master.git synced 2026-02-02 18:39:09 +08:00
Code Issues Packages Projects Releases Wiki Activity

更新图片链接

Browse Source
This commit is contained in:
kama
2025-05-19 17:11:04 +08:00
parent b489cb69b5
commit ce6e658d14
315 changed files with 2499 additions and 1729 deletions
Download Patch File Download Diff File Expand all files Collapse all files

8
problems/前序/递归算法的时间与空间复杂度分析.md
View File

@@ -29,7 +29,7 @@ int fibonacci(int i) {
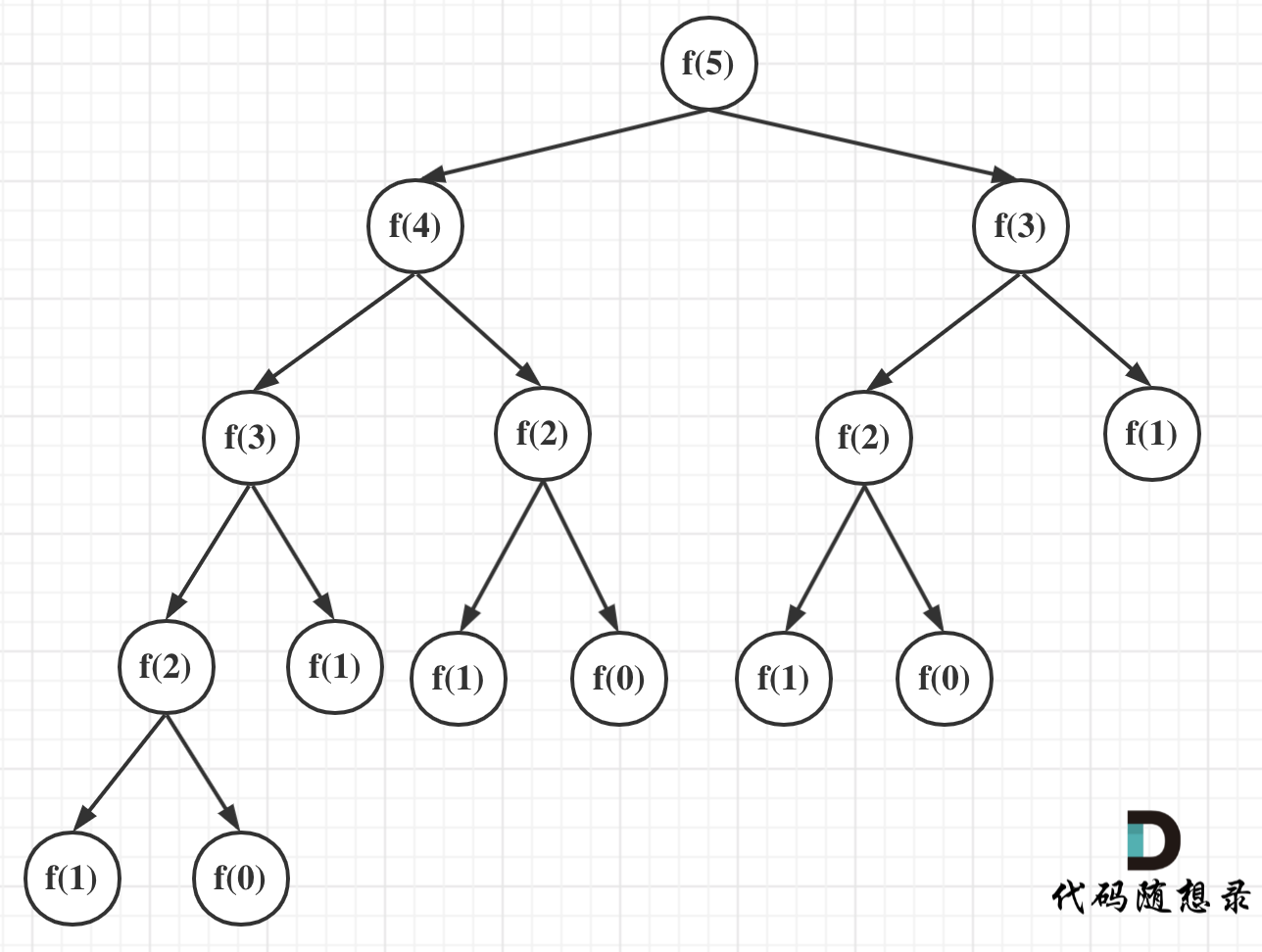
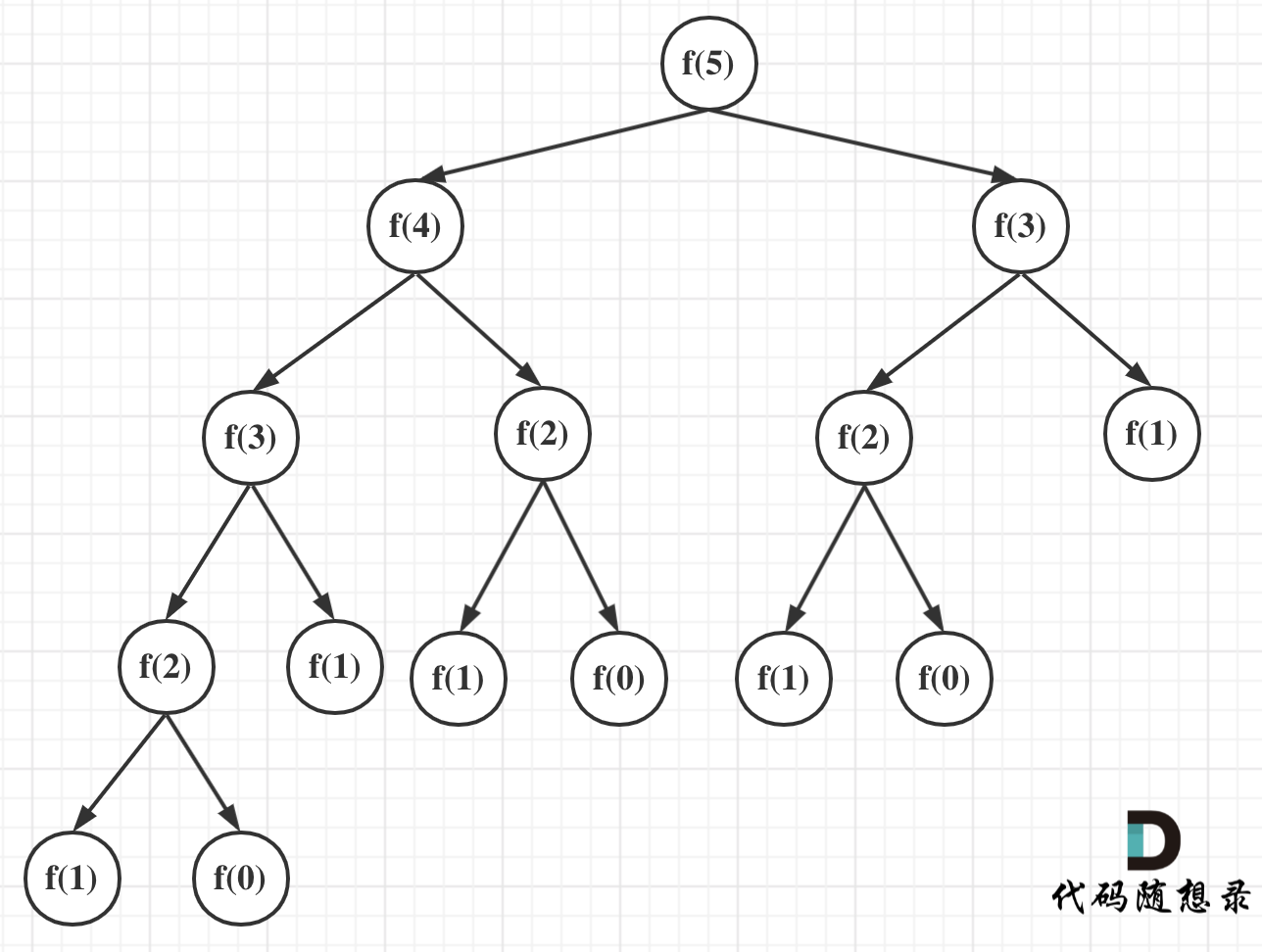
可以看出上面的代码每次递归都是O(1)的操作。再来看递归了多少次，这里将i为5作为输入的递归过程 抽象成一棵递归树，如图：
![递归空间复杂度分析](https://file.kamacoder.com/pics/20210305093200104.png)
![递归空间复杂度分析](https://file1.kamacoder.com/i/algo/20210305093200104.png)
从图中，可以看出f(5)是由f(4)和f(3)相加而来，那么f(4)是由f(3)和f(2)相加而来 以此类推。
@@ -196,7 +196,7 @@ int main()
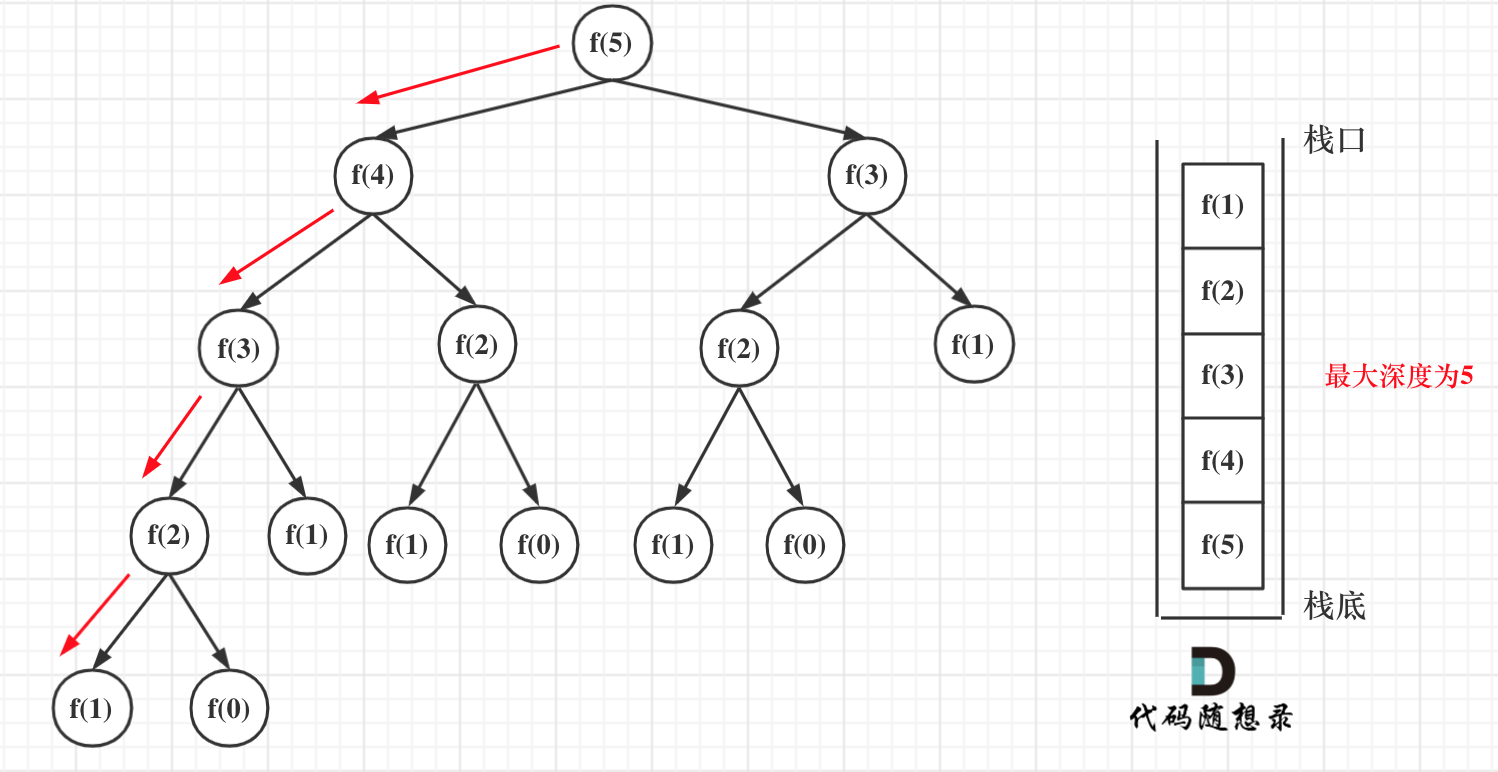
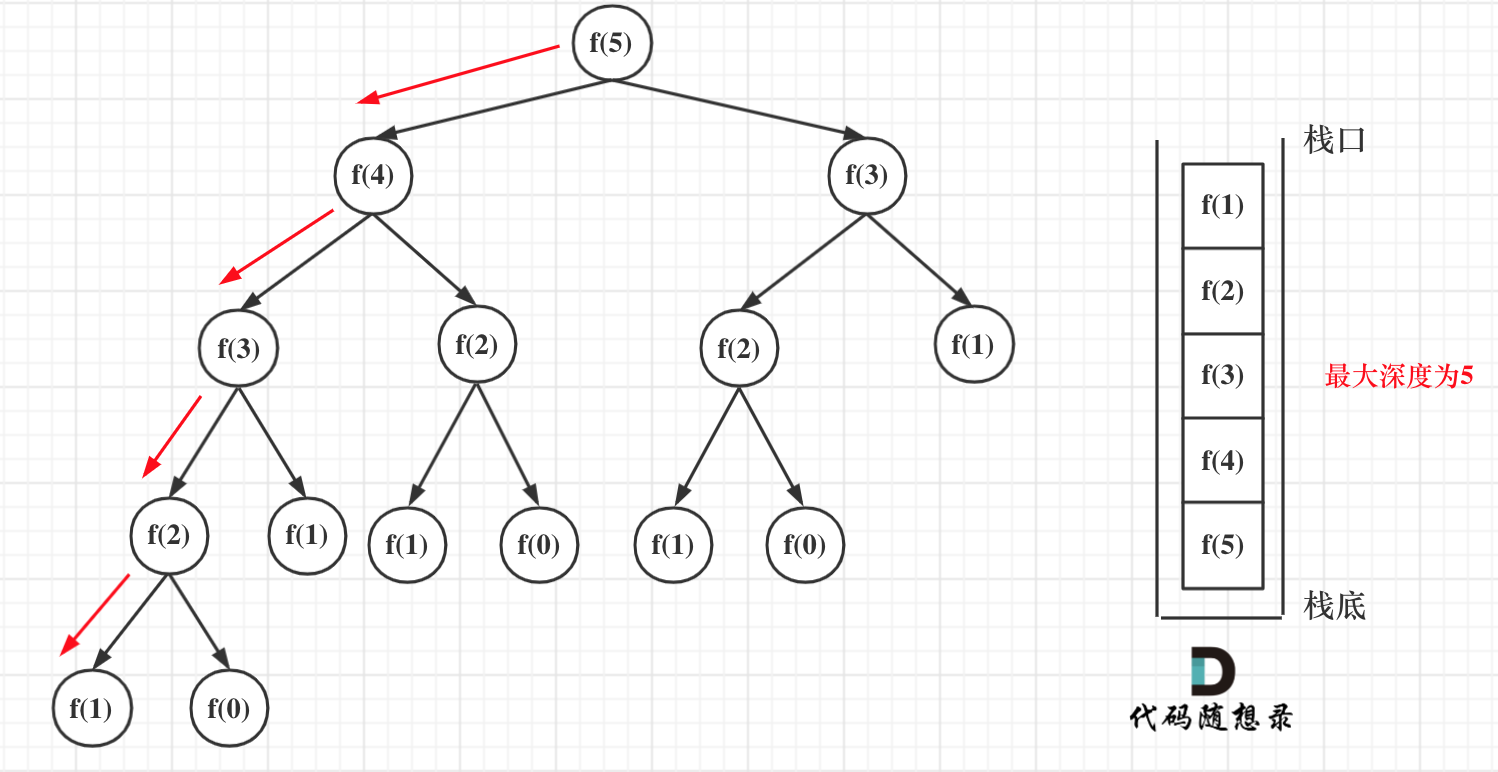
在看递归的深度是多少呢？如图所示：
![递归空间复杂度分析](https://file.kamacoder.com/pics/20210305094749554.png)
![递归空间复杂度分析](https://file1.kamacoder.com/i/algo/20210305094749554.png)
递归第n个斐波那契数的话，递归调用栈的深度就是n。
@@ -214,7 +214,7 @@ int fibonacci(int i) {
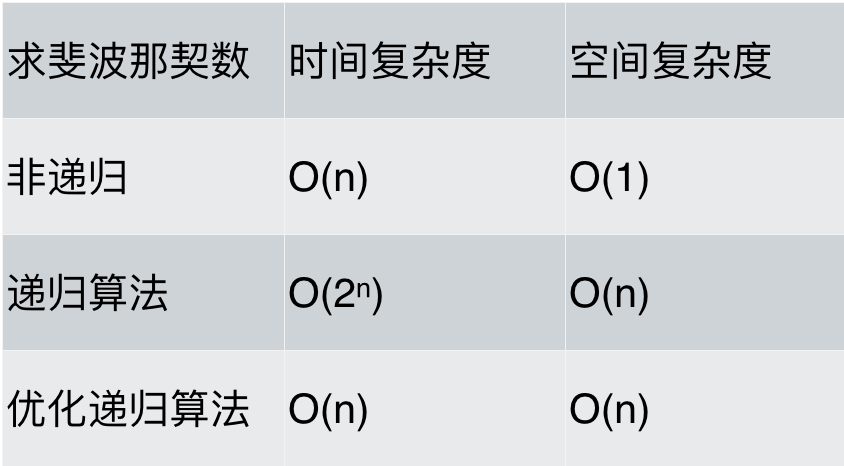
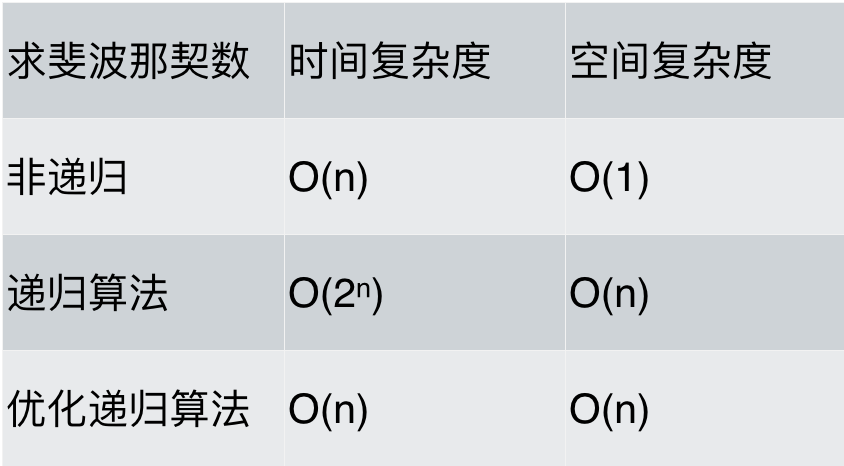
最后对各种求斐波那契数列方法的性能做一下分析，如题：
![递归的空间复杂度分析](https://file.kamacoder.com/pics/20210305095227356.png)
![递归的空间复杂度分析](https://file1.kamacoder.com/i/algo/20210305095227356.png)
可以看出，求斐波那契数的时候，使用递归算法并不一定是在性能上是最优的，但递归确实简化的代码层面的复杂度。
@@ -264,4 +264,4 @@ int binary_search( int arr[], int l, int r, int x) {
-----------------------
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码.jpg width=450> </img></div>
<div align="center"><img src='https://file1.kamacoder.com/i/algo/01二维码.jpg' width=450> </img></div>