更新图片链接

problems/0236.二叉树的最近公共祖先.md

@@ -16,7 +16,7 @@
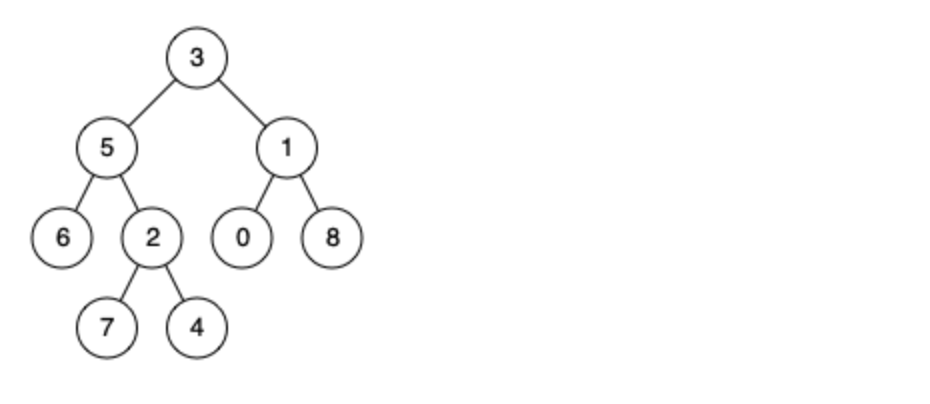
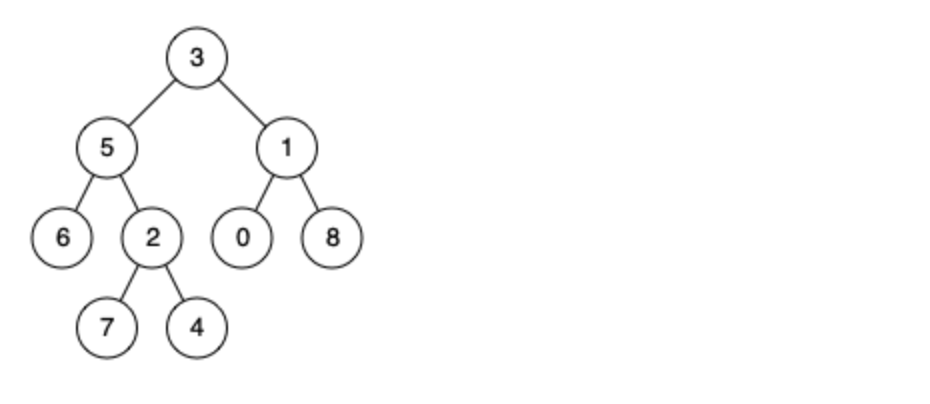
 例如，给定如下二叉树:  root = [3,5,1,6,2,0,8,null,null,7,4]
 
 
-![236. 二叉树的最近公共祖先](https://file.kamacoder.com/pics/20201016173414722.png)
+![236. 二叉树的最近公共祖先](https://file1.kamacoder.com/i/algo/20201016173414722.png)
 
 示例 1:
 输入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
@@ -51,7 +51,7 @@
 
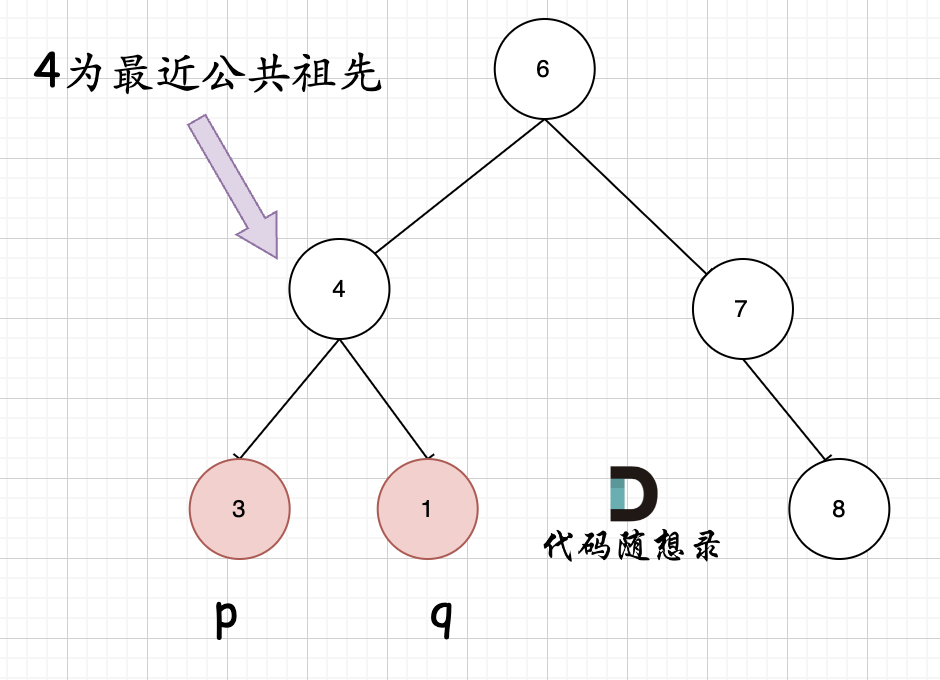
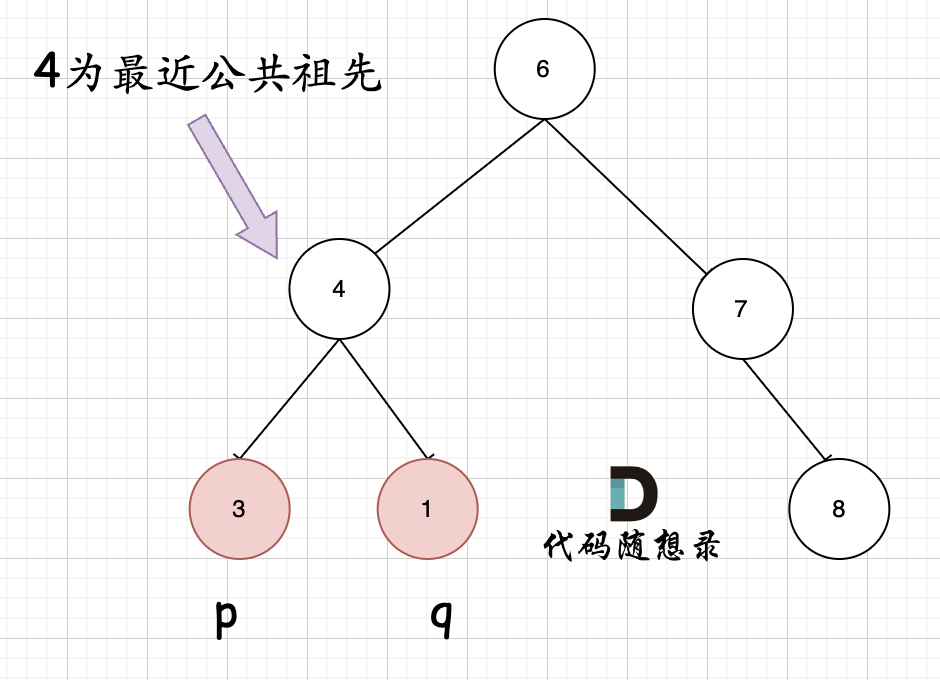
 **首先最容易想到的一个情况：如果找到一个节点，发现左子树出现结点p，右子树出现节点q，或者 左子树出现结点q，右子树出现节点p，那么该节点就是节点p和q的最近公共祖先。** 即情况一： 
 
-![](https://file.kamacoder.com/pics/20220922173502.png)
+![](https://file1.kamacoder.com/i/algo/20220922173502.png)
 
 判断逻辑是 如果递归遍历遇到q，就将q返回，遇到p 就将p返回，那么如果 左右子树的返回值都不为空，说明此时的中节点，一定是q 和p 的最近祖先。 
 
@@ -61,7 +61,7 @@
 
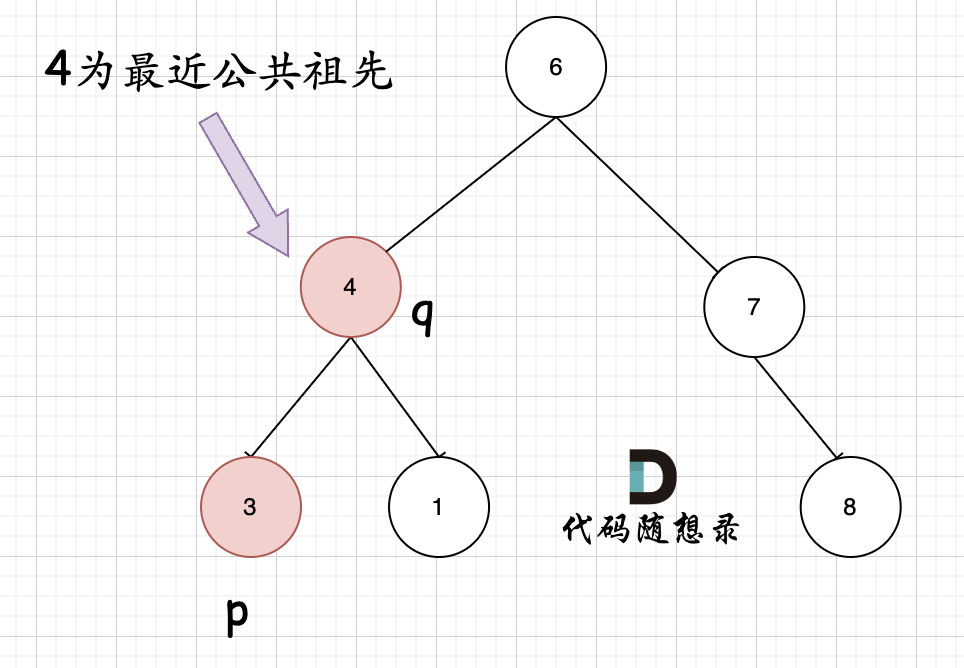
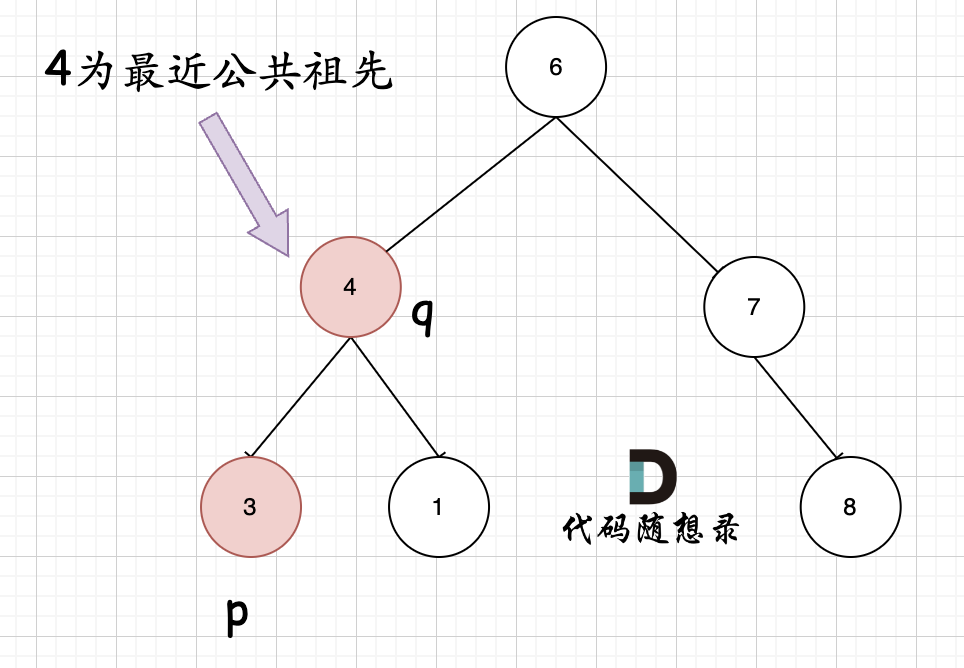
 **但是很多人容易忽略一个情况，就是节点本身p(q)，它拥有一个子孙节点q(p)。** 情况二： 
 
-![](https://file.kamacoder.com/pics/20220922173530.png)
+![](https://file1.kamacoder.com/i/algo/20220922173530.png)
 
 其实情况一 和 情况二 代码实现过程都是一样的，也可以说，实现情况一的逻辑，顺便包含了情况二。 
 
@@ -129,7 +129,7 @@ left与right的逻辑处理;         // 中
 
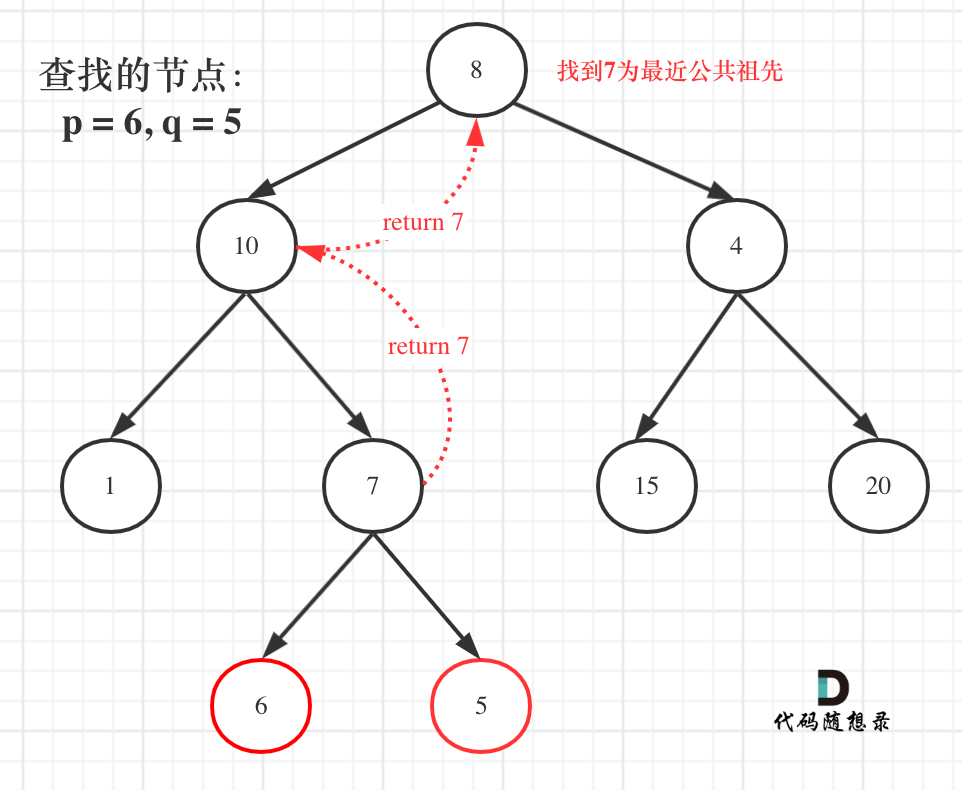
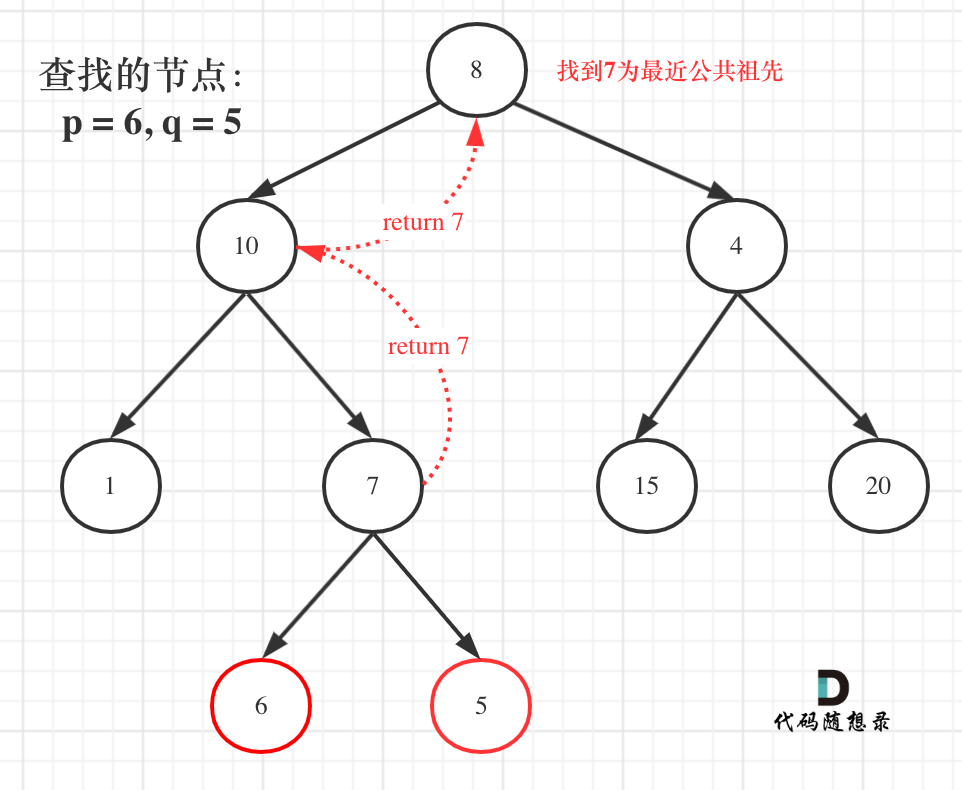
 如图：
 
-![236.二叉树的最近公共祖先](https://file.kamacoder.com/pics/2021020415105872.png)
+![236.二叉树的最近公共祖先](https://file1.kamacoder.com/i/algo/2021020415105872.png)
 
 就像图中一样直接返回7。
 
@@ -162,7 +162,7 @@ TreeNode* right = lowestCommonAncestor(root->right, p, q);
 
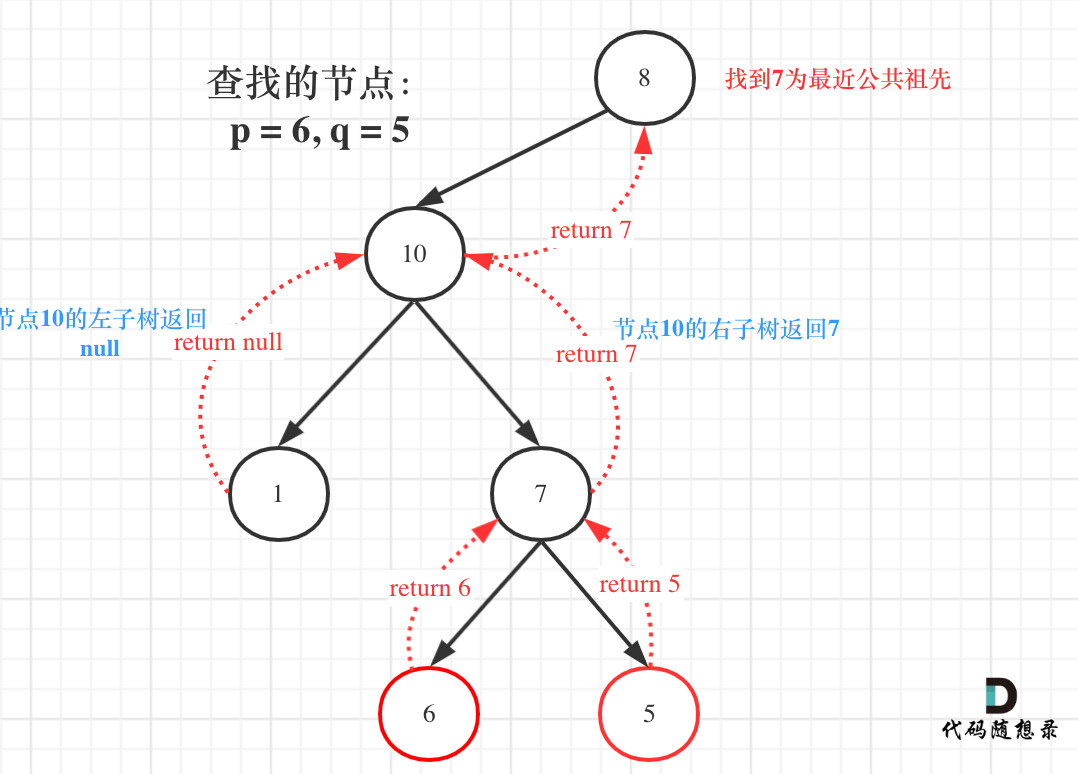
 如图：
 
-![236.二叉树的最近公共祖先1](https://file.kamacoder.com/pics/20210204151125844.png)
+![236.二叉树的最近公共祖先1](https://file1.kamacoder.com/i/algo/20210204151125844.png)
 
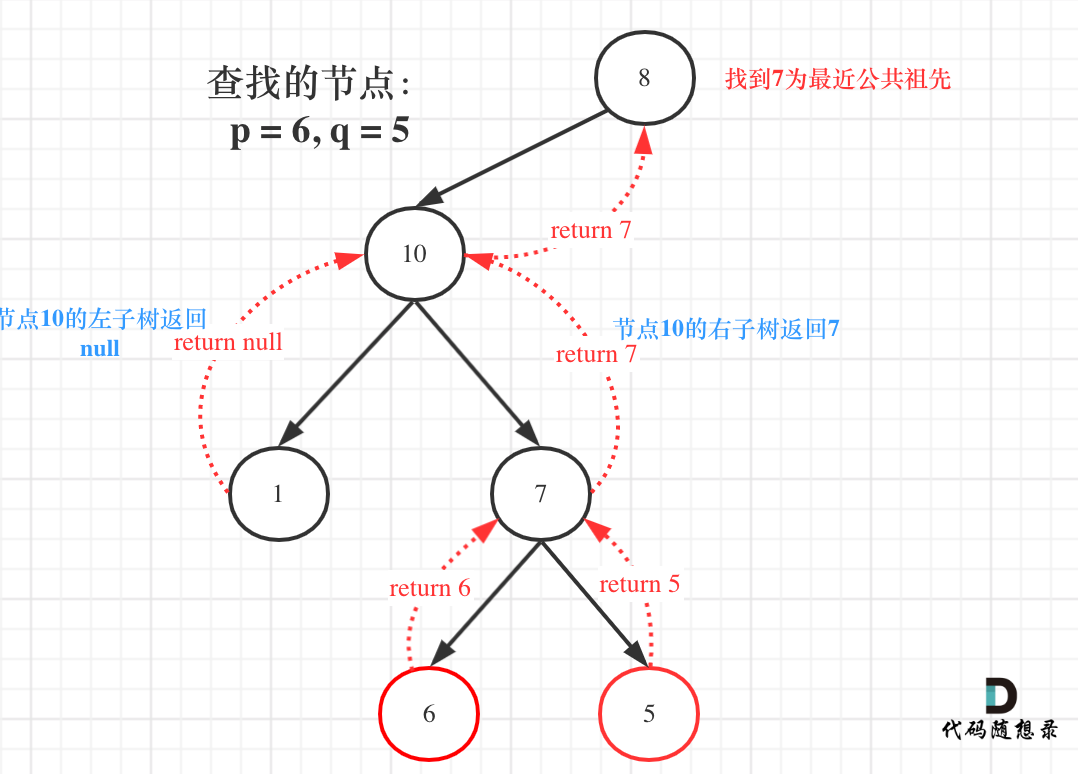
 图中节点10的左子树返回null，右子树返回目标值7，那么此时节点10的处理逻辑就是把右子树的返回值（最近公共祖先7）返回上去！
 
@@ -183,7 +183,7 @@ else  { //  (left == NULL && right == NULL)
 
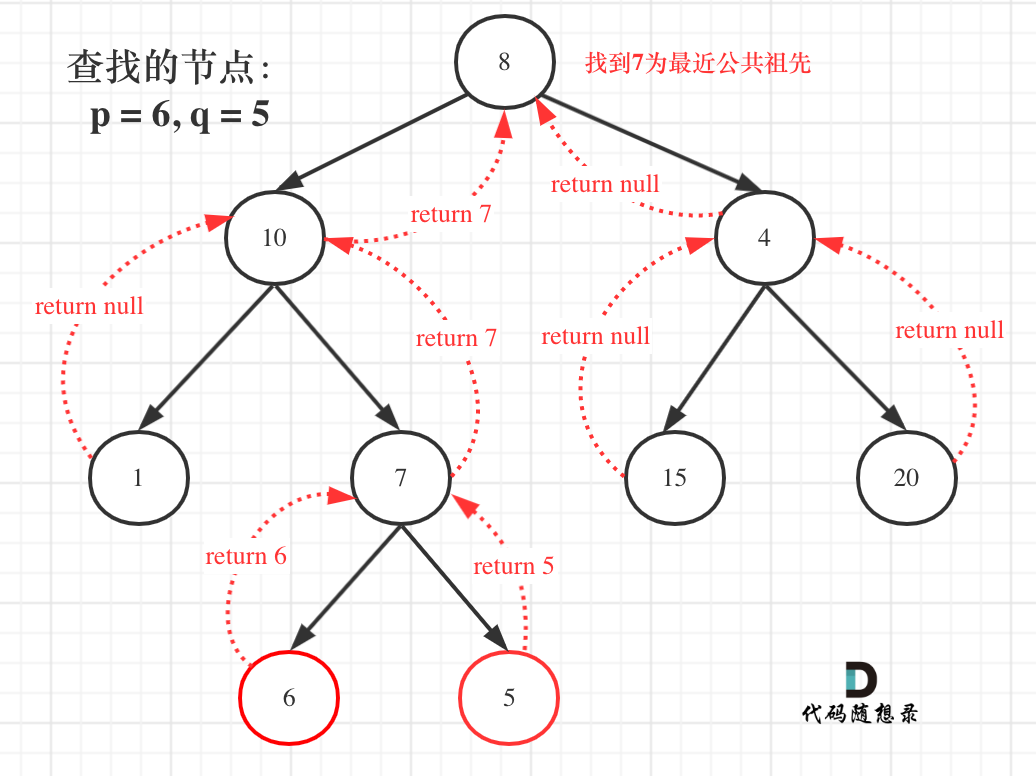
 那么寻找最小公共祖先，完整流程图如下：
 
-![236.二叉树的最近公共祖先2](https://file.kamacoder.com/pics/202102041512582.png)
+![236.二叉树的最近公共祖先2](https://file1.kamacoder.com/i/algo/202102041512582.png)
 
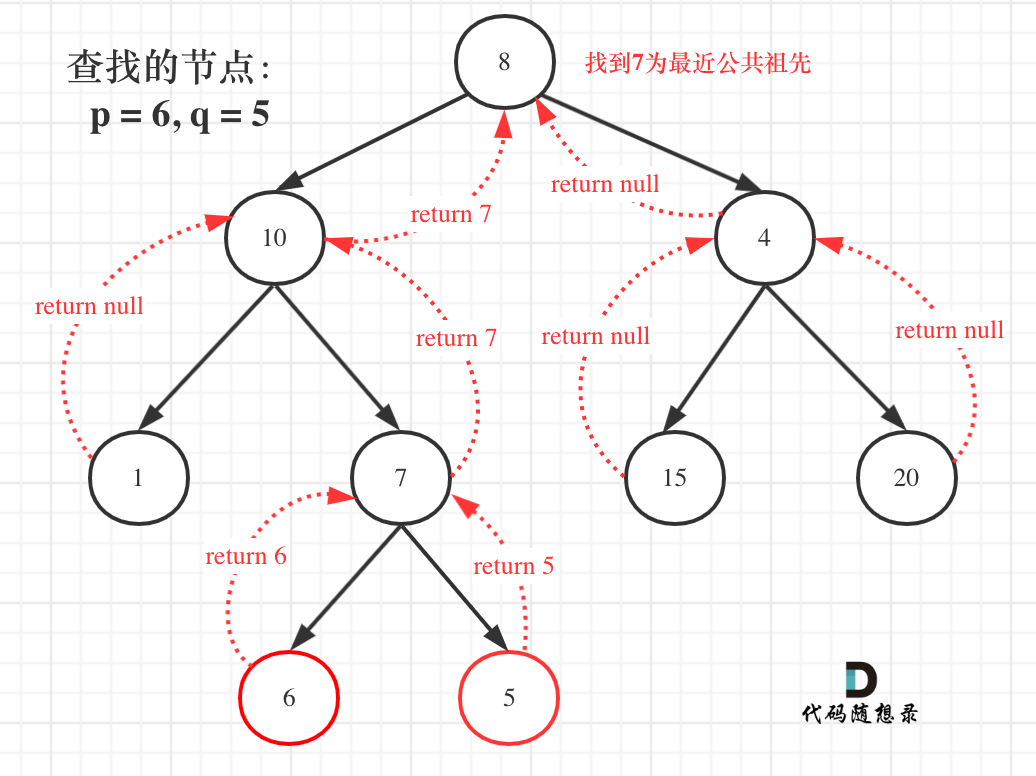
 **从图中，大家可以看到，我们是如何回溯遍历整棵二叉树，将结果返回给头结点的！**