Update

problems/kamacoder/0044.开发商购买土地.md

@@ -388,6 +388,62 @@ if __name__ == "__main__":
     main()
 
 ```
+
+### JavaScript
+
+前缀和
+```js
+function func() {
+    const readline = require('readline')
+    const rl = readline.createInterface({
+        input: process.stdin,
+        output: process.stdout
+    })
+    let inputLines = []
+    rl.on('line', function (line) {
+        inputLines.push(line.trim())
+    })
+
+    rl.on('close', function () {
+        let [n, m] = inputLines[0].split(" ").map(Number)
+        let c = new Array(n).fill(0)
+        let r = new Array(m).fill(0)
+        let arr = new Array(n)
+        let sum = 0//数组总和
+        let min = Infinity//设置最小值的初始值为无限大
+        //定义数组
+        for (let s = 0; s < n; s++) {
+            arr[s] = inputLines[s + 1].split(" ").map(Number)
+        }
+        //每一行的和
+        for (let i = 0; i < n; i++) {
+            for (let j = 0; j < m; j++) {
+                c[i] += arr[i][j]
+                sum += arr[i][j]
+            }
+        }
+        //每一列的和
+        for (let i = 0; i < n; i++) {
+            for (let j = 0; j < m; j++) {
+                r[j] += arr[i][j]
+            }
+        }
+        let sum1 = 0, sum2 = 0
+        //横向切割
+        for (let i = 0; i < n; i++) {
+            sum1 += c[i]
+            min = min < Math.abs(sum - 2 * sum1) ? min : Math.abs(sum - 2 * sum1)
+        }
+        //纵向切割
+        for (let j = 0; j < m; j++) {
+            sum2 += r[j]
+            min = min < Math.abs(sum - 2 * sum2) ? min : Math.abs(sum - 2 * sum2)
+        }
+        console.log(min);
+    })
+}
+```
+
 ### C
 
 前缀和

problems/kamacoder/0047.参会dijkstra堆.md

@@ -911,7 +911,7 @@ func main() {
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ### TypeScript
 

problems/kamacoder/0047.参会dijkstra朴素.md

@@ -867,7 +867,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```js
 function dijkstra(grid, start, end) {

problems/kamacoder/0053.寻宝-Kruskal.md

@@ -547,7 +547,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```js
 function kruskal(v, edges) {

problems/kamacoder/0053.寻宝-prim.md

@@ -692,7 +692,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 ```js
 function prim(v, edges) {
     const grid = Array.from({ length: v + 1 }, () => new Array(v + 1).fill(10001)); // Fixed grid initialization

problems/kamacoder/0055.右旋字符串.md

@@ -350,7 +350,29 @@ function reverseStr(s, start, end) {
 
 
 ### Swift:
+```swift
+func rotateWords(_ s: String, _ k: Int) -> String {
+    var chars = Array(s)
+    // 先反转整体
+    reverseWords(&chars, start: 0, end: s.count - 1)
+    // 反转前半段
+    reverseWords(&chars, start: 0, end: k - 1)
+    // 反转后半段
+    reverseWords(&chars, start: k, end: s.count - 1)
+    return String(chars)
+}
 
+// 反转start...end 的字符数组
+func reverseWords(_ chars: inout [Character], start: Int, end: Int) {
+    var left = start
+    var right = end
+    while left < right, right < chars.count {
+        (chars[left], chars[right]) = (chars[right], chars[left])
+        left += 1
+        right -= 1
+    }
+}
+```
 
 
 ### PHP：

problems/kamacoder/0094.城市间货物运输I-SPFA.md

@@ -462,7 +462,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```js
 async function main() {

problems/kamacoder/0094.城市间货物运输I.md

@@ -483,7 +483,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```js
 async function main() {

problems/kamacoder/0095.城市间货物运输II.md

@@ -333,6 +333,8 @@ public class Main {
 
 ### Python
 
+Bellman-Ford方法求解含有负回路的最短路问题
+
 ```python 
 import sys
 
@@ -388,11 +390,57 @@ if __name__ == "__main__":
 
 ```
 
+SPFA方法求解含有负回路的最短路问题
+
+```python
+from collections import deque
+from math import inf
+
+def main():
+    n, m = [int(i) for i in input().split()]
+    graph = [[] for _ in range(n+1)]
+    min_dist = [inf for _ in range(n+1)]
+    count = [0 for _ in range(n+1)]  # 记录节点加入队列的次数
+    for _ in range(m):
+        s, t, v = [int(i) for i in input().split()]
+        graph[s].append([t, v])
+        
+    min_dist[1] = 0  # 初始化
+    count[1] = 1
+    d = deque([1])
+    flag = False
+    
+    while d:  # 主循环
+        cur_node = d.popleft()
+        for next_node, val in graph[cur_node]:
+            if min_dist[next_node] > min_dist[cur_node] + val:
+                min_dist[next_node] = min_dist[cur_node] + val
+                count[next_node] += 1
+                if next_node not in d:
+                    d.append(next_node)
+                if count[next_node] == n:  # 如果某个点松弛了n次，说明有负回路
+                    flag = True
+        if flag:
+            break
+            
+    if flag:
+        print("circle")
+    else:
+        if min_dist[-1] == inf:
+            print("unconnected")
+        else:
+            print(min_dist[-1])
+
+
+if __name__ == "__main__":
+    main()
+```
+
 ### Go
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ### TypeScript
 

problems/kamacoder/0096.城市间货物运输III.md

@@ -702,7 +702,129 @@ public class Main {
 
 ```
 
+```java
+class Edge {
+    public int u; // 边的端点1
+    public int v; // 边的端点2
+    public int val; // 边的权值
+
+    public Edge() {
+    }
+
+    public Edge(int u, int v) {
+        this.u = u;
+        this.v = v;
+        this.val = 0;
+    }
+
+    public Edge(int u, int v, int val) {
+        this.u = u;
+        this.v = v;
+        this.val = val;
+    }
+}
+
+/**
+ * SPFA算法（版本3）：处理含【负权回路】的有向图的最短路径问题
+ * bellman_ford（版本3） 的队列优化算法版本
+ * 限定起点、终点、至多途径k个节点
+ */
+public class SPFAForSSSP {
+
+    /**
+     * SPFA算法
+     *
+     * @param n        节点个数[1,n]
+     * @param graph    邻接表
+     * @param startIdx 开始节点（源点）
+     */
+    public static int[] spfa(int n, List<List<Edge>> graph, int startIdx, int k) {
+        // 定义最大范围
+        int maxVal = Integer.MAX_VALUE;
+        // minDist[i] 源点到节点i的最短距离
+        int[] minDist = new int[n + 1]; // 有效节点编号范围：[1,n]
+        Arrays.fill(minDist, maxVal); // 初始化为maxVal
+        minDist[startIdx] = 0; // 设置源点到源点的最短路径为0
+
+        // 定义queue记录每一次松弛更新的节点
+        Queue<Integer> queue = new LinkedList<>();
+        queue.offer(startIdx); // 初始化：源点开始（queue和minDist的更新是同步的）
+
+
+        // SPFA算法核心：只对上一次松弛的时候更新过的节点关联的边进行松弛操作
+        while (k + 1 > 0 && !queue.isEmpty()) { // 限定松弛 k+1 次
+            int curSize = queue.size(); // 记录当前队列节点个数（上一次松弛更新的节点个数，用作分层统计）
+            while (curSize-- > 0) { //分层控制，限定本次松弛只针对上一次松弛更新的节点，不对新增的节点做处理
+                // 记录当前minDist状态，作为本次松弛的基础
+                int[] minDist_copy = Arrays.copyOfRange(minDist, 0, minDist.length);
+
+                // 取出节点
+                int cur = queue.poll();
+                // 获取cur节点关联的边，进行松弛操作
+                List<Edge> relateEdges = graph.get(cur);
+                for (Edge edge : relateEdges) {
+                    int u = edge.u; // 与`cur`对照
+                    int v = edge.v;
+                    int weight = edge.val;
+                    if (minDist_copy[u] + weight < minDist[v]) {
+                        minDist[v] = minDist_copy[u] + weight; // 更新
+                        // 队列同步更新（此处有一个针对队列的优化:就是如果已经存在于队列的元素不需要重复添加）
+                        if (!queue.contains(v)) {
+                            queue.offer(v); // 与minDist[i]同步更新，将本次更新的节点加入队列，用做下一个松弛的参考基础
+                        }
+                    }
+                }
+            }
+            // 当次松弛结束，次数-1
+            k--;
+        }
+
+        // 返回minDist
+        return minDist;
+    }
+
+    public static void main(String[] args) {
+        // 输入控制
+        Scanner sc = new Scanner(System.in);
+        System.out.println("1.输入N个节点、M条边（u v weight）");
+        int n = sc.nextInt();
+        int m = sc.nextInt();
+
+        System.out.println("2.输入M条边");
+        List<List<Edge>> graph = new ArrayList<>(); // 构建邻接表
+        for (int i = 0; i <= n; i++) {
+            graph.add(new ArrayList<>());
+        }
+        while (m-- > 0) {
+            int u = sc.nextInt();
+            int v = sc.nextInt();
+            int weight = sc.nextInt();
+            graph.get(u).add(new Edge(u, v, weight));
+        }
+
+        System.out.println("3.输入src dst k（起点、终点、至多途径k个点）");
+        int src = sc.nextInt();
+        int dst = sc.nextInt();
+        int k = sc.nextInt();
+
+        // 调用算法
+        int[] minDist = SPFAForSSSP.spfa(n, graph, src, k);
+        // 校验起点->终点
+        if (minDist[dst] == Integer.MAX_VALUE) {
+            System.out.println("unreachable");
+        } else {
+            System.out.println("最短路径：" + minDist[n]);
+        }
+    }
+}
+```
+
+
+
 ### Python
+
+Bellman-Ford方法求解单源有限最短路
+
 ```python
 def main():
     # 輸入
@@ -736,6 +858,48 @@ def main():
             
             
 
+if __name__ == "__main__":
+    main()
+```
+
+SPFA方法求解单源有限最短路
+
+```python
+from collections import deque
+from math import inf
+
+
+def main():
+    n, m = [int(i) for i in input().split()]
+    graph = [[] for _ in range(n+1)]
+    for _ in range(m):
+        v1, v2, val = [int(i) for i in input().split()]
+        graph[v1].append([v2, val])
+    src, dst, k = [int(i) for i in input().split()]
+    min_dist = [inf for _ in range(n+1)]
+    min_dist[src] = 0  # 初始化起点的距离
+    que = deque([src])
+
+    while k != -1 and que:
+        visited = [False for _ in range(n+1)]  # 用于保证每次松弛时一个节点最多加入队列一次
+        que_size = len(que)
+        temp_dist = min_dist.copy()  # 用于记录上一次遍历的结果
+        for _ in range(que_size):
+            cur_node = que.popleft()
+            for next_node, val in graph[cur_node]:
+                if min_dist[next_node] > temp_dist[cur_node] + val:
+                    min_dist[next_node] = temp_dist[cur_node] + val
+                    if not visited[next_node]:
+                        que.append(next_node)
+                        visited[next_node] = True
+        k -= 1
+
+    if min_dist[dst] == inf:
+        print("unreachable")
+    else:
+        print(min_dist[dst])
+
+
 if __name__ == "__main__":
     main()
 ```
@@ -744,7 +908,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ### TypeScript
 

problems/kamacoder/0097.小明逛公园.md

@@ -425,6 +425,71 @@ floyd算法的时间复杂度相对较高，适合 稠密图且源点较多的
 
 ### Java 
 
+- 基于三维数组的Floyd算法
+
+```java
+public class FloydBase {
+
+    // public static int MAX_VAL = Integer.MAX_VALUE;
+    public static int MAX_VAL = 10005; // 边的最大距离是10^4(不选用Integer.MAX_VALUE是为了避免相加导致数值溢出)
+
+    public static void main(String[] args) {
+        // 输入控制
+        Scanner sc = new Scanner(System.in);
+        System.out.println("1.输入N M");
+        int n = sc.nextInt();
+        int m = sc.nextInt();
+
+        System.out.println("2.输入M条边");
+
+        // ① dp定义（grid[i][j][k] 节点i到节点j 可能经过节点K（k∈[1,n]））的最短路径
+        int[][][] grid = new int[n + 1][n + 1][n + 1];
+        for (int i = 1; i <= n; i++) {
+            for (int j = 1; j <= n; j++) {
+                for (int k = 0; k <= n; k++) {
+                    grid[i][j][k] = grid[j][i][k] = MAX_VAL; // 其余设置为最大值
+                }
+            }
+        }
+
+        // ② dp 推导：grid[i][j][k] = min{grid[i][k][k-1] + grid[k][j][k-1], grid[i][j][k-1]}
+        while (m-- > 0) {
+            int u = sc.nextInt();
+            int v = sc.nextInt();
+            int weight = sc.nextInt();
+            grid[u][v][0] = grid[v][u][0] = weight; // 初始化（处理k=0的情况） ③ dp初始化
+        }
+
+        // ④ dp推导：floyd 推导
+        for (int k = 1; k <= n; k++) {
+            for (int i = 1; i <= n; i++) {
+                for (int j = 1; j <= n; j++) {
+                    grid[i][j][k] = Math.min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1]);
+                }
+            }
+        }
+
+        System.out.println("3.输入[起点-终点]计划个数");
+        int x = sc.nextInt();
+
+        System.out.println("4.输入每个起点src 终点dst");
+
+        while (x-- > 0) {
+            int src = sc.nextInt();
+            int dst = sc.nextInt();
+            // 根据floyd推导结果输出计划路径的最小距离
+            if (grid[src][dst][n] == MAX_VAL) {
+                System.out.println("-1");
+            } else {
+                System.out.println(grid[src][dst][n]);
+            }
+        }
+    }
+}
+```
+
+
+
 ### Python
 
 基于三维数组的Floyd
@@ -493,7 +558,7 @@ if __name__ == '__main__':
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ### TypeScript
 

problems/kamacoder/0098.所有可达路径.md

@@ -726,7 +726,7 @@ func main() {
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 #### 邻接矩阵写法
 

problems/kamacoder/0099.岛屿的数量广搜.md

@@ -254,6 +254,7 @@ directions = [[0, 1], [1, 0], [0, -1], [-1, 0]]
 def bfs(grid, visited, x, y):
     que = deque([])
     que.append([x,y])
+    visited[x][y] = True
     while que:
         cur_x, cur_y = que.popleft()
         for i, j in directions:
@@ -360,7 +361,7 @@ func main() {
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```javascript
 const r1 = require('readline').createInterface({ input: process.stdin });

problems/kamacoder/0099.岛屿的数量深搜.md

@@ -328,7 +328,7 @@ if __name__ == '__main__':
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```javascript
 const r1 = require('readline').createInterface({ input: process.stdin });

problems/kamacoder/0100.岛屿的最大面积.md

@@ -648,7 +648,7 @@ fn main() {
 
 ```
 
-### Javascript
+### JavaScript
 
 ```javascript
 // 广搜版

problems/kamacoder/0101.孤岛的总面积.md

@@ -257,14 +257,62 @@ public class Main {
 
 
 ### Python
+#### 深搜版
+```python
+position = [[1, 0], [0, 1], [-1, 0], [0, -1]]
+count = 0
+
+def dfs(grid, x, y):
+    global count
+    grid[x][y] = 0
+    count += 1
+    for i, j in position:
+        next_x = x + i
+        next_y = y + j
+        if next_x < 0 or next_y < 0 or next_x >= len(grid) or next_y >= len(grid[0]):
+            continue
+        if grid[next_x][next_y] == 1: 
+            dfs(grid, next_x, next_y)
+                
+n, m = map(int, input().split())
+
+# 邻接矩阵
+grid = []
+for i in range(n):
+    grid.append(list(map(int, input().split())))
+
+# 清除边界上的连通分量
+for i in range(n):
+    if grid[i][0] == 1: 
+        dfs(grid, i, 0)
+    if grid[i][m - 1] == 1: 
+        dfs(grid, i, m - 1)
+
+for j in range(m):
+    if grid[0][j] == 1: 
+        dfs(grid, 0, j)
+    if grid[n - 1][j] == 1: 
+        dfs(grid, n - 1, j)
+    
+count = 0 # 将count重置为0
+# 统计内部所有剩余的连通分量
+for i in range(n):
+    for j in range(m):
+        if grid[i][j] == 1:
+            dfs(grid, i, j)
+            
+print(count)
+```
+
+#### 广搜版
 ```python
 from collections import deque
 
 # 处理输入
-n, m = list(map(int, input().strip()))
+n, m = list(map(int, input().split()))
 g = []
 for _ in range(n):
-    row = list(map(int, input().strip()))
+    row = list(map(int, input().split()))
     g.append(row)
 
 # 定义四个方向、孤岛面积（遍历完边缘后会被重置）
@@ -293,17 +341,22 @@ def bfs(r, c):
 
 
 for i in range(n):
-    if g[i][0] == 1: bfs(i, 0)
-    if g[i][m-1] == 1: bfs(i, m-1)
+    if g[i][0] == 1: 
+        bfs(i, 0)
+    if g[i][m-1] == 1: 
+        bfs(i, m-1)
 
 for i in range(m):
-    if g[0][i] == 1: bfs(0, i)
-    if g[n-1][i] == 1: bfs(n-1, i)
+    if g[0][i] == 1: 
+        bfs(0, i)
+    if g[n-1][i] == 1: 
+        bfs(n-1, i)
 
 count = 0
 for i in range(n):
     for j in range(m):
-        if g[i][j] == 1: bfs(i, j)
+        if g[i][j] == 1: 
+            bfs(i, j)
 
 print(count)
 ```
@@ -467,7 +520,7 @@ func main() {
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 #### 深搜版
 

problems/kamacoder/0102.沉没孤岛.md

@@ -322,7 +322,7 @@ for row in g:
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 #### 深搜版
 

problems/kamacoder/0103.水流问题.md

@@ -413,10 +413,85 @@ if __name__ == "__main__":
 ```
 
 ### Go
+```go
+package main
+
+import (
+    "os"
+    "fmt"
+    "strings"
+    "strconv"
+    "bufio"
+)
+
+var directions = [][]int{{0, -1}, {0, 1}, {-1, 0}, {1, 0}} // 四个方向的偏移量
+
+func main() {
+    scanner := bufio.NewScanner(os.Stdin)
+    
+    scanner.Scan()
+    lineList := strings.Fields(scanner.Text())
+    N, _ := strconv.Atoi(lineList[0])
+    M, _ := strconv.Atoi(lineList[1])
+    
+    grid := make([][]int, N)
+    visited := make([][]bool, N) // 用于标记是否访问过
+    for i := 0; i < N; i++ {
+        grid[i] = make([]int, M)
+        visited[i] = make([]bool, M)
+        scanner.Scan()
+        lineList = strings.Fields(scanner.Text())
+        
+        for j := 0; j < M; j++ {
+            grid[i][j], _ = strconv.Atoi(lineList[j])
+        }
+    }
+    
+    // 遍历每个单元格，使用DFS检查是否可达两组边界
+    for i := 0; i < N; i++ {
+        for j := 0; j < M; j++ {
+            canReachFirst, canReachSecond := dfs(grid, visited, i, j)
+            if canReachFirst && canReachSecond {
+                fmt.Println(strconv.Itoa(i) + " " + strconv.Itoa(j))
+            }
+        }
+    }
+}
+
+func dfs(grid [][]int, visited [][]bool, startx int, starty int) (bool, bool) {
+    visited[startx][starty] = true
+    canReachFirst := startx == 0 || starty == 0 || startx == len(grid)-1 || starty == len(grid[0])-1
+    canReachSecond := startx == len(grid)-1 || starty == len(grid[0])-1 || startx == 0 || starty == 0
+    
+    if canReachFirst && canReachSecond {
+        return true, true
+    }
+    
+    for _, direction := range directions {
+        nextx := startx + direction[0]
+        nexty := starty + direction[1]
+        
+        if nextx < 0 || nextx >= len(grid) || nexty < 0 || nexty >= len(grid[0]) {
+            continue
+        }
+        
+        if grid[nextx][nexty] <= grid[startx][starty] && !visited[nextx][nexty] {
+            hasReachFirst, hasReachSecond := dfs(grid, visited, nextx, nexty)
+            if !canReachFirst {
+                canReachFirst = hasReachFirst
+            }
+            if !canReachSecond {
+                canReachSecond = hasReachSecond
+            }
+        }
+    }
+    return canReachFirst, canReachSecond
+}
+```
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 #### 深搜
 

problems/kamacoder/0104.建造最大岛屿.md

@@ -530,7 +530,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```javascript
 const r1 = require('readline').createInterface({ input: process.stdin });

problems/kamacoder/0105.有向图的完全可达性.md

@@ -489,7 +489,55 @@ func main() {
 
 ### Rust
 
-### Javascript
+### JavaScript
+
+```javascript
+const rl = require('readline').createInterface({
+    input:process.stdin,
+    output:process.stdout
+})
+
+let inputLines = []
+
+rl.on('line' , (line)=>{
+    inputLines.push(line)
+})
+
+rl.on('close',()=>{
+    let [n , edgesCount]= inputLines[0].trim().split(' ').map(Number)
+    
+    let graph = Array.from({length:n+1} , ()=>{return[]})
+    
+    for(let i = 1 ; i < inputLines.length ; i++ ){
+        let [from  , to] = inputLines[i].trim().split(' ').map(Number)
+        graph[from].push(to)
+    }
+    
+    let visited = new Array(n + 1).fill(false)
+    
+    let dfs = (graph , key , visited)=>{
+        if(visited[key]){
+            return
+        }
+        
+        visited[key] = true
+        for(let nextKey of graph[key]){
+            dfs(graph,nextKey , visited)
+        }
+    }
+    
+    dfs(graph , 1 , visited)
+    
+    for(let i = 1 ; i <= n;i++){
+        if(visited[i] === false){
+            console.log(-1)
+            return
+        }
+    }
+    console.log(1)
+
+})
+```
 
 ### TypeScript
 

problems/kamacoder/0106.岛屿的周长.md

@@ -343,7 +343,7 @@ func parseLine(line string, count int) []int {
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ### TypeScript
 

problems/kamacoder/0107.寻找存在的路径.md

@@ -340,7 +340,7 @@ func main() {
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```java
 const r1 = require('readline').createInterface({ input: process.stdin });

problems/kamacoder/0108.冗余连接.md

@@ -44,7 +44,7 @@
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240527110320.png)
 
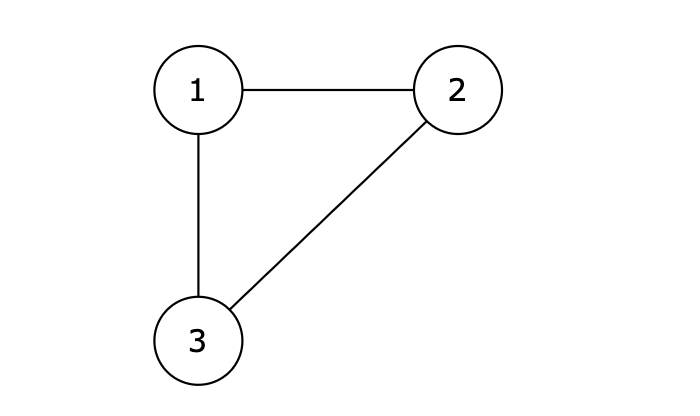
-图中的 1 2，2 3，1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边，所以输出结果为 1 3
+图中的 1 2，2 3，1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输入里最后出现的那条边，所以输出结果为 1 3
 
 数据范围：
 
@@ -221,7 +221,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```javascript
 const r1 = require('readline').createInterface({ input: process.stdin });

problems/kamacoder/0109.冗余连接II.md

@@ -467,7 +467,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```javascript
 const r1 = require('readline').createInterface({ input: process.stdin });

problems/kamacoder/0110.字符串接龙.md

@@ -258,7 +258,7 @@ if __name__=='__main__':
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```javascript
 const r1 = require('readline').createInterface({ input: process.stdin });

problems/kamacoder/0117.软件构建.md

@@ -449,7 +449,7 @@ if __name__ == "__main__":
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```javascript
 const r1 = require('readline').createInterface({ input: process.stdin });

problems/kamacoder/0126.骑士的攻击astar.md

@@ -373,7 +373,7 @@ for _ in range(n):
 
 ### Rust
 
-### Javascript
+### JavaScript
 
 ```js
 class MinHeap {
@@ -514,7 +514,170 @@ main()
 
 ### C
 
-
+```C
+#include <stdio.h>
+#include <stdlib.h>
+#include <string.h>
+
+// 定义一个结构体，表示棋盘上骑士的位置和相关的 A* 算法参数
+typedef struct {
+    int x, y; // 骑士在棋盘上的坐标
+    int g;    // 从起点到当前节点的实际消耗
+    int h;    // 从当前节点到目标节点的估计消耗（启发式函数值）
+    int f;    // 总的估计消耗（f = g + h）
+} Knight;
+
+#define MAX_HEAP_SIZE 2000000 // 假设优先队列的最大容量
+
+// 定义一个优先队列，使用最小堆来实现 A* 算法中的 Open 列表
+typedef struct {
+    Knight data[MAX_HEAP_SIZE];
+    int size;
+} PriorityQueue;
+
+// 初始化优先队列
+void initQueue(PriorityQueue *pq) {
+    pq->size = 0;
+}
+
+// 将骑士节点插入优先队列
+void push(PriorityQueue *pq, Knight k) {
+    if (pq->size >= MAX_HEAP_SIZE) {
+        // 堆已满，无法插入新节点
+        return;
+    }
+    int i = pq->size++;
+    pq->data[i] = k;
+    // 上滤操作，维护最小堆的性质，使得 f 值最小的节点在堆顶
+    while (i > 0) {
+        int parent = (i - 1) / 2;
+        if (pq->data[parent].f <= pq->data[i].f) {
+            break;
+        }
+        // 交换父节点和当前节点
+        Knight temp = pq->data[parent];
+        pq->data[parent] = pq->data[i];
+        pq->data[i] = temp;
+        i = parent;
+    }
+}
+
+// 从优先队列中弹出 f 值最小的骑士节点
+Knight pop(PriorityQueue *pq) {
+    Knight min = pq->data[0];
+    pq->size--;
+    pq->data[0] = pq->data[pq->size];
+    // 下滤操作，维护最小堆的性质
+    int i = 0;
+    while (1) {
+        int left = 2 * i + 1;
+        int right = 2 * i + 2;
+        int smallest = i;
+        if (left < pq->size && pq->data[left].f < pq->data[smallest].f) {
+            smallest = left;
+        }
+        if (right < pq->size && pq->data[right].f < pq->data[smallest].f) {
+            smallest = right;
+        }
+        if (smallest == i) {
+            break;
+        }
+        // 交换当前节点与最小子节点
+        Knight temp = pq->data[smallest];
+        pq->data[smallest] = pq->data[i];
+        pq->data[i] = temp;
+        i = smallest;
+    }
+    return min;
+}
+
+// 判断优先队列是否为空
+int isEmpty(PriorityQueue *pq) {
+    return pq->size == 0;
+}
+
+// 启发式函数：计算从当前位置到目标位置的欧几里得距离的平方（避免开方，提高效率）
+int heuristic(int x, int y, int goal_x, int goal_y) {
+    int dx = x - goal_x;
+    int dy = y - goal_y;
+    return dx * dx + dy * dy; // 欧几里得距离的平方
+}
+
+// 用于记录从起点到棋盘上每个位置的最小移动次数
+int moves[1001][1001];
+
+// 骑士在棋盘上的8个可能移动方向
+int dir[8][2] = {
+    {-2, -1}, {-2, 1}, {-1, 2}, {1, 2},
+    {2, 1}, {2, -1}, {1, -2}, {-1, -2}
+};
+
+// 使用 A* 算法寻找从起点到目标点的最短路径
+int astar(int start_x, int start_y, int goal_x, int goal_y) {
+    PriorityQueue pq;
+    initQueue(&pq);
+
+    // 初始化 moves 数组，-1 表示未访问过的位置
+    memset(moves, -1, sizeof(moves));
+    moves[start_x][start_y] = 0; // 起点位置的移动次数为 0
+
+    // 初始化起始节点
+    Knight start;
+    start.x = start_x;
+    start.y = start_y;
+    start.g = 0; 
+    start.h = heuristic(start_x, start_y, goal_x, goal_y);
+    start.f = start.g + start.h; // 总的估计消耗
+
+    push(&pq, start); // 将起始节点加入优先队列
+
+    while (!isEmpty(&pq)) {
+        Knight current = pop(&pq); // 取出 f 值最小的节点
+
+        // 如果已经到达目标位置，返回所需的最小移动次数
+        if (current.x == goal_x && current.y == goal_y) {
+            return moves[current.x][current.y];
+        }
+
+        // 遍历当前节点的所有可能移动方向
+        for (int i = 0; i < 8; i++) {
+            int nx = current.x + dir[i][0];
+            int ny = current.y + dir[i][1];
+
+            // 检查新位置是否在棋盘范围内且未被访问过
+            if (nx >= 1 && nx <= 1000 && ny >= 1 && ny <= 1000 && moves[nx][ny] == -1) {
+                moves[nx][ny] = moves[current.x][current.y] + 1; // 更新移动次数
+
+                // 创建新节点，表示骑士移动到的新位置
+                Knight neighbor;
+                neighbor.x = nx;
+                neighbor.y = ny;
+                neighbor.g = current.g + 5; // 每次移动的消耗为 5（骑士移动的距离平方）
+                neighbor.h = heuristic(nx, ny, goal_x, goal_y);
+                neighbor.f = neighbor.g + neighbor.h;
+
+                push(&pq, neighbor); // 将新节点加入优先队列
+            }
+        }
+    }
+
+    return -1; // 如果无法到达目标位置，返回 -1
+}
+
+int main() {
+    int n; 
+    scanf("%d", &n);
+    while (n--) {
+        int a1, a2, b1, b2; // 起点和目标点的坐标
+        scanf("%d %d %d %d", &a1, &a2, &b1, &b2);
+
+        int result = astar(a1, a2, b1, b2); // 使用 A* 算法计算最短路径
+        printf("%d\n", result); // 输出最小移动次数
+    }
+    return 0;
+}
+
+```