mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2026-02-02 18:39:09 +08:00
Update
This commit is contained in:
@@ -17,21 +17,15 @@
|
||||
|
||||
## 思路
|
||||
|
||||
正式开始讲解背包问题!
|
||||
|
||||
这周我们正式开始讲解背包问题!
|
||||
|
||||
背包问题的经典资料当然是:背包九讲。在公众号「代码随想录」后台回复:背包九讲,就可以获得背包九讲的pdf。
|
||||
|
||||
但说实话,背包九讲对于小白来说确实不太友好,看起来还是有点费劲的,而且都是伪代码理解起来也吃力。
|
||||
|
||||
对于面试的话,其实掌握01背包,和完全背包,就够用了,最多可以再来一个多重背包。
|
||||
对于面试的话,其实掌握01背包和完全背包,就够用了,最多可以再来一个多重背包。
|
||||
|
||||
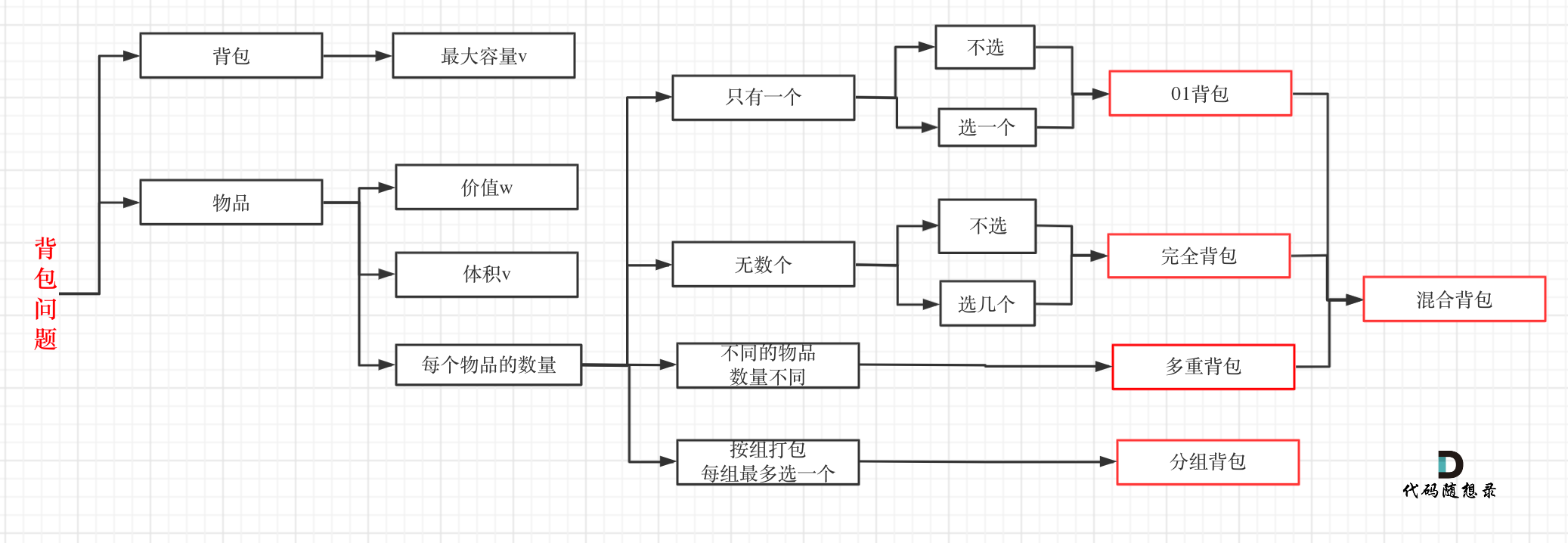
如果这几种背包,分不清,我这里画了一个图,如下:
|
||||
|
||||
|
||||
|
||||
|
||||
至于背包九讲其他背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了。
|
||||
除此以外其他类型的背包,面试几乎不会问,都是竞赛级别的了,leetcode上连多重背包的题目都没有,所以题库也告诉我们,01背包和完全背包就够用了。
|
||||
|
||||
而完全背包又是也是01背包稍作变化而来,即:完全背包的物品数量是无限的。
|
||||
|
||||
@@ -53,7 +47,7 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
|
||||
|
||||
这样其实是没有从底向上去思考,而是习惯性想到了背包,那么暴力的解法应该是怎么样的呢?
|
||||
|
||||
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是$o(2^n)$,这里的n表示物品数量。
|
||||
每一件物品其实只有两个状态,取或者不取,所以可以使用回溯法搜索出所有的情况,那么时间复杂度就是O(2^n),这里的n表示物品数量。
|
||||
|
||||
**所以暴力的解法是指数级别的时间复杂度。进而才需要动态规划的解法来进行优化!**
|
||||
|
||||
@@ -73,30 +67,111 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
|
||||
|
||||
以下讲解和图示中出现的数字都是以这个例子为例。
|
||||
|
||||
|
||||
### 二维dp数组01背包
|
||||
|
||||
依然动规五部曲分析一波。
|
||||
|
||||
1. 确定dp数组以及下标的含义
|
||||
|
||||
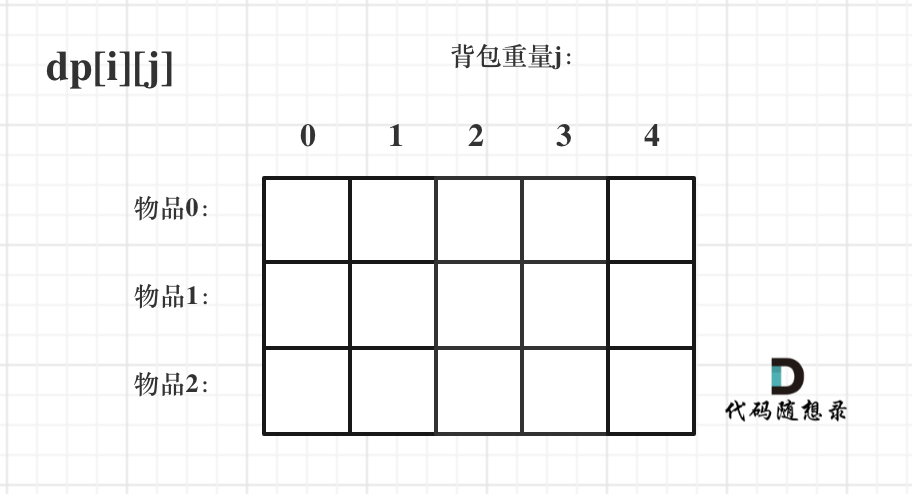
对于背包问题,有一种写法, 是使用二维数组,即**dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少**。
|
||||
我们需要使用二维数组,为什么呢?
|
||||
|
||||
只看这个二维数组的定义,大家一定会有点懵,看下面这个图:
|
||||
因为有两个维度需要表示,分别是:物品 和 背包容量
|
||||
|
||||
如图,二维数组为 dp[i][j]。
|
||||
|
||||
|
||||
|
||||
那么这里 i 、j、dp[i][j] 分别表示什么呢?
|
||||
|
||||
i 来表示物品、j表示背包容量。
|
||||
|
||||
(如果想用j 表示物品,j表示背包容量 行不行? 都可以的,个人习惯而已)
|
||||
|
||||
我们来尝试把上面的 二维表格填写一下。
|
||||
|
||||
动态规划的思路是根据子问题的求解推导出整体的最优解。
|
||||
|
||||
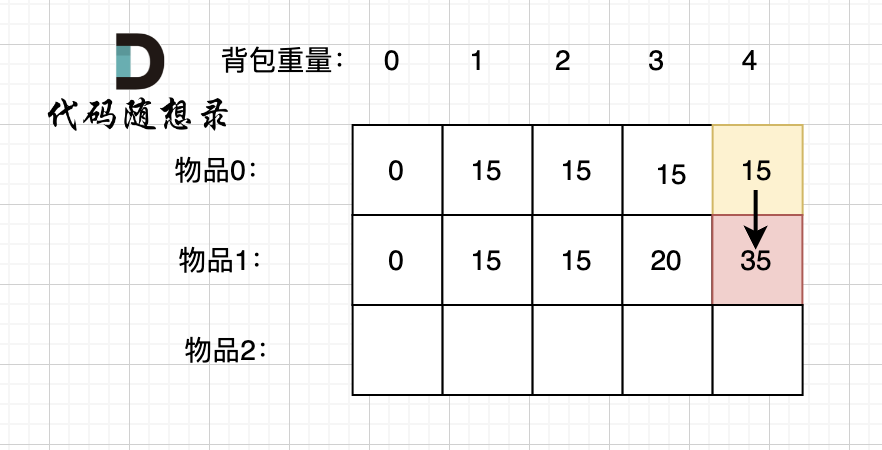
我们先看把物品0 放入背包的情况:
|
||||
|
||||

|
||||
|
||||
背包容量为0,放不下物品0,此时背包里的价值为0。
|
||||
|
||||
背包容量为1,可以放下物品0,此时背包里的价值为15.
|
||||
|
||||
背包容量为2,依然可以放下物品0 (注意 01背包里物品只有一个),此时背包里的价值为15。
|
||||
|
||||
以此类推。
|
||||
|
||||
再看把物品1 放入背包:
|
||||
|
||||

|
||||
|
||||
背包容量为 0,放不下物品0 或者物品1,此时背包里的价值为0。
|
||||
|
||||
背包容量为 1,只能放下物品1,背包里的价值为15。
|
||||
|
||||
背包容量为 2,只能放下物品1,背包里的价值为15。
|
||||
|
||||
背包容量为 3,上一行同一状态,背包只能放物品0,这次也可以选择物品1了,背包可以放物品2 或者 物品1,物品2价值更大,背包里的价值为20。
|
||||
|
||||
背包容量为 4,上一行同一状态,背包只能放物品0,这次也可以选择物品1了,背包都可都放下,背包价值为35。
|
||||
|
||||
以上举例,是比较容易看懂,我主要是通过这个例子,来帮助大家明确dp数组的含义。
|
||||
|
||||
上图中,我们看 dp[1][4] 表示什么意思呢。
|
||||
|
||||
任取 物品0,物品1 放进容量为4的背包里,最大价值是 dp[1][4]。
|
||||
|
||||
通过这个举例,我们来进一步明确dp数组的含义。
|
||||
|
||||
即**dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少**。
|
||||
|
||||
**要时刻记着这个dp数组的含义,下面的一些步骤都围绕这dp数组的含义进行的**,如果哪里看懵了,就来回顾一下i代表什么,j又代表什么。
|
||||
|
||||
2. 确定递推公式
|
||||
|
||||
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
|
||||
这里在把基本信息给出来:
|
||||
|
||||
那么可以有两个方向推出来dp[i][j],
|
||||
| | 重量 | 价值 |
|
||||
| ----- | ---- | ---- |
|
||||
| 物品0 | 1 | 15 |
|
||||
| 物品1 | 3 | 20 |
|
||||
| 物品2 | 4 | 30 |
|
||||
|
||||
对于递推公式,首先我们要明确有哪些方向可以推导出 dp[i][j]。
|
||||
|
||||
这里我们dp[1][4]的状态来举例:
|
||||
|
||||
绝对 dp[1][4],就是放物品1 ,还是不放物品1。
|
||||
|
||||
如果不放物品1, 那么背包的价值应该是 dp[0][4] 即 容量为4的背包,只放物品0的情况。
|
||||
|
||||
推导方向如图:
|
||||
|
||||
|
||||
|
||||
|
||||
如果放物品1, **那么背包要先留出物品1的容量**,目前容量是4,物品1 需要重量为3,此时背包剩下容量为1。
|
||||
|
||||
容量为1,只考虑放物品0 的最大价值是 dp[0][1],这个值我们之前就计算过。
|
||||
|
||||
所以 放物品1 的情况 = dp[0][1] + 物品1 的重量,推导方向如图:
|
||||
|
||||

|
||||
|
||||
两种情况,分别是放物品1 和 不放物品1,我们要取最大值(毕竟求的是最大价值)
|
||||
|
||||
`dp[1][4] = max(dp[0][4], dp[0][1] + 物品1 的重量) `
|
||||
|
||||
以上过程,抽象化如下:
|
||||
|
||||
* **不放物品i**:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。
|
||||
|
||||
* **不放物品i**:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
|
||||
* **放物品i**:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
|
||||
|
||||
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
递归公式: `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);`
|
||||
|
||||
3. dp数组如何初始化
|
||||
|
||||
@@ -108,13 +183,13 @@ leetcode上没有纯01背包的问题,都是01背包应用方面的题目,
|
||||
|
||||
在看其他情况。
|
||||
|
||||
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
|
||||
状态转移方程 `dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);` 可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
|
||||
|
||||
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
|
||||
|
||||
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
|
||||
那么很明显当 `j < weight[0]`的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
|
||||
|
||||
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
|
||||
当`j >= weight[0]`时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
|
||||
|
||||
代码初始化如下:
|
||||
|
||||
@@ -147,7 +222,7 @@ dp[0][j] 和 dp[i][0] 都已经初始化了,那么其他下标应该初始化
|
||||
|
||||
最后初始化代码如下:
|
||||
|
||||
```
|
||||
```CPP
|
||||
// 初始化 dp
|
||||
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
@@ -171,7 +246,7 @@ for (int j = weight[0]; j <= bagweight; j++) {
|
||||
|
||||
那么我先给出先遍历物品,然后遍历背包重量的代码。
|
||||
|
||||
```
|
||||
```CPP
|
||||
// weight数组的大小 就是物品个数
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
|
||||
@@ -186,7 +261,7 @@ for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
|
||||
例如这样:
|
||||
|
||||
```
|
||||
```CPP
|
||||
// weight数组的大小 就是物品个数
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
@@ -200,7 +275,7 @@ for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
|
||||
|
||||
**要理解递归的本质和递推的方向**。
|
||||
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
|
||||
`dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);` 递归公式中可以看出dp[i][j]是靠dp[i-1][j]和dp[i - 1][j - weight[i]]推导出来的。
|
||||
|
||||
dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括正上方向),那么先遍历物品,再遍历背包的过程如图所示:
|
||||
|
||||
@@ -232,50 +307,20 @@ dp[i-1][j]和dp[i - 1][j - weight[i]] 都在dp[i][j]的左上角方向(包括
|
||||
|
||||
主要就是自己没有动手推导一下dp数组的演变过程,如果推导明白了,代码写出来就算有问题,只要把dp数组打印出来,对比一下和自己推导的有什么差异,很快就可以发现问题了。
|
||||
|
||||
```cpp
|
||||
void test_2_wei_bag_problem1() {
|
||||
vector<int> weight = {1, 3, 4};
|
||||
vector<int> value = {15, 20, 30};
|
||||
int bagweight = 4;
|
||||
|
||||
// 二维数组
|
||||
vector<vector<int>> dp(weight.size(), vector<int>(bagweight + 1, 0));
|
||||
|
||||
// 初始化
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// weight数组的大小 就是物品个数
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历物品
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历背包容量
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
|
||||
}
|
||||
}
|
||||
|
||||
cout << dp[weight.size() - 1][bagweight] << endl;
|
||||
}
|
||||
|
||||
int main() {
|
||||
test_2_wei_bag_problem1();
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
本题力扣上没有原题,大家可以去[卡码网第46题](https://kamacoder.com/problempage.php?pid=1046)去练习,题意是一样的,代码如下:
|
||||
|
||||
```CPP
|
||||
|
||||
//二维dp数组实现
|
||||
#include <bits/stdc++.h>
|
||||
using namespace std;
|
||||
|
||||
int n, bagweight;// bagweight代表行李箱空间
|
||||
void solve() {
|
||||
int main() {
|
||||
int n, bagweight;// bagweight代表行李箱空间
|
||||
|
||||
cin >> n >> bagweight;
|
||||
|
||||
vector<int> weight(n, 0); // 存储每件物品所占空间
|
||||
vector<int> value(n, 0); // 存储每件物品价值
|
||||
|
||||
for(int i = 0; i < n; ++i) {
|
||||
cin >> weight[i];
|
||||
}
|
||||
@@ -294,33 +339,28 @@ void solve() {
|
||||
|
||||
for(int i = 1; i < weight.size(); i++) { // 遍历科研物品
|
||||
for(int j = 0; j <= bagweight; j++) { // 遍历行李箱容量
|
||||
// 如果装不下这个物品,那么就继承dp[i - 1][j]的值
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
// 如果能装下,就将值更新为 不装这个物品的最大值 和 装这个物品的最大值 中的 最大值
|
||||
// 装这个物品的最大值由容量为j - weight[i]的包任意放入序号为[0, i - 1]的最大值 + 该物品的价值构成
|
||||
else dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
if (j < weight[i]) dp[i][j] = dp[i - 1][j]; // 如果装不下这个物品,那么就继承dp[i - 1][j]的值
|
||||
else {
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
cout << dp[weight.size() - 1][bagweight] << endl;
|
||||
}
|
||||
cout << dp[n - 1][bagweight] << endl;
|
||||
|
||||
int main() {
|
||||
while(cin >> n >> bagweight) {
|
||||
solve();
|
||||
}
|
||||
return 0;
|
||||
}
|
||||
|
||||
|
||||
```
|
||||
|
||||
|
||||
## 总结
|
||||
|
||||
讲了这么多才刚刚把二维dp的01背包讲完,**这里大家其实可以发现最简单的是推导公式了,推导公式估计看一遍就记下来了,但难就难在如何初始化和遍历顺序上**。
|
||||
背包问题 是动态规划里的经典类型题目,大家要细细品味。
|
||||
|
||||
可能有的同学并没有注意到初始化 和 遍历顺序的重要性,我们后面做力扣上背包面试题目的时候,大家就会感受出来了。
|
||||
|
||||
下一篇 还是理论基础,我们再来讲一维dp数组实现的01背包(滚动数组),分析一下和二维有什么区别,在初始化和遍历顺序上又有什么差异,敬请期待!
|
||||
下一篇 还是理论基础,我们再来讲一维dp数组实现的01背包(滚动数组),分析一下和二维有什么区别,在初始化和遍历顺序上又有什么差异。
|
||||
|
||||
|
||||
|
||||
@@ -329,120 +369,42 @@ int main() {
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
public class BagProblem {
|
||||
```Java
|
||||
import java.util.Scanner;
|
||||
|
||||
public class Main {
|
||||
public static void main(String[] args) {
|
||||
int[] weight = {1,3,4};
|
||||
int[] value = {15,20,30};
|
||||
int bagSize = 4;
|
||||
testWeightBagProblem(weight,value,bagSize);
|
||||
}
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int bagweight = scanner.nextInt();
|
||||
|
||||
/**
|
||||
* 动态规划获得结果
|
||||
* @param weight 物品的重量
|
||||
* @param value 物品的价值
|
||||
* @param bagSize 背包的容量
|
||||
*/
|
||||
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
|
||||
int[] weight = new int[n];
|
||||
int[] value = new int[n];
|
||||
|
||||
// 创建dp数组
|
||||
int goods = weight.length; // 获取物品的数量
|
||||
int[][] dp = new int[goods][bagSize + 1];
|
||||
for (int i = 0; i < n; ++i) {
|
||||
weight[i] = scanner.nextInt();
|
||||
}
|
||||
for (int j = 0; j < n; ++j) {
|
||||
value[j] = scanner.nextInt();
|
||||
}
|
||||
|
||||
// 初始化dp数组
|
||||
// 创建数组后,其中默认的值就是0
|
||||
for (int j = weight[0]; j <= bagSize; j++) {
|
||||
int[][] dp = new int[n][bagweight + 1];
|
||||
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// 填充dp数组
|
||||
for (int i = 1; i < weight.length; i++) {
|
||||
for (int j = 1; j <= bagSize; j++) {
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
/**
|
||||
* 当前背包的容量都没有当前物品i大的时候,是不放物品i的
|
||||
* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
|
||||
*/
|
||||
dp[i][j] = dp[i-1][j];
|
||||
} else {
|
||||
/**
|
||||
* 当前背包的容量可以放下物品i
|
||||
* 那么此时分两种情况:
|
||||
* 1、不放物品i
|
||||
* 2、放物品i
|
||||
* 比较这两种情况下,哪种背包中物品的最大价值最大
|
||||
*/
|
||||
dp[i][j] = Math.max(dp[i-1][j] , dp[i-1][j-weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 打印dp数组
|
||||
for (int i = 0; i < goods; i++) {
|
||||
for (int j = 0; j <= bagSize; j++) {
|
||||
System.out.print(dp[i][j] + "\t");
|
||||
}
|
||||
System.out.println("\n");
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
```java
|
||||
import java.util.Arrays;
|
||||
|
||||
public class BagProblem {
|
||||
public static void main(String[] args) {
|
||||
int[] weight = {1,3,4};
|
||||
int[] value = {15,20,30};
|
||||
int bagSize = 4;
|
||||
testWeightBagProblem(weight,value,bagSize);
|
||||
}
|
||||
|
||||
/**
|
||||
* 初始化 dp 数组做了简化(给物品增加冗余维)。这样初始化dp数组,默认全为0即可。
|
||||
* dp[i][j] 表示从下标为[0 - i-1]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
|
||||
* 其实是模仿背包重量从 0 开始,背包容量 j 为 0 的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为 0。
|
||||
* 可选物品也可以从无开始,也就是没有物品可选,即dp[0][j],这样无论背包容量为多少,背包价值总和一定为 0。
|
||||
* @param weight 物品的重量
|
||||
* @param value 物品的价值
|
||||
* @param bagSize 背包的容量
|
||||
*/
|
||||
public static void testWeightBagProblem(int[] weight, int[] value, int bagSize){
|
||||
|
||||
// 创建dp数组
|
||||
int goods = weight.length; // 获取物品的数量
|
||||
int[][] dp = new int[goods + 1][bagSize + 1]; // 给物品增加冗余维,i = 0 表示没有物品可选
|
||||
|
||||
// 初始化dp数组,默认全为0即可
|
||||
// 填充dp数组
|
||||
for (int i = 1; i <= goods; i++) {
|
||||
for (int j = 1; j <= bagSize; j++) {
|
||||
if (j < weight[i - 1]) { // i - 1 对应物品 i
|
||||
/**
|
||||
* 当前背包的容量都没有当前物品i大的时候,是不放物品i的
|
||||
* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值
|
||||
*/
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
/**
|
||||
* 当前背包的容量可以放下物品i
|
||||
* 那么此时分两种情况:
|
||||
* 1、不放物品i
|
||||
* 2、放物品i
|
||||
* 比较这两种情况下,哪种背包中物品的最大价值最大
|
||||
*/
|
||||
dp[i][j] = Math.max(dp[i - 1][j] , dp[i - 1][j - weight[i - 1]] + value[i - 1]); // i - 1 对应物品 i
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 打印dp数组
|
||||
for(int[] arr : dp){
|
||||
System.out.println(Arrays.toString(arr));
|
||||
}
|
||||
System.out.println(dp[n - 1][bagweight]);
|
||||
}
|
||||
}
|
||||
|
||||
@@ -450,137 +412,71 @@ public class BagProblem {
|
||||
|
||||
### Python
|
||||
|
||||
无参数版
|
||||
```python
|
||||
def test_2_wei_bag_problem1():
|
||||
weight = [1, 3, 4]
|
||||
value = [15, 20, 30]
|
||||
bagweight = 4
|
||||
n, bagweight = map(int, input().split())
|
||||
|
||||
# 二维数组
|
||||
dp = [[0] * (bagweight + 1) for _ in range(len(weight))]
|
||||
weight = list(map(int, input().split()))
|
||||
value = list(map(int, input().split()))
|
||||
|
||||
# 初始化
|
||||
for j in range(weight[0], bagweight + 1):
|
||||
dp[0][j] = value[0]
|
||||
dp = [[0] * (bagweight + 1) for _ in range(n)]
|
||||
|
||||
# weight数组的大小就是物品个数
|
||||
for i in range(1, len(weight)): # 遍历物品
|
||||
for j in range(bagweight + 1): # 遍历背包容量
|
||||
if j < weight[i]:
|
||||
dp[i][j] = dp[i - 1][j]
|
||||
else:
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
|
||||
for j in range(weight[0], bagweight + 1):
|
||||
dp[0][j] = value[0]
|
||||
|
||||
print(dp[len(weight) - 1][bagweight])
|
||||
|
||||
test_2_wei_bag_problem1()
|
||||
|
||||
```
|
||||
有参数版
|
||||
```python
|
||||
def test_2_wei_bag_problem1(weight, value, bagweight):
|
||||
# 二维数组
|
||||
dp = [[0] * (bagweight + 1) for _ in range(len(weight))]
|
||||
|
||||
# 初始化
|
||||
for j in range(weight[0], bagweight + 1):
|
||||
dp[0][j] = value[0]
|
||||
|
||||
# weight数组的大小就是物品个数
|
||||
for i in range(1, len(weight)): # 遍历物品
|
||||
for j in range(bagweight + 1): # 遍历背包容量
|
||||
if j < weight[i]:
|
||||
dp[i][j] = dp[i - 1][j]
|
||||
else:
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
|
||||
|
||||
return dp[len(weight) - 1][bagweight]
|
||||
|
||||
if __name__ == "__main__":
|
||||
|
||||
weight = [1, 3, 4]
|
||||
value = [15, 20, 30]
|
||||
bagweight = 4
|
||||
|
||||
result = test_2_wei_bag_problem1(weight, value, bagweight)
|
||||
print(result)
|
||||
for i in range(1, n):
|
||||
for j in range(bagweight + 1):
|
||||
if j < weight[i]:
|
||||
dp[i][j] = dp[i - 1][j]
|
||||
else:
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i])
|
||||
|
||||
print(dp[n - 1][bagweight])
|
||||
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
```go
|
||||
func test_2_wei_bag_problem1(weight, value []int, bagweight int) int {
|
||||
// 定义dp数组
|
||||
dp := make([][]int, len(weight))
|
||||
for i, _ := range dp {
|
||||
dp[i] = make([]int, bagweight+1)
|
||||
}
|
||||
// 初始化
|
||||
for j := bagweight; j >= weight[0]; j-- {
|
||||
dp[0][j] = dp[0][j-weight[0]] + value[0]
|
||||
}
|
||||
// 递推公式
|
||||
for i := 1; i < len(weight); i++ {
|
||||
//正序,也可以倒序
|
||||
for j := 0; j <= bagweight; j++ {
|
||||
if j < weight[i] {
|
||||
dp[i][j] = dp[i-1][j]
|
||||
} else {
|
||||
dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i])
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[len(weight)-1][bagweight]
|
||||
}
|
||||
|
||||
func max(a,b int) int {
|
||||
if a > b {
|
||||
return a
|
||||
}
|
||||
return b
|
||||
}
|
||||
|
||||
func main() {
|
||||
weight := []int{1,3,4}
|
||||
value := []int{15,20,30}
|
||||
test_2_wei_bag_problem1(weight,value,4)
|
||||
}
|
||||
```
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
function testWeightBagProblem (weight, value, size) {
|
||||
// 定义 dp 数组
|
||||
const len = weight.length,
|
||||
dp = Array(len).fill().map(() => Array(size + 1).fill(0));
|
||||
const readline = require('readline').createInterface({
|
||||
input: process.stdin,
|
||||
output: process.stdout
|
||||
});
|
||||
|
||||
// 初始化
|
||||
for(let j = weight[0]; j <= size; j++) {
|
||||
let input = [];
|
||||
|
||||
readline.on('line', (line) => {
|
||||
input.push(line);
|
||||
});
|
||||
|
||||
readline.on('close', () => {
|
||||
let [n, bagweight] = input[0].split(' ').map(Number);
|
||||
let weight = input[1].split(' ').map(Number);
|
||||
let value = input[2].split(' ').map(Number);
|
||||
|
||||
let dp = Array.from({ length: n }, () => Array(bagweight + 1).fill(0));
|
||||
|
||||
for (let j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// weight 数组的长度len 就是物品个数
|
||||
for(let i = 1; i < len; i++) { // 遍历物品
|
||||
for(let j = 0; j <= size; j++) { // 遍历背包容量
|
||||
if(j < weight[i]) dp[i][j] = dp[i - 1][j];
|
||||
else dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
for (let i = 1; i < n; i++) {
|
||||
for (let j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
console.table(dp)
|
||||
console.log(dp[n - 1][bagweight]);
|
||||
});
|
||||
|
||||
return dp[len - 1][size];
|
||||
}
|
||||
|
||||
function test () {
|
||||
console.log(testWeightBagProblem([1, 3, 4, 5], [15, 20, 30, 55], 6));
|
||||
}
|
||||
|
||||
test();
|
||||
```
|
||||
|
||||
|
||||
@@ -589,158 +485,63 @@ test();
|
||||
```c
|
||||
#include <stdio.h>
|
||||
#include <stdlib.h>
|
||||
#include <string.h>
|
||||
|
||||
#define MAX(a, b) (((a) > (b)) ? (a) : (b))
|
||||
#define ARR_SIZE(a) (sizeof((a)) / sizeof((a)[0]))
|
||||
#define BAG_WEIGHT 4
|
||||
int max(int a, int b) {
|
||||
return a > b ? a : b;
|
||||
}
|
||||
|
||||
void backPack(int* weights, int weightSize, int* costs, int costSize, int bagWeight) {
|
||||
// 开辟dp数组
|
||||
int dp[weightSize][bagWeight + 1];
|
||||
memset(dp, 0, sizeof(int) * weightSize * (bagWeight + 1));
|
||||
int main() {
|
||||
int n, bagweight;
|
||||
scanf("%d %d", &n, &bagweight);
|
||||
|
||||
int i, j;
|
||||
// 当背包容量大于物品0的重量时,将物品0放入到背包中
|
||||
for(j = weights[0]; j <= bagWeight; ++j) {
|
||||
dp[0][j] = costs[0];
|
||||
int *weight = (int *)malloc(n * sizeof(int));
|
||||
int *value = (int *)malloc(n * sizeof(int));
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
scanf("%d", &weight[i]);
|
||||
}
|
||||
for (int j = 0; j < n; ++j) {
|
||||
scanf("%d", &value[j]);
|
||||
}
|
||||
|
||||
// 先遍历物品,再遍历重量
|
||||
for(j = 1; j <= bagWeight; ++j) {
|
||||
for(i = 1; i < weightSize; ++i) {
|
||||
// 如果当前背包容量小于物品重量
|
||||
if(j < weights[i])
|
||||
// 背包物品的价值等于背包不放置当前物品时的价值
|
||||
dp[i][j] = dp[i-1][j];
|
||||
// 若背包当前重量可以放置物品
|
||||
else
|
||||
// 背包的价值等于放置该物品或不放置该物品的最大值
|
||||
dp[i][j] = MAX(dp[i - 1][j], dp[i - 1][j - weights[i]] + costs[i]);
|
||||
int **dp = (int **)malloc(n * sizeof(int *));
|
||||
for (int i = 0; i < n; ++i) {
|
||||
dp[i] = (int *)malloc((bagweight + 1) * sizeof(int));
|
||||
for (int j = 0; j <= bagweight; ++j) {
|
||||
dp[i][j] = 0;
|
||||
}
|
||||
}
|
||||
|
||||
printf("%d\n", dp[weightSize - 1][bagWeight]);
|
||||
}
|
||||
|
||||
int main(int argc, char* argv[]) {
|
||||
int weights[] = {1, 3, 4};
|
||||
int costs[] = {15, 20, 30};
|
||||
backPack(weights, ARR_SIZE(weights), costs, ARR_SIZE(costs), BAG_WEIGHT);
|
||||
return 0;
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
### TypeScript
|
||||
|
||||
```typescript
|
||||
function testWeightBagProblem(
|
||||
weight: number[],
|
||||
value: number[],
|
||||
size: number
|
||||
): number {
|
||||
/**
|
||||
* dp[i][j]: 前i个物品,背包容量为j,能获得的最大价值
|
||||
* dp[0][*]: u=weight[0],u之前为0,u之后(含u)为value[0]
|
||||
* dp[*][0]: 0
|
||||
* ...
|
||||
* dp[i][j]: max(dp[i-1][j], dp[i-1][j-weight[i]]+value[i]);
|
||||
*/
|
||||
const goodsNum: number = weight.length;
|
||||
const dp: number[][] = new Array(goodsNum)
|
||||
.fill(0)
|
||||
.map((_) => new Array(size + 1).fill(0));
|
||||
for (let i = weight[0]; i <= size; i++) {
|
||||
dp[0][i] = value[0];
|
||||
}
|
||||
for (let i = 1; i < goodsNum; i++) {
|
||||
for (let j = 1; j <= size; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
}
|
||||
return dp[goodsNum - 1][size];
|
||||
}
|
||||
// test
|
||||
const weight = [1, 3, 4];
|
||||
const value = [15, 20, 30];
|
||||
const size = 4;
|
||||
console.log(testWeightBagProblem(weight, value, size));
|
||||
```
|
||||
|
||||
### Scala
|
||||
|
||||
```scala
|
||||
object Solution {
|
||||
// 01背包
|
||||
def test_2_wei_bag_problem1(): Unit = {
|
||||
var weight = Array[Int](1, 3, 4)
|
||||
var value = Array[Int](15, 20, 30)
|
||||
var baseweight = 4
|
||||
|
||||
// 二维数组
|
||||
var dp = Array.ofDim[Int](weight.length, baseweight + 1)
|
||||
|
||||
// 初始化
|
||||
for (j <- weight(0) to baseweight) {
|
||||
dp(0)(j) = value(0)
|
||||
for (int j = weight[0]; j <= bagweight; j++) {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
// 遍历
|
||||
for (i <- 1 until weight.length; j <- 1 to baseweight) {
|
||||
if (j - weight(i) >= 0) dp(i)(j) = dp(i - 1)(j - weight(i)) + value(i)
|
||||
dp(i)(j) = math.max(dp(i)(j), dp(i - 1)(j))
|
||||
}
|
||||
|
||||
// 打印数组
|
||||
dp.foreach(x => println("[" + x.mkString(",") + "]"))
|
||||
|
||||
dp(weight.length - 1)(baseweight) // 最终返回
|
||||
}
|
||||
|
||||
def main(args: Array[String]): Unit = {
|
||||
test_2_wei_bag_problem1()
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### Rust
|
||||
|
||||
```rust
|
||||
pub struct Solution;
|
||||
|
||||
impl Solution {
|
||||
pub fn wei_bag_problem1(weight: Vec<usize>, value: Vec<usize>, bag_size: usize) -> usize {
|
||||
let mut dp = vec![vec![0; bag_size + 1]; weight.len()];
|
||||
for j in weight[0]..=weight.len() {
|
||||
dp[0][j] = value[0];
|
||||
}
|
||||
|
||||
for i in 1..weight.len() {
|
||||
for j in 0..=bag_size {
|
||||
match j < weight[i] {
|
||||
true => dp[i][j] = dp[i - 1][j],
|
||||
false => dp[i][j] = dp[i - 1][j].max(dp[i - 1][j - weight[i]] + value[i]),
|
||||
}
|
||||
for (int i = 1; i < n; i++) {
|
||||
for (int j = 0; j <= bagweight; j++) {
|
||||
if (j < weight[i]) {
|
||||
dp[i][j] = dp[i - 1][j];
|
||||
} else {
|
||||
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
|
||||
}
|
||||
}
|
||||
dp[weight.len() - 1][bag_size]
|
||||
}
|
||||
|
||||
printf("%d\n", dp[n - 1][bagweight]);
|
||||
|
||||
for (int i = 0; i < n; ++i) {
|
||||
free(dp[i]);
|
||||
}
|
||||
free(dp);
|
||||
free(weight);
|
||||
free(value);
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
#[test]
|
||||
fn test_wei_bag_problem1() {
|
||||
println!(
|
||||
"{}",
|
||||
Solution::wei_bag_problem1(vec![1, 3, 4], vec![15, 20, 30], 4)
|
||||
);
|
||||
}
|
||||
```
|
||||
|
||||
|
||||
|
||||
<p align="center">
|
||||
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
|
||||
<img src="../pics/网站星球宣传海报.jpg" width="1000"/>
|
||||
|
||||
Reference in New Issue
Block a user