Update

problems/kamacoder/0094.城市间货物运输I-SPFA.md

@@ -158,16 +158,11 @@
 
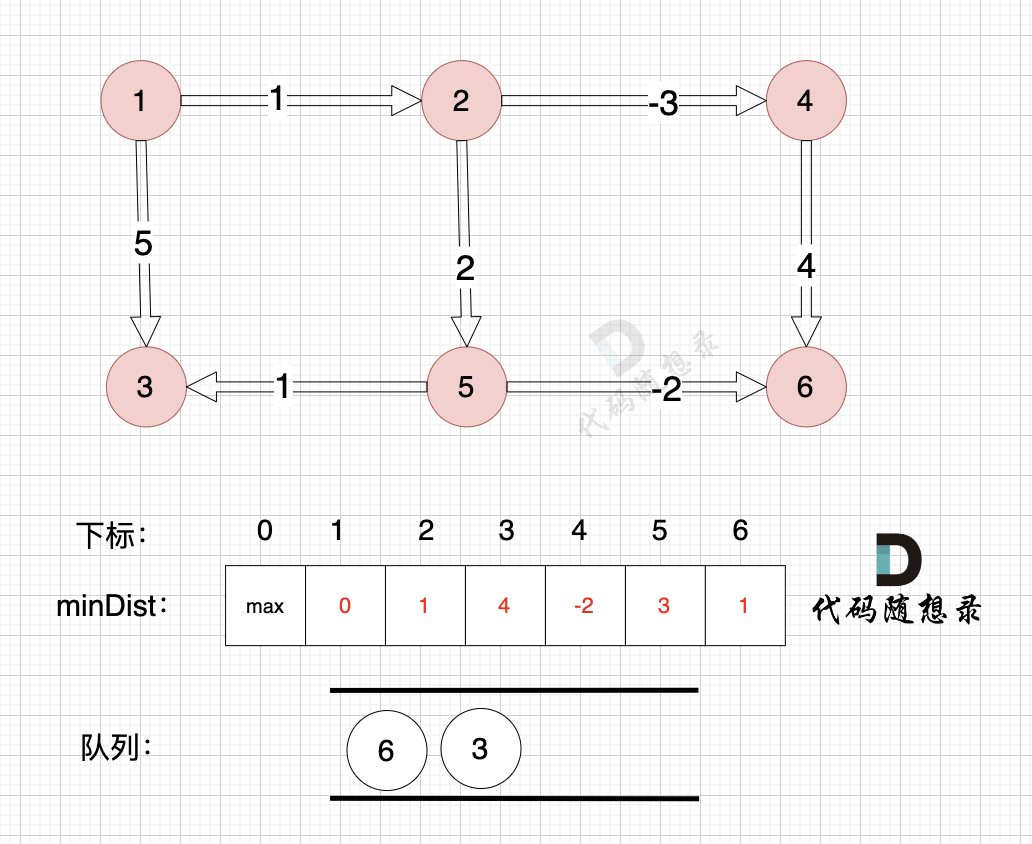
 边：节点5 -> 节点6，权值为-2 ，minDist[6] > minDist[5] + (-2) ，更新 minDist[6] = minDist[5] + (-2) = 3 - 2 = 1
 
-如图： 
+如图，将节点3加入队列，因为节点6已经在队列里，所以不用重复添加
 
-![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240412110509.png)
-
-
-
-因为节点3 和 节点6 都曾经加入过队列，不用重复加入，避免重复计算。   
-
-在代码中我们可以用一个数组 visited 来记录入过队列的元素，加入过队列的元素，不再重复入队列。
+![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240729161116.png)
 
+所以我们在加入队列的过程可以有一个优化，用visited数组记录已经加入队列的元素，已经在队列的元素不用重复加入
 
 -------------- 
 
@@ -175,11 +170,12 @@
 
 节点6作为终点，没有可以出发的边。 
 
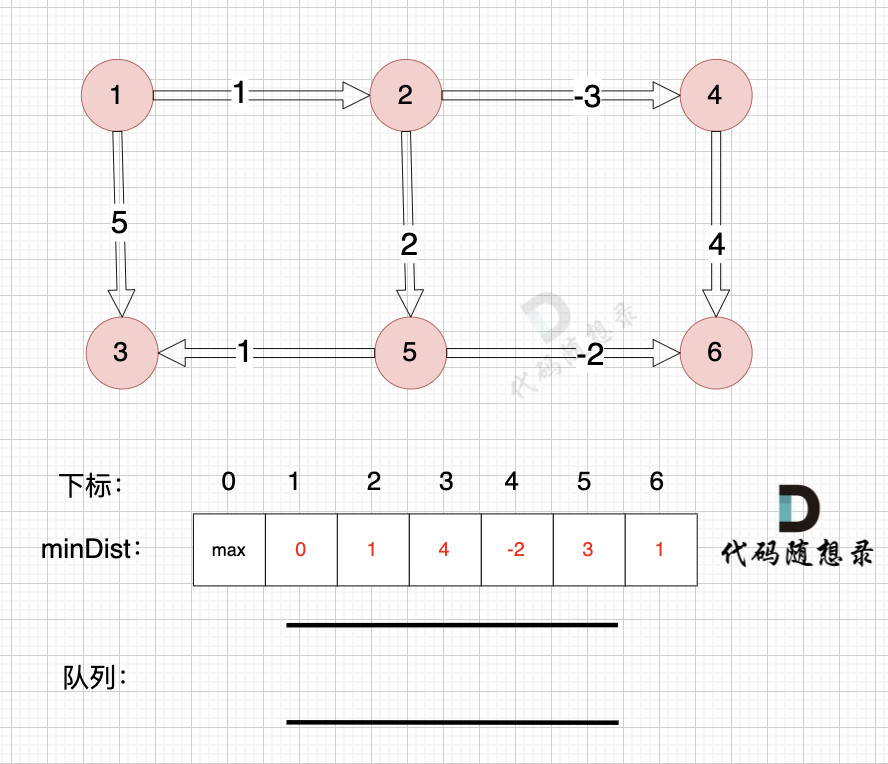
+同理从队列中取出节点3，也没有可以出发的边
+
 所以直接从队列中取出，如图： 
 
 ![](https://code-thinking-1253855093.file.myqcloud.com/pics/20240411115424.png) 
 
-
 ----------
 
 这样我们就完成了基于队列优化的bellman_ford的算法模拟过程。 
@@ -190,12 +186,12 @@
 
 在上面模拟过程中，我们每次都要知道 一个节点作为出发点连接了哪些节点。 
 
-如果想方便知道这些数据，就需要使用邻接表来存储这个图，如果对于邻接表不了解的话，可以看 [kama0047.参会dijkstra堆](./kama0047.参会dijkstra堆.md) 中 图的存储 部分。 
+如果想方便知道这些数据，就需要使用邻接表来存储这个图，如果对于邻接表不了解的话，可以看 [kama0047.参会dijkstra堆](./0047.参会dijkstra堆.md) 中 图的存储 部分。 
 
 
 整体代码如下：
 
-```CPP
+```
 #include <iostream>
 #include <vector>
 #include <queue>
@@ -215,7 +211,9 @@ int main() {
     int n, m, p1, p2, val;
     cin >> n >> m;
 
-    vector<list<Edge>> grid(n + 1); // 邻接表
+    vector<list<Edge>> grid(n + 1); 
+
+    vector<bool> isInQueue(n + 1); // 加入优化，已经在队里里的元素不用重复添加
 
     // 将所有边保存起来
     for(int i = 0; i < m; i++){
@@ -230,24 +228,26 @@ int main() {
     minDist[start] = 0;
 
     queue<int> que;
-    que.push(start); // 队列里放入起点
+    que.push(start); 
 
     while (!que.empty()) {
 
         int node = que.front(); que.pop();
-
+        isInQueue[node] = false; // 从队列里取出的时候，要取消标记
         for (Edge edge : grid[node]) {
             int from = node;
             int to = edge.to;
             int value = edge.val;
             if (minDist[to] > minDist[from] + value) { // 开始松弛
-                minDist[to] = minDist[from] + value;
-                que.push(to);
+                minDist[to] = minDist[from] + value; 
+                if (isInQueue[to] == false) { // 已经在队列里的元素不用重复添加
+                    que.push(to);
+                    isInQueue[to] = true;
+                }
             }
         }
 
     }
-
     if (minDist[end] == INT_MAX) cout << "unconnected" << endl; // 不能到达终点
     else cout << minDist[end] << endl; // 到达终点最短路径
 }