mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2026-02-03 02:43:26 +08:00
Merge branch 'master' of github.com:youngyangyang04/leetcode-master
This commit is contained in:
@@ -869,6 +869,65 @@ if __name__ == "__main__":
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
function dijkstra(grid, start, end) {
|
||||
const visited = Array.from({length: end + 1}, () => false)
|
||||
const minDist = Array.from({length: end + 1}, () => Number.MAX_VALUE)
|
||||
minDist[start] = 0
|
||||
|
||||
for (let i = 1 ; i < end + 1 ; i++) {
|
||||
let cur = -1
|
||||
let tempMinDist = Number.MAX_VALUE
|
||||
// 1. 找尋與起始點距離最近且未被訪的節點
|
||||
for (let j = 1 ; j < end + 1 ; j++) {
|
||||
if (!visited[j] && minDist[j] < tempMinDist) {
|
||||
cur = j
|
||||
tempMinDist = minDist[j]
|
||||
}
|
||||
}
|
||||
if (cur === -1) break;
|
||||
|
||||
// 2. 更新節點狀態為已拜訪
|
||||
visited[cur] = true
|
||||
|
||||
// 3. 更新未拜訪節點與起始點的最短距離
|
||||
for (let j = 1 ; j < end + 1 ; j++) {
|
||||
if(!visited[j] && grid[cur][j] != Number.MAX_VALUE
|
||||
&& grid[cur][j] + minDist[cur] < minDist[j]
|
||||
) {
|
||||
minDist[j] = grid[cur][j] + minDist[cur]
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
return minDist[end] === Number.MAX_VALUE ? -1 : minDist[end]
|
||||
}
|
||||
|
||||
|
||||
async function main() {
|
||||
// 輸入
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const [n, m] = (await readline()).split(" ").map(Number)
|
||||
const grid = Array.from({length: n + 1},
|
||||
() => Array.from({length:n + 1}, () => Number.MAX_VALUE))
|
||||
for (let i = 0 ; i < m ; i++) {
|
||||
const [s, e, w] = (await readline()).split(" ").map(Number)
|
||||
grid[s][e] = w
|
||||
}
|
||||
|
||||
// dijkstra
|
||||
const result = dijkstra(grid, 1, n)
|
||||
|
||||
// 輸出
|
||||
console.log(result)
|
||||
}
|
||||
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@@ -9,17 +9,17 @@
|
||||
|
||||
在世界的某个区域,有一些分散的神秘岛屿,每个岛屿上都有一种珍稀的资源或者宝藏。国王打算在这些岛屿上建公路,方便运输。
|
||||
|
||||
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将 所有岛屿联通起来。
|
||||
不同岛屿之间,路途距离不同,国王希望你可以规划建公路的方案,如何可以以最短的总公路距离将所有岛屿联通起来。
|
||||
|
||||
给定一张地图,其中包括了所有的岛屿,以及它们之间的距离。以最小化公路建设长度,确保可以链接到所有岛屿。
|
||||
|
||||
输入描述:
|
||||
|
||||
第一行包含两个整数V 和 E,V代表顶点数,E代表边数 。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
|
||||
第一行包含两个整数V和E,V代表顶点数,E代表边数。顶点编号是从1到V。例如:V=2,一个有两个顶点,分别是1和2。
|
||||
|
||||
接下来共有 E 行,每行三个整数 v1,v2 和 val,v1 和 v2 为边的起点和终点,val代表边的权值。
|
||||
接下来共有E行,每行三个整数v1,v2和val,v1和v2为边的起点和终点,val代表边的权值。
|
||||
|
||||
输出描述:
|
||||
输出描述:
|
||||
|
||||
输出联通所有岛屿的最小路径总距离
|
||||
|
||||
@@ -38,65 +38,65 @@
|
||||
5 6 2
|
||||
5 7 1
|
||||
6 7 1
|
||||
```
|
||||
```
|
||||
|
||||
输出示例:
|
||||
输出示例:
|
||||
|
||||
6
|
||||
|
||||
|
||||
## 解题思路
|
||||
## 解题思路
|
||||
|
||||
本题是最小生成树的模板题,那么我们来讲一讲最小生成树。
|
||||
本题是最小生成树的模板题,那么我们来讲一讲最小生成树。
|
||||
|
||||
最小生成树 可以使用 prim算法 也可以使用 kruskal算法计算出来。
|
||||
最小生成树可以使用prim算法也可以使用kruskal算法计算出来。
|
||||
|
||||
本篇我们先讲解 prim算法。
|
||||
本篇我们先讲解prim算法。
|
||||
|
||||
最小生成树是所有节点的最小连通子图, 即:以最小的成本(边的权值)将图中所有节点链接到一起。
|
||||
最小生成树是所有节点的最小连通子图,即:以最小的成本(边的权值)将图中所有节点链接到一起。
|
||||
|
||||
图中有n个节点,那么一定可以用 n - 1 条边将所有节点连接到一起。
|
||||
图中有n个节点,那么一定可以用n-1条边将所有节点连接到一起。
|
||||
|
||||
那么如何选择 这 n-1 条边 就是 最小生成树算法的任务所在。
|
||||
那么如何选择这n-1条边就是最小生成树算法的任务所在。
|
||||
|
||||
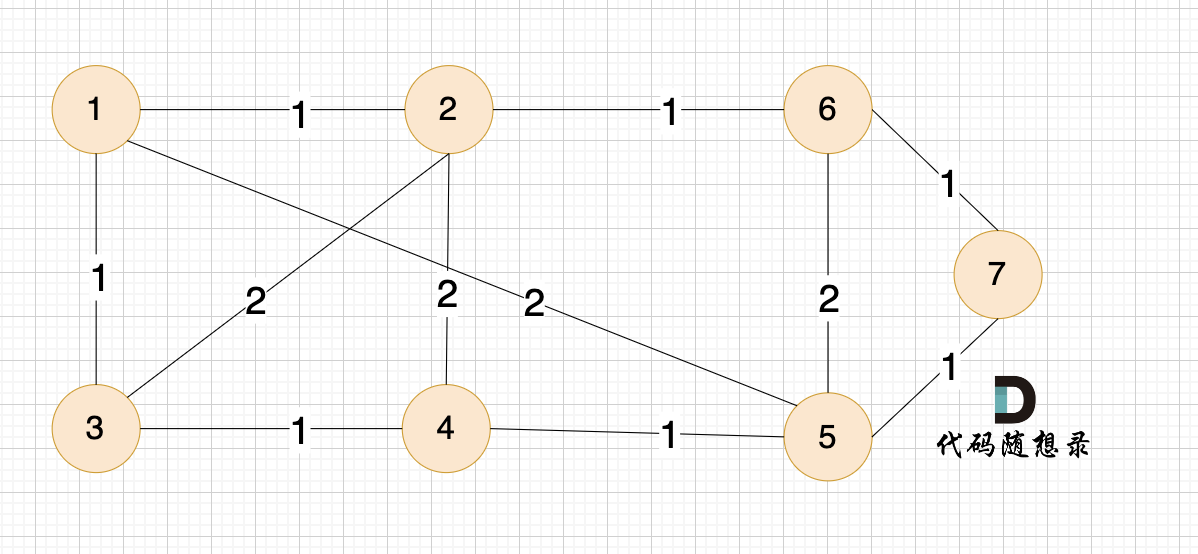
例如本题示例中的无向有权图为:
|
||||
例如本题示例中的无向有权图为:
|
||||
|
||||
|
||||
|
||||
那么在这个图中,如何选取 n-1 条边 使得 图中所有节点连接到一起,并且边的权值和最小呢?
|
||||
那么在这个图中,如何选取n-1条边使得图中所有节点连接到一起,并且边的权值和最小呢?
|
||||
|
||||
(图中为n为7,即7个节点,那么只需要 n-1 即 6条边就可以讲所有顶点连接到一起)
|
||||
(图中为n为7,即7个节点,那么只需要n-1即6条边就可以讲所有顶点连接到一起)
|
||||
|
||||
prim算法 是从节点的角度 采用贪心的策略 每次寻找距离 最小生成树最近的节点 并加入到最小生成树中。
|
||||
prim算法是从节点的角度采用贪心的策略每次寻找距离最小生成树最近的节点并加入到最小生成树中。
|
||||
|
||||
prim算法核心就是三步,我称为**prim三部曲**,大家一定要熟悉这三步,代码相对会好些很多:
|
||||
prim算法核心就是三步,我称为**prim三部曲**,大家一定要熟悉这三步,代码相对会好些很多:
|
||||
|
||||
1. 第一步,选距离生成树最近节点
|
||||
2. 第二步,最近节点加入生成树
|
||||
2. 第二步,最近节点加入生成树
|
||||
3. 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
现在录友们会对这三步很陌生,不知道这是干啥的,没关系,下面将会画图举例来带大家把这**prim三部曲**理解到位。
|
||||
现在录友们会对这三步很陌生,不知道这是干啥的,没关系,下面将会画图举例来带大家把这**prim三部曲**理解到位。
|
||||
|
||||
在prim算法中,有一个数组特别重要,这里我起名为:minDist。
|
||||
|
||||
刚刚我有讲过 “每次寻找距离 最小生成树最近的节点 并加入到最小生成树中”,那么如何寻找距离最小生成树最近的节点呢?
|
||||
刚刚我有讲过“每次寻找距离最小生成树最近的节点并加入到最小生成树中”,那么如何寻找距离最小生成树最近的节点呢?
|
||||
|
||||
这就用到了 minDist 数组, 它用来作什么呢?
|
||||
这就用到了minDist数组,它用来作什么呢?
|
||||
|
||||
**minDist数组 用来记录 每一个节点距离最小生成树的最近距离**。 理解这一点非常重要,这也是 prim算法最核心要点所在,很多录友看不懂prim算法的代码,都是因为没有理解透 这个数组的含义。
|
||||
**minDist数组用来记录每一个节点距离最小生成树的最近距离**。理解这一点非常重要,这也是prim算法最核心要点所在,很多录友看不懂prim算法的代码,都是因为没有理解透这个数组的含义。
|
||||
|
||||
接下来,我们来通过一步一步画图,来带大家巩固 **prim三部曲** 以及 minDist数组 的作用。
|
||||
接下来,我们来通过一步一步画图,来带大家巩固**prim三部曲**以及minDist数组的作用。
|
||||
|
||||
(**示例中节点编号是从1开始,所以为了让大家看的不晕,minDist数组下标我也从 1 开始计数,下标0 就不使用了,这样 下标和节点标号就可以对应上了,避免大家搞混**)
|
||||
(**示例中节点编号是从1开始,所以为了让大家看的不晕,minDist数组下标我也从1开始计数,下标0就不使用了,这样下标和节点标号就可以对应上了,避免大家搞混**)
|
||||
|
||||
|
||||
### 1 初始状态
|
||||
### 1 初始状态
|
||||
|
||||
minDist 数组 里的数值初始化为 最大数,因为本题 节点距离不会超过 10000,所以 初始化最大数为 10001就可以。
|
||||
minDist数组里的数值初始化为最大数,因为本题节点距离不会超过10000,所以初始化最大数为10001就可以。
|
||||
|
||||
相信这里录友就要问了,为什么这么做?
|
||||
相信这里录友就要问了,为什么这么做?
|
||||
|
||||
现在 还没有最小生成树,默认每个节点距离最小生成树是最大的,这样后面我们在比较的时候,发现更近的距离,才能更新到 minDist 数组上。
|
||||
现在还没有最小生成树,默认每个节点距离最小生成树是最大的,这样后面我们在比较的时候,发现更近的距离,才能更新到minDist数组上。
|
||||
|
||||
如图:
|
||||
|
||||
@@ -108,125 +108,125 @@ minDist 数组 里的数值初始化为 最大数,因为本题 节点距离不
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好(因为每一个节点一定会在最小生成树里,所以随便选一个就好),那我们选择节点1 (符合遍历数组的习惯,第一个遍历的也是节点1)
|
||||
选择距离最小生成树最近的节点,加入到最小生成树,刚开始还没有最小生成树,所以随便选一个节点加入就好(因为每一个节点一定会在最小生成树里,所以随便选一个就好),那我们选择节点1(符合遍历数组的习惯,第一个遍历的也是节点1)
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
此时 节点1 已经算最小生成树的节点。
|
||||
此时节点1已经算最小生成树的节点。
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
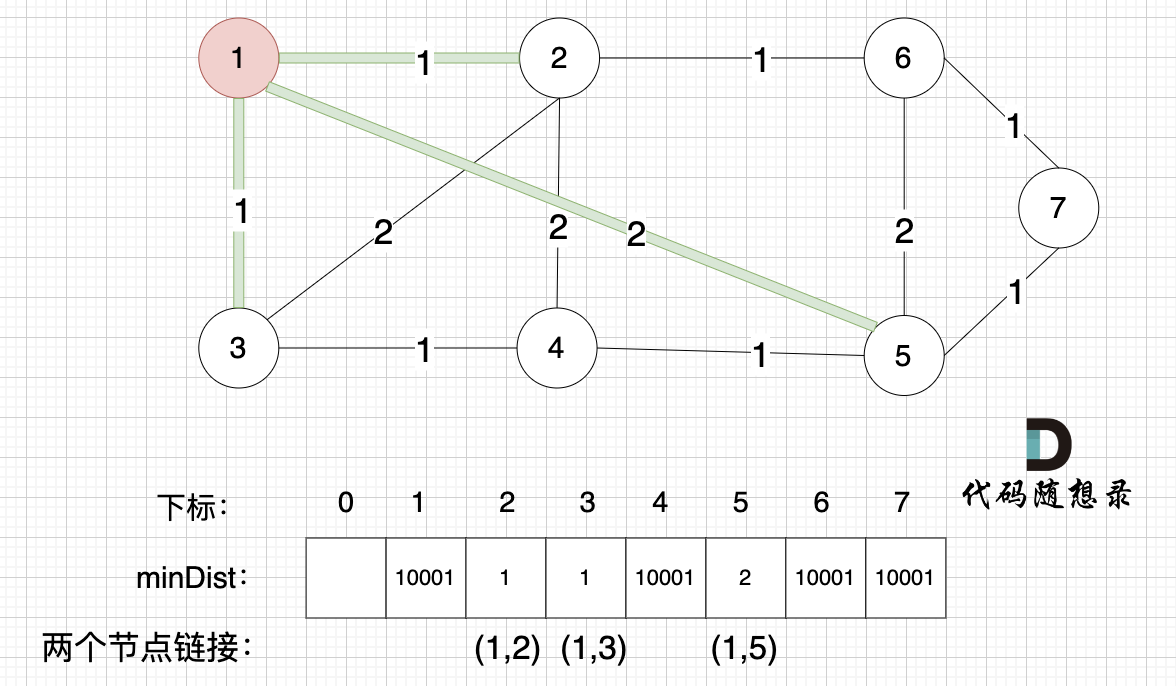
接下来,我们要更新所有节点距离最小生成树的距离,如图:
|
||||
接下来,我们要更新所有节点距离最小生成树的距离,如图:
|
||||
|
||||
|
||||
|
||||
|
||||
注意下标0,我们就不管它了,下标 1 与节点 1 对应,这样可以避免大家把节点搞混。
|
||||
注意下标0,我们就不管它了,下标1与节点1对应,这样可以避免大家把节点搞混。
|
||||
|
||||
此时所有非生成树的节点距离 最小生成树(节点1)的距离都已经跟新了 。
|
||||
此时所有非生成树的节点距离最小生成树(节点1)的距离都已经跟新了。
|
||||
|
||||
* 节点2 与 节点1 的距离为1,比原先的 距离值10001小,所以更新minDist[2]。
|
||||
* 节点3 和 节点1 的距离为1,比原先的 距离值10001小,所以更新minDist[3]。
|
||||
* 节点5 和 节点1 的距离为2,比原先的 距离值10001小,所以更新minDist[5]。
|
||||
* 节点2与节点1的距离为1,比原先的距离值10001小,所以更新minDist[2]。
|
||||
* 节点3和节点1的距离为1,比原先的距离值10001小,所以更新minDist[3]。
|
||||
* 节点5和节点1的距离为2,比原先的距离值10001小,所以更新minDist[5]。
|
||||
|
||||
**注意图中我标记了 minDist数组里更新的权值**,是哪两个节点之间的权值,例如 minDist[2] =1 ,这个 1 是 节点1 与 节点2 之间的连线,清楚这一点对最后我们记录 最小生成树的权值总和很重要。
|
||||
**注意图中我标记了minDist数组里更新的权值**,是哪两个节点之间的权值,例如minDist[2]=1,这个1是节点1与节点2之间的连线,清楚这一点对最后我们记录最小生成树的权值总和很重要。
|
||||
|
||||
(我在后面依然会不断重复 prim三部曲,可能基础好的录友会感觉有点啰嗦,但也是让大家感觉这三部曲求解的过程)
|
||||
(我在后面依然会不断重复prim三部曲,可能基础好的录友会感觉有点啰嗦,但也是让大家感觉这三部曲求解的过程)
|
||||
|
||||
### 3
|
||||
### 3
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
选取一个距离 最小生成树(节点1) 最近的非生成树里的节点,节点2,3,5 距离 最小生成树(节点1) 最近,选节点 2(其实选 节点3或者节点2都可以,距离一样的)加入最小生成树。
|
||||
选取一个距离最小生成树(节点1)最近的非生成树里的节点,节点2,3,5距离最小生成树(节点1)最近,选节点2(其实选节点3或者节点2都可以,距离一样的)加入最小生成树。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
此时 节点1 和 节点2,已经算最小生成树的节点。
|
||||
此时节点1和节点2,已经算最小生成树的节点。
|
||||
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
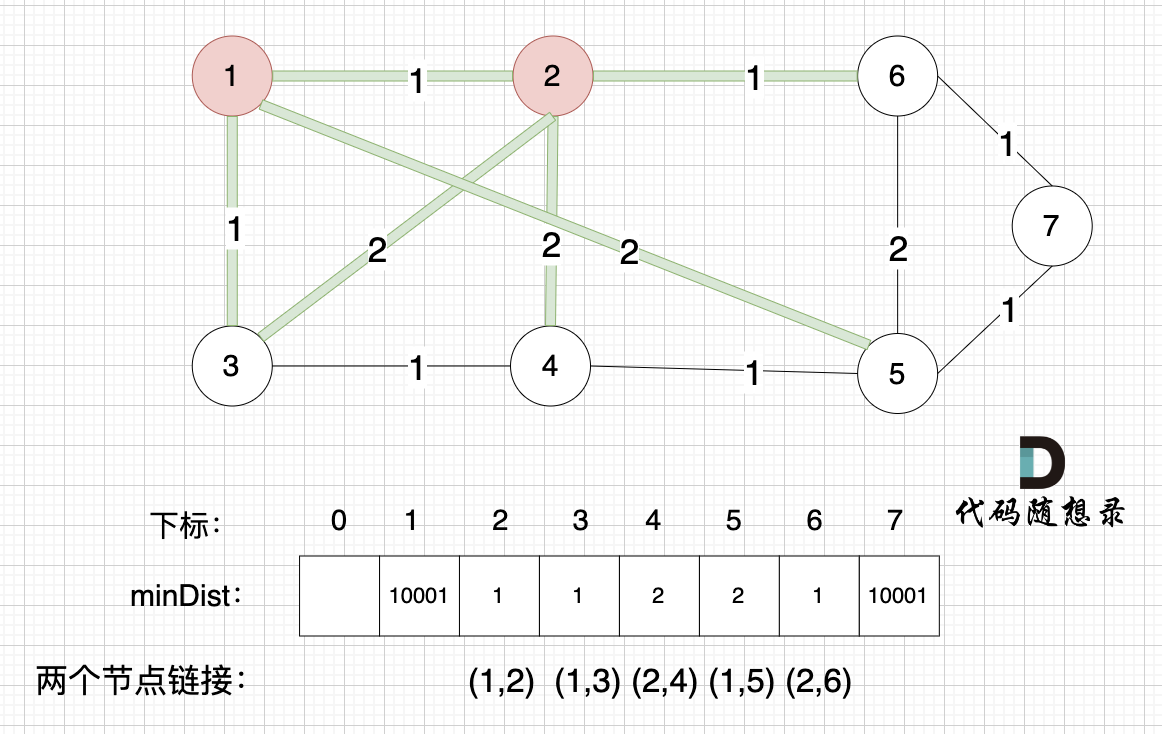
接下来,我们要更新节点距离最小生成树的距离,如图:
|
||||
接下来,我们要更新节点距离最小生成树的距离,如图:
|
||||
|
||||
|
||||

|
||||
|
||||
此时所有非生成树的节点距离 最小生成树(节点1、节点2)的距离都已经跟新了 。
|
||||
此时所有非生成树的节点距离最小生成树(节点1、节点2)的距离都已经跟新了。
|
||||
|
||||
* 节点3 和 节点2 的距离为2,和原先的距离值1 小,所以不用更新。
|
||||
* 节点4 和 节点2 的距离为2,比原先的距离值10001小,所以更新minDist[4]。
|
||||
* 节点5 和 节点2 的距离为10001(不连接),所以不用更新。
|
||||
* 节点6 和 节点2 的距离为1,比原先的距离值10001小,所以更新minDist[6]。
|
||||
* 节点3和节点2的距离为2,和原先的距离值1小,所以不用更新。
|
||||
* 节点4和节点2的距离为2,比原先的距离值10001小,所以更新minDist[4]。
|
||||
* 节点5和节点2的距离为10001(不连接),所以不用更新。
|
||||
* 节点6和节点2的距离为1,比原先的距离值10001小,所以更新minDist[6]。
|
||||
|
||||
### 4
|
||||
### 4
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
选择一个距离 最小生成树(节点1、节点2) 最近的非生成树里的节点,节点3,6 距离 最小生成树(节点1、节点2) 最近,选节点3 (选节点6也可以,距离一样)加入最小生成树。
|
||||
选择一个距离最小生成树(节点1、节点2)最近的非生成树里的节点,节点3,6距离最小生成树(节点1、节点2)最近,选节点3(选节点6也可以,距离一样)加入最小生成树。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
此时 节点1 、节点2 、节点3 算是最小生成树的节点。
|
||||
此时节点1、节点2、节点3算是最小生成树的节点。
|
||||
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
接下来更新节点距离最小生成树的距离,如图:
|
||||
接下来更新节点距离最小生成树的距离,如图:
|
||||
|
||||

|
||||

|
||||
|
||||
所有非生成树的节点距离 最小生成树(节点1、节点2、节点3 )的距离都已经跟新了 。
|
||||
所有非生成树的节点距离最小生成树(节点1、节点2、节点3)的距离都已经跟新了。
|
||||
|
||||
* 节点 4 和 节点 3的距离为 1,和原先的距离值 2 小,所以更新minDist[4]为1。
|
||||
* 节点4和节点3的距离为1,和原先的距离值2小,所以更新minDist[4]为1。
|
||||
|
||||
上面为什么我们只比较 节点4 和 节点3 的距离呢?
|
||||
上面为什么我们只比较节点4和节点3的距离呢?
|
||||
|
||||
因为节点3加入 最小生成树后,非 生成树节点 只有 节点 4 和 节点3是链接的,所以需要重新更新一下 节点4距离最小生成树的距离,其他节点距离最小生成树的距离 都不变。
|
||||
因为节点3加入最小生成树后,非生成树节点只有节点4和节点3是链接的,所以需要重新更新一下节点4距离最小生成树的距离,其他节点距离最小生成树的距离都不变。
|
||||
|
||||
### 5
|
||||
### 5
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
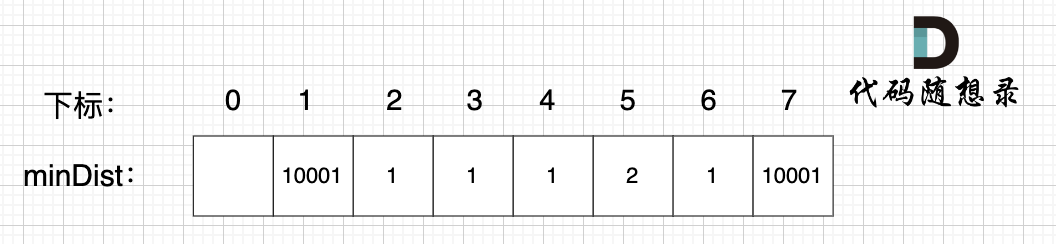
继续选择一个距离 最小生成树(节点1、节点2、节点3) 最近的非生成树里的节点,为了巩固大家对 minDist数组的理解,这里我再啰嗦一遍:
|
||||
继续选择一个距离最小生成树(节点1、节点2、节点3)最近的非生成树里的节点,为了巩固大家对minDist数组的理解,这里我再啰嗦一遍:
|
||||
|
||||
|
||||

|
||||
|
||||
**minDist数组 是记录了 所有非生成树节点距离生成树的最小距离**,所以 从数组里我们能看出来,非生成树节点 4 和 节点 6 距离 生成树最近。
|
||||
**minDist数组是记录了所有非生成树节点距离生成树的最小距离**,所以从数组里我们能看出来,非生成树节点4和节点6距离生成树最近。
|
||||
|
||||
|
||||
任选一个加入生成树,我们选 节点4(选节点6也行) 。
|
||||
任选一个加入生成树,我们选节点4(选节点6也行)。
|
||||
|
||||
**注意**,我们根据 minDist数组,选取距离 生成树 最近的节点 加入生成树,那么 **minDist数组里记录的其实也是 最小生成树的边的权值**(我在图中把权值对应的是哪两个节点也标记出来了)。
|
||||
**注意**,我们根据minDist数组,选取距离生成树最近的节点加入生成树,那么**minDist数组里记录的其实也是最小生成树的边的权值**(我在图中把权值对应的是哪两个节点也标记出来了)。
|
||||
|
||||
如果大家不理解,可以跟着我们下面的讲解,看 minDist数组的变化, minDist数组 里记录的权值对应的哪条边。
|
||||
如果大家不理解,可以跟着我们下面的讲解,看minDist数组的变化,minDist数组里记录的权值对应的哪条边。
|
||||
|
||||
理解这一点很重要,因为 最后我们要求 最小生成树里所有边的权值和。
|
||||
理解这一点很重要,因为最后我们要求最小生成树里所有边的权值和。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
此时 节点1、节点2、节点3、节点4 算是 最小生成树的节点。
|
||||
此时节点1、节点2、节点3、节点4算是最小生成树的节点。
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
接下来更新节点距离最小生成树的距离,如图:
|
||||
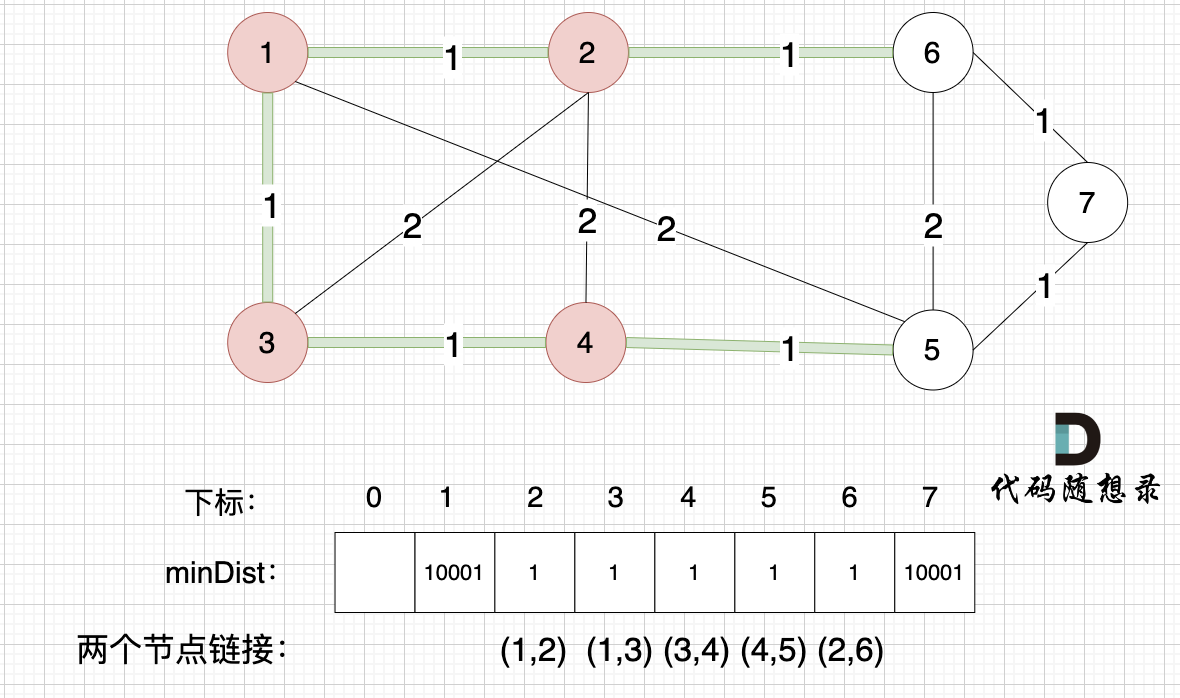
接下来更新节点距离最小生成树的距离,如图:
|
||||
|
||||
|
||||

|
||||
|
||||
minDist数组已经更新了 所有非生成树的节点距离 最小生成树(节点1、节点2、节点3、节点4 )的距离 。
|
||||
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4)的距离。
|
||||
|
||||
* 节点 5 和 节点 4的距离为 1,和原先的距离值 2 小,所以更新minDist[5]为1。
|
||||
* 节点5和节点4的距离为1,和原先的距离值2小,所以更新minDist[5]为1。
|
||||
|
||||
### 6
|
||||
### 6
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
继续选距离 最小生成树(节点1、节点2、节点3、节点4 )最近的非生成树里的节点,只有 节点 5 和 节点6。
|
||||
继续选距离最小生成树(节点1、节点2、节点3、节点4)最近的非生成树里的节点,只有节点5和节点6。
|
||||
|
||||
|
||||
选节点5 (选节点6也可以)加入 生成树。
|
||||
选节点5(选节点6也可以)加入生成树。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
节点1、节点2、节点3、节点4、节点5 算是 最小生成树的节点。
|
||||
节点1、节点2、节点3、节点4、节点5算是最小生成树的节点。
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
@@ -234,44 +234,44 @@ minDist数组已经更新了 所有非生成树的节点距离 最小生成树
|
||||
|
||||
|
||||
|
||||
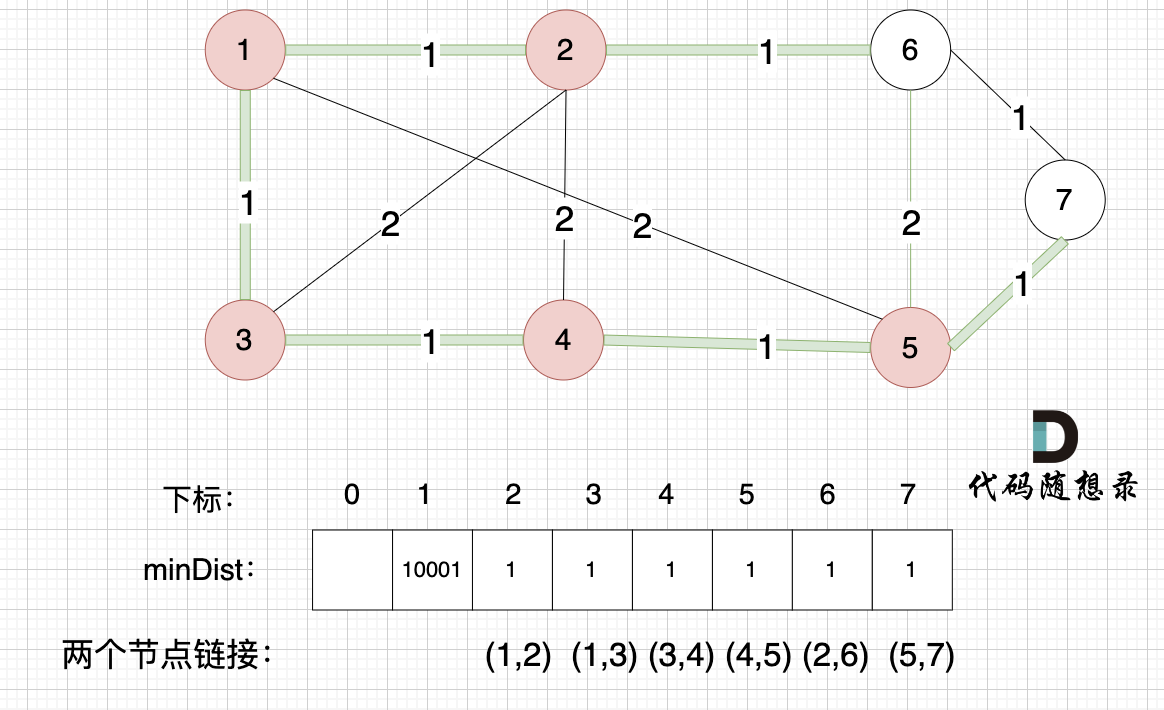
minDist数组已经更新了 所有非生成树的节点距离 最小生成树(节点1、节点2、节点3、节点4 、节点5)的距离 。
|
||||
minDist数组已经更新了所有非生成树的节点距离最小生成树(节点1、节点2、节点3、节点4、节点5)的距离。
|
||||
|
||||
* 节点 6 和 节点 5 距离为 2,比原先的距离值 1 大,所以不更新
|
||||
* 节点 7 和 节点 5 距离为 1,比原先的距离值 10001小,更新 minDist[7]
|
||||
* 节点6和节点5距离为2,比原先的距离值1大,所以不更新
|
||||
* 节点7和节点5距离为1,比原先的距离值10001小,更新minDist[7]
|
||||
|
||||
### 7
|
||||
### 7
|
||||
|
||||
1、prim三部曲,第一步:选距离生成树最近节点
|
||||
|
||||
继续选距离 最小生成树(节点1、节点2、节点3、节点4 、节点5)最近的非生成树里的节点,只有 节点 6 和 节点7。
|
||||
继续选距离最小生成树(节点1、节点2、节点3、节点4、节点5)最近的非生成树里的节点,只有节点6和节点7。
|
||||
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
2、prim三部曲,第二步:最近节点加入生成树
|
||||
|
||||
选节点6 (选节点7也行,距离一样的)加入生成树。
|
||||
选节点6(选节点7也行,距离一样的)加入生成树。
|
||||
|
||||
3、prim三部曲,第三步:更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
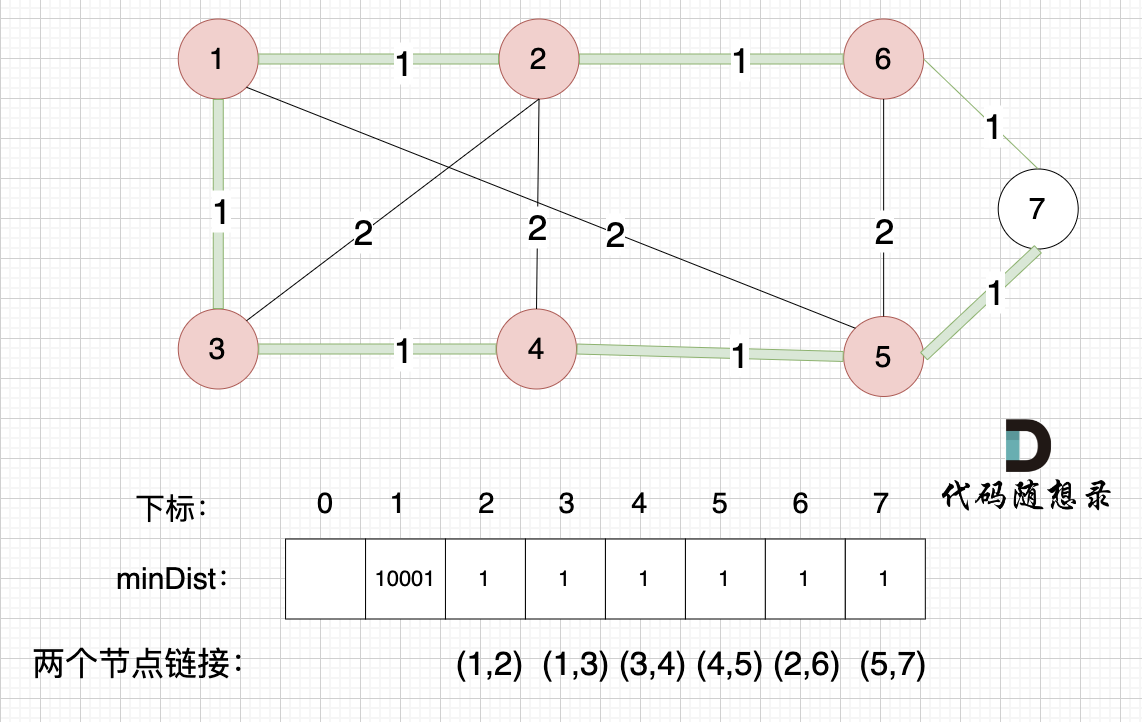
节点1、节点2、节点3、节点4、节点5、节点6 算是 最小生成树的节点 ,接下来更新节点距离最小生成树的距离,如图:
|
||||
节点1、节点2、节点3、节点4、节点5、节点6算是最小生成树的节点,接下来更新节点距离最小生成树的距离,如图:
|
||||
|
||||
|
||||
|
||||
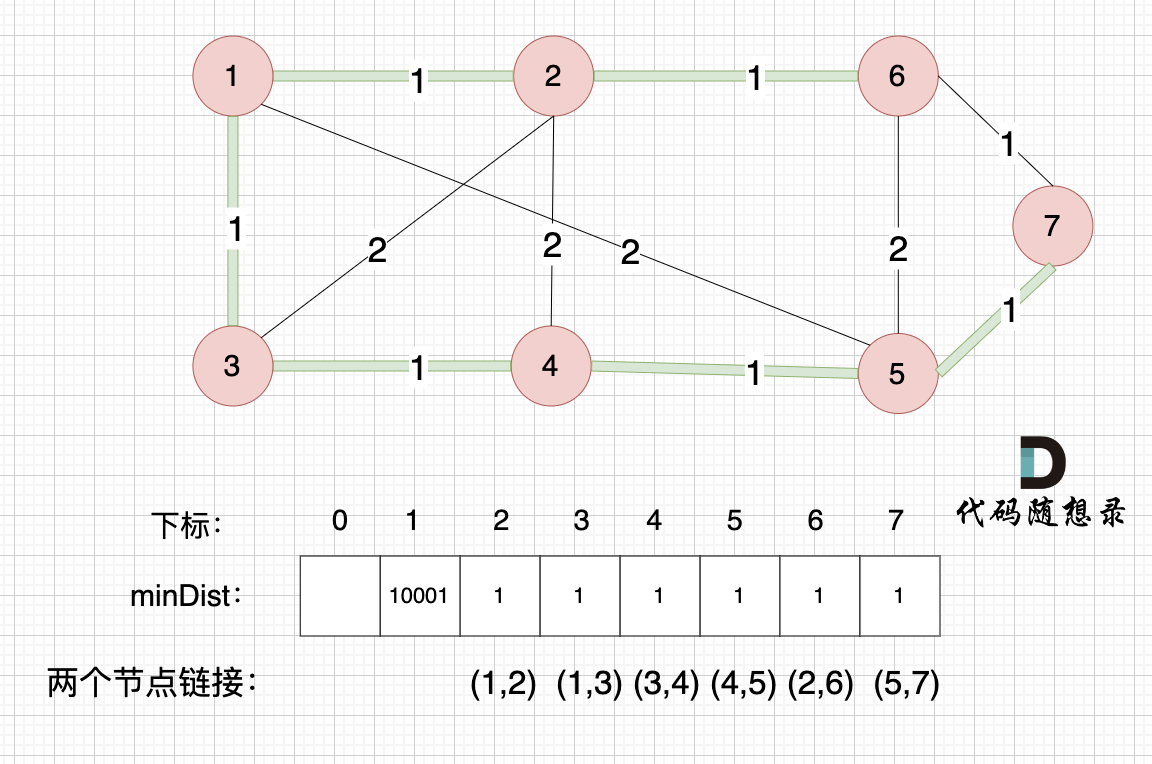
这里就不在重复描述了,大家类推,最后,节点7加入生成树,如图:
|
||||
这里就不在重复描述了,大家类推,最后,节点7加入生成树,如图:
|
||||
|
||||
|
||||

|
||||
|
||||
### 最后
|
||||
### 最后
|
||||
|
||||
最后我们就生成了一个 最小生成树, 绿色的边将所有节点链接到一起,并且 保证权值是最小的,因为我们在更新 minDist 数组的时候,都是选距离 最小生成树最近的点 加入到树中。
|
||||
最后我们就生成了一个最小生成树,绿色的边将所有节点链接到一起,并且保证权值是最小的,因为我们在更新minDist数组的时候,都是选距离最小生成树最近的点加入到树中。
|
||||
|
||||
讲解上面的模拟过程的时候,我已经强调多次 minDist数组 是记录了 所有非生成树节点距离生成树的最小距离。
|
||||
讲解上面的模拟过程的时候,我已经强调多次minDist数组是记录了所有非生成树节点距离生成树的最小距离。
|
||||
|
||||
最后,minDist数组 也就是记录的是最小生成树所有边的权值。
|
||||
最后,minDist数组也就是记录的是最小生成树所有边的权值。
|
||||
|
||||
我在图中,特别把 每条边的权值对应的是哪两个节点 标记出来(例如minDist[7] = 1,对应的是节点5 和 节点7之间的边,而不是 节点6 和 节点7),为了就是让大家清楚, minDist里的每一个值 对应的是哪条边。
|
||||
我在图中,特别把每条边的权值对应的是哪两个节点标记出来(例如minDist[7]=1,对应的是节点5和节点7之间的边,而不是节点6和节点7),为了就是让大家清楚,minDist里的每一个值对应的是哪条边。
|
||||
|
||||
那么我们要求最小生成树里边的权值总和 就是 把 最后的 minDist 数组 累加一起。
|
||||
那么我们要求最小生成树里边的权值总和就是把最后的minDist数组累加一起。
|
||||
|
||||
以下代码,我对 prim三部曲,做了重点注释,大家根据这三步,就可以 透彻理解prim。
|
||||
以下代码,我对prim三部曲,做了重点注释,大家根据这三步,就可以透彻理解prim。
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
@@ -338,52 +338,52 @@ int main() {
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
```
|
||||
|
||||
时间复杂度为 O(n^2),其中 n 为节点数量。
|
||||
时间复杂度为O(n^2),其中n为节点数量。
|
||||
|
||||
## 拓展
|
||||
|
||||
上面讲解的是记录了最小生成树 所有边的权值,如果让打印出来 最小生成树的每条边呢? 或者说 要把这个最小生成树画出来呢?
|
||||
上面讲解的是记录了最小生成树所有边的权值,如果让打印出来最小生成树的每条边呢?或者说要把这个最小生成树画出来呢?
|
||||
|
||||
|
||||
此时我们就需要把 最小生成树里每一条边记录下来。
|
||||
此时我们就需要把最小生成树里每一条边记录下来。
|
||||
|
||||
此时有两个问题:
|
||||
此时有两个问题:
|
||||
|
||||
* 1、用什么结构来记录
|
||||
* 2、如何记录
|
||||
* 1、用什么结构来记录
|
||||
* 2、如何记录
|
||||
|
||||
如果记录边,其实就是记录两个节点就可以,两个节点连成一条边。
|
||||
如果记录边,其实就是记录两个节点就可以,两个节点连成一条边。
|
||||
|
||||
如何记录两个节点呢?
|
||||
|
||||
我们使用一维数组就可以记录。 parent[节点编号] = 节点编号, 这样就把一条边记录下来了。(当然如果节点编号非常大,可以考虑使用map)
|
||||
我们使用一维数组就可以记录。parent[节点编号] = 节点编号,这样就把一条边记录下来了。(当然如果节点编号非常大,可以考虑使用map)
|
||||
|
||||
使用一维数组记录是有向边,不过我们这里不需要记录方向,所以只关注两条边是连接的就行。
|
||||
使用一维数组记录是有向边,不过我们这里不需要记录方向,所以只关注两条边是连接的就行。
|
||||
|
||||
parent数组初始化代码:
|
||||
parent数组初始化代码:
|
||||
|
||||
```CPP
|
||||
vector<int> parent(v + 1, -1);
|
||||
```
|
||||
|
||||
接下来就是第二个问题,如何记录?
|
||||
接下来就是第二个问题,如何记录?
|
||||
|
||||
我们再来回顾一下 prim三部曲,
|
||||
我们再来回顾一下prim三部曲,
|
||||
|
||||
1. 第一步,选距离生成树最近节点
|
||||
2. 第二步,最近节点加入生成树
|
||||
2. 第二步,最近节点加入生成树
|
||||
3. 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
大家先思考一下,我们是在第几步,可以记录 最小生成树的边呢?
|
||||
大家先思考一下,我们是在第几步,可以记录最小生成树的边呢?
|
||||
|
||||
在本面上半篇 我们讲解过:“我们根据 minDist数组,选组距离 生成树 最近的节点 加入生成树,那么 **minDist数组里记录的其实也是 最小生成树的边的权值**。”
|
||||
在本面上半篇我们讲解过:“我们根据minDist数组,选组距离生成树最近的节点加入生成树,那么**minDist数组里记录的其实也是最小生成树的边的权值**。”
|
||||
|
||||
既然 minDist数组 记录了 最小生成树的边,是不是就是在更新 minDist数组 的时候,去更新parent数组来记录一下对应的边呢。
|
||||
既然minDist数组记录了最小生成树的边,是不是就是在更新minDist数组的时候,去更新parent数组来记录一下对应的边呢。
|
||||
|
||||
|
||||
所以 在 prim三部曲中的第三步,更新 parent数组,代码如下:
|
||||
所以在prim三部曲中的第三步,更新parent数组,代码如下:
|
||||
|
||||
```CPP
|
||||
for (int j = 1; j <= v; j++) {
|
||||
@@ -394,23 +394,23 @@ for (int j = 1; j <= v; j++) {
|
||||
}
|
||||
```
|
||||
|
||||
代码中注释中,我强调了 数组指向的顺序很重要。 因为不少录友在这里会写成这样: `parent[cur] = j` 。
|
||||
代码中注释中,我强调了数组指向的顺序很重要。因为不少录友在这里会写成这样: `parent[cur] = j` 。
|
||||
|
||||
这里估计大家会疑惑了,parent[节点编号A] = 节点编号B, 就表示A 和 B 相连,我们这里就不用在意方向,代码中 为什么 只能 `parent[j] = cur` 而不能 `parent[cur] = j` 这么写呢?
|
||||
这里估计大家会疑惑了,parent[节点编号A] = 节点编号B,就表示A和B相连,我们这里就不用在意方向,代码中为什么只能 `parent[j] = cur` 而不能 `parent[cur] = j` 这么写呢?
|
||||
|
||||
如果写成 `parent[cur] = j`,在 for 循环中,有多个 j 满足要求, 那么 parent[cur] 就会被反复覆盖,因为 cur 是一个固定值。
|
||||
如果写成 `parent[cur] = j`,在for循环中,有多个j满足要求,那么 parent[cur] 就会被反复覆盖,因为cur是一个固定值。
|
||||
|
||||
举个例子,cur = 1, 在 for循环中,可能 就 j = 2, j = 3,j =4 都符合条件,那么本来应该记录 节点1 与 节点 2、节点3、节点4相连的。
|
||||
举个例子,cur=1,在for循环中,可能就j=2,j=3,j=4都符合条件,那么本来应该记录节点1与节点2、节点3、节点4相连的。
|
||||
|
||||
如果 `parent[cur] = j` 这么写,最后更新的逻辑是 parent[1] = 2, parent[1] = 3, parent[1] = 4, 最后只能记录 节点1 与节点 4 相连,其他相连情况都被覆盖了。
|
||||
如果 `parent[cur] = j` 这么写,最后更新的逻辑是 parent[1] = 2, parent[1] = 3, parent[1] = 4,最后只能记录节点1与节点4相连,其他相连情况都被覆盖了。
|
||||
|
||||
如果这么写 `parent[j] = cur`, 那就是 parent[2] = 1, parent[3] = 1, parent[4] = 1 ,这样 才能完整表示出 节点1 与 其他节点都是链接的,才没有被覆盖。
|
||||
如果这么写 `parent[j] = cur`,那就是 parent[2] = 1, parent[3] = 1, parent[4] = 1 ,这样才能完整表示出节点1与其他节点都是链接的,才没有被覆盖。
|
||||
|
||||
主要问题也是我们使用了一维数组来记录。
|
||||
|
||||
如果是二维数组,来记录两个点链接,例如 parent[节点编号A][节点编号B] = 1 ,parent[节点编号B][节点编号A] = 1,来表示 节点A 与 节点B 相连,那就没有上面说的这个注意事项了,当然这么做的话,就是多开辟的内存空间。
|
||||
如果是二维数组,来记录两个点链接,例如 parent[节点编号A][节点编号B] = 1 ,parent[节点编号B][节点编号A] = 1,来表示节点A与节点B相连,那就没有上面说的这个注意事项了,当然这么做的话,就是多开辟的内存空间。
|
||||
|
||||
以下是输出最小生成树边的代码,不算最后输出, 就额外添加了两行代码,我都注释标记了:
|
||||
以下是输出最小生成树边的代码,不算最后输出,就额外添加了两行代码,我都注释标记了:
|
||||
|
||||
```CPP
|
||||
#include<iostream>
|
||||
@@ -460,7 +460,7 @@ int main() {
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
```
|
||||
|
||||
按照本题示例,代码输入如下:
|
||||
|
||||
@@ -476,40 +476,40 @@ int main() {
|
||||
|
||||
注意,这里是无向图,我在输出上添加了箭头仅仅是为了方便大家看出是边的意思。
|
||||
|
||||
大家可以和我们本题最后生成的最小生成树的图 去对比一下 边的链接情况:
|
||||
大家可以和我们本题最后生成的最小生成树的图去对比一下边的链接情况:
|
||||
|
||||
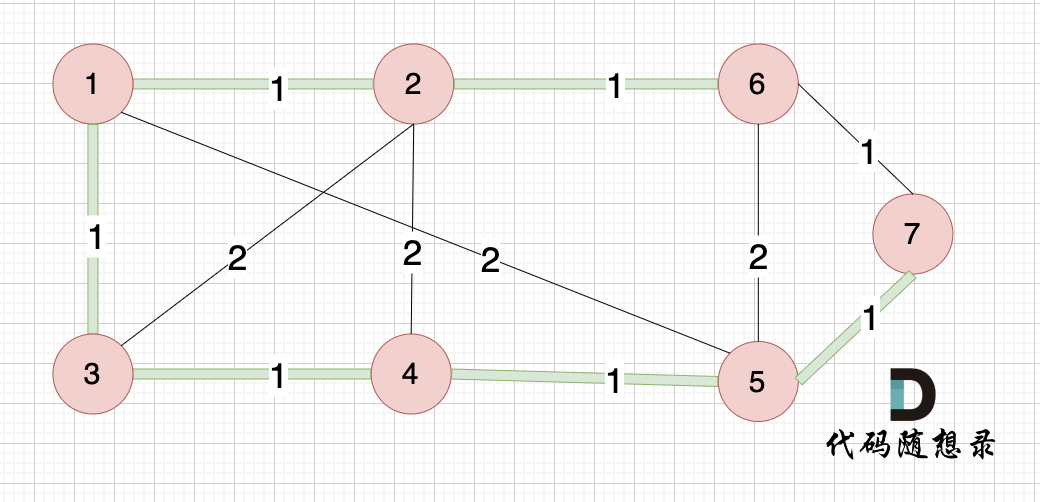
|
||||
|
||||
绿色的边 是最小生成树,和我们的 输出完全一致。
|
||||
绿色的边是最小生成树,和我们的输出完全一致。
|
||||
|
||||
## 总结
|
||||
## 总结
|
||||
|
||||
此时我就把prim算法讲解完毕了,我们再来回顾一下。
|
||||
此时我就把prim算法讲解完毕了,我们再来回顾一下。
|
||||
|
||||
关于 prim算法,我自创了三部曲,来帮助大家理解:
|
||||
关于prim算法,我自创了三部曲,来帮助大家理解:
|
||||
|
||||
1. 第一步,选距离生成树最近节点
|
||||
2. 第二步,最近节点加入生成树
|
||||
2. 第二步,最近节点加入生成树
|
||||
3. 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
|
||||
|
||||
大家只要理解这三部曲, prim算法 至少是可以写出一个框架出来,然后在慢慢补充细节,这样不至于 自己在写prim的时候 两眼一抹黑 完全凭感觉去写。
|
||||
这也为什么很多录友感觉 prim算法比较难,而且每次学会来,隔一段时间 又不会写了,主要是 没有一个纲领。
|
||||
大家只要理解这三部曲,prim算法至少是可以写出一个框架出来,然后在慢慢补充细节,这样不至于自己在写prim的时候两眼一抹黑完全凭感觉去写。
|
||||
这也为什么很多录友感觉prim算法比较难,而且每次学会来,隔一段时间又不会写了,主要是没有一个纲领。
|
||||
|
||||
理解这三部曲之后,更重要的 就是理解 minDist数组。
|
||||
理解这三部曲之后,更重要的就是理解minDist数组。
|
||||
|
||||
**minDist数组 是prim算法的灵魂,它帮助 prim算法完成最重要的一步,就是如何找到 距离最小生成树最近的点**。
|
||||
**minDist数组是prim算法的灵魂,它帮助prim算法完成最重要的一步,就是如何找到距离最小生成树最近的点**。
|
||||
|
||||
再来帮大家回顾 minDist数组 的含义:记录 每一个节点距离最小生成树的最近距离。
|
||||
再来帮大家回顾minDist数组的含义:记录每一个节点距离最小生成树的最近距离。
|
||||
|
||||
理解 minDist数组 ,至少大家看prim算法的代码不会懵。
|
||||
理解minDist数组,至少大家看prim算法的代码不会懵。
|
||||
|
||||
也正是 因为 minDist数组 的作用,我们根据 minDist数组,选取距离 生成树 最近的节点 加入生成树,那么 **minDist数组里记录的其实也是 最小生成树的边的权值**。
|
||||
也正是因为minDist数组的作用,我们根据minDist数组,选取距离生成树最近的节点加入生成树,那么**minDist数组里记录的其实也是最小生成树的边的权值**。
|
||||
|
||||
所以我们求 最小生成树的权值和 就是 计算后的 minDist数组 数值总和。
|
||||
所以我们求最小生成树的权值和就是计算后的minDist数组数值总和。
|
||||
|
||||
最后我们拓展了如何求职 最小生成树 的每一条边,其实 添加的代码很简单,主要是理解 为什么使用 parent数组 来记录边 以及 在哪里 更新parent数组。
|
||||
最后我们拓展了如何获得最小生成树的每一条边,其实添加的代码很简单,主要是理解为什么使用parent数组来记录边以及在哪里更新parent数组。
|
||||
|
||||
同时,因为使用一维数组,数组的下标和数组 如何赋值很重要,不要搞反,导致结果被覆盖。
|
||||
同时,因为使用一维数组,数组的下标和数组如何赋值很重要,不要搞反,导致结果被覆盖。
|
||||
|
||||
好了,以上为总结,录友们学习愉快。
|
||||
|
||||
|
||||
@@ -464,6 +464,60 @@ if __name__ == "__main__":
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
async function main() {
|
||||
// 輸入
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const [n, m] = (await readline()).split(" ").map(Number)
|
||||
const grid = {}
|
||||
for (let i = 0 ; i < m ; i++) {
|
||||
const [src, desc, w] = (await readline()).split(" ").map(Number)
|
||||
if (grid.hasOwnProperty(src)) {
|
||||
grid[src].push([desc, w])
|
||||
} else {
|
||||
grid[src] = [[desc, w]]
|
||||
}
|
||||
}
|
||||
const minDist = Array.from({length: n + 1}, () => Number.MAX_VALUE)
|
||||
|
||||
// 起始點
|
||||
minDist[1] = 0
|
||||
|
||||
const q = [1]
|
||||
const visited = Array.from({length: n + 1}, () => false)
|
||||
|
||||
while (q.length) {
|
||||
const src = q.shift()
|
||||
const neighbors = grid[src]
|
||||
visited[src] = false
|
||||
if (neighbors) {
|
||||
for (const [desc, w] of neighbors) {
|
||||
if (minDist[src] !== Number.MAX_VALUE
|
||||
&& minDist[src] + w < minDist[desc]) {
|
||||
minDist[desc] = minDist[src] + w
|
||||
if (!visited[desc]) {
|
||||
q.push(desc)
|
||||
visited[desc] = true
|
||||
}
|
||||
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 輸出
|
||||
if (minDist[n] === Number.MAX_VALUE) {
|
||||
console.log('unconnected')
|
||||
} else {
|
||||
console.log(minDist[n])
|
||||
}
|
||||
}
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@@ -485,6 +485,45 @@ if __name__ == "__main__":
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
async function main() {
|
||||
// 輸入
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const [n, m] = (await readline()).split(" ").map(Number)
|
||||
const edges = []
|
||||
for (let i = 0 ; i < m ; i++) {
|
||||
edges.push((await readline()).split(" ").map(Number))
|
||||
}
|
||||
const minDist = Array.from({length: n + 1}, () => Number.MAX_VALUE)
|
||||
// 起始點
|
||||
minDist[1] = 0
|
||||
|
||||
for (let i = 1 ; i < n ; i++) {
|
||||
let update = false
|
||||
for (const [src, desc, w] of edges) {
|
||||
if (minDist[src] !== Number.MAX_VALUE && minDist[src] + w < minDist[desc]) {
|
||||
minDist[desc] = minDist[src] + w
|
||||
update = true
|
||||
}
|
||||
}
|
||||
if (!update) {
|
||||
break;
|
||||
}
|
||||
}
|
||||
|
||||
// 輸出
|
||||
if (minDist[n] === Number.MAX_VALUE) {
|
||||
console.log('unconnected')
|
||||
} else {
|
||||
console.log(minDist[n])
|
||||
}
|
||||
}
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
@@ -54,7 +54,7 @@ circle
|
||||
|
||||
## 思路
|
||||
|
||||
本题是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。
|
||||
本题是 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 延伸题目。
|
||||
|
||||
本题是要我们判断 负权回路,也就是图中出现环且环上的边总权值为负数。
|
||||
|
||||
@@ -64,7 +64,7 @@ circle
|
||||
|
||||
接下来我们来看 如何使用 bellman_ford 算法来判断 负权回路。
|
||||
|
||||
在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中 我们讲了 bellman_ford 算法的核心就是一句话:对 所有边 进行 n-1 次松弛。 同时文中的 【拓展】部分, 我们也讲了 松弛n次以上 会怎么样?
|
||||
在 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 中 我们讲了 bellman_ford 算法的核心就是一句话:对 所有边 进行 n-1 次松弛。 同时文中的 【拓展】部分, 我们也讲了 松弛n次以上 会怎么样?
|
||||
|
||||
在没有负权回路的图中,松弛 n 次以上 ,结果不会有变化。
|
||||
|
||||
@@ -72,7 +72,7 @@ circle
|
||||
|
||||
那么每松弛一次,都会更新最短路径,所以结果会一直有变化。
|
||||
|
||||
(如果对于 bellman_ford 不了解的录友,建议详细看这里:[kama94.城市间货物运输I](./kama94.城市间货物运输I.md))
|
||||
(如果对于 bellman_ford 不了解的录友,建议详细看这里:[kama94.城市间货物运输I](./0094.城市间货物运输I.md))
|
||||
|
||||
以上为理论分析,接下来我们再画图举例。
|
||||
|
||||
@@ -94,13 +94,13 @@ circle
|
||||
|
||||
如果在负权回路多绕两圈,三圈,无穷圈,那么我们的总成本就会无限小, 如果要求最小成本的话,你会发现本题就无解了。
|
||||
|
||||
在 bellman_ford 算法中,松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径,松弛 n 次以上,minDist数组(记录起到到其他节点的最短距离)中的结果也不会有改变 (如果对 bellman_ford 算法 不了解,也不知道 minDist 是什么,建议详看上篇讲解[kama94.城市间货物运输I](./kama94.城市间货物运输I.md))
|
||||
在 bellman_ford 算法中,松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径,松弛 n 次以上,minDist数组(记录起到到其他节点的最短距离)中的结果也不会有改变 (如果对 bellman_ford 算法 不了解,也不知道 minDist 是什么,建议详看上篇讲解[kama94.城市间货物运输I](./0094.城市间货物运输I.md))
|
||||
|
||||
而本题有负权回路的情况下,一直都会有更短的最短路,所以 松弛 第n次,minDist数组 也会发生改变。
|
||||
|
||||
那么解决本题的 核心思路,就是在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的基础上,再多松弛一次,看minDist数组 是否发生变化。
|
||||
那么解决本题的 核心思路,就是在 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 的基础上,再多松弛一次,看minDist数组 是否发生变化。
|
||||
|
||||
代码和 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 基本是一样的,如下:(关键地方已注释)
|
||||
代码和 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 基本是一样的,如下:(关键地方已注释)
|
||||
|
||||
```CPP
|
||||
#include <iostream>
|
||||
|
||||
@@ -51,15 +51,15 @@
|
||||
|
||||
## 思路
|
||||
|
||||
本题为单源有限最短路问题,同样是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 延伸题目。
|
||||
本题为单源有限最短路问题,同样是 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 延伸题目。
|
||||
|
||||
注意题目中描述是 **最多经过 k 个城市的条件下,而不是一定经过k个城市,也可以经过的城市数量比k小,但要最短的路径**。
|
||||
|
||||
在 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 中我们讲了:**对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。
|
||||
在 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 中我们讲了:**对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离**。
|
||||
|
||||
节点数量为n,起点到终点,最多是 n-1 条边相连。 那么对所有边松弛 n-1 次 就一定能得到 起点到达 终点的最短距离。
|
||||
|
||||
(如果对以上讲解看不懂,建议详看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) )
|
||||
(如果对以上讲解看不懂,建议详看 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) )
|
||||
|
||||
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图:
|
||||
|
||||
@@ -71,7 +71,7 @@
|
||||
|
||||
对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离,那么对所有边松弛 k + 1次,就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。
|
||||
|
||||
**注意**: 本题是 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 的拓展题,如果对 bellman_ford 没有深入了解,强烈建议先看 [kama94.城市间货物运输I](./kama94.城市间货物运输I.md) 再做本题。
|
||||
**注意**: 本题是 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 的拓展题,如果对 bellman_ford 没有深入了解,强烈建议先看 [kama94.城市间货物运输I](./0094.城市间货物运输I.md) 再做本题。
|
||||
|
||||
理解以上内容,其实本题代码就很容易了,bellman_ford 标准写法是松弛 n-1 次,本题就松弛 k + 1次就好。
|
||||
|
||||
@@ -366,19 +366,19 @@ int main() {
|
||||
|
||||
## 拓展二(本题本质)
|
||||
|
||||
那么前面讲解过的 [94.城市间货物运输I](./kama94.城市间货物运输I.md) 和 [95.城市间货物运输II](./kama95.城市间货物运输II.md) 也是bellman_ford经典算法,也没使用 minDist_copy,怎么就没问题呢?
|
||||
那么前面讲解过的 [94.城市间货物运输I](./0094.城市间货物运输I.md) 和 [95.城市间货物运输II](./0095.城市间货物运输II.md) 也是bellman_ford经典算法,也没使用 minDist_copy,怎么就没问题呢?
|
||||
|
||||
> 如果没看过我上面这两篇讲解的话,建议详细学习上面两篇,再看我下面讲的区别,否则容易看不懂。
|
||||
|
||||
[94.城市间货物运输I](./kama94.城市间货物运输I.md), 是没有 负权回路的,那么 多松弛多少次,对结果都没有影响。
|
||||
[94.城市间货物运输I](./0094.城市间货物运输I.md), 是没有 负权回路的,那么 多松弛多少次,对结果都没有影响。
|
||||
|
||||
求 节点1 到 节点n 的最短路径,松弛n-1 次就够了,松弛 大于 n-1次,结果也不会变。
|
||||
|
||||
那么在对所有边进行第一次松弛的时候,如果基于 本次计算的 minDist 来计算 minDist (相当于多做松弛了),也是对最终结果没影响。
|
||||
|
||||
[95.城市间货物运输II](./kama95.城市间货物运输II.md) 是判断是否有 负权回路,一旦有负权回路, 对所有边松弛 n-1 次以后,在做松弛 minDist 数值一定会变,根据这一点来判断是否有负权回路。
|
||||
[95.城市间货物运输II](./0095.城市间货物运输II.md) 是判断是否有 负权回路,一旦有负权回路, 对所有边松弛 n-1 次以后,在做松弛 minDist 数值一定会变,根据这一点来判断是否有负权回路。
|
||||
|
||||
所以,[95.城市间货物运输II](./kama95.城市间货物运输II.md) 只需要判断minDist数值变化了就行,而 minDist 的数值对不对,并不是我们关心的。
|
||||
所以,[95.城市间货物运输II](./0095.城市间货物运输II.md) 只需要判断minDist数值变化了就行,而 minDist 的数值对不对,并不是我们关心的。
|
||||
|
||||
那么本题 为什么计算minDist 一定要基于上次 的 minDist 数值。
|
||||
|
||||
@@ -703,6 +703,42 @@ public class Main {
|
||||
```
|
||||
|
||||
### Python
|
||||
```python
|
||||
def main():
|
||||
# 輸入
|
||||
n, m = map(int, input().split())
|
||||
edges = list()
|
||||
for _ in range(m):
|
||||
edges.append(list(map(int, input().split() )))
|
||||
|
||||
start, end, k = map(int, input().split())
|
||||
min_dist = [float('inf') for _ in range(n + 1)]
|
||||
min_dist[start] = 0
|
||||
|
||||
# 只能經過k個城市,所以從起始點到中間有(k + 1)個邊連接
|
||||
# 需要鬆弛(k + 1)次
|
||||
|
||||
for _ in range(k + 1):
|
||||
update = False
|
||||
min_dist_copy = min_dist.copy()
|
||||
for src, desc, w in edges:
|
||||
if (min_dist_copy[src] != float('inf') and
|
||||
min_dist_copy[src] + w < min_dist[desc]):
|
||||
min_dist[desc] = min_dist_copy[src] + w
|
||||
update = True
|
||||
if not update:
|
||||
break
|
||||
# 輸出
|
||||
if min_dist[end] == float('inf'):
|
||||
print('unreachable')
|
||||
else:
|
||||
print(min_dist[end])
|
||||
|
||||
|
||||
|
||||
if __name__ == "__main__":
|
||||
main()
|
||||
```
|
||||
|
||||
### Go
|
||||
|
||||
|
||||
@@ -277,7 +277,7 @@ ACM格式大家在输出结果的时候,要关注看看格式问题,特别
|
||||
|
||||
有录友可能会想,ACM格式就是麻烦,有空格没有空格有什么影响,结果对了不就行了?
|
||||
|
||||
ACM模式相对于核心代码模式(力扣) 更考验大家对代码的掌控能力。 例如工程代码里,输出输出都是要自己控制的。这也是为什么大公司笔试,都是ACM模式。
|
||||
ACM模式相对于核心代码模式(力扣) 更考验大家对代码的掌控能力。 例如工程代码里,输入输出都是要自己控制的。这也是为什么大公司笔试,都是ACM模式。
|
||||
|
||||
以上代码中,结果都存在了 result数组里(二维数组,每一行是一个结果),最后将其打印出来。(重点看注释)
|
||||
|
||||
|
||||
@@ -499,6 +499,55 @@ main();
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
```scala
|
||||
import scala.collection.mutable.Queue
|
||||
import util.control.Breaks._
|
||||
|
||||
// Dev on LeetCode: https://leetcode.cn/problems/number-of-islands/description/
|
||||
object Solution {
|
||||
def numIslands(grid: Array[Array[Char]]): Int = {
|
||||
val row = grid.length
|
||||
val col = grid(0).length
|
||||
val dir = List((-1,0), (0,-1), (1,0), (0,1)) // 四个方向
|
||||
var visited = Array.fill(row)(Array.fill(col)(false))
|
||||
var counter = 0
|
||||
var que = Queue.empty[Tuple2[Int, Int]]
|
||||
|
||||
(0 until row).map{ r =>
|
||||
(0 until col).map{ c =>
|
||||
breakable {
|
||||
if (!visited(r)(c) && grid(r)(c) == '1') {
|
||||
que.enqueue((r, c))
|
||||
visited(r)(c) // 只要加入队列,立刻标记
|
||||
} else break // 不是岛屿不进入queue,也不记录
|
||||
|
||||
while (!que.isEmpty) {
|
||||
val cur = que.head
|
||||
que.dequeue()
|
||||
val x = cur(0)
|
||||
val y = cur(1)
|
||||
dir.map{ d =>
|
||||
val nextX = x + d(0)
|
||||
val nextY = y + d(1)
|
||||
breakable {
|
||||
// 越界就跳过
|
||||
if (nextX < 0 || nextX >= row || nextY < 0 || nextY >= col) break
|
||||
if (!visited(nextX)(nextY) && grid(nextX)(nextY) == '1') {
|
||||
visited(nextX)(nextY) = true // 只要加入队列,立刻标记
|
||||
que.enqueue((nextX, nextY))
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
counter = counter + 1 // 找完一个岛屿后记录一下
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
counter
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### C#
|
||||
|
||||
|
||||
@@ -412,6 +412,46 @@ const dfs = (graph, visited, x, y) => {
|
||||
### Swift
|
||||
|
||||
### Scala
|
||||
```scala
|
||||
import util.control.Breaks._
|
||||
|
||||
object Solution {
|
||||
val dir = List((-1,0), (0,-1), (1,0), (0,1)) // 四个方向
|
||||
|
||||
def dfs(grid: Array[Array[Char]], visited: Array[Array[Boolean]], row: Int, col: Int): Unit = {
|
||||
(0 until 4).map { x =>
|
||||
val nextR = row + dir(x)(0)
|
||||
val nextC = col + dir(x)(1)
|
||||
breakable {
|
||||
if(nextR < 0 || nextR >= grid.length || nextC < 0 || nextC >= grid(0).length) break
|
||||
if (!visited(nextR)(nextC) && grid(nextR)(nextC) == '1') {
|
||||
visited(nextR)(nextC) = true // 经过就记录
|
||||
dfs(grid, visited, nextR, nextC)
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
def numIslands(grid: Array[Array[Char]]): Int = {
|
||||
val row = grid.length
|
||||
val col = grid(0).length
|
||||
var visited = Array.fill(row)(Array.fill(col)(false))
|
||||
var counter = 0
|
||||
|
||||
(0 until row).map{ r =>
|
||||
(0 until col).map{ c =>
|
||||
if (!visited(r)(c) && grid(r)(c) == '1') {
|
||||
visited(r)(c) = true // 经过就记录
|
||||
dfs(grid, visited, r, c)
|
||||
counter += 1
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
counter
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
### C#
|
||||
|
||||
|
||||
@@ -222,8 +222,128 @@ public:
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
### Java
|
||||
|
||||
```java
|
||||
import java.util.*;
|
||||
import java.math.*;
|
||||
|
||||
/**
|
||||
* DFS版
|
||||
*/
|
||||
public class Main{
|
||||
|
||||
static final int[][] dir={{0,1},{1,0},{0,-1},{-1,0}};
|
||||
static int result=0;
|
||||
static int count=0;
|
||||
|
||||
public static void main(String[] args){
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
int[][] map = new int[n][m];
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
map[i][j]=scanner.nextInt();
|
||||
}
|
||||
}
|
||||
boolean[][] visited = new boolean[n][m];
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if(!visited[i][j]&&map[i][j]==1){
|
||||
count=0;
|
||||
dfs(map,visited,i,j);
|
||||
result= Math.max(count, result);
|
||||
}
|
||||
}
|
||||
}
|
||||
System.out.println(result);
|
||||
}
|
||||
|
||||
static void dfs(int[][] map,boolean[][] visited,int x,int y){
|
||||
count++;
|
||||
visited[x][y]=true;
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextX=x+dir[i][0];
|
||||
int nextY=y+dir[i][1];
|
||||
//水或者已经访问过的跳过
|
||||
if(nextX<0||nextY<0
|
||||
||nextX>=map.length||nextY>=map[0].length
|
||||
||visited[nextX][nextY]||map[nextX][nextY]==0)continue;
|
||||
|
||||
dfs(map,visited,nextX,nextY);
|
||||
}
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
```java
|
||||
import java.util.*;
|
||||
import java.math.*;
|
||||
|
||||
/**
|
||||
* BFS版
|
||||
*/
|
||||
public class Main {
|
||||
static class Node {
|
||||
int x;
|
||||
int y;
|
||||
|
||||
public Node(int x, int y) {
|
||||
this.x = x;
|
||||
this.y = y;
|
||||
}
|
||||
}
|
||||
|
||||
static final int[][] dir = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
|
||||
static int result = 0;
|
||||
static int count = 0;
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
int m = scanner.nextInt();
|
||||
int[][] map = new int[n][m];
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
map[i][j] = scanner.nextInt();
|
||||
}
|
||||
}
|
||||
boolean[][] visited = new boolean[n][m];
|
||||
for (int i = 0; i < n; i++) {
|
||||
for (int j = 0; j < m; j++) {
|
||||
if (!visited[i][j] && map[i][j] == 1) {
|
||||
count = 0;
|
||||
bfs(map, visited, i, j);
|
||||
result = Math.max(count, result);
|
||||
|
||||
}
|
||||
}
|
||||
}
|
||||
System.out.println(result);
|
||||
}
|
||||
|
||||
static void bfs(int[][] map, boolean[][] visited, int x, int y) {
|
||||
Queue<Node> q = new LinkedList<>();
|
||||
q.add(new Node(x, y));
|
||||
visited[x][y] = true;
|
||||
count++;
|
||||
while (!q.isEmpty()) {
|
||||
Node node = q.remove();
|
||||
for (int i = 0; i < 4; i++) {
|
||||
int nextX = node.x + dir[i][0];
|
||||
int nextY = node.y + dir[i][1];
|
||||
if (nextX < 0 || nextY < 0 || nextX >= map.length || nextY >= map[0].length || visited[nextX][nextY] || map[nextX][nextY] == 0)
|
||||
continue;
|
||||
q.add(new Node(nextX, nextY));
|
||||
visited[nextX][nextY] = true;
|
||||
count++;
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
### Python
|
||||
|
||||
DFS
|
||||
@@ -389,6 +509,144 @@ func main() {
|
||||
|
||||
|
||||
### Rust
|
||||
DFS
|
||||
|
||||
``` rust
|
||||
use std::io;
|
||||
use std::cmp;
|
||||
|
||||
// 定义四个方向
|
||||
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
|
||||
|
||||
fn dfs(grid: &Vec<Vec<i32>>, visited: &mut Vec<Vec<bool>>, x: usize, y: usize, count: &mut i32) {
|
||||
if visited[x][y] || grid[x][y] == 0 {
|
||||
return; // 终止条件:已访问或者遇到海水
|
||||
}
|
||||
visited[x][y] = true; // 标记已访问
|
||||
*count += 1;
|
||||
|
||||
for &(dx, dy) in DIRECTIONS.iter() {
|
||||
let new_x = x as i32 + dx;
|
||||
let new_y = y as i32 + dy;
|
||||
|
||||
// 检查边界条件
|
||||
if new_x >= 0 && new_x < grid.len() as i32 && new_y >= 0 && new_y < grid[0].len() as i32 {
|
||||
dfs(grid, visited, new_x as usize, new_y as usize, count);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
fn main() {
|
||||
let mut input = String::new();
|
||||
|
||||
// 读取 n 和 m
|
||||
io::stdin().read_line(&mut input);
|
||||
let dims: Vec<usize> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
|
||||
let (n, m) = (dims[0], dims[1]);
|
||||
|
||||
// 读取 grid
|
||||
let mut grid = vec![];
|
||||
for _ in 0..n {
|
||||
input.clear();
|
||||
io::stdin().read_line(&mut input);
|
||||
let row: Vec<i32> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
|
||||
grid.push(row);
|
||||
}
|
||||
|
||||
// 初始化访问记录
|
||||
let mut visited = vec![vec![false; m]; n];
|
||||
let mut result = 0;
|
||||
|
||||
// 遍历所有格子
|
||||
for i in 0..n {
|
||||
for j in 0..m {
|
||||
if !visited[i][j] && grid[i][j] == 1 {
|
||||
let mut count = 0;
|
||||
dfs(&grid, &mut visited, i, j, &mut count);
|
||||
result = cmp::max(result, count);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 输出结果
|
||||
println!("{}", result);
|
||||
}
|
||||
|
||||
```
|
||||
BFS
|
||||
```rust
|
||||
use std::io;
|
||||
use std::collections::VecDeque;
|
||||
|
||||
// 定义四个方向
|
||||
const DIRECTIONS: [(i32, i32); 4] = [(0, 1), (1, 0), (-1, 0), (0, -1)];
|
||||
|
||||
fn bfs(grid: &Vec<Vec<i32>>, visited: &mut Vec<Vec<bool>>, x: usize, y: usize) -> i32 {
|
||||
let mut count = 0;
|
||||
let mut queue = VecDeque::new();
|
||||
queue.push_back((x, y));
|
||||
visited[x][y] = true; // 标记已访问
|
||||
|
||||
while let Some((cur_x, cur_y)) = queue.pop_front() {
|
||||
count += 1; // 增加计数
|
||||
|
||||
for &(dx, dy) in DIRECTIONS.iter() {
|
||||
let new_x = cur_x as i32 + dx;
|
||||
let new_y = cur_y as i32 + dy;
|
||||
|
||||
// 检查边界条件
|
||||
if new_x >= 0 && new_x < grid.len() as i32 && new_y >= 0 && new_y < grid[0].len() as i32 {
|
||||
let new_x_usize = new_x as usize;
|
||||
let new_y_usize = new_y as usize;
|
||||
|
||||
// 如果未访问且是陆地,加入队列
|
||||
if !visited[new_x_usize][new_y_usize] && grid[new_x_usize][new_y_usize] == 1 {
|
||||
visited[new_x_usize][new_y_usize] = true; // 标记已访问
|
||||
queue.push_back((new_x_usize, new_y_usize));
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
count
|
||||
}
|
||||
|
||||
fn main() {
|
||||
let mut input = String::new();
|
||||
|
||||
// 读取 n 和 m
|
||||
io::stdin().read_line(&mut input).expect("Failed to read line");
|
||||
let dims: Vec<usize> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
|
||||
let (n, m) = (dims[0], dims[1]);
|
||||
|
||||
// 读取 grid
|
||||
let mut grid = vec![];
|
||||
for _ in 0..n {
|
||||
input.clear();
|
||||
io::stdin().read_line(&mut input).expect("Failed to read line");
|
||||
let row: Vec<i32> = input.trim().split_whitespace().map(|s| s.parse().unwrap()).collect();
|
||||
grid.push(row);
|
||||
}
|
||||
|
||||
// 初始化访问记录
|
||||
let mut visited = vec![vec![false; m]; n];
|
||||
let mut result = 0;
|
||||
|
||||
// 遍历所有格子
|
||||
for i in 0..n {
|
||||
for j in 0..m {
|
||||
if !visited[i][j] && grid[i][j] == 1 {
|
||||
let count = bfs(&grid, &mut visited, i, j);
|
||||
result = result.max(count);
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
// 输出结果
|
||||
println!("{}", result);
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### Javascript
|
||||
|
||||
|
||||
@@ -250,105 +250,131 @@ int main() {
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
|
||||
```java
|
||||
import java.util.ArrayList;
|
||||
import java.util.List;
|
||||
import java.util.Scanner;
|
||||
import java.util.*;
|
||||
|
||||
/*
|
||||
* 冗余连接II。主要问题是存在入度为2或者成环,也可能两个问题同时存在。
|
||||
* 1.判断入度为2的边
|
||||
* 2.判断是否成环(并查集)
|
||||
*/
|
||||
|
||||
public class Main {
|
||||
static int n;
|
||||
static int[] father = new int[1001]; // 并查集数组
|
||||
/**
|
||||
* 并查集模板
|
||||
*/
|
||||
static class Disjoint {
|
||||
|
||||
// 并查集初始化
|
||||
public static void init() {
|
||||
for (int i = 1; i <= n; ++i) {
|
||||
father[i] = i;
|
||||
}
|
||||
}
|
||||
private final int[] father;
|
||||
|
||||
// 并查集里寻根的过程
|
||||
public static int find(int u) {
|
||||
if (u == father[u]) return u;
|
||||
return father[u] = find(father[u]); // 路径压缩
|
||||
}
|
||||
|
||||
// 将 v->u 这条边加入并查集
|
||||
public static void join(int u, int v) {
|
||||
u = find(u);
|
||||
v = find(v);
|
||||
if (u != v) {
|
||||
father[v] = u; // 合并两棵树
|
||||
}
|
||||
}
|
||||
|
||||
// 判断 u 和 v 是否有同一个根
|
||||
public static boolean same(int u, int v) {
|
||||
return find(u) == find(v);
|
||||
}
|
||||
|
||||
// 在有向图里找到删除的那条边,使其变成树
|
||||
public static void getRemoveEdge(List<int[]> edges) {
|
||||
init(); // 初始化并查集
|
||||
for (int i = 0; i < n; i++) { // 遍历所有的边
|
||||
if (same(edges.get(i)[0], edges.get(i)[1])) { // 如果构成有向环了,就是要删除的边
|
||||
System.out.println(edges.get(i)[0] + " " + edges.get(i)[1]);
|
||||
return;
|
||||
} else {
|
||||
join(edges.get(i)[0], edges.get(i)[1]);
|
||||
public Disjoint(int n) {
|
||||
father = new int[n];
|
||||
for (int i = 0; i < n; i++) {
|
||||
father[i] = i;
|
||||
}
|
||||
}
|
||||
|
||||
public void join(int n, int m) {
|
||||
n = find(n);
|
||||
m = find(m);
|
||||
if (n == m) return;
|
||||
father[n] = m;
|
||||
}
|
||||
|
||||
public int find(int n) {
|
||||
return father[n] == n ? n : (father[n] = find(father[n]));
|
||||
}
|
||||
|
||||
public boolean isSame(int n, int m) {
|
||||
return find(n) == find(m);
|
||||
}
|
||||
}
|
||||
|
||||
// 删一条边之后判断是不是树
|
||||
public static boolean isTreeAfterRemoveEdge(List<int[]> edges, int deleteEdge) {
|
||||
init(); // 初始化并查集
|
||||
static class Edge {
|
||||
int s;
|
||||
int t;
|
||||
|
||||
public Edge(int s, int t) {
|
||||
this.s = s;
|
||||
this.t = t;
|
||||
}
|
||||
}
|
||||
|
||||
static class Node {
|
||||
int id;
|
||||
int in;
|
||||
int out;
|
||||
}
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
List<Edge> edges = new ArrayList<>();
|
||||
Node[] nodeMap = new Node[n + 1];
|
||||
for (int i = 1; i <= n; i++) {
|
||||
nodeMap[i] = new Node();
|
||||
}
|
||||
Integer doubleIn = null;
|
||||
for (int i = 0; i < n; i++) {
|
||||
if (i == deleteEdge) continue;
|
||||
if (same(edges.get(i)[0], edges.get(i)[1])) { // 如果构成有向环了,一定不是树
|
||||
int s = scanner.nextInt();
|
||||
int t = scanner.nextInt();
|
||||
//记录入度
|
||||
nodeMap[t].in++;
|
||||
if (!(nodeMap[t].in < 2)) doubleIn = t;
|
||||
Edge edge = new Edge(s, t);
|
||||
edges.add(edge);
|
||||
}
|
||||
Edge result = null;
|
||||
//存在入度为2的节点,既要消除入度为2的问题同时解除可能存在的环
|
||||
if (doubleIn != null) {
|
||||
List<Edge> doubleInEdges = new ArrayList<>();
|
||||
for (Edge edge : edges) {
|
||||
if (edge.t == doubleIn) doubleInEdges.add(edge);
|
||||
if (doubleInEdges.size() == 2) break;
|
||||
}
|
||||
Edge edge = doubleInEdges.get(1);
|
||||
if (isTreeWithExclude(edges, edge, nodeMap)) {
|
||||
result = edge;
|
||||
} else {
|
||||
result = doubleInEdges.get(0);
|
||||
}
|
||||
} else {
|
||||
//不存在入度为2的节点,则只需要解除环即可
|
||||
result = getRemoveEdge(edges, nodeMap);
|
||||
}
|
||||
|
||||
System.out.println(result.s + " " + result.t);
|
||||
}
|
||||
|
||||
public static boolean isTreeWithExclude(List<Edge> edges, Edge exculdEdge, Node[] nodeMap) {
|
||||
Disjoint disjoint = new Disjoint(nodeMap.length + 1);
|
||||
for (Edge edge : edges) {
|
||||
if (edge == exculdEdge) continue;
|
||||
//成环则不是树
|
||||
if (disjoint.isSame(edge.s, edge.t)) {
|
||||
return false;
|
||||
}
|
||||
join(edges.get(i)[0], edges.get(i)[1]);
|
||||
disjoint.join(edge.s, edge.t);
|
||||
}
|
||||
return true;
|
||||
}
|
||||
|
||||
public static void main(String[] args) {
|
||||
Scanner sc = new Scanner(System.in);
|
||||
List<int[]> edges = new ArrayList<>(); // 存储所有的边
|
||||
public static Edge getRemoveEdge(List<Edge> edges, Node[] nodeMap) {
|
||||
int length = nodeMap.length;
|
||||
Disjoint disjoint = new Disjoint(length);
|
||||
|
||||
n = sc.nextInt(); // 顶点数
|
||||
int[] inDegree = new int[n + 1]; // 记录每个节点的入度
|
||||
for (int i = 0; i < n; i++) {
|
||||
int s = sc.nextInt(); // 边的起点
|
||||
int t = sc.nextInt(); // 边的终点
|
||||
inDegree[t]++;
|
||||
edges.add(new int[]{s, t}); // 将边加入列表
|
||||
for (Edge edge : edges) {
|
||||
if (disjoint.isSame(edge.s, edge.t)) return edge;
|
||||
disjoint.join(edge.s, edge.t);
|
||||
}
|
||||
|
||||
List<Integer> vec = new ArrayList<>(); // 记录入度为2的边(如果有的话就两条边)
|
||||
// 找入度为2的节点所对应的边,注意要倒序,因为优先删除最后出现的一条边
|
||||
for (int i = n - 1; i >= 0; i--) {
|
||||
if (inDegree[edges.get(i)[1]] == 2) {
|
||||
vec.add(i);
|
||||
}
|
||||
}
|
||||
|
||||
// 情况一、情况二
|
||||
if (vec.size() > 0) {
|
||||
// vec里的边已经按照倒叙放的,所以优先删 vec.get(0) 这条边
|
||||
if (isTreeAfterRemoveEdge(edges, vec.get(0))) {
|
||||
System.out.println(edges.get(vec.get(0))[0] + " " + edges.get(vec.get(0))[1]);
|
||||
} else {
|
||||
System.out.println(edges.get(vec.get(1))[0] + " " + edges.get(vec.get(1))[1]);
|
||||
}
|
||||
return;
|
||||
}
|
||||
|
||||
// 处理情况三:明确没有入度为2的情况,一定有有向环,找到构成环的边返回即可
|
||||
getRemoveEdge(edges);
|
||||
return null;
|
||||
}
|
||||
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
### Python
|
||||
|
||||
```python
|
||||
|
||||
@@ -152,66 +152,70 @@ int main() {
|
||||
|
||||
## 其他语言版本
|
||||
|
||||
### Java
|
||||
### Java
|
||||
|
||||
```Java
|
||||
import java.util.*;
|
||||
|
||||
public class Main {
|
||||
// BFS方法
|
||||
public static int ladderLength(String beginWord, String endWord, List<String> wordList) {
|
||||
// 使用set作为查询容器,效率更高
|
||||
HashSet<String> set = new HashSet<>(wordList);
|
||||
|
||||
// 声明一个queue存储每次变更一个字符得到的且存在于容器中的新字符串
|
||||
Queue<String> queue = new LinkedList<>();
|
||||
|
||||
// 声明一个hashMap存储遍历到的字符串以及所走过的路径path
|
||||
HashMap<String, Integer> visitMap = new HashMap<>();
|
||||
queue.offer(beginWord);
|
||||
visitMap.put(beginWord, 1);
|
||||
|
||||
while (!queue.isEmpty()) {
|
||||
String curWord = queue.poll();
|
||||
int path = visitMap.get(curWord);
|
||||
public static void main(String[] args) {
|
||||
Scanner scanner = new Scanner(System.in);
|
||||
int n = scanner.nextInt();
|
||||
scanner.nextLine();
|
||||
String beginStr = scanner.next();
|
||||
String endStr = scanner.next();
|
||||
scanner.nextLine();
|
||||
List<String> wordList = new ArrayList<>();
|
||||
wordList.add(beginStr);
|
||||
wordList.add(endStr);
|
||||
for (int i = 0; i < n; i++) {
|
||||
wordList.add(scanner.nextLine());
|
||||
}
|
||||
int count = bfs(beginStr, endStr, wordList);
|
||||
System.out.println(count);
|
||||
}
|
||||
|
||||
for (int i = 0; i < curWord.length(); i++) {
|
||||
char[] ch = curWord.toCharArray();
|
||||
// 每个位置尝试26个字母
|
||||
for (char k = 'a'; k <= 'z'; k++) {
|
||||
ch[i] = k;
|
||||
|
||||
String newWord = new String(ch);
|
||||
if (newWord.equals(endWord)) return path + 1;
|
||||
|
||||
// 如果这个新字符串存在于容器且之前未被访问到
|
||||
if (set.contains(newWord) && !visitMap.containsKey(newWord)) {
|
||||
visitMap.put(newWord, path + 1);
|
||||
queue.offer(newWord);
|
||||
/**
|
||||
* 广度优先搜索-寻找最短路径
|
||||
*/
|
||||
public static int bfs(String beginStr, String endStr, List<String> wordList) {
|
||||
int len = 1;
|
||||
Set<String> set = new HashSet<>(wordList);
|
||||
Set<String> visited = new HashSet<>();
|
||||
Queue<String> q = new LinkedList<>();
|
||||
visited.add(beginStr);
|
||||
q.add(beginStr);
|
||||
q.add(null);
|
||||
while (!q.isEmpty()) {
|
||||
String node = q.remove();
|
||||
//上一层结束,若下一层还有节点进入下一层
|
||||
if (node == null) {
|
||||
if (!q.isEmpty()) {
|
||||
len++;
|
||||
q.add(null);
|
||||
}
|
||||
continue;
|
||||
}
|
||||
char[] charArray = node.toCharArray();
|
||||
//寻找邻接节点
|
||||
for (int i = 0; i < charArray.length; i++) {
|
||||
//记录旧值,用于回滚修改
|
||||
char old = charArray[i];
|
||||
for (char j = 'a'; j <= 'z'; j++) {
|
||||
charArray[i] = j;
|
||||
String newWord = new String(charArray);
|
||||
if (set.contains(newWord) && !visited.contains(newWord)) {
|
||||
q.add(newWord);
|
||||
visited.add(newWord);
|
||||
//找到结尾
|
||||
if (newWord.equals(endStr)) return len + 1;
|
||||
}
|
||||
}
|
||||
charArray[i] = old;
|
||||
}
|
||||
}
|
||||
|
||||
return 0;
|
||||
}
|
||||
|
||||
public static void main (String[] args) {
|
||||
/* code */
|
||||
// 接收输入
|
||||
Scanner sc = new Scanner(System.in);
|
||||
int N = sc.nextInt();
|
||||
sc.nextLine();
|
||||
String[] strs = sc.nextLine().split(" ");
|
||||
|
||||
List<String> wordList = new ArrayList<>();
|
||||
for (int i = 0; i < N; i++) {
|
||||
wordList.add(sc.nextLine());
|
||||
}
|
||||
|
||||
// wordList.add(strs[1]);
|
||||
|
||||
// 打印结果
|
||||
int result = ladderLength(strs[0], strs[1], wordList);
|
||||
System.out.println(result);
|
||||
}
|
||||
}
|
||||
|
||||
```
|
||||
|
||||
@@ -375,6 +375,131 @@ for _ in range(n):
|
||||
|
||||
### Javascript
|
||||
|
||||
```js
|
||||
class MinHeap {
|
||||
constructor() {
|
||||
this.val = []
|
||||
}
|
||||
push(val) {
|
||||
this.val.push(val)
|
||||
if (this.val.length > 1) {
|
||||
this.bubbleUp()
|
||||
}
|
||||
}
|
||||
bubbleUp() {
|
||||
let pi = this.val.length - 1
|
||||
let pp = Math.floor((pi - 1) / 2)
|
||||
while (pi > 0 && this.val[pp][0] > this.val[pi][0]) {
|
||||
;[this.val[pi], this.val[pp]] = [this.val[pp], this.val[pi]]
|
||||
pi = pp
|
||||
pp = Math.floor((pi - 1) / 2)
|
||||
}
|
||||
}
|
||||
pop() {
|
||||
if (this.val.length > 1) {
|
||||
let pp = 0
|
||||
let pi = this.val.length - 1
|
||||
;[this.val[pi], this.val[pp]] = [this.val[pp], this.val[pi]]
|
||||
const min = this.val.pop()
|
||||
if (this.val.length > 1) {
|
||||
this.sinkDown(0)
|
||||
}
|
||||
return min
|
||||
} else if (this.val.length == 1) {
|
||||
return this.val.pop()
|
||||
}
|
||||
|
||||
}
|
||||
sinkDown(parentIdx) {
|
||||
let pp = parentIdx
|
||||
let plc = pp * 2 + 1
|
||||
let prc = pp * 2 + 2
|
||||
let pt = pp // temp pointer
|
||||
if (plc < this.val.length && this.val[pp][0] > this.val[plc][0]) {
|
||||
pt = plc
|
||||
}
|
||||
if (prc < this.val.length && this.val[pt][0] > this.val[prc][0]) {
|
||||
pt = prc
|
||||
}
|
||||
if (pt != pp) {
|
||||
;[this.val[pp], this.val[pt]] = [this.val[pt], this.val[pp]]
|
||||
this.sinkDown(pt)
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
const moves = [
|
||||
[1, 2],
|
||||
[2, 1],
|
||||
[-1, -2],
|
||||
[-2, -1],
|
||||
[-1, 2],
|
||||
[-2, 1],
|
||||
[1, -2],
|
||||
[2, -1]
|
||||
]
|
||||
|
||||
function dist(a, b) {
|
||||
return ((a[0] - b[0])**2 + (a[1] - b[1])**2)**0.5
|
||||
}
|
||||
|
||||
function isValid(x, y) {
|
||||
return x >= 1 && y >= 1 && x < 1001 && y < 1001
|
||||
}
|
||||
|
||||
function bfs(start, end) {
|
||||
const step = new Map()
|
||||
step.set(start.join(" "), 0)
|
||||
const q = new MinHeap()
|
||||
q.push([dist(start, end), start[0], start[1]])
|
||||
|
||||
while(q.val.length) {
|
||||
const [d, x, y] = q.pop()
|
||||
// if x and y correspond to end position output result
|
||||
if (x == end[0] && y == end[1]) {
|
||||
console.log(step.get(end.join(" ")))
|
||||
break;
|
||||
}
|
||||
for (const [dx, dy] of moves) {
|
||||
const nx = dx + x
|
||||
const ny = dy + y
|
||||
if (isValid(nx, ny)) {
|
||||
const newStep = step.get([x, y].join(" ")) + 1
|
||||
const newDist = dist([nx, ny], [...end])
|
||||
const s = step.get([nx, ny].join(" ")) ?
|
||||
step.get([nx, ny]) :
|
||||
Number.MAX_VALUE
|
||||
if (newStep < s) {
|
||||
q.push(
|
||||
[
|
||||
newStep + newDist,
|
||||
nx,
|
||||
ny
|
||||
]
|
||||
)
|
||||
step.set([nx, ny].join(" "), newStep)
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
}
|
||||
|
||||
async function main() {
|
||||
const rl = require('readline').createInterface({ input: process.stdin })
|
||||
const iter = rl[Symbol.asyncIterator]()
|
||||
const readline = async () => (await iter.next()).value
|
||||
const n = Number((await readline()))
|
||||
|
||||
// find min step
|
||||
for (let i = 0 ; i < n ; i++) {
|
||||
const [s1, s2, t1, t2] = (await readline()).split(" ").map(Number)
|
||||
bfs([s1, s2], [t1, t2])
|
||||
}
|
||||
}
|
||||
|
||||
main()
|
||||
```
|
||||
|
||||
### TypeScript
|
||||
|
||||
### PhP
|
||||
|
||||
Reference in New Issue
Block a user