* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
> 要用啥数据结构呢?
# 239. 滑动窗口最大值
[力扣题目链接](https://leetcode.cn/problems/sliding-window-maximum/)
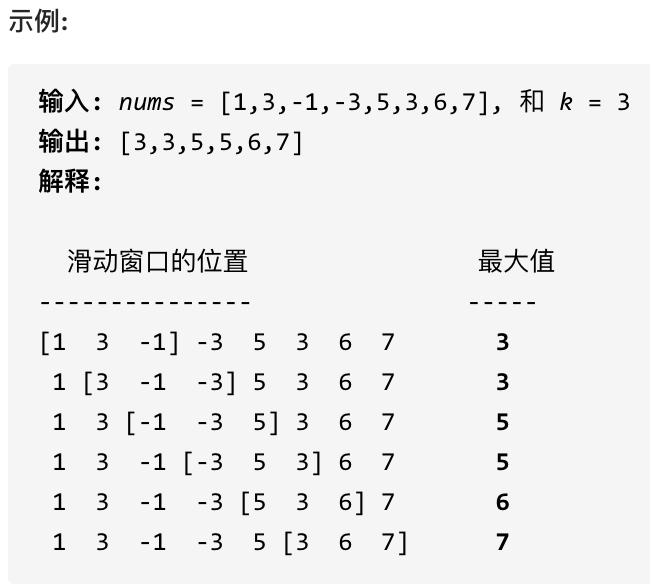
给定一个数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
进阶:
你能在线性时间复杂度内解决此题吗?
 提示:
* 1 <= nums.length <= 10^5
* -10^4 <= nums[i] <= 10^4
* 1 <= k <= nums.length
## 算法公开课
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[单调队列正式登场!| LeetCode:239. 滑动窗口最大值](https://www.bilibili.com/video/BV1XS4y1p7qj),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
这是使用单调队列的经典题目。
难点是如何求一个区间里的最大值呢? (这好像是废话),暴力一下不就得了。
暴力方法,遍历一遍的过程中每次从窗口中再找到最大的数值,这样很明显是O(n × k)的算法。
有的同学可能会想用一个大顶堆(优先级队列)来存放这个窗口里的k个数字,这样就可以知道最大的最大值是多少了, **但是问题是这个窗口是移动的,而大顶堆每次只能弹出最大值,我们无法移除其他数值,这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。**
此时我们需要一个队列,这个队列呢,放进去窗口里的元素,然后随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值是什么。
这个队列应该长这个样子:
```cpp
class MyQueue {
public:
void pop(int value) {
}
void push(int value) {
}
int front() {
return que.front();
}
};
```
每次窗口移动的时候,调用que.pop(滑动窗口中移除元素的数值),que.push(滑动窗口添加元素的数值),然后que.front()就返回我们要的最大值。
这么个队列香不香,要是有现成的这种数据结构是不是更香了!
其实在C++中,可以使用 multiset 来模拟这个过程,文末提供这个解法仅针对C++,以下讲解我们还是靠自己来实现这个单调队列。
然后再分析一下,队列里的元素一定是要排序的,而且要最大值放在出队口,要不然怎么知道最大值呢。
但如果把窗口里的元素都放进队列里,窗口移动的时候,队列需要弹出元素。
那么问题来了,已经排序之后的队列 怎么能把窗口要移除的元素(这个元素可不一定是最大值)弹出呢。
大家此时应该陷入深思.....
**其实队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。**
那么这个维护元素单调递减的队列就叫做**单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来实现一个单调队列**
**不要以为实现的单调队列就是 对窗口里面的数进行排序,如果排序的话,那和优先级队列又有什么区别了呢。**
来看一下单调队列如何维护队列里的元素。
动画如下:
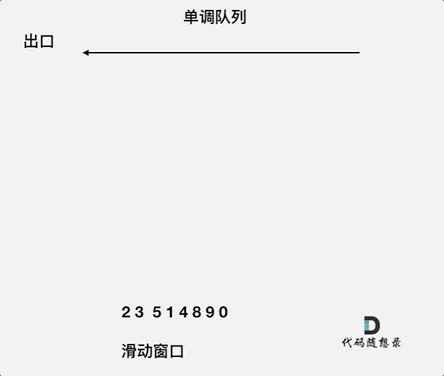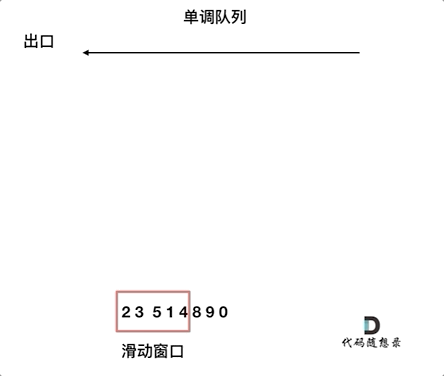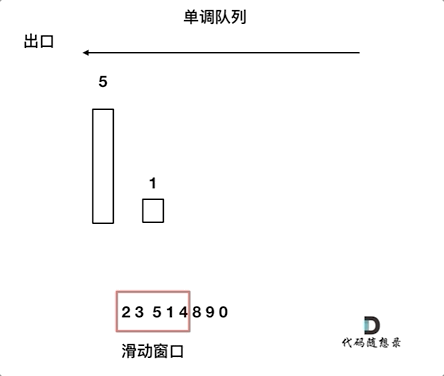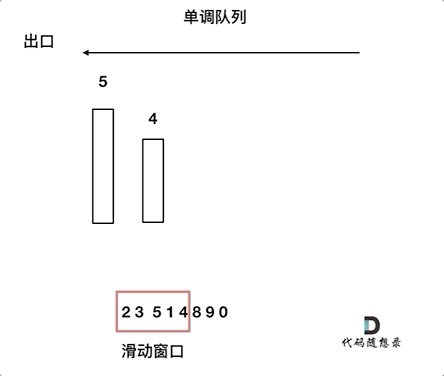
对于窗口里的元素{2, 3, 5, 1 ,4},单调队列里只维护{5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢?
设计单调队列的时候,pop,和push操作要保持如下规则:
1. pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
2. push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
为了更直观的感受到单调队列的工作过程,以题目示例为例,输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3,动画如下:
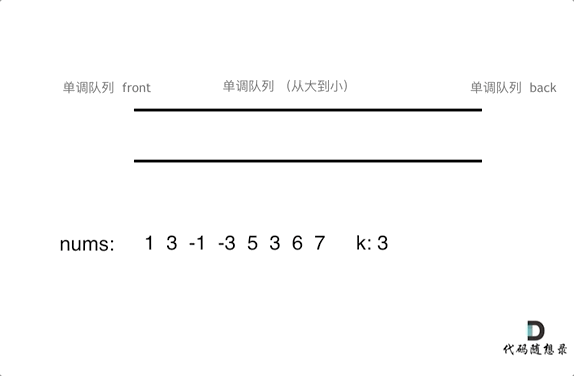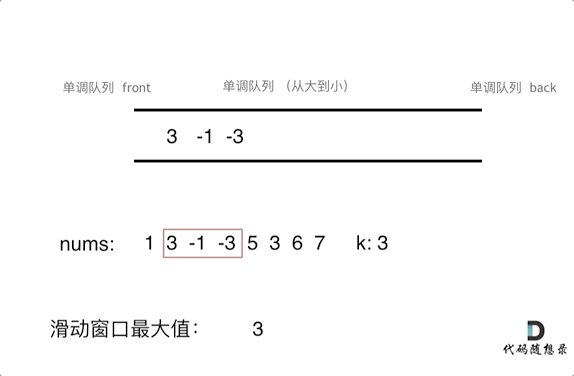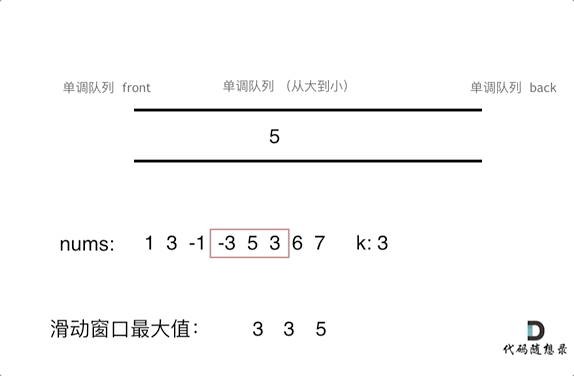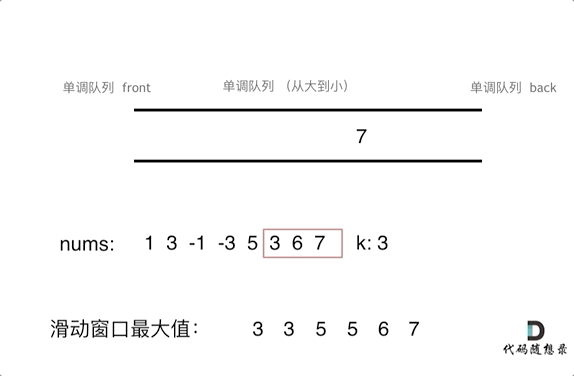
那么我们用什么数据结构来实现这个单调队列呢?
使用deque最为合适,在文章[栈与队列:来看看栈和队列不为人知的一面](https://programmercarl.com/栈与队列理论基础.html)中,我们就提到了常用的queue在没有指定容器的情况下,deque就是默认底层容器。
基于刚刚说过的单调队列pop和push的规则,代码不难实现,如下:
```CPP
class MyQueue { //单调队列(从大到小)
public:
deque que; // 使用deque来实现单调队列
// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
// 同时pop之前判断队列当前是否为空。
void pop(int value) {
if (!que.empty() && value == que.front()) {
que.pop_front();
}
}
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
// 这样就保持了队列里的数值是单调从大到小的了。
void push(int value) {
while (!que.empty() && value > que.back()) {
que.pop_back();
}
que.push_back(value);
}
// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
int front() {
return que.front();
}
};
```
这样我们就用deque实现了一个单调队列,接下来解决滑动窗口最大值的问题就很简单了,直接看代码吧。
C++代码如下:
```CPP
class Solution {
private:
class MyQueue { //单调队列(从大到小)
public:
deque que; // 使用deque来实现单调队列
// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
// 同时pop之前判断队列当前是否为空。
void pop(int value) {
if (!que.empty() && value == que.front()) {
que.pop_front();
}
}
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
// 这样就保持了队列里的数值是单调从大到小的了。
void push(int value) {
while (!que.empty() && value > que.back()) {
que.pop_back();
}
que.push_back(value);
}
// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
int front() {
return que.front();
}
};
public:
vector maxSlidingWindow(vector& nums, int k) {
MyQueue que;
vector result;
for (int i = 0; i < k; i++) { // 先将前k的元素放进队列
que.push(nums[i]);
}
result.push_back(que.front()); // result 记录前k的元素的最大值
for (int i = k; i < nums.size(); i++) {
que.pop(nums[i - k]); // 滑动窗口移除最前面元素
que.push(nums[i]); // 滑动窗口前加入最后面的元素
result.push_back(que.front()); // 记录对应的最大值
}
return result;
}
};
```
* 时间复杂度: O(n)
* 空间复杂度: O(k)
再来看一下时间复杂度,使用单调队列的时间复杂度是 O(n)。
有的同学可能想了,在队列中 push元素的过程中,还有pop操作呢,感觉不是纯粹的O(n)。
其实,大家可以自己观察一下单调队列的实现,nums 中的每个元素最多也就被 push_back 和 pop_back 各一次,没有任何多余操作,所以整体的复杂度还是 O(n)。
空间复杂度因为我们定义一个辅助队列,所以是O(k)。
## 扩展
大家貌似对单调队列 都有一些疑惑,首先要明确的是,题解中单调队列里的pop和push接口,仅适用于本题哈。单调队列不是一成不变的,而是不同场景不同写法,总之要保证队列里单调递减或递增的原则,所以叫做单调队列。 不要以为本题中的单调队列实现就是固定的写法哈。
大家貌似对deque也有一些疑惑,C++中deque是stack和queue默认的底层实现容器(这个我们之前已经讲过啦),deque是可以两边扩展的,而且deque里元素并不是严格的连续分布的。
## 其他语言版本
### Java:
```Java
//解法一
//自定义数组
class MyQueue {
Deque deque = new LinkedList<>();
//弹出元素时,比较当前要弹出的数值是否等于队列出口的数值,如果相等则弹出
//同时判断队列当前是否为空
void poll(int val) {
if (!deque.isEmpty() && val == deque.peek()) {
deque.poll();
}
}
//添加元素时,如果要添加的元素大于入口处的元素,就将入口元素弹出
//保证队列元素单调递减
//比如此时队列元素3,1,2将要入队,比1大,所以1弹出,此时队列:3,2
void add(int val) {
while (!deque.isEmpty() && val > deque.getLast()) {
deque.removeLast();
}
deque.add(val);
}
//队列队顶元素始终为最大值
int peek() {
return deque.peek();
}
}
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums.length == 1) {
return nums;
}
int len = nums.length - k + 1;
//存放结果元素的数组
int[] res = new int[len];
int num = 0;
//自定义队列
MyQueue myQueue = new MyQueue();
//先将前k的元素放入队列
for (int i = 0; i < k; i++) {
myQueue.add(nums[i]);
}
res[num++] = myQueue.peek();
for (int i = k; i < nums.length; i++) {
//滑动窗口移除最前面的元素,移除是判断该元素是否放入队列
myQueue.poll(nums[i - k]);
//滑动窗口加入最后面的元素
myQueue.add(nums[i]);
//记录对应的最大值
res[num++] = myQueue.peek();
}
return res;
}
}
//解法二
//利用双端队列手动实现单调队列
/**
* 用一个单调队列来存储对应的下标,每当窗口滑动的时候,直接取队列的头部指针对应的值放入结果集即可
* 单调递减队列类似 (head -->) 3 --> 2 --> 1 --> 0 (--> tail) (左边为头结点,元素存的是下标)
*/
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
ArrayDeque deque = new ArrayDeque<>();
int n = nums.length;
int[] res = new int[n - k + 1];
int idx = 0;
for(int i = 0; i < n; i++) {
// 根据题意,i为nums下标,是要在[i - k + 1, i] 中选到最大值,只需要保证两点
// 1.队列头结点需要在[i - k + 1, i]范围内,不符合则要弹出
while(!deque.isEmpty() && deque.peek() < i - k + 1){
deque.poll();
}
// 2.维护单调递减队列:新元素若大于队尾元素,则弹出队尾元素,直到满足单调性
while(!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
deque.pollLast();
}
deque.offer(i);
// 因为单调,当i增长到符合第一个k范围的时候,每滑动一步都将队列头节点放入结果就行了
if(i >= k - 1){
res[idx++] = nums[deque.peek()];
}
}
return res;
}
}
```
### Python:
#### 解法一:使用自定义的单调队列类
```python
from collections import deque
class MyQueue: #单调队列(从大到小
def __init__(self):
self.queue = deque() #这里需要使用deque实现单调队列,直接使用list会超时
#每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
#同时pop之前判断队列当前是否为空。
def pop(self, value):
if self.queue and value == self.queue[0]:
self.queue.popleft()#list.pop()时间复杂度为O(n),这里需要使用collections.deque()
#如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
#这样就保持了队列里的数值是单调从大到小的了。
def push(self, value):
while self.queue and value > self.queue[-1]:
self.queue.pop()
self.queue.append(value)
#查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
def front(self):
return self.queue[0]
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
que = MyQueue()
result = []
for i in range(k): #先将前k的元素放进队列
que.push(nums[i])
result.append(que.front()) #result 记录前k的元素的最大值
for i in range(k, len(nums)):
que.pop(nums[i - k]) #滑动窗口移除最前面元素
que.push(nums[i]) #滑动窗口前加入最后面的元素
result.append(que.front()) #记录对应的最大值
return result
```
#### 解法二:直接用单调队列
```python
from collections import deque
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
max_list = [] # 结果集合
kept_nums = deque() # 单调队列
for i in range(len(nums)):
update_kept_nums(kept_nums, nums[i]) # 右侧新元素加入
if i >= k and nums[i - k] == kept_nums[0]: # 左侧旧元素如果等于单调队列头元素,需要移除头元素
kept_nums.popleft()
if i >= k - 1:
max_list.append(kept_nums[0])
return max_list
def update_kept_nums(kept_nums, num): # num 是新加入的元素
# 所有小于新元素的队列尾部元素,在新元素出现后,都是没有价值的,都需要被移除
while kept_nums and num > kept_nums[-1]:
kept_nums.pop()
kept_nums.append(num)
```
### Go:
```go
// 封装单调队列的方式解题
type MyQueue struct {
queue []int
}
func NewMyQueue() *MyQueue {
return &MyQueue{
queue: make([]int, 0),
}
}
func (m *MyQueue) Front() int {
return m.queue[0]
}
func (m *MyQueue) Back() int {
return m.queue[len(m.queue)-1]
}
func (m *MyQueue) Empty() bool {
return len(m.queue) == 0
}
func (m *MyQueue) Push(val int) {
for !m.Empty() && val > m.Back() {
m.queue = m.queue[:len(m.queue)-1]
}
m.queue = append(m.queue, val)
}
func (m *MyQueue) Pop(val int) {
if !m.Empty() && val == m.Front() {
m.queue = m.queue[1:]
}
}
func maxSlidingWindow(nums []int, k int) []int {
queue := NewMyQueue()
length := len(nums)
res := make([]int, 0)
// 先将前k个元素放入队列
for i := 0; i < k; i++ {
queue.Push(nums[i])
}
// 记录前k个元素的最大值
res = append(res, queue.Front())
for i := k; i < length; i++ {
// 滑动窗口移除最前面的元素
queue.Pop(nums[i-k])
// 滑动窗口添加最后面的元素
queue.Push(nums[i])
// 记录最大值
res = append(res, queue.Front())
}
return res
}
```
### JavaScript:
```javascript
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
var maxSlidingWindow = function (nums, k) {
class MonoQueue {
queue;
constructor() {
this.queue = [];
}
enqueue(value) {
let back = this.queue[this.queue.length - 1];
while (back !== undefined && back < value) {
this.queue.pop();
back = this.queue[this.queue.length - 1];
}
this.queue.push(value);
}
dequeue(value) {
let front = this.front();
if (front === value) {
this.queue.shift();
}
}
front() {
return this.queue[0];
}
}
let helperQueue = new MonoQueue();
let i = 0, j = 0;
let resArr = [];
while (j < k) {
helperQueue.enqueue(nums[j++]);
}
resArr.push(helperQueue.front());
while (j < nums.length) {
helperQueue.enqueue(nums[j]);
helperQueue.dequeue(nums[i]);
resArr.push(helperQueue.front());
i++, j++;
}
return resArr;
};
```
### TypeScript:
```typescript
function maxSlidingWindow(nums: number[], k: number): number[] {
/** 单调递减队列 */
class MonoQueue {
private queue: number[];
constructor() {
this.queue = [];
};
/** 入队:value如果大于队尾元素,则将队尾元素删除,直至队尾元素大于value,或者队列为空 */
public enqueue(value: number): void {
let back: number | undefined = this.queue[this.queue.length - 1];
while (back !== undefined && back < value) {
this.queue.pop();
back = this.queue[this.queue.length - 1];
}
this.queue.push(value);
};
/** 出队:只有当队头元素等于value,才出队 */
public dequeue(value: number): void {
let top: number | undefined = this.top();
if (top !== undefined && top === value) {
this.queue.shift();
}
}
public top(): number | undefined {
return this.queue[0];
}
}
const helperQueue: MonoQueue = new MonoQueue();
let i: number = 0,
j: number = 0;
let resArr: number[] = [];
while (j < k) {
helperQueue.enqueue(nums[j++]);
}
resArr.push(helperQueue.top()!);
while (j < nums.length) {
helperQueue.enqueue(nums[j]);
helperQueue.dequeue(nums[i]);
resArr.push(helperQueue.top()!);
j++, i++;
}
return resArr;
};
```
### Swift:
解法一:
```Swift
/// 双向链表
class DoublyListNode {
var head: DoublyListNode?
var tail: DoublyListNode?
var next: DoublyListNode?
var pre: DoublyListNode?
var value: Int = 0
init(_ value: Int = 0) {
self.value = value
}
func isEmpty() -> Bool {
return self.head == nil
}
func first() -> Int? {
return self.head?.value
}
func last() -> Int? {
return self.tail?.value
}
func removeFirst() {
if isEmpty() {
return
}
let next = self.head!.next
self.head?.next = nil// 移除首节点
next?.pre = nil
self.head = next
}
func removeLast() {
if let tail = self.tail {
if let pre = tail.pre {
self.tail?.pre = nil
pre.next = nil
self.tail = pre
} else {
self.head = nil
self.tail = nil
}
}
}
func append(_ value: Int) {
let node = DoublyListNode(value)
if self.head != nil {
node.pre = self.tail
self.tail?.next = node
self.tail = node
} else {
self.head = node
self.tail = node
self.pre = nil
self.next = nil
}
}
}
// 单调队列, 从大到小
class MyQueue {
// var queue: [Int]!// 用数组会超时
var queue: DoublyListNode!
init() {
// queue = [Int]()
queue = DoublyListNode()
}
// 滑动窗口时弹出第一个元素, 如果相等再弹出
func pop(x: Int) {
if !queue.isEmpty() && front() == x {
queue.removeFirst()
}
}
// 滑动窗口时添加下一个元素, 移除队尾比 x 小的元素 始终保证队头 > 队尾
func push(x: Int) {
while !queue.isEmpty() && queue.last()! < x {
queue.removeLast()
}
queue.append(x)
}
// 此时队头就是滑动窗口最大值
func front() -> Int {
return queue.first() ?? -1
}
}
class Solution {
func maxSlidingWindow(_ nums: [Int], _ k: Int) -> [Int] {
// 存放结果
var res = [Int]()
let queue = MyQueue()
// 先将前K个元素放入队列
for i in 0 ..< k {
queue.push(x: nums[i])
}
// 添加当前队列最大值到结果数组
res.append(queue.front())
for i in k ..< nums.count {
// 滑动窗口移除最前面元素
queue.pop(x: nums[i - k])
// 滑动窗口添加下一个元素
queue.push(x: nums[i])
// 保存当前队列最大值
res.append(queue.front())
}
return res
}
}
```
Swift解法二:
```swift
func maxSlidingWindow(_ nums: [Int], _ k: Int) -> [Int] {
var result = [Int]()
var window = [Int]()
var right = 0, left = right - k + 1
while right < nums.count {
let value = nums[right]
// 因为窗口移动丢弃的左边数
if left > 0, left - 1 == window.first {
window.removeFirst()
}
// 保证末尾的是最大的
while !window.isEmpty, value > nums[window.last!] {
window.removeLast()
}
window.append(right)
if left >= 0 { // 窗口形成
result.append(nums[window.first!])
}
right += 1
left += 1
}
return result
}
```
### Scala:
```scala
import scala.collection.mutable.ArrayBuffer
object Solution {
def maxSlidingWindow(nums: Array[Int], k: Int): Array[Int] = {
var len = nums.length - k + 1 // 滑动窗口长度
var res: Array[Int] = new Array[Int](len) // 声明存储结果的数组
var index = 0 // 结果数组指针
val queue: MyQueue = new MyQueue // 自定义队列
// 将前k个添加到queue
for (i <- 0 until k) {
queue.add(nums(i))
}
res(index) = queue.peek // 第一个滑动窗口的最大值
index += 1
for (i <- k until nums.length) {
queue.poll(nums(i - k)) // 首先移除第i-k个元素
queue.add(nums(i)) // 添加当前数字到队列
res(index) = queue.peek() // 赋值
index+=1
}
// 最终返回res,return关键字可以省略
res
}
}
class MyQueue {
var queue = ArrayBuffer[Int]()
// 移除元素,如果传递进来的跟队头相等,那么移除
def poll(value: Int): Unit = {
if (!queue.isEmpty && queue.head == value) {
queue.remove(0)
}
}
// 添加元素,当队尾大于当前元素就删除
def add(value: Int): Unit = {
while (!queue.isEmpty && value > queue.last) {
queue.remove(queue.length - 1)
}
queue.append(value)
}
def peek(): Int = queue.head
}
```
### PHP:
```php
class Solution {
/**
* @param Integer[] $nums
* @param Integer $k
* @return Integer[]
*/
function maxSlidingWindow($nums, $k) {
$myQueue = new MyQueue();
// 先将前k的元素放进队列
for ($i = 0; $i < $k; $i++) {
$myQueue->push($nums[$i]);
}
$result = [];
$result[] = $myQueue->max(); // result 记录前k的元素的最大值
for ($i = $k; $i < count($nums); $i++) {
$myQueue->pop($nums[$i - $k]); // 滑动窗口移除最前面元素
$myQueue->push($nums[$i]); // 滑动窗口前加入最后面的元素
$result[]= $myQueue->max(); // 记录对应的最大值
}
return $result;
}
}
// 单调对列构建
class MyQueue{
private $queue;
public function __construct(){
$this->queue = new SplQueue(); //底层是双向链表实现。
}
public function pop($v){
// 判断当前对列是否为空
// 比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
// bottom 从链表前端查看元素, dequeue 从双向链表的开头移动一个节点
if(!$this->queue->isEmpty() && $v == $this->queue->bottom()){
$this->queue->dequeue(); //弹出队列
}
}
public function push($v){
// 判断当前对列是否为空
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
// 这样就保持了队列里的数值是单调从大到小的了。
while (!$this->queue->isEmpty() && $v > $this->queue->top()) {
$this->queue->pop(); // pop从链表末尾弹出一个元素,
}
$this->queue->enqueue($v);
}
// 查询当前队列里的最大值 直接返回队首
public function max(){
// bottom 从链表前端查看元素, top从链表末尾查看元素
return $this->queue->bottom();
}
// 辅助理解: 打印队列元素
public function println(){
// "迭代器移动到链表头部": 可理解为从头遍历链表元素做准备。
// 【PHP中没有指针概念,所以就没说指针。从数据结构上理解,就是把指针指向链表头部】
$this->queue->rewind();
echo "Println: ";
while($this->queue->valid()){
echo $this->queue->current()," -> ";
$this->queue->next();
}
echo "\n";
}
}
```
### C#:
```csharp
class myDequeue{
private LinkedList linkedList = new LinkedList();
public void Enqueue(int n){
while(linkedList.Count > 0 && linkedList.Last.Value < n){
linkedList.RemoveLast();
}
linkedList.AddLast(n);
}
public int Max(){
return linkedList.First.Value;
}
public void Dequeue(int n){
if(linkedList.First.Value == n){
linkedList.RemoveFirst();
}
}
}
myDequeue window = new myDequeue();
List res = new List();
public int[] MaxSlidingWindow(int[] nums, int k) {
for(int i = 0; i < k; i++){
window.Enqueue(nums[i]);
}
res.Add(window.Max());
for(int i = k; i < nums.Length; i++){
window.Dequeue(nums[i-k]);
window.Enqueue(nums[i]);
res.Add(window.Max());
}
return res.ToArray();
}
```
### Rust:
```rust
impl Solution {
pub fn max_sliding_window(nums: Vec, k: i32) -> Vec {
let mut res = vec![];
let mut queue = VecDeque::with_capacity(k as usize);
for (i, &v) in nums.iter().enumerate() {
// 如果队列长度超过 k,那么需要移除队首过期元素
if i - queue.front().unwrap_or(&0) == k as usize {
queue.pop_front();
}
while let Some(&index) = queue.back() {
if nums[index] >= v {
break;
}
// 如果队列第一个元素比当前元素小,那么就把队列第一个元素弹出
queue.pop_back();
}
queue.push_back(i);
if i >= k as usize - 1 {
res.push(nums[queue[0]]);
}
}
res
}
}
```
### C++
使用multiset作为单调队列
多重集合(`multiset`) 用以有序地存储元素的容器。允许存在相等的元素。
在遍历原数组的时候,只需要把窗口的头元素加入到multiset中,然后把窗口的尾元素删除即可。因为multiset是有序的,并且提供了*rbegin(),可以直接获取窗口最大值。
```cpp
class Solution {
public:
vector maxSlidingWindow(vector& nums, int k) {
multiset st;
vector ans;
for (int i = 0; i < nums.size(); i++) {
if (i >= k) st.erase(st.find(nums[i - k]));
st.insert(nums[i]);
if (i >= k - 1) ans.push_back(*st.rbegin());
}
return ans;
}
};
```
### C
```c
int* maxSlidingWindow(int* nums, int numsSize, int k, int* returnSize) {
*returnSize = numsSize - k + 1;
int *res = (int*)malloc((*returnSize) * sizeof(int));
assert(res);
int *deque = (int*)malloc(numsSize * sizeof(int));
assert(deque);
int front = 0, rear = 0, idx = 0;
for (int i = 0 ; i < numsSize ; i++) {
while (front < rear && deque[front] <= i - k) {
front++;
}
while (front < rear && nums[deque[rear - 1]] <= nums[i]) {
rear--;
}
deque[rear++] = i;
if (i >= k - 1) {
res[idx++] = nums[deque[front]];
}
}
return res;
}
```
提示:
* 1 <= nums.length <= 10^5
* -10^4 <= nums[i] <= 10^4
* 1 <= k <= nums.length
## 算法公开课
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[单调队列正式登场!| LeetCode:239. 滑动窗口最大值](https://www.bilibili.com/video/BV1XS4y1p7qj),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
这是使用单调队列的经典题目。
难点是如何求一个区间里的最大值呢? (这好像是废话),暴力一下不就得了。
暴力方法,遍历一遍的过程中每次从窗口中再找到最大的数值,这样很明显是O(n × k)的算法。
有的同学可能会想用一个大顶堆(优先级队列)来存放这个窗口里的k个数字,这样就可以知道最大的最大值是多少了, **但是问题是这个窗口是移动的,而大顶堆每次只能弹出最大值,我们无法移除其他数值,这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。**
此时我们需要一个队列,这个队列呢,放进去窗口里的元素,然后随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值是什么。
这个队列应该长这个样子:
```cpp
class MyQueue {
public:
void pop(int value) {
}
void push(int value) {
}
int front() {
return que.front();
}
};
```
每次窗口移动的时候,调用que.pop(滑动窗口中移除元素的数值),que.push(滑动窗口添加元素的数值),然后que.front()就返回我们要的最大值。
这么个队列香不香,要是有现成的这种数据结构是不是更香了!
其实在C++中,可以使用 multiset 来模拟这个过程,文末提供这个解法仅针对C++,以下讲解我们还是靠自己来实现这个单调队列。
然后再分析一下,队列里的元素一定是要排序的,而且要最大值放在出队口,要不然怎么知道最大值呢。
但如果把窗口里的元素都放进队列里,窗口移动的时候,队列需要弹出元素。
那么问题来了,已经排序之后的队列 怎么能把窗口要移除的元素(这个元素可不一定是最大值)弹出呢。
大家此时应该陷入深思.....
**其实队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。**
那么这个维护元素单调递减的队列就叫做**单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来实现一个单调队列**
**不要以为实现的单调队列就是 对窗口里面的数进行排序,如果排序的话,那和优先级队列又有什么区别了呢。**
来看一下单调队列如何维护队列里的元素。
动画如下:

对于窗口里的元素{2, 3, 5, 1 ,4},单调队列里只维护{5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢?
设计单调队列的时候,pop,和push操作要保持如下规则:
1. pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
2. push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
为了更直观的感受到单调队列的工作过程,以题目示例为例,输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3,动画如下:

那么我们用什么数据结构来实现这个单调队列呢?
使用deque最为合适,在文章[栈与队列:来看看栈和队列不为人知的一面](https://programmercarl.com/栈与队列理论基础.html)中,我们就提到了常用的queue在没有指定容器的情况下,deque就是默认底层容器。
基于刚刚说过的单调队列pop和push的规则,代码不难实现,如下:
```CPP
class MyQueue { //单调队列(从大到小)
public:
deque que; // 使用deque来实现单调队列
// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
// 同时pop之前判断队列当前是否为空。
void pop(int value) {
if (!que.empty() && value == que.front()) {
que.pop_front();
}
}
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
// 这样就保持了队列里的数值是单调从大到小的了。
void push(int value) {
while (!que.empty() && value > que.back()) {
que.pop_back();
}
que.push_back(value);
}
// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
int front() {
return que.front();
}
};
```
这样我们就用deque实现了一个单调队列,接下来解决滑动窗口最大值的问题就很简单了,直接看代码吧。
C++代码如下:
```CPP
class Solution {
private:
class MyQueue { //单调队列(从大到小)
public:
deque que; // 使用deque来实现单调队列
// 每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
// 同时pop之前判断队列当前是否为空。
void pop(int value) {
if (!que.empty() && value == que.front()) {
que.pop_front();
}
}
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
// 这样就保持了队列里的数值是单调从大到小的了。
void push(int value) {
while (!que.empty() && value > que.back()) {
que.pop_back();
}
que.push_back(value);
}
// 查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
int front() {
return que.front();
}
};
public:
vector maxSlidingWindow(vector& nums, int k) {
MyQueue que;
vector result;
for (int i = 0; i < k; i++) { // 先将前k的元素放进队列
que.push(nums[i]);
}
result.push_back(que.front()); // result 记录前k的元素的最大值
for (int i = k; i < nums.size(); i++) {
que.pop(nums[i - k]); // 滑动窗口移除最前面元素
que.push(nums[i]); // 滑动窗口前加入最后面的元素
result.push_back(que.front()); // 记录对应的最大值
}
return result;
}
};
```
* 时间复杂度: O(n)
* 空间复杂度: O(k)
再来看一下时间复杂度,使用单调队列的时间复杂度是 O(n)。
有的同学可能想了,在队列中 push元素的过程中,还有pop操作呢,感觉不是纯粹的O(n)。
其实,大家可以自己观察一下单调队列的实现,nums 中的每个元素最多也就被 push_back 和 pop_back 各一次,没有任何多余操作,所以整体的复杂度还是 O(n)。
空间复杂度因为我们定义一个辅助队列,所以是O(k)。
## 扩展
大家貌似对单调队列 都有一些疑惑,首先要明确的是,题解中单调队列里的pop和push接口,仅适用于本题哈。单调队列不是一成不变的,而是不同场景不同写法,总之要保证队列里单调递减或递增的原则,所以叫做单调队列。 不要以为本题中的单调队列实现就是固定的写法哈。
大家貌似对deque也有一些疑惑,C++中deque是stack和queue默认的底层实现容器(这个我们之前已经讲过啦),deque是可以两边扩展的,而且deque里元素并不是严格的连续分布的。
## 其他语言版本
### Java:
```Java
//解法一
//自定义数组
class MyQueue {
Deque deque = new LinkedList<>();
//弹出元素时,比较当前要弹出的数值是否等于队列出口的数值,如果相等则弹出
//同时判断队列当前是否为空
void poll(int val) {
if (!deque.isEmpty() && val == deque.peek()) {
deque.poll();
}
}
//添加元素时,如果要添加的元素大于入口处的元素,就将入口元素弹出
//保证队列元素单调递减
//比如此时队列元素3,1,2将要入队,比1大,所以1弹出,此时队列:3,2
void add(int val) {
while (!deque.isEmpty() && val > deque.getLast()) {
deque.removeLast();
}
deque.add(val);
}
//队列队顶元素始终为最大值
int peek() {
return deque.peek();
}
}
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if (nums.length == 1) {
return nums;
}
int len = nums.length - k + 1;
//存放结果元素的数组
int[] res = new int[len];
int num = 0;
//自定义队列
MyQueue myQueue = new MyQueue();
//先将前k的元素放入队列
for (int i = 0; i < k; i++) {
myQueue.add(nums[i]);
}
res[num++] = myQueue.peek();
for (int i = k; i < nums.length; i++) {
//滑动窗口移除最前面的元素,移除是判断该元素是否放入队列
myQueue.poll(nums[i - k]);
//滑动窗口加入最后面的元素
myQueue.add(nums[i]);
//记录对应的最大值
res[num++] = myQueue.peek();
}
return res;
}
}
//解法二
//利用双端队列手动实现单调队列
/**
* 用一个单调队列来存储对应的下标,每当窗口滑动的时候,直接取队列的头部指针对应的值放入结果集即可
* 单调递减队列类似 (head -->) 3 --> 2 --> 1 --> 0 (--> tail) (左边为头结点,元素存的是下标)
*/
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
ArrayDeque deque = new ArrayDeque<>();
int n = nums.length;
int[] res = new int[n - k + 1];
int idx = 0;
for(int i = 0; i < n; i++) {
// 根据题意,i为nums下标,是要在[i - k + 1, i] 中选到最大值,只需要保证两点
// 1.队列头结点需要在[i - k + 1, i]范围内,不符合则要弹出
while(!deque.isEmpty() && deque.peek() < i - k + 1){
deque.poll();
}
// 2.维护单调递减队列:新元素若大于队尾元素,则弹出队尾元素,直到满足单调性
while(!deque.isEmpty() && nums[deque.peekLast()] < nums[i]) {
deque.pollLast();
}
deque.offer(i);
// 因为单调,当i增长到符合第一个k范围的时候,每滑动一步都将队列头节点放入结果就行了
if(i >= k - 1){
res[idx++] = nums[deque.peek()];
}
}
return res;
}
}
```
### Python:
#### 解法一:使用自定义的单调队列类
```python
from collections import deque
class MyQueue: #单调队列(从大到小
def __init__(self):
self.queue = deque() #这里需要使用deque实现单调队列,直接使用list会超时
#每次弹出的时候,比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
#同时pop之前判断队列当前是否为空。
def pop(self, value):
if self.queue and value == self.queue[0]:
self.queue.popleft()#list.pop()时间复杂度为O(n),这里需要使用collections.deque()
#如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
#这样就保持了队列里的数值是单调从大到小的了。
def push(self, value):
while self.queue and value > self.queue[-1]:
self.queue.pop()
self.queue.append(value)
#查询当前队列里的最大值 直接返回队列前端也就是front就可以了。
def front(self):
return self.queue[0]
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
que = MyQueue()
result = []
for i in range(k): #先将前k的元素放进队列
que.push(nums[i])
result.append(que.front()) #result 记录前k的元素的最大值
for i in range(k, len(nums)):
que.pop(nums[i - k]) #滑动窗口移除最前面元素
que.push(nums[i]) #滑动窗口前加入最后面的元素
result.append(que.front()) #记录对应的最大值
return result
```
#### 解法二:直接用单调队列
```python
from collections import deque
class Solution:
def maxSlidingWindow(self, nums: List[int], k: int) -> List[int]:
max_list = [] # 结果集合
kept_nums = deque() # 单调队列
for i in range(len(nums)):
update_kept_nums(kept_nums, nums[i]) # 右侧新元素加入
if i >= k and nums[i - k] == kept_nums[0]: # 左侧旧元素如果等于单调队列头元素,需要移除头元素
kept_nums.popleft()
if i >= k - 1:
max_list.append(kept_nums[0])
return max_list
def update_kept_nums(kept_nums, num): # num 是新加入的元素
# 所有小于新元素的队列尾部元素,在新元素出现后,都是没有价值的,都需要被移除
while kept_nums and num > kept_nums[-1]:
kept_nums.pop()
kept_nums.append(num)
```
### Go:
```go
// 封装单调队列的方式解题
type MyQueue struct {
queue []int
}
func NewMyQueue() *MyQueue {
return &MyQueue{
queue: make([]int, 0),
}
}
func (m *MyQueue) Front() int {
return m.queue[0]
}
func (m *MyQueue) Back() int {
return m.queue[len(m.queue)-1]
}
func (m *MyQueue) Empty() bool {
return len(m.queue) == 0
}
func (m *MyQueue) Push(val int) {
for !m.Empty() && val > m.Back() {
m.queue = m.queue[:len(m.queue)-1]
}
m.queue = append(m.queue, val)
}
func (m *MyQueue) Pop(val int) {
if !m.Empty() && val == m.Front() {
m.queue = m.queue[1:]
}
}
func maxSlidingWindow(nums []int, k int) []int {
queue := NewMyQueue()
length := len(nums)
res := make([]int, 0)
// 先将前k个元素放入队列
for i := 0; i < k; i++ {
queue.Push(nums[i])
}
// 记录前k个元素的最大值
res = append(res, queue.Front())
for i := k; i < length; i++ {
// 滑动窗口移除最前面的元素
queue.Pop(nums[i-k])
// 滑动窗口添加最后面的元素
queue.Push(nums[i])
// 记录最大值
res = append(res, queue.Front())
}
return res
}
```
### JavaScript:
```javascript
/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
var maxSlidingWindow = function (nums, k) {
class MonoQueue {
queue;
constructor() {
this.queue = [];
}
enqueue(value) {
let back = this.queue[this.queue.length - 1];
while (back !== undefined && back < value) {
this.queue.pop();
back = this.queue[this.queue.length - 1];
}
this.queue.push(value);
}
dequeue(value) {
let front = this.front();
if (front === value) {
this.queue.shift();
}
}
front() {
return this.queue[0];
}
}
let helperQueue = new MonoQueue();
let i = 0, j = 0;
let resArr = [];
while (j < k) {
helperQueue.enqueue(nums[j++]);
}
resArr.push(helperQueue.front());
while (j < nums.length) {
helperQueue.enqueue(nums[j]);
helperQueue.dequeue(nums[i]);
resArr.push(helperQueue.front());
i++, j++;
}
return resArr;
};
```
### TypeScript:
```typescript
function maxSlidingWindow(nums: number[], k: number): number[] {
/** 单调递减队列 */
class MonoQueue {
private queue: number[];
constructor() {
this.queue = [];
};
/** 入队:value如果大于队尾元素,则将队尾元素删除,直至队尾元素大于value,或者队列为空 */
public enqueue(value: number): void {
let back: number | undefined = this.queue[this.queue.length - 1];
while (back !== undefined && back < value) {
this.queue.pop();
back = this.queue[this.queue.length - 1];
}
this.queue.push(value);
};
/** 出队:只有当队头元素等于value,才出队 */
public dequeue(value: number): void {
let top: number | undefined = this.top();
if (top !== undefined && top === value) {
this.queue.shift();
}
}
public top(): number | undefined {
return this.queue[0];
}
}
const helperQueue: MonoQueue = new MonoQueue();
let i: number = 0,
j: number = 0;
let resArr: number[] = [];
while (j < k) {
helperQueue.enqueue(nums[j++]);
}
resArr.push(helperQueue.top()!);
while (j < nums.length) {
helperQueue.enqueue(nums[j]);
helperQueue.dequeue(nums[i]);
resArr.push(helperQueue.top()!);
j++, i++;
}
return resArr;
};
```
### Swift:
解法一:
```Swift
/// 双向链表
class DoublyListNode {
var head: DoublyListNode?
var tail: DoublyListNode?
var next: DoublyListNode?
var pre: DoublyListNode?
var value: Int = 0
init(_ value: Int = 0) {
self.value = value
}
func isEmpty() -> Bool {
return self.head == nil
}
func first() -> Int? {
return self.head?.value
}
func last() -> Int? {
return self.tail?.value
}
func removeFirst() {
if isEmpty() {
return
}
let next = self.head!.next
self.head?.next = nil// 移除首节点
next?.pre = nil
self.head = next
}
func removeLast() {
if let tail = self.tail {
if let pre = tail.pre {
self.tail?.pre = nil
pre.next = nil
self.tail = pre
} else {
self.head = nil
self.tail = nil
}
}
}
func append(_ value: Int) {
let node = DoublyListNode(value)
if self.head != nil {
node.pre = self.tail
self.tail?.next = node
self.tail = node
} else {
self.head = node
self.tail = node
self.pre = nil
self.next = nil
}
}
}
// 单调队列, 从大到小
class MyQueue {
// var queue: [Int]!// 用数组会超时
var queue: DoublyListNode!
init() {
// queue = [Int]()
queue = DoublyListNode()
}
// 滑动窗口时弹出第一个元素, 如果相等再弹出
func pop(x: Int) {
if !queue.isEmpty() && front() == x {
queue.removeFirst()
}
}
// 滑动窗口时添加下一个元素, 移除队尾比 x 小的元素 始终保证队头 > 队尾
func push(x: Int) {
while !queue.isEmpty() && queue.last()! < x {
queue.removeLast()
}
queue.append(x)
}
// 此时队头就是滑动窗口最大值
func front() -> Int {
return queue.first() ?? -1
}
}
class Solution {
func maxSlidingWindow(_ nums: [Int], _ k: Int) -> [Int] {
// 存放结果
var res = [Int]()
let queue = MyQueue()
// 先将前K个元素放入队列
for i in 0 ..< k {
queue.push(x: nums[i])
}
// 添加当前队列最大值到结果数组
res.append(queue.front())
for i in k ..< nums.count {
// 滑动窗口移除最前面元素
queue.pop(x: nums[i - k])
// 滑动窗口添加下一个元素
queue.push(x: nums[i])
// 保存当前队列最大值
res.append(queue.front())
}
return res
}
}
```
Swift解法二:
```swift
func maxSlidingWindow(_ nums: [Int], _ k: Int) -> [Int] {
var result = [Int]()
var window = [Int]()
var right = 0, left = right - k + 1
while right < nums.count {
let value = nums[right]
// 因为窗口移动丢弃的左边数
if left > 0, left - 1 == window.first {
window.removeFirst()
}
// 保证末尾的是最大的
while !window.isEmpty, value > nums[window.last!] {
window.removeLast()
}
window.append(right)
if left >= 0 { // 窗口形成
result.append(nums[window.first!])
}
right += 1
left += 1
}
return result
}
```
### Scala:
```scala
import scala.collection.mutable.ArrayBuffer
object Solution {
def maxSlidingWindow(nums: Array[Int], k: Int): Array[Int] = {
var len = nums.length - k + 1 // 滑动窗口长度
var res: Array[Int] = new Array[Int](len) // 声明存储结果的数组
var index = 0 // 结果数组指针
val queue: MyQueue = new MyQueue // 自定义队列
// 将前k个添加到queue
for (i <- 0 until k) {
queue.add(nums(i))
}
res(index) = queue.peek // 第一个滑动窗口的最大值
index += 1
for (i <- k until nums.length) {
queue.poll(nums(i - k)) // 首先移除第i-k个元素
queue.add(nums(i)) // 添加当前数字到队列
res(index) = queue.peek() // 赋值
index+=1
}
// 最终返回res,return关键字可以省略
res
}
}
class MyQueue {
var queue = ArrayBuffer[Int]()
// 移除元素,如果传递进来的跟队头相等,那么移除
def poll(value: Int): Unit = {
if (!queue.isEmpty && queue.head == value) {
queue.remove(0)
}
}
// 添加元素,当队尾大于当前元素就删除
def add(value: Int): Unit = {
while (!queue.isEmpty && value > queue.last) {
queue.remove(queue.length - 1)
}
queue.append(value)
}
def peek(): Int = queue.head
}
```
### PHP:
```php
class Solution {
/**
* @param Integer[] $nums
* @param Integer $k
* @return Integer[]
*/
function maxSlidingWindow($nums, $k) {
$myQueue = new MyQueue();
// 先将前k的元素放进队列
for ($i = 0; $i < $k; $i++) {
$myQueue->push($nums[$i]);
}
$result = [];
$result[] = $myQueue->max(); // result 记录前k的元素的最大值
for ($i = $k; $i < count($nums); $i++) {
$myQueue->pop($nums[$i - $k]); // 滑动窗口移除最前面元素
$myQueue->push($nums[$i]); // 滑动窗口前加入最后面的元素
$result[]= $myQueue->max(); // 记录对应的最大值
}
return $result;
}
}
// 单调对列构建
class MyQueue{
private $queue;
public function __construct(){
$this->queue = new SplQueue(); //底层是双向链表实现。
}
public function pop($v){
// 判断当前对列是否为空
// 比较当前要弹出的数值是否等于队列出口元素的数值,如果相等则弹出。
// bottom 从链表前端查看元素, dequeue 从双向链表的开头移动一个节点
if(!$this->queue->isEmpty() && $v == $this->queue->bottom()){
$this->queue->dequeue(); //弹出队列
}
}
public function push($v){
// 判断当前对列是否为空
// 如果push的数值大于入口元素的数值,那么就将队列后端的数值弹出,直到push的数值小于等于队列入口元素的数值为止。
// 这样就保持了队列里的数值是单调从大到小的了。
while (!$this->queue->isEmpty() && $v > $this->queue->top()) {
$this->queue->pop(); // pop从链表末尾弹出一个元素,
}
$this->queue->enqueue($v);
}
// 查询当前队列里的最大值 直接返回队首
public function max(){
// bottom 从链表前端查看元素, top从链表末尾查看元素
return $this->queue->bottom();
}
// 辅助理解: 打印队列元素
public function println(){
// "迭代器移动到链表头部": 可理解为从头遍历链表元素做准备。
// 【PHP中没有指针概念,所以就没说指针。从数据结构上理解,就是把指针指向链表头部】
$this->queue->rewind();
echo "Println: ";
while($this->queue->valid()){
echo $this->queue->current()," -> ";
$this->queue->next();
}
echo "\n";
}
}
```
### C#:
```csharp
class myDequeue{
private LinkedList linkedList = new LinkedList();
public void Enqueue(int n){
while(linkedList.Count > 0 && linkedList.Last.Value < n){
linkedList.RemoveLast();
}
linkedList.AddLast(n);
}
public int Max(){
return linkedList.First.Value;
}
public void Dequeue(int n){
if(linkedList.First.Value == n){
linkedList.RemoveFirst();
}
}
}
myDequeue window = new myDequeue();
List res = new List();
public int[] MaxSlidingWindow(int[] nums, int k) {
for(int i = 0; i < k; i++){
window.Enqueue(nums[i]);
}
res.Add(window.Max());
for(int i = k; i < nums.Length; i++){
window.Dequeue(nums[i-k]);
window.Enqueue(nums[i]);
res.Add(window.Max());
}
return res.ToArray();
}
```
### Rust:
```rust
impl Solution {
pub fn max_sliding_window(nums: Vec, k: i32) -> Vec {
let mut res = vec![];
let mut queue = VecDeque::with_capacity(k as usize);
for (i, &v) in nums.iter().enumerate() {
// 如果队列长度超过 k,那么需要移除队首过期元素
if i - queue.front().unwrap_or(&0) == k as usize {
queue.pop_front();
}
while let Some(&index) = queue.back() {
if nums[index] >= v {
break;
}
// 如果队列第一个元素比当前元素小,那么就把队列第一个元素弹出
queue.pop_back();
}
queue.push_back(i);
if i >= k as usize - 1 {
res.push(nums[queue[0]]);
}
}
res
}
}
```
### C++
使用multiset作为单调队列
多重集合(`multiset`) 用以有序地存储元素的容器。允许存在相等的元素。
在遍历原数组的时候,只需要把窗口的头元素加入到multiset中,然后把窗口的尾元素删除即可。因为multiset是有序的,并且提供了*rbegin(),可以直接获取窗口最大值。
```cpp
class Solution {
public:
vector maxSlidingWindow(vector& nums, int k) {
multiset st;
vector ans;
for (int i = 0; i < nums.size(); i++) {
if (i >= k) st.erase(st.find(nums[i - k]));
st.insert(nums[i]);
if (i >= k - 1) ans.push_back(*st.rbegin());
}
return ans;
}
};
```
### C
```c
int* maxSlidingWindow(int* nums, int numsSize, int k, int* returnSize) {
*returnSize = numsSize - k + 1;
int *res = (int*)malloc((*returnSize) * sizeof(int));
assert(res);
int *deque = (int*)malloc(numsSize * sizeof(int));
assert(deque);
int front = 0, rear = 0, idx = 0;
for (int i = 0 ; i < numsSize ; i++) {
while (front < rear && deque[front] <= i - k) {
front++;
}
while (front < rear && nums[deque[rear - 1]] <= nums[i]) {
rear--;
}
deque[rear++] = i;
if (i >= k - 1) {
res[idx++] = nums[deque[front]];
}
}
return res;
}
```
 提示:
* 1 <= nums.length <= 10^5
* -10^4 <= nums[i] <= 10^4
* 1 <= k <= nums.length
## 算法公开课
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[单调队列正式登场!| LeetCode:239. 滑动窗口最大值](https://www.bilibili.com/video/BV1XS4y1p7qj),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
这是使用单调队列的经典题目。
难点是如何求一个区间里的最大值呢? (这好像是废话),暴力一下不就得了。
暴力方法,遍历一遍的过程中每次从窗口中再找到最大的数值,这样很明显是O(n × k)的算法。
有的同学可能会想用一个大顶堆(优先级队列)来存放这个窗口里的k个数字,这样就可以知道最大的最大值是多少了, **但是问题是这个窗口是移动的,而大顶堆每次只能弹出最大值,我们无法移除其他数值,这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。**
此时我们需要一个队列,这个队列呢,放进去窗口里的元素,然后随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值是什么。
这个队列应该长这个样子:
```cpp
class MyQueue {
public:
void pop(int value) {
}
void push(int value) {
}
int front() {
return que.front();
}
};
```
每次窗口移动的时候,调用que.pop(滑动窗口中移除元素的数值),que.push(滑动窗口添加元素的数值),然后que.front()就返回我们要的最大值。
这么个队列香不香,要是有现成的这种数据结构是不是更香了!
其实在C++中,可以使用 multiset 来模拟这个过程,文末提供这个解法仅针对C++,以下讲解我们还是靠自己来实现这个单调队列。
然后再分析一下,队列里的元素一定是要排序的,而且要最大值放在出队口,要不然怎么知道最大值呢。
但如果把窗口里的元素都放进队列里,窗口移动的时候,队列需要弹出元素。
那么问题来了,已经排序之后的队列 怎么能把窗口要移除的元素(这个元素可不一定是最大值)弹出呢。
大家此时应该陷入深思.....
**其实队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。**
那么这个维护元素单调递减的队列就叫做**单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来实现一个单调队列**
**不要以为实现的单调队列就是 对窗口里面的数进行排序,如果排序的话,那和优先级队列又有什么区别了呢。**
来看一下单调队列如何维护队列里的元素。
动画如下:

对于窗口里的元素{2, 3, 5, 1 ,4},单调队列里只维护{5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢?
设计单调队列的时候,pop,和push操作要保持如下规则:
1. pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
2. push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
为了更直观的感受到单调队列的工作过程,以题目示例为例,输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3,动画如下:

那么我们用什么数据结构来实现这个单调队列呢?
使用deque最为合适,在文章[栈与队列:来看看栈和队列不为人知的一面](https://programmercarl.com/栈与队列理论基础.html)中,我们就提到了常用的queue在没有指定容器的情况下,deque就是默认底层容器。
基于刚刚说过的单调队列pop和push的规则,代码不难实现,如下:
```CPP
class MyQueue { //单调队列(从大到小)
public:
deque
提示:
* 1 <= nums.length <= 10^5
* -10^4 <= nums[i] <= 10^4
* 1 <= k <= nums.length
## 算法公开课
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[单调队列正式登场!| LeetCode:239. 滑动窗口最大值](https://www.bilibili.com/video/BV1XS4y1p7qj),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
这是使用单调队列的经典题目。
难点是如何求一个区间里的最大值呢? (这好像是废话),暴力一下不就得了。
暴力方法,遍历一遍的过程中每次从窗口中再找到最大的数值,这样很明显是O(n × k)的算法。
有的同学可能会想用一个大顶堆(优先级队列)来存放这个窗口里的k个数字,这样就可以知道最大的最大值是多少了, **但是问题是这个窗口是移动的,而大顶堆每次只能弹出最大值,我们无法移除其他数值,这样就造成大顶堆维护的不是滑动窗口里面的数值了。所以不能用大顶堆。**
此时我们需要一个队列,这个队列呢,放进去窗口里的元素,然后随着窗口的移动,队列也一进一出,每次移动之后,队列告诉我们里面的最大值是什么。
这个队列应该长这个样子:
```cpp
class MyQueue {
public:
void pop(int value) {
}
void push(int value) {
}
int front() {
return que.front();
}
};
```
每次窗口移动的时候,调用que.pop(滑动窗口中移除元素的数值),que.push(滑动窗口添加元素的数值),然后que.front()就返回我们要的最大值。
这么个队列香不香,要是有现成的这种数据结构是不是更香了!
其实在C++中,可以使用 multiset 来模拟这个过程,文末提供这个解法仅针对C++,以下讲解我们还是靠自己来实现这个单调队列。
然后再分析一下,队列里的元素一定是要排序的,而且要最大值放在出队口,要不然怎么知道最大值呢。
但如果把窗口里的元素都放进队列里,窗口移动的时候,队列需要弹出元素。
那么问题来了,已经排序之后的队列 怎么能把窗口要移除的元素(这个元素可不一定是最大值)弹出呢。
大家此时应该陷入深思.....
**其实队列没有必要维护窗口里的所有元素,只需要维护有可能成为窗口里最大值的元素就可以了,同时保证队列里的元素数值是由大到小的。**
那么这个维护元素单调递减的队列就叫做**单调队列,即单调递减或单调递增的队列。C++中没有直接支持单调队列,需要我们自己来实现一个单调队列**
**不要以为实现的单调队列就是 对窗口里面的数进行排序,如果排序的话,那和优先级队列又有什么区别了呢。**
来看一下单调队列如何维护队列里的元素。
动画如下:

对于窗口里的元素{2, 3, 5, 1 ,4},单调队列里只维护{5, 4} 就够了,保持单调队列里单调递减,此时队列出口元素就是窗口里最大元素。
此时大家应该怀疑单调队列里维护着{5, 4} 怎么配合窗口进行滑动呢?
设计单调队列的时候,pop,和push操作要保持如下规则:
1. pop(value):如果窗口移除的元素value等于单调队列的出口元素,那么队列弹出元素,否则不用任何操作
2. push(value):如果push的元素value大于入口元素的数值,那么就将队列入口的元素弹出,直到push元素的数值小于等于队列入口元素的数值为止
保持如上规则,每次窗口移动的时候,只要问que.front()就可以返回当前窗口的最大值。
为了更直观的感受到单调队列的工作过程,以题目示例为例,输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3,动画如下:

那么我们用什么数据结构来实现这个单调队列呢?
使用deque最为合适,在文章[栈与队列:来看看栈和队列不为人知的一面](https://programmercarl.com/栈与队列理论基础.html)中,我们就提到了常用的queue在没有指定容器的情况下,deque就是默认底层容器。
基于刚刚说过的单调队列pop和push的规则,代码不难实现,如下:
```CPP
class MyQueue { //单调队列(从大到小)
public:
deque