
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!
## 53. 最大子序和
[力扣题目链接](https://leetcode-cn.com/problems/maximum-subarray/)
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4]
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
## 思路
这道题之前我们在讲解贪心专题的时候用贪心算法解决过一次,[贪心算法:最大子序和](https://programmercarl.com/0053.最大子序和.html)。
这次我们用动态规划的思路再来分析一次。
动规五部曲如下:
1. 确定dp数组(dp table)以及下标的含义
**dp[i]:包括下标i之前的最大连续子序列和为dp[i]**。
2. 确定递推公式
dp[i]只有两个方向可以推出来:
* dp[i - 1] + nums[i],即:nums[i]加入当前连续子序列和
* nums[i],即:从头开始计算当前连续子序列和
一定是取最大的,所以dp[i] = max(dp[i - 1] + nums[i], nums[i]);
3. dp数组如何初始化
从递推公式可以看出来dp[i]是依赖于dp[i - 1]的状态,dp[0]就是递推公式的基础。
dp[0]应该是多少呢?
根据dp[i]的定义,很明显dp[0]应为nums[0]即dp[0] = nums[0]。
4. 确定遍历顺序
递推公式中dp[i]依赖于dp[i - 1]的状态,需要从前向后遍历。
5. 举例推导dp数组
以示例一为例,输入:nums = [-2,1,-3,4,-1,2,1,-5,4],对应的dp状态如下:
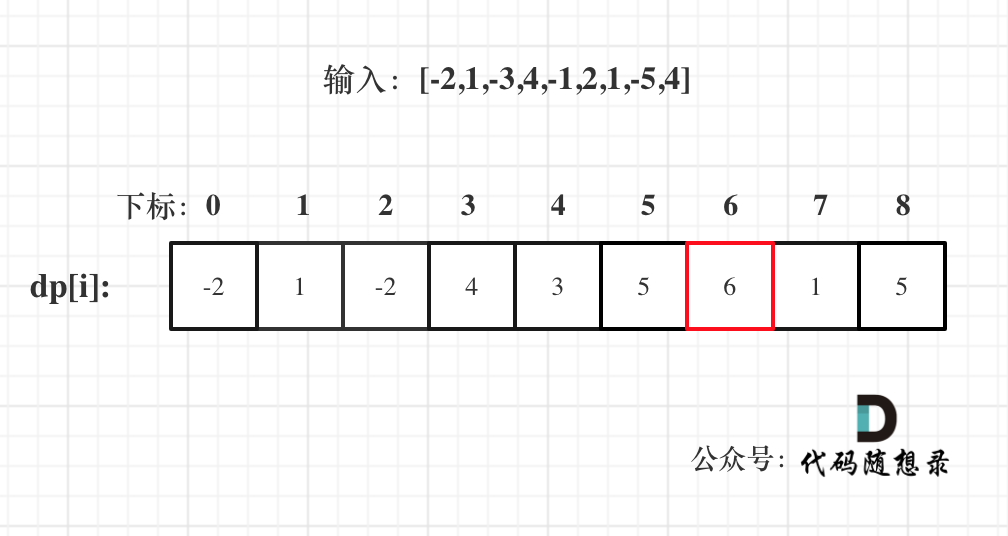
**注意最后的结果可不是dp[nums.size() - 1]!** ,而是dp[6]。
在回顾一下dp[i]的定义:包括下标i之前的最大连续子序列和为dp[i]。
那么我们要找最大的连续子序列,就应该找每一个i为终点的连续最大子序列。
所以在递推公式的时候,可以直接选出最大的dp[i]。
以上动规五部曲分析完毕,完整代码如下:
```CPP
class Solution {
public:
int maxSubArray(vector& nums) {
if (nums.size() == 0) return 0;
vector dp(nums.size());
dp[0] = nums[0];
int result = dp[0];
for (int i = 1; i < nums.size(); i++) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
}
return result;
}
};
```
* 时间复杂度:O(n)
* 空间复杂度:O(n)
## 总结
这道题目用贪心也很巧妙,但有一点绕,需要仔细想一想,如果想回顾一下贪心就看这里吧:[贪心算法:最大子序和](https://programmercarl.com/0053.最大子序和.html)
动规的解法还是很直接的。
## 其他语言版本
Java:
```java
/**
* 1.dp[i]代表当前下标对应的最大值
* 2.递推公式 dp[i] = max (dp[i-1]+nums[i],nums[i]) res = max(res,dp[i])
* 3.初始化 都为 0
* 4.遍历方向,从前往后
* 5.举例推导结果。。。
*
* @param nums
* @return
*/
public static int maxSubArray(int[] nums) {
if (nums.length == 0) {
return 0;
}
int res = nums[0];
int[] dp = new int[nums.length];
dp[0] = nums[0];
for (int i = 1; i < nums.length; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
res = res > dp[i] ? res : dp[i];
}
return res;
}
```
Python:
```python
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
dp = [0] * len(nums)
dp[0] = nums[0]
result = dp[0]
for i in range(1, len(nums)):
dp[i] = max(dp[i-1] + nums[i], nums[i]) #状态转移公式
result = max(result, dp[i]) #result 保存dp[i]的最大值
return result
```
Go:
```Go
// solution
// 1, dp
// 2, 贪心
func maxSubArray(nums []int) int {
n := len(nums)
// 这里的dp[i] 表示,最大的连续子数组和,包含num[i] 元素
dp := make([]int,n)
// 初始化,由于dp 状态转移方程依赖dp[0]
dp[0] = nums[0]
// 初始化最大的和
mx := nums[0]
for i:=1;ib {
return a
}
return b
}
```
JavaScript:
```javascript
const maxSubArray = nums => {
// 数组长度,dp初始化
const len = nums.length;
let dp = new Array(len).fill(0);
dp[0] = nums[0];
// 最大值初始化为dp[0]
let max = dp[0];
for (let i = 1; i < len; i++) {
dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
// 更新最大值
max = Math.max(max, dp[i]);
}
return max;
};
```
-----------------------

