参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

# 700.二叉搜索树中的搜索 [力扣题目地址](https://leetcode.cn/problems/search-in-a-binary-search-tree/) 给定二叉搜索树（BST）的根节点和一个值。你需要在BST中找到节点值等于给定值的节点。返回以该节点为根的子树。如果节点不存在，则返回 NULL。例如， ![700.二叉搜索树中的搜索](https://img-blog.csdnimg.cn/20210204155522476.png) 在上述示例中，如果要找的值是 5，但因为没有节点值为 5，我们应该返回 NULL。 # 思路之前我们讲了都是普通二叉树，那么接下来看看二叉搜索树。在[关于二叉树，你该了解这些！](https://programmercarl.com/二叉树理论基础.html)中，我们已经讲过了二叉搜索树。二叉搜索树是一个有序树： * 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值； * 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值； * 它的左、右子树也分别为二叉搜索树这就决定了，二叉搜索树，递归遍历和迭代遍历和普通二叉树都不一样。本题，其实就是在二叉搜索树中搜索一个节点。那么我们来看看应该如何遍历。 ## 递归法 1. 确定递归函数的参数和返回值递归函数的参数传入的就是根节点和要搜索的数值，返回的就是以这个搜索数值所在的节点。代码如下： ```CPP TreeNode* searchBST(TreeNode* root, int val) ``` 2. 确定终止条件如果root为空，或者找到这个数值了，就返回root节点。 ```CPP if (root == NULL || root->val == val) return root; ``` 3. 确定单层递归的逻辑看看二叉搜索树的单层递归逻辑有何不同。因为二叉搜索树的节点是有序的，所以可以有方向的去搜索。如果root->val > val，搜索左子树，如果root->val < val，就搜索右子树，最后如果都没有搜索到，就返回NULL。代码如下： ```CPP TreeNode* result = NULL; if (root->val > val) result = searchBST(root->left, val); if (root->val < val) result = searchBST(root->right, val); return result; ``` 很多录友写递归函数的时候习惯直接写 `searchBST(root->left, val)`，却忘了递归函数还有返回值。递归函数的返回值是什么? 是左子树如果搜索到了val，要将该节点返回。如果不用一个变量将其接住，那么返回值不就没了。所以要 `result = searchBST(root->left, val)`。整体代码如下： ```CPP class Solution { public: TreeNode* searchBST(TreeNode* root, int val) { if (root == NULL || root->val == val) return root; TreeNode* result = NULL; if (root->val > val) result = searchBST(root->left, val); if (root->val < val) result = searchBST(root->right, val); return result; } }; ``` 或者我们也可以这么写 ```CPP class Solution { public: TreeNode* searchBST(TreeNode* root, int val) { if (root == NULL || root->val == val) return root; if (root->val > val) return searchBST(root->left, val); if (root->val < val) return searchBST(root->right, val); return NULL; } }; ``` ## 迭代法一提到二叉树遍历的迭代法，可能立刻想起使用栈来模拟深度遍历，使用队列来模拟广度遍历。对于二叉搜索树可就不一样了，因为二叉搜索树的特殊性，也就是节点的有序性，可以不使用辅助栈或者队列就可以写出迭代法。对于一般二叉树，递归过程中还有回溯的过程，例如走一个左方向的分支走到头了，那么要调头，在走右分支。而**对于二叉搜索树，不需要回溯的过程，因为节点的有序性就帮我们确定了搜索的方向。** 例如要搜索元素为3的节点，**我们不需要搜索其他节点，也不需要做回溯，查找的路径已经规划好了。** 中间节点如果大于3就向左走，如果小于3就向右走，如图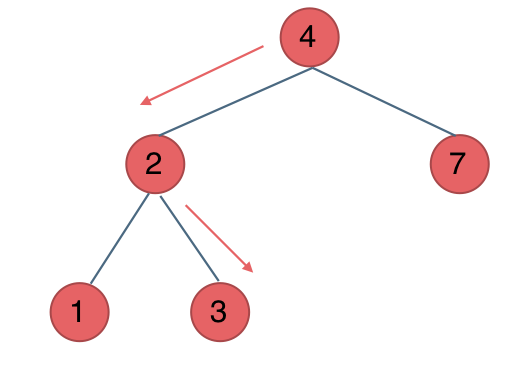： ![二叉搜索树](https://img-blog.csdnimg.cn/20200812190213280.png) 所以迭代法代码如下： ```CPP class Solution { public: TreeNode* searchBST(TreeNode* root, int val) { while (root != NULL) { if (root->val > val) root = root->left; else if (root->val < val) root = root->right; else return root; } return NULL; } }; ``` 第一次看到了如此简单的迭代法，是不是感动的痛哭流涕，哭一会~ # 总结本篇我们介绍了二叉搜索树的遍历方式，因为二叉搜索树的有序性，遍历的时候要比普通二叉树简单很多。但是一些同学很容易忽略二叉搜索树的特性，所以写出遍历的代码就未必真的简单了。所以针对二叉搜索树的题目，一样要利用其特性。文中我依然给出递归和迭代两种方式，可以看出写法都非常简单，就是利用了二叉搜索树有序的特点。 # 其他语言版本 ## Java ```Java class Solution { // 递归，普通二叉树 public TreeNode searchBST(TreeNode root, int val) { if (root == null || root.val == val) { return root; } TreeNode left = searchBST(root.left, val); if (left != null) { return left; } return searchBST(root.right, val); } } class Solution { // 递归，利用二叉搜索树特点，优化 public TreeNode searchBST(TreeNode root, int val) { if (root == null || root.val == val) { return root; } if (val < root.val) { return searchBST(root.left, val); } else { return searchBST(root.right, val); } } } class Solution { // 迭代，普通二叉树 public TreeNode searchBST(TreeNode root, int val) { if (root == null || root.val == val) { return root; } Stack stack = new Stack<>(); stack.push(root); while (!stack.isEmpty()) { TreeNode pop = stack.pop(); if (pop.val == val) { return pop; } if (pop.right != null) { stack.push(pop.right); } if (pop.left != null) { stack.push(pop.left); } } return null; } } class Solution { // 迭代，利用二叉搜索树特点，优化，可以不需要栈 public TreeNode searchBST(TreeNode root, int val) { while (root != null) if (val < root.val) root = root.left; else if (val > root.val) root = root.right; else return root; return null; } } ``` ## Python 递归法： ```python class Solution: def searchBST(self, root: TreeNode, val: int) -> TreeNode: # 为什么要有返回值: # 因为搜索到目标节点就要立即return， # 这样才是找到节点就返回（搜索某一条边），如果不加return，就是遍历整棵树了。 if not root or root.val == val: return root if root.val > val: return self.searchBST(root.left, val) if root.val < val: return self.searchBST(root.right, val) ``` 迭代法： ```python class Solution: def searchBST(self, root: TreeNode, val: int) -> TreeNode: while root is not None: if val < root.val: root = root.left elif val > root.val: root = root.right else: return root return None ``` ## Go 递归法： ```go //递归法 func searchBST(root *TreeNode, val int) *TreeNode { if root==nil||root.Val==val{ return root } if root.Val>val{ return searchBST(root.Left,val) } return searchBST(root.Right,val) } ``` 迭代法： ```go //迭代法 func searchBST(root *TreeNode, val int) *TreeNode { for root!=nil{ if root.Val>val{ root=root.Left }else if root.Val val) return searchBST(root.left, val); if (root.val < val) return searchBST(root.right, val); }; ``` 迭代： ```javascript /** * Definition for a binary tree node. * function TreeNode(val, left, right) { * this.val = (val===undefined ? 0 : val) * this.left = (left===undefined ? null : left) * this.right = (right===undefined ? null : right) * } */ /** * @param {TreeNode} root * @param {number} val * @return {TreeNode} */ var searchBST = function (root, val) { while (root !== null) { if (root.val > val) root = root.left; else if (root.val < val) root = root.right; else return root; } return null; }; ``` ## TypeScript > 递归法 ```typescript function searchBST(root: TreeNode | null, val: number): TreeNode | null { if (root === null || root.val === val) return root; if (root.val < val) return searchBST(root.right, val); if (root.val > val) return searchBST(root.left, val); return null; }; ``` > 迭代法 ```typescript function searchBST(root: TreeNode | null, val: number): TreeNode | null { let resNode: TreeNode | null = root; while (resNode !== null) { if (resNode.val === val) return resNode; if (resNode.val < val) { resNode = resNode.right; } else { resNode = resNode.left; } } return null; }; ``` ## Scala 递归: ```scala object Solution { def searchBST(root: TreeNode, value: Int): TreeNode = { if (root == null || value == root.value) return root // 相当于三元表达式，在Scala中if...else有返回值 if (value < root.value) searchBST(root.left, value) else searchBST(root.right, value) } } ``` 迭代: ```scala object Solution { def searchBST(root: TreeNode, value: Int): TreeNode = { // 因为root是不可变量，所以需要赋值给一个可变量 var node = root while (node != null) { if (value < node.value) node = node.left else if (value > node.value) node = node.right else return node } null // 没有返回就返回空 } } ``` -----------------------