参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# 105.有向图的完全可达性
[卡码网题目链接(ACM模式)](https://kamacoder.com/problempage.php?pid=1177)
【题目描述】
给定一个有向图,包含 N 个节点,节点编号分别为 1,2,...,N。现从 1 号节点开始,如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
【输入描述】
第一行包含两个正整数,表示节点数量 N 和边的数量 K。 后续 K 行,每行两个正整数 s 和 t,表示从 s 节点有一条边单向连接到 t 节点。
【输出描述】
如果可以从 1 号节点的边可以到达任何节点,则输出 1,否则输出 -1。
【输入示例】
```
4 4
1 2
2 1
1 3
2 4
```
【输出示例】
1
【提示信息】
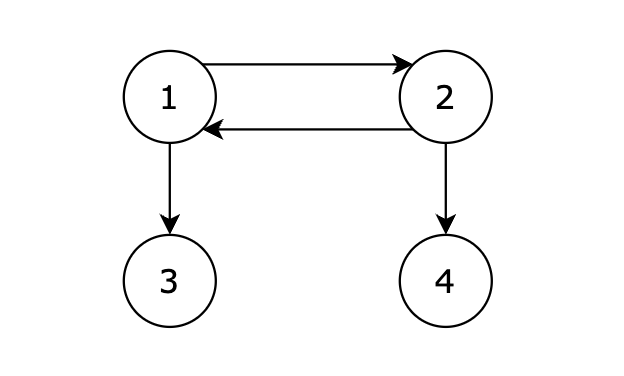
从 1 号节点可以到达任意节点,输出 1。
数据范围:
* 1 <= N <= 100;
* 1 <= K <= 2000。
## 思路
本题给我们是一个有向图, 意识到这是有向图很重要!
接下来我们再画一个图,从图里可以直观看出来,节点6 是 不能到达节点1 的
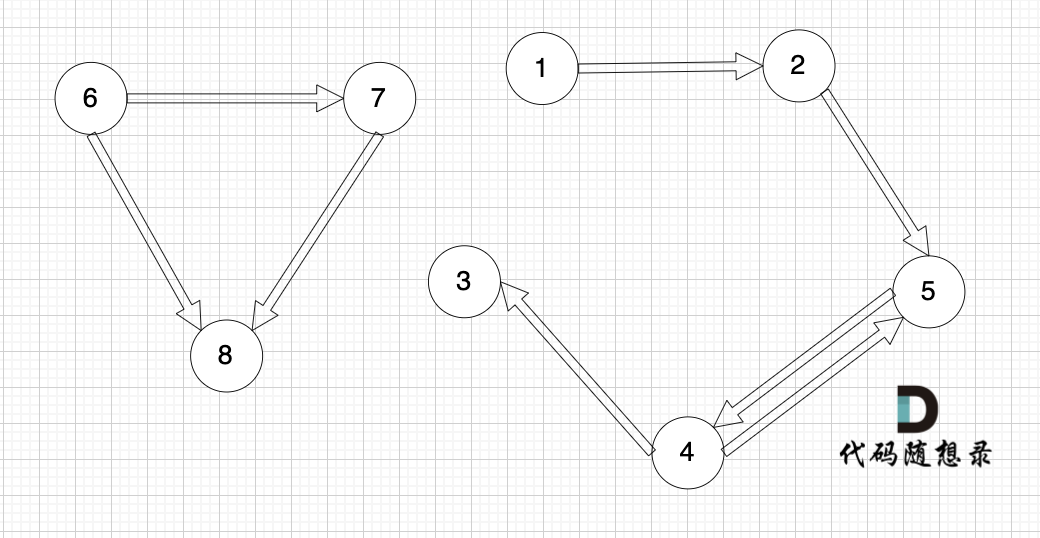
这就很容易让我们想起岛屿问题,只要发现独立的岛,就是不可到达的。
**但本题是有向图**,在有向图中,即使所有节点都是链接的,但依然不可能从0出发遍历所有边。
例如上图中,节点1 可以到达节点2,但节点2是不能到达节点1的。
所以本题是一个**有向图搜索全路径的问题**。 只能用深搜(DFS)或者广搜(BFS)来搜。
**以下dfs分析 大家一定要仔细看,本题有两种dfs的解法,很多题解没有讲清楚**。 看完之后 相信你对dfs会有更深的理解。
深搜三部曲:
1. 确认递归函数,参数
需要传入地图,需要知道当前我们拿到的key,以至于去下一个房间。
同时还需要一个数组,用来记录我们都走过了哪些房间,这样好知道最后有没有把所有房间都遍历的,可以定义一个一维数组。
所以 递归函数参数如下:
```C++
// key 当前得到的可以
// visited 记录访问过的房间
void dfs(const vector>& graph, int key, vector& visited) {
```
2. 确认终止条件
遍历的时候,什么时候终止呢?
这里有一个很重要的逻辑,就是在递归中,**我们是处理当前访问的节点,还是处理下一个要访问的节点**。
这决定 终止条件怎么写。
首先明确,本题中什么叫做处理,就是 visited数组来记录访问过的节点,该节点默认 数组里元素都是false,把元素标记为true就是处理 本节点了。
如果我们是处理当前访问的节点,当前访问的节点如果是 true ,说明是访问过的节点,那就终止本层递归,如果不是true,我们就把它赋值为true,因为这是我们处理本层递归的节点。
代码就是这样:
```C++
// 写法一:处理当前访问的节点
void dfs(const vector>& graph, int key, vector& visited) {
if (visited[key]) {
return;
}
visited[key] = true;
list keys = graph[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(graph, key, visited);
}
}
```
如果我们是处理下一层访问的节点,而不是当前层。那么就要在 深搜三部曲中第三步:处理目前搜索节点出发的路径的时候对 节点进行处理。
这样的话,就不需要终止条件,而是在 搜索下一个节点的时候,直接判断 下一个节点是否是我们要搜的节点。
代码就是这样的:
```C++
// 写法二:处理下一个要访问的节点
void dfs(const vector>& graph, int key, vector& visited) {
list keys = graph[key];
for (int key : keys) {
if (visited[key] == false) { // 确认下一个是没访问过的节点
visited[key] = true;
dfs(graph, key, visited);
}
}
}
```
可以看出,**如何看待 我们要访问的节点,直接决定了两种不一样的写法**,很多录友对这一块很模糊,可能做过这道题,但没有思考到这个维度上。
3. 处理目前搜索节点出发的路径
其实在上面,深搜三部曲 第二部,就已经讲了,因为终止条件的两种写法, 直接决定了两种不一样的递归写法。
这里还有细节:
看上面两个版本的写法中, 好像没有发现回溯的逻辑。
我们都知道,有递归就有回溯,回溯就在递归函数的下面, 那么之前我们做的dfs题目,都需要回溯操作,例如:[0098.所有可达路径](./0098.所有可达路径), **为什么本题就没有回溯呢?**
代码中可以看到dfs函数下面并没有回溯的操作。
此时就要在思考本题的要求了,本题是需要判断 1节点 是否能到所有节点,那么我们就没有必要回溯去撤销操作了,只要遍历过的节点一律都标记上。
**那什么时候需要回溯操作呢?**
当我们需要搜索一条可行路径的时候,就需要回溯操作了,因为没有回溯,就没法“调头”, 如果不理解的话,去看我写的 [0098.所有可达路径](./0098.所有可达路径.md) 的题解。
以上分析完毕,DFS整体实现C++代码如下:
```CPP
// 写法一:dfs 处理当前访问的节点
#include
#include
#include
using namespace std;
void dfs(const vector>& graph, int key, vector& visited) {
if (visited[key]) {
return;
}
visited[key] = true;
list keys = graph[key];
for (int key : keys) {
// 深度优先搜索遍历
dfs(graph, key, visited);
}
}
int main() {
int n, m, s, t;
cin >> n >> m;
// 节点编号从1到n,所以申请 n+1 这么大的数组
vector> graph(n + 1); // 邻接表
while (m--) {
cin >> s >> t;
// 使用邻接表 ,表示 s -> t 是相连的
graph[s].push_back(t);
}
vector visited(n + 1, false);
dfs(graph, 1, visited);
//检查是否都访问到了
for (int i = 1; i <= n; i++) {
if (visited[i] == false) {
cout << -1 << endl;
return 0;
}
}
cout << 1 << endl;
}
```
**第二种写法注意有注释的地方是和写法一的区别**
```CPP
写法二:dfs处理下一个要访问的节点
#include
#include
#include
using namespace std;
void dfs(const vector>& graph, int key, vector& visited) {
list keys = graph[key];
for (int key : keys) {
if (visited[key] == false) { // 确认下一个是没访问过的节点
visited[key] = true;
dfs(graph, key, visited);
}
}
}
int main() {
int n, m, s, t;
cin >> n >> m;
vector> graph(n + 1);
while (m--) {
cin >> s >> t;
graph[s].push_back(t);
}
vector visited(n + 1, false);
visited[1] = true; // 节点1 预先处理
dfs(graph, 1, visited);
for (int i = 1; i <= n; i++) {
if (visited[i] == false) {
cout << -1 << endl;
return 0;
}
}
cout << 1 << endl;
}
```
本题我也给出 BFS C++代码,[BFS理论基础](https://programmercarl.com/kamacoder/%E5%9B%BE%E8%AE%BA%E6%B7%B1%E6%90%9C%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html),代码如下:
```CPP
#include
#include
#include
#include
using namespace std;
int main() {
int n, m, s, t;
cin >> n >> m;
vector> graph(n + 1);
while (m--) {
cin >> s >> t;
graph[s].push_back(t);
}
vector visited(n + 1, false);
visited[1] = true; // 1 号房间开始
queue que;
que.push(1); // 1 号房间开始
// 广度优先搜索的过程
while (!que.empty()) {
int key = que.front(); que.pop();
list keys = graph[key];
for (int key : keys) {
if (!visited[key]) {
que.push(key);
visited[key] = true;
}
}
}
for (int i = 1; i <= n; i++) {
if (visited[i] == false) {
cout << -1 << endl;
return 0;
}
}
cout << 1 << endl;
}
```
## 其他语言版本
### Java
```java
import java.util.*;
public class Main {
public static List> adjList = new ArrayList<>();
public static void dfs(boolean[] visited, int key) {
if (visited[key]) {
return;
}
visited[key] = true;
List nextKeys = adjList.get(key);
for (int nextKey : nextKeys) {
dfs(visited, nextKey);
}
}
public static void bfs(boolean[] visited, int key) {
Queue queue = new LinkedList();
queue.add(key);
visited[key] = true;
while (!queue.isEmpty()) {
int curKey = queue.poll();
List list = adjList.get(curKey);
for (int nextKey : list) {
if (!visited[nextKey]) {
queue.add(nextKey);
visited[nextKey] = true;
}
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int vertices_num = sc.nextInt();
int line_num = sc.nextInt();
for (int i = 0; i < vertices_num; i++) {
adjList.add(new LinkedList<>());
}//Initialization
for (int i = 0; i < line_num; i++) {
int s = sc.nextInt();
int t = sc.nextInt();
adjList.get(s - 1).add(t - 1);
}//构造邻接表
boolean[] visited = new boolean[vertices_num];
dfs(visited, 0);
// bfs(visited, 0);
for (int i = 0; i < vertices_num; i++) {
if (!visited[i]) {
System.out.println(-1);
return;
}
}
System.out.println(1);
}
}
```
### Python
BFS算法
```Python
import collections
path = set() # 纪录 BFS 所经过之节点
def bfs(root, graph):
global path
que = collections.deque([root])
while que:
cur = que.popleft()
path.add(cur)
for nei in graph[cur]:
que.append(nei)
graph[cur] = []
return
def main():
N, K = map(int, input().strip().split())
graph = collections.defaultdict(list)
for _ in range(K):
src, dest = map(int, input().strip().split())
graph[src].append(dest)
bfs(1, graph)
if path == {i for i in range(1, N + 1)}:
return 1
return -1
if __name__ == "__main__":
print(main())
```
``` python
def dfs(graph, key, visited):
for neighbor in graph[key]:
if not visited[neighbor]: # Check if the next node is not visited
visited[neighbor] = True
dfs(graph, neighbor, visited)
def main():
import sys
input = sys.stdin.read
data = input().split()
n = int(data[0])
m = int(data[1])
graph = [[] for _ in range(n + 1)]
index = 2
for _ in range(m):
s = int(data[index])
t = int(data[index + 1])
graph[s].append(t)
index += 2
visited = [False] * (n + 1)
visited[1] = True # Process node 1 beforehand
dfs(graph, 1, visited)
for i in range(1, n + 1):
if not visited[i]:
print(-1)
return
print(1)
if __name__ == "__main__":
main()
```
### Go
```go
package main
import (
"bufio"
"fmt"
"os"
)
func dfs(graph [][]int, key int, visited []bool) {
visited[key] = true
for _, neighbor := range graph[key] {
if !visited[neighbor] {
dfs(graph, neighbor, visited)
}
}
}
func main() {
scanner := bufio.NewScanner(os.Stdin)
scanner.Scan()
var n, m int
fmt.Sscanf(scanner.Text(), "%d %d", &n, &m)
graph := make([][]int, n+1)
for i := 0; i <= n; i++ {
graph[i] = make([]int, 0)
}
for i := 0; i < m; i++ {
scanner.Scan()
var s, t int
fmt.Sscanf(scanner.Text(), "%d %d", &s, &t)
graph[s] = append(graph[s], t)
}
visited := make([]bool, n+1)
dfs(graph, 1, visited)
for i := 1; i <= n; i++ {
if !visited[i] {
fmt.Println(-1)
return
}
}
fmt.Println(1)
}
```
### Rust
### JavaScript
```javascript
const rl = require('readline').createInterface({
input:process.stdin,
output:process.stdout
})
let inputLines = []
rl.on('line' , (line)=>{
inputLines.push(line)
})
rl.on('close',()=>{
let [n , edgesCount]= inputLines[0].trim().split(' ').map(Number)
let graph = Array.from({length:n+1} , ()=>{return[]})
for(let i = 1 ; i < inputLines.length ; i++ ){
let [from , to] = inputLines[i].trim().split(' ').map(Number)
graph[from].push(to)
}
let visited = new Array(n + 1).fill(false)
let dfs = (graph , key , visited)=>{
if(visited[key]){
return
}
visited[key] = true
for(let nextKey of graph[key]){
dfs(graph,nextKey , visited)
}
}
dfs(graph , 1 , visited)
for(let i = 1 ; i <= n;i++){
if(visited[i] === false){
console.log(-1)
return
}
}
console.log(1)
})
```
### TypeScript
### PhP
### Swift
### Scala
### C#
### Dart
### C