<p align="center">
<a href="https://programmercarl.com/other/xunlianying.html" target="_blank">
  <img src="../pics/训练营.png" width="1000"/>
</a>
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！</strong></p>


> 以为只用了递归，其实还用了回溯

# 257. 二叉树的所有路径

[力扣题目链接](https://leetcode.cn/problems/binary-tree-paths/)

给定一个二叉树，返回所有从根节点到叶子节点的路径。

说明: 叶子节点是指没有子节点的节点。

示例:
![257.二叉树的所有路径1](https://code-thinking-1253855093.file.myqcloud.com/pics/2021020415161576.png)

# 思路

**《代码随想录》算法视频公开课：[递归中带着回溯，你感受到了没？| LeetCode：257. 二叉树的所有路径](https://www.bilibili.com/video/BV1ZG411G7Dh)，相信结合视频在看本篇题解，更有助于大家对本题的理解**。

这道题目要求从根节点到叶子的路径，所以需要前序遍历，这样才方便让父节点指向孩子节点，找到对应的路径。

在这道题目中将第一次涉及到回溯，因为我们要把路径记录下来，需要回溯来回退一个路径再进入另一个路径。

前序遍历以及回溯的过程如图：

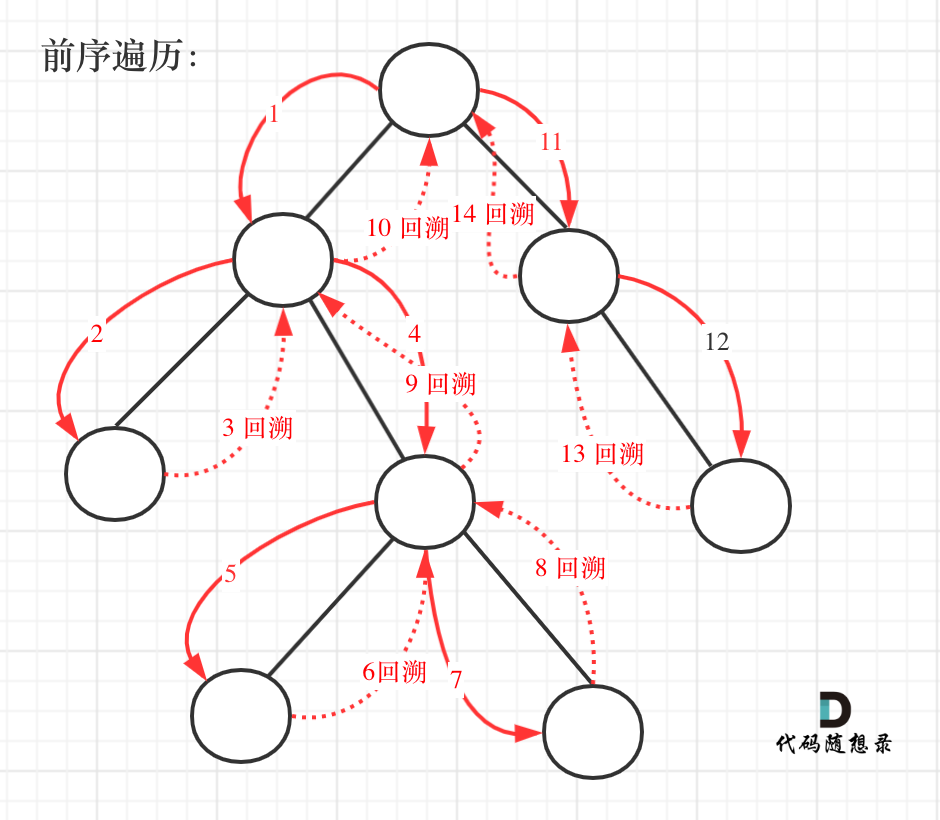
![257.二叉树的所有路径](https://code-thinking-1253855093.file.myqcloud.com/pics/20210204151702443.png)

我们先使用递归的方式，来做前序遍历。**要知道递归和回溯就是一家的，本题也需要回溯。**

## 递归

1. 递归函数参数以及返回值

要传入根节点，记录每一条路径的path，和存放结果集的result，这里递归不需要返回值，代码如下：

```
void traversal(TreeNode* cur, vector<int>& path, vector<string>& result)
```

2. 确定递归终止条件

在写递归的时候都习惯了这么写：

```
if (cur == NULL) {
    终止处理逻辑
}
```

但是本题的终止条件这样写会很麻烦，因为本题要找到叶子节点，就开始结束的处理逻辑了（把路径放进result里）。

**那么什么时候算是找到了叶子节点？** 是当 cur不为空，其左右孩子都为空的时候，就找到叶子节点。

所以本题的终止条件是：
```
if (cur->left == NULL && cur->right == NULL) {
    终止处理逻辑
}
```

为什么没有判断cur是否为空呢，因为下面的逻辑可以控制空节点不入循环。

再来看一下终止处理的逻辑。

这里使用vector<int> 结构path来记录路径，所以要把vector<int> 结构的path转为string格式，再把这个string 放进 result里。

**那么为什么使用了vector<int> 结构来记录路径呢？**  因为在下面处理单层递归逻辑的时候，要做回溯，使用vector方便来做回溯。

可能有的同学问了，我看有些人的代码也没有回溯啊。

**其实是有回溯的，只不过隐藏在函数调用时的参数赋值里**，下文我还会提到。

这里我们先使用vector<int>结构的path容器来记录路径，那么终止处理逻辑如下：

```CPP
if (cur->left == NULL && cur->right == NULL) { // 遇到叶子节点
    string sPath;
    for (int i = 0; i < path.size() - 1; i++) { // 将path里记录的路径转为string格式
        sPath += to_string(path[i]);
        sPath += "->";
    }
    sPath += to_string(path[path.size() - 1]); // 记录最后一个节点（叶子节点）
    result.push_back(sPath); // 收集一个路径
    return;
}
```

3. 确定单层递归逻辑

因为是前序遍历，需要先处理中间节点，中间节点就是我们要记录路径上的节点，先放进path中。

`path.push_back(cur->val);`

然后是递归和回溯的过程，上面说过没有判断cur是否为空，那么在这里递归的时候，如果为空就不进行下一层递归了。

所以递归前要加上判断语句，下面要递归的节点是否为空，如下

```
if (cur->left) {
    traversal(cur->left, path, result);
}
if (cur->right) {
    traversal(cur->right, path, result);
}
```

此时还没完，递归完，要做回溯啊，因为path 不能一直加入节点，它还要删节点，然后才能加入新的节点。

那么回溯要怎么回溯呢，一些同学会这么写，如下：

```CPP
if (cur->left) {
    traversal(cur->left, path, result);
}
if (cur->right) {
    traversal(cur->right, path, result);
}
path.pop_back();
```

这个回溯就有很大的问题，我们知道，**回溯和递归是一一对应的，有一个递归，就要有一个回溯**，这么写的话相当于把递归和回溯拆开了， 一个在花括号里，一个在花括号外。

**所以回溯要和递归永远在一起，世界上最遥远的距离是你在花括号里，而我在花括号外！**

那么代码应该这么写：

```CPP
if (cur->left) {
    traversal(cur->left, path, result);
    path.pop_back(); // 回溯
}
if (cur->right) {
    traversal(cur->right, path, result);
    path.pop_back(); // 回溯
}
```

那么本题整体代码如下：

```CPP
// 版本一
class Solution {
private:

    void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
        path.push_back(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中 
        // 这才到了叶子节点
        if (cur->left == NULL && cur->right == NULL) {
            string sPath;
            for (int i = 0; i < path.size() - 1; i++) {
                sPath += to_string(path[i]);
                sPath += "->";
            }
            sPath += to_string(path[path.size() - 1]);
            result.push_back(sPath);
            return;
        }
        if (cur->left) { // 左 
            traversal(cur->left, path, result);
            path.pop_back(); // 回溯
        }
        if (cur->right) { // 右
            traversal(cur->right, path, result);
            path.pop_back(); // 回溯
        }
    }

public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        vector<int> path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;
    }
};
```
如上的C++代码充分体现了回溯。

那么如上代码可以精简成如下代码：

```CPP
class Solution {
private:

    void traversal(TreeNode* cur, string path, vector<string>& result) {
        path += to_string(cur->val); // 中
        if (cur->left == NULL && cur->right == NULL) {
            result.push_back(path);
            return;
        }
        if (cur->left) traversal(cur->left, path + "->", result); // 左
        if (cur->right) traversal(cur->right, path + "->", result); // 右
    }

public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        string path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;

    }
};
```

如上代码精简了不少，也隐藏了不少东西。

注意在函数定义的时候`void traversal(TreeNode* cur, string path, vector<string>& result)` ，定义的是`string path`，每次都是复制赋值，不用使用引用，否则就无法做到回溯的效果。（这里涉及到C++语法知识）

那么在如上代码中，**貌似没有看到回溯的逻辑，其实不然，回溯就隐藏在`traversal(cur->left, path + "->", result);`中的 `path + "->"`。**  每次函数调用完，path依然是没有加上"->" 的，这就是回溯了。

为了把这份精简代码的回溯过程展现出来，大家可以试一试把：

```CPP
if (cur->left) traversal(cur->left, path + "->", result); // 左  回溯就隐藏在这里
```

改成如下代码：

```CPP
path += "->";
traversal(cur->left, path, result); // 左
```

即：

```CPP
if (cur->left) {
    path += "->";
    traversal(cur->left, path, result); // 左
}
if (cur->right) {
    path += "->";
    traversal(cur->right, path, result); // 右
}
```

此时就没有回溯了，这个代码就是通过不了的了。

如果想把回溯加上，就要 在上面代码的基础上，加上回溯，就可以AC了。

```CPP
if (cur->left) {
    path += "->";
    traversal(cur->left, path, result); // 左
    path.pop_back(); // 回溯 '>'
    path.pop_back(); // 回溯 '-'
}
if (cur->right) {
    path += "->";
    traversal(cur->right, path, result); // 右
    path.pop_back(); // 回溯 '>' 
    path.pop_back(); //  回溯 '-' 
}
```

整体代码如下： 

```CPP 
//版本二
class Solution {
private:
    void traversal(TreeNode* cur, string path, vector<string>& result) {
        path += to_string(cur->val); // 中，中为什么写在这里，因为最后一个节点也要加入到path中
        if (cur->left == NULL && cur->right == NULL) {
            result.push_back(path);
            return;
        }
        if (cur->left) {
            path += "->";
            traversal(cur->left, path, result); // 左
            path.pop_back(); // 回溯 '>'
            path.pop_back(); // 回溯 '-'
        }
        if (cur->right) {
            path += "->";
            traversal(cur->right, path, result); // 右
            path.pop_back(); // 回溯'>'
            path.pop_back(); // 回溯 '-'
        }
    }

public:
    vector<string> binaryTreePaths(TreeNode* root) {
        vector<string> result;
        string path;
        if (root == NULL) return result;
        traversal(root, path, result);
        return result;

    }
};

```

**大家应该可以感受出来，如果把 `path + "->"`作为函数参数就是可以的，因为并没有改变path的数值，执行完递归函数之后，path依然是之前的数值（相当于回溯了）**


**综合以上，第二种递归的代码虽然精简但把很多重要的点隐藏在了代码细节里，第一种递归写法虽然代码多一些，但是把每一个逻辑处理都完整的展现出来了。**

## 拓展 

这里讲解本题解的写法逻辑以及一些更具体的细节，下面的讲解中，涉及到C++语法特性，如果不是C++的录友，就可以不看了，避免越看越晕。 

如果是C++的录友，建议本题独立刷过两遍，再看下面的讲解，同样避免越看越晕，造成不必要的负担。 

在第二版本的代码中，其实仅仅是回溯了 `->` 部分（调用两次pop_back，一个pop`>` 一次pop`-`），大家应该疑惑那么 `path += to_string(cur->val);` 这一步为什么没有回溯呢？ 一条路径能持续加节点 不做回溯吗？  

其实关键还在于 参数，使用的是 `string path`，这里并没有加上引用`&` ，即本层递归中，path + 该节点数值，但该层递归结束，上一层path的数值并不会受到任何影响。  如图所示：

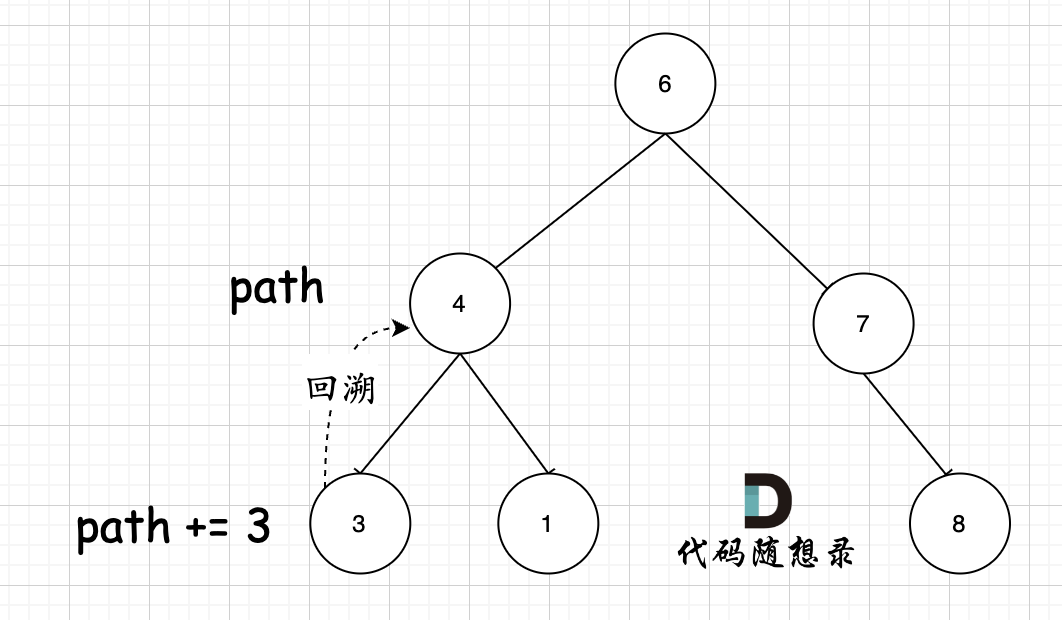
![](https://code-thinking-1253855093.file.myqcloud.com/pics/20220831173322.png) 

节点4 的path，在遍历到节点3，path+3，遍历节点3的递归结束之后，返回节点4（回溯的过程），path并不会把3加上。 

所以这是参数中，不带引用，不做地址拷贝，只做内容拷贝的效果。（这里涉及到C++引用方面的知识） 

在第一个版本中，函数参数我就使用了引用，即 `vector<int>& path` ，这是会拷贝地址的，所以 本层递归逻辑如果有`path.push_back(cur->val);` 就一定要有对应的 `path.pop_back()` 

那有同学可能想，为什么不去定义一个 `string& path` 这样的函数参数呢，然后也可能在递归函数中展现回溯的过程，但关键在于，`path += to_string(cur->val);` 每次是加上一个数字，这个数字如果是个位数，那好说，就调用一次`path.pop_back()`，但如果是 十位数，百位数，千位数呢？ 百位数就要调用三次`path.pop_back()`，才能实现对应的回溯操作，这样代码实现就太冗余了。

所以，第一个代码版本中，我才使用 vector 类型的path，这样方便给大家演示代码中回溯的操作。 vector类型的path，不管 每次 路径收集的数字是几位数，总之一定是int，所以就一次 pop_back就可以。 


## 迭代法


至于非递归的方式，我们可以依然可以使用前序遍历的迭代方式来模拟遍历路径的过程，对该迭代方式不了解的同学，可以看文章[二叉树：听说递归能做的，栈也能做！](https://programmercarl.com/二叉树的迭代遍历.html)和[二叉树：前中后序迭代方式统一写法](https://programmercarl.com/二叉树的统一迭代法.html)。

这里除了模拟递归需要一个栈，同时还需要一个栈来存放对应的遍历路径。

C++代码如下：

```CPP
class Solution {
public:
    vector<string> binaryTreePaths(TreeNode* root) {
        stack<TreeNode*> treeSt;// 保存树的遍历节点
        stack<string> pathSt;   // 保存遍历路径的节点
        vector<string> result;  // 保存最终路径集合
        if (root == NULL) return result;
        treeSt.push(root);
        pathSt.push(to_string(root->val));
        while (!treeSt.empty()) {
            TreeNode* node = treeSt.top(); treeSt.pop(); // 取出节点 中
            string path = pathSt.top();pathSt.pop();    // 取出该节点对应的路径
            if (node->left == NULL && node->right == NULL) { // 遇到叶子节点
                result.push_back(path);
            }
            if (node->right) { // 右
                treeSt.push(node->right);
                pathSt.push(path + "->" + to_string(node->right->val));
            }
            if (node->left) { // 左
                treeSt.push(node->left);
                pathSt.push(path + "->" + to_string(node->left->val));
            }
        }
        return result;
    }
};
```
当然，使用java的同学，可以直接定义一个成员变量为object的栈`Stack<Object> stack = new Stack<>();`，这样就不用定义两个栈了，都放到一个栈里就可以了。

# 总结

**本文我们开始初步涉及到了回溯，很多同学过了这道题目，可能都不知道自己其实使用了回溯，回溯和递归都是相伴相生的。**

我在第一版递归代码中，把递归与回溯的细节都充分的展现了出来，大家可以自己感受一下。

第二版递归代码对于初学者其实非常不友好，代码看上去简单，但是隐藏细节于无形。

最后我依然给出了迭代法。

对于本题充分了解递归与回溯的过程之后，有精力的同学可以再去实现迭代法。


# 其他语言版本

## Java：

```Java
//解法一
class Solution {
    /**
     * 递归法
     */
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> res = new ArrayList<>();// 存最终的结果
        if (root == null) {
            return res;
        }
        List<Integer> paths = new ArrayList<>();// 作为结果中的路径
        traversal(root, paths, res);
        return res;
    }

    private void traversal(TreeNode root, List<Integer> paths, List<String> res) {
        paths.add(root.val);// 前序遍历，中
        // 遇到叶子结点
        if (root.left == null && root.right == null) {
            // 输出
            StringBuilder sb = new StringBuilder();// StringBuilder用来拼接字符串，速度更快
            for (int i = 0; i < paths.size() - 1; i++) {
                sb.append(paths.get(i)).append("->");
            }
            sb.append(paths.get(paths.size() - 1));// 记录最后一个节点
            res.add(sb.toString());// 收集一个路径
            return;
        }
        // 递归和回溯是同时进行，所以要放在同一个花括号里
        if (root.left != null) { // 左
            traversal(root.left, paths, res);
            paths.remove(paths.size() - 1);// 回溯
        }
        if (root.right != null) { // 右
            traversal(root.right, paths, res);
            paths.remove(paths.size() - 1);// 回溯
        }
    }
}
```
```java
// 解法2
class Solution {
    /**
     * 迭代法
     */
    public List<String> binaryTreePaths(TreeNode root) {
        List<String> result = new ArrayList<>();
        if (root == null)
            return result;
        Stack<Object> stack = new Stack<>();
        // 节点和路径同时入栈
        stack.push(root);
        stack.push(root.val + "");
        while (!stack.isEmpty()) {
            // 节点和路径同时出栈
            String path = (String) stack.pop();
            TreeNode node = (TreeNode) stack.pop();
            // 若找到叶子节点
            if (node.left == null && node.right == null) {
                result.add(path);
            }
            //右子节点不为空
            if (node.right != null) {
                stack.push(node.right);
                stack.push(path + "->" + node.right.val);
            }
            //左子节点不为空
            if (node.left != null) {
                stack.push(node.left);
                stack.push(path + "->" + node.left.val);
            }
        }
        return result;
    }
}
```
---
## Python:  
	
	
递归法+回溯（版本一）
```Python
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
import copy
from typing import List, Optional

class Solution:
    def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
        if not root:
            return []
        result = []
        self.generate_paths(root, [], result)
        return result
    
    def generate_paths(self, node: TreeNode, path: List[int], result: List[str]) -> None:
        path.append(node.val)
        if not node.left and not node.right:
            result.append('->'.join(map(str, path)))
        if node.left:
            self.generate_paths(node.left, copy.copy(path), result)
        if node.right:
            self.generate_paths(node.right, copy.copy(path), result)
        path.pop()


```
递归法+回溯（版本二）
```Python
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
import copy
from typing import List, Optional

class Solution:
    def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
        if not root:
            return []
        result = []
        self.generate_paths(root, [], result)
        return result
    
    def generate_paths(self, node: TreeNode, path: List[int], result: List[str]) -> None:
        if not node:
            return
        path.append(node.val)
        if not node.left and not node.right:
            result.append('->'.join(map(str, path)))
        else:
            self.generate_paths(node.left, copy.copy(path), result)
            self.generate_paths(node.right, copy.copy(path), result)
        path.pop()

```
	
递归法+隐形回溯
```Python
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def binaryTreePaths(self, root: TreeNode) -> List[str]:
        path = ''
        result = []
        if not root: return result
        self.traversal(root, path, result)
        return result
    
    def traversal(self, cur: TreeNode, path: str, result: List[str]) -> None:
        path += str(cur.val)
        # 若当前节点为leave，直接输出
        if not cur.left and not cur.right:
            result.append(path)

        if cur.left:
            # + '->' 是隐藏回溯
            self.traversal(cur.left, path + '->', result)
        
        if cur.right:
            self.traversal(cur.right, path + '->', result)
```

迭代法：

```Python
from collections import deque


class Solution:
    """二叉树的所有路径 迭代法"""

    def binaryTreePaths(self, root: TreeNode) -> List[str]:
        # 题目中节点数至少为1
        stack, path_st, result = deque([root]), deque(), []
        path_st.append(str(root.val))

        while stack:
            cur = stack.pop()
            path = path_st.pop()
            # 如果当前节点为叶子节点，添加路径到结果中
            if not (cur.left or cur.right):
                result.append(path)
            if cur.right:
                stack.append(cur.right)
                path_st.append(path + '->' + str(cur.right.val))
            if cur.left:
                stack.append(cur.left)
                path_st.append(path + '->' + str(cur.left.val))

        return result
```

---

## Go：

递归法：

```go
func binaryTreePaths(root *TreeNode) []string {
    res := make([]string, 0)
    var travel func(node *TreeNode, s string)
    travel = func(node *TreeNode, s string) {
        if node.Left == nil && node.Right == nil {
            v := s + strconv.Itoa(node.Val)
            res = append(res, v)
            return
        }
        s = s + strconv.Itoa(node.Val) + "->"
        if node.Left != nil {
            travel(node.Left, s)
        }
        if node.Right != nil {
            travel(node.Right, s)
        }
    }
    travel(root, "")
    return res
}
```

迭代法：

```go
func binaryTreePaths(root *TreeNode) []string {
	stack := []*TreeNode{}
	paths := make([]string, 0)
	res := make([]string, 0)
	if root != nil {
		stack = append(stack, root)
		paths = append(paths, "")
	}
	for len(stack) > 0 {
		l := len(stack)
		node := stack[l-1]
		path := paths[l-1]
		stack = stack[:l-1]
		paths = paths[:l-1]
		if node.Left == nil && node.Right == nil {
			res = append(res, path+strconv.Itoa(node.Val))
			continue
		}
		if node.Right != nil {
			stack = append(stack, node.Right)
			paths = append(paths, path+strconv.Itoa(node.Val)+"->")
		}
		if node.Left != nil {
			stack = append(stack, node.Left)
			paths = append(paths, path+strconv.Itoa(node.Val)+"->")
		}
	}
	return res
}
```

---
## JavaScript:

递归法：

```javascript
var binaryTreePaths = function(root) {
   //递归遍历+递归三部曲
   let res = [];
   //1. 确定递归函数 函数参数
   const getPath = function(node,curPath) {
    //2. 确定终止条件，到叶子节点就终止
       if(node.left === null && node.right === null) {
           curPath += node.val;
           res.push(curPath);
           return;
       }
       //3. 确定单层递归逻辑
       curPath += node.val + '->';
       node.left && getPath(node.left, curPath);
       node.right && getPath(node.right, curPath);
   }
   getPath(root, '');
   return res;
};
```

迭代法：

```javascript
var binaryTreePaths = function(root) {
  if (!root) return [];
  const stack = [root], paths = [''], res = [];
  while (stack.length) {
    const node = stack.pop();
    let path = paths.pop();
    if (!node.left && !node.right) { // 到叶子节点终止, 添加路径到结果中
      res.push(path + node.val);
      continue;
    }
    path += node.val + '->';
    if (node.right) { // 右节点存在
      stack.push(node.right);
      paths.push(path);
    }
    if (node.left) { // 左节点存在
      stack.push(node.left);
      paths.push(path);
    }
  }
  return res;
};  
```

## TypeScript：

> 递归法

```typescript
function binaryTreePaths(root: TreeNode | null): string[] {
    function recur(node: TreeNode, route: string, resArr: string[]): void {
        route += String(node.val);
        if (node.left === null && node.right === null) {
            resArr.push(route);
            return;
        }
        if (node.left !== null) recur(node.left, route + '->', resArr);
        if (node.right !== null) recur(node.right, route + '->', resArr);
    }
    const resArr: string[] = [];
    if (root === null) return resArr;
    recur(root, '', resArr);
    return resArr;
};
```

> 迭代法

```typescript
// 迭代法2
function binaryTreePaths(root: TreeNode | null): string[] {
    let helperStack: TreeNode[] = [];
    let tempNode: TreeNode;
    let routeArr: string[] = [];
    let resArr: string[] = [];
    if (root !== null) {
        helperStack.push(root);
        routeArr.push(String(root.val));
    };
    while (helperStack.length > 0) {
        tempNode = helperStack.pop()!;
        let route: string = routeArr.pop()!; // tempNode 对应的路径
        if (tempNode.left === null && tempNode.right === null) {
            resArr.push(route);
        }
        if (tempNode.right !== null) {
            helperStack.push(tempNode.right);
            routeArr.push(route + '->' + tempNode.right.val);   // tempNode.right 对应的路径
        }
        if (tempNode.left !== null) {
            helperStack.push(tempNode.left);
            routeArr.push(route + '->' + tempNode.left.val);    // tempNode.left 对应的路径
        }
    }
    return resArr;
};
```

## Swift:

> 递归/回溯
```swift
func binaryTreePaths(_ root: TreeNode?) -> [String] {
    var res = [String]()
    guard let root = root else {
        return res
    }
    var path = [Int]()
    _binaryTreePaths(root, path: &path, res: &res)
    return res
}
func _binaryTreePaths(_ root: TreeNode, path: inout [Int], res: inout [String]) {
    path.append(root.val)
    if root.left ==  nil && root.right == nil {
        var str = ""
        for i in 0 ..< path.count - 1 {
            str.append("\(path[i])->")
        }
        str.append("\(path.last!)")
        res.append(str)
        return
    }
    if let left = root.left {
        _binaryTreePaths(left, path: &path, res: &res)
        path.removeLast()
    }
    if let right = root.right {
        _binaryTreePaths(right, path: &path, res: &res)
        path.removeLast()
    }
}
```

> 迭代
```swift
func binaryTreePaths(_ root: TreeNode?) -> [String] {
    var res = [String]()
    guard let root = root else {
        return res
    }
    var stackNode = [TreeNode]()
    stackNode.append(root)
    
    var stackStr = [String]()
    stackStr.append("\(root.val)")
    
    while !stackNode.isEmpty {
        let node = stackNode.popLast()!
        let str = stackStr.popLast()!
        if node.left == nil && node.right == nil {
            res.append(str)
        }
        if let left = node.left {
            stackNode.append(left)
            stackStr.append("\(str)->\(left.val)")
        }
        if let right = node.right {
            stackNode.append(right)
            stackStr.append("\(str)->\(right.val)")
        }
    }
    return res
}
```

## Scala:

递归:
```scala
object Solution {
  import scala.collection.mutable.ListBuffer
  def binaryTreePaths(root: TreeNode): List[String] = {
    val res = ListBuffer[String]()
    def traversal(curNode: TreeNode, path: ListBuffer[Int]): Unit = {
      path.append(curNode.value)
      if (curNode.left == null && curNode.right == null) {
        res.append(path.mkString("->")) // mkString函数: 将数组的所有值按照指定字符串拼接
        return // 处理完可以直接return
      }

      if (curNode.left != null) {
        traversal(curNode.left, path)
        path.remove(path.size - 1)
      }
      if (curNode.right != null) {
        traversal(curNode.right, path)
        path.remove(path.size - 1)
      }
    }
    traversal(root, ListBuffer[Int]())
    res.toList
  }
}
```

rust:

```rust
// 递归
impl Solution {
    pub fn binary_tree_paths(root: Option<Rc<RefCell<TreeNode>>>) -> Vec<String> {
        let mut res = vec![];
        Self::recur(&root, String::from(""), &mut res);
        res
    }
    pub fn recur(node: &Option<Rc<RefCell<TreeNode>>>, mut path: String, res: &mut Vec<String>) {
        let r = node.as_ref().unwrap().borrow();
        path += format!("{}", r.val).as_str();
        if r.left.is_none() && r.right.is_none() {
            res.push(path.to_string());
            return;
        }
        if r.left.is_some() {
            Self::recur(&r.left, path.clone() + "->", res);
        }
        if r.right.is_some() {
            Self::recur(&r.right, path + "->", res);
        }
    }
}
```

<p align="center">
<a href="https://programmercarl.com/other/kstar.html" target="_blank">
  <img src="../pics/网站星球宣传海报.jpg" width="1000"/>
</a>