欢迎大家参与本项目，贡献其他语言版本的代码，拥抱开源，让更多学习算法的小伙伴们收益！

## 538.把二叉搜索树转换为累加树 题目链接：https://leetcode-cn.com/problems/convert-bst-to-greater-tree/ 给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。 提醒一下，二叉搜索树满足下列约束条件： 节点的左子树仅包含键 小于 节点键的节点。 节点的右子树仅包含键 大于 节点键的节点。 左右子树也必须是二叉搜索树。 示例 1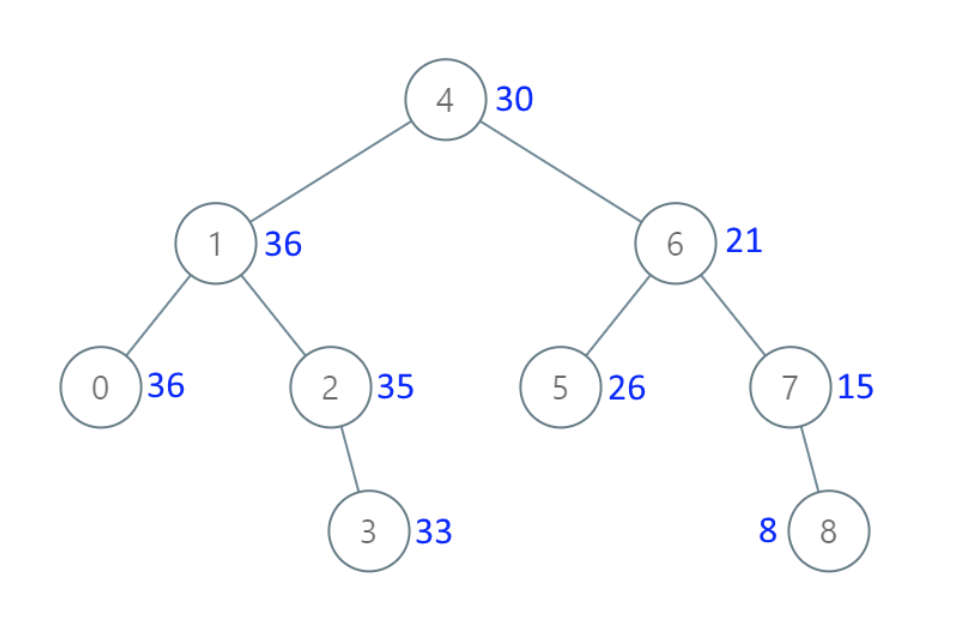： ![538.把二叉搜索树转换为累加树](https://img-blog.csdnimg.cn/20201023160751832.png) 输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8] 输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8] 示例 2： 输入：root = [0,null,1] 输出：[1,null,1] 示例 3： 输入：root = [1,0,2] 输出：[3,3,2] 示例 4： 输入：root = [3,2,4,1] 输出：[7,9,4,10] 提示： * 树中的节点数介于 0 和 104 之间。 * 每个节点的值介于 -104 和 104 之间。 * 树中的所有值 互不相同 。 * 给定的树为二叉搜索树。 ## 思路 一看到累加树，相信很多小伙伴都会疑惑：如何累加？遇到一个节点，然后在遍历其他节点累加？怎么一想这么麻烦呢。 然后再发现这是一颗二叉搜索树，二叉搜索树啊，这是有序的啊。 那么有序的元素如果求累加呢？ **其实这就是一棵树，大家可能看起来有点别扭，换一个角度来看，这就是一个有序数组[2, 5, 13]，求从后到前的累加数组，也就是[20, 18, 13]，是不是感觉这就简单了。** 为什么变成数组就是感觉简单了呢？ 因为数组大家都知道怎么遍历啊，从后向前，挨个累加就完事了，这换成了二叉搜索树，看起来就别扭了一些是不是。 那么知道如何遍历这个二叉树，也就迎刃而解了，**从树中可以看出累加的顺序是右中左，所以我们需要反中序遍历这个二叉树，然后顺序累加就可以了**。 ## 递归 遍历顺序如图所示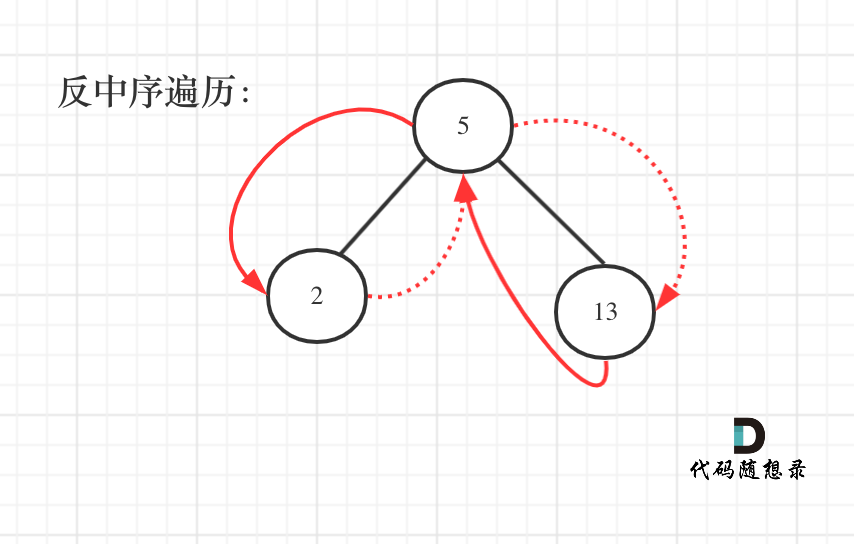： ![538.把二叉搜索树转换为累加树](https://img-blog.csdnimg.cn/20210204153440666.png) 本题依然需要一个pre指针记录当前遍历节点cur的前一个节点，这样才方便做累加。 pre指针的使用技巧，我们在[二叉树：搜索树的最小绝对差](https://mp.weixin.qq.com/s/Hwzml6698uP3qQCC1ctUQQ)和[二叉树：我的众数是多少？](https://mp.weixin.qq.com/s/KSAr6OVQIMC-uZ8MEAnGHg)都提到了，这是常用的操作手段。 * 递归函数参数以及返回值 这里很明确了，不需要递归函数的返回值做什么操作了，要遍历整棵树。 同时需要定义一个全局变量pre，用来保存cur节点的前一个节点的数值，定义为int型就可以了。 代码如下： ``` int pre; // 记录前一个节点的数值 void traversal(TreeNode* cur) ``` * 确定终止条件 遇空就终止。 ``` if (cur == NULL) return; ``` * 确定单层递归的逻辑 注意**要右中左来遍历二叉树**， 中节点的处理逻辑就是让cur的数值加上前一个节点的数值。 代码如下： ``` traversal(cur->right); // 右 cur->val += pre; // 中 pre = cur->val; traversal(cur->left); // 左 ``` 递归法整体代码如下： ```C++ class Solution { private: int pre; // 记录前一个节点的数值 void traversal(TreeNode* cur) { // 右中左遍历 if (cur == NULL) return; traversal(cur->right); cur->val += pre; pre = cur->val; traversal(cur->left); } public: TreeNode* convertBST(TreeNode* root) { pre = 0; traversal(root); return root; } }; ``` ## 迭代法 迭代法其实就是中序模板题了，在[二叉树：前中后序迭代法](https://mp.weixin.qq.com/s/c_zCrGHIVlBjUH_hJtghCg)和[二叉树：前中后序统一方式迭代法](https://mp.weixin.qq.com/s/WKg0Ty1_3SZkztpHubZPRg)可以选一种自己习惯的写法。 这里我给出其中的一种，代码如下： ```C++ class Solution { private: int pre; // 记录前一个节点的数值 void traversal(TreeNode* root) { stack st; TreeNode* cur = root; while (cur != NULL || !st.empty()) { if (cur != NULL) { st.push(cur); cur = cur->right; // 右 } else { cur = st.top(); // 中 st.pop(); cur->val += pre; pre = cur->val; cur = cur->left; // 左 } } } public: TreeNode* convertBST(TreeNode* root) { pre = 0; traversal(root); return root; } }; ``` ## 总结 经历了前面各种二叉树增删改查的洗礼之后，这道题目应该比较简单了。 **好了，二叉树已经接近尾声了，接下来就是要对二叉树来一个大总结了**。 ## 其他语言版本 Java： ```Java class Solution { int sum; public TreeNode convertBST(TreeNode root) { sum = 0; convertBST1(root); return root; } // 按右中左顺序遍历，累加即可 public void convertBST1(TreeNode root) { if (root == null) { return; } convertBST1(root.right); sum += root.val; root.val = sum; convertBST1(root.left); } } ``` Python： ```python3 # Definition for a binary tree node. # class TreeNode: # def __init__(self, val=0, left=None, right=None): # self.val = val # self.left = left # self.right = right #递归法 class Solution: def convertBST(self, root: TreeNode) -> TreeNode: def buildalist(root): if not root: return None buildalist(root.right) #右中左遍历 root.val += self.pre self.pre = root.val buildalist(root.left) self.pre = 0 #记录前一个节点的数值 buildalist(root) return root ``` Go： ----------------------- * 作者微信：[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw) * B站视频：[代码随想录](https://space.bilibili.com/525438321) * 知识星球：[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)