
参与本项目,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们受益!
# 动态规划:完全背包理论基础
本题力扣上没有原题,大家可以去[卡码网第52题](https://kamacoder.com/problempage.php?pid=1052)去练习,题意是一样的。
## 算法公开课
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[带你学透完全背包问题! ](https://www.bilibili.com/video/BV1uK411o7c9/),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
## 思路
### 完全背包
有N件物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。**每件物品都有无限个(也就是可以放入背包多次)**,求解将哪些物品装入背包里物品价值总和最大。
**完全背包和01背包问题唯一不同的地方就是,每种物品有无限件**。
同样leetcode上没有纯完全背包问题,都是需要完全背包的各种应用,需要转化成完全背包问题,所以我这里还是以纯完全背包问题进行讲解理论和原理。
在下面的讲解中,我依然举这个例子:
背包最大重量为4。
物品为:
| | 重量 | 价值 |
| --- | --- | --- |
| 物品0 | 1 | 15 |
| 物品1 | 3 | 20 |
| 物品2 | 4 | 30 |
**每件商品都有无限个!**
问背包能背的物品最大价值是多少?
01背包和完全背包唯一不同就是体现在遍历顺序上,所以本文就不去做动规五部曲了,我们直接针对遍历顺序经行分析!
关于01背包我如下两篇已经进行深入分析了:
* [动态规划:关于01背包问题,你该了解这些!](https://programmercarl.com/背包理论基础01背包-1.html)
* [动态规划:关于01背包问题,你该了解这些!(滚动数组)](https://programmercarl.com/背包理论基础01背包-2.html)
首先再回顾一下01背包的核心代码
```cpp
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
```
我们知道01背包内嵌的循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历,即:
```CPP
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
```
至于为什么,我在[动态规划:关于01背包问题,你该了解这些!(滚动数组)](https://programmercarl.com/背包理论基础01背包-2.html)中也做了讲解。
dp状态图如下:
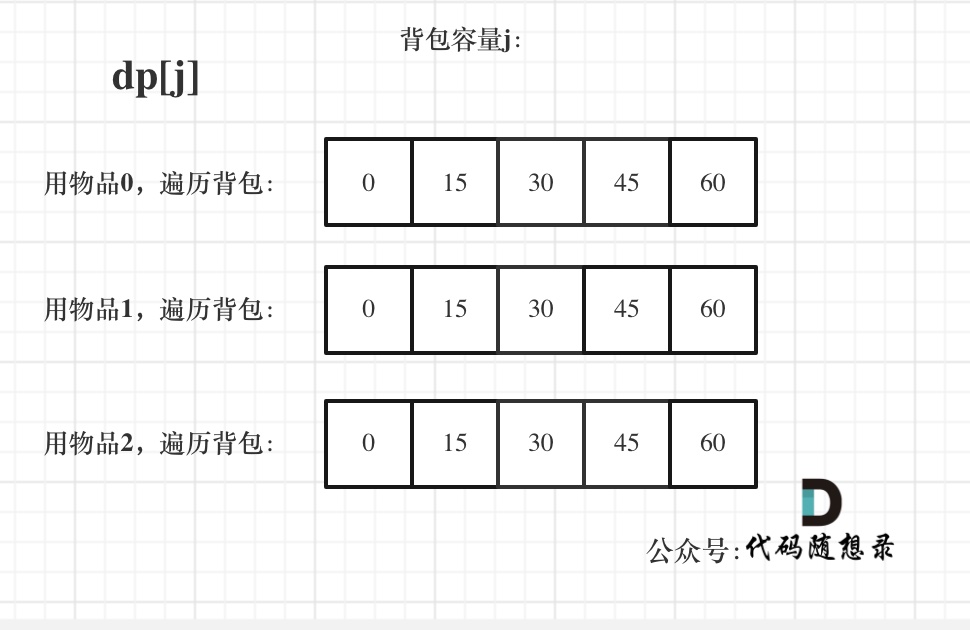
相信很多同学看网上的文章,关于完全背包介绍基本就到为止了。
**其实还有一个很重要的问题,为什么遍历物品在外层循环,遍历背包容量在内层循环?**
这个问题很多题解关于这里都是轻描淡写就略过了,大家都默认 遍历物品在外层,遍历背包容量在内层,好像本应该如此一样,那么为什么呢?
难道就不能遍历背包容量在外层,遍历物品在内层?
看过这两篇的话:
* [动态规划:关于01背包问题,你该了解这些!](https://programmercarl.com/背包理论基础01背包-1.html)
* [动态规划:关于01背包问题,你该了解这些!(滚动数组)](https://programmercarl.com/背包理论基础01背包-2.html)
就知道了,01背包中二维dp数组的两个for遍历的先后循序是可以颠倒了,一维dp数组的两个for循环先后循序一定是先遍历物品,再遍历背包容量。
**在完全背包中,对于一维dp数组来说,其实两个for循环嵌套顺序是无所谓的!**
因为dp[j] 是根据 下标j之前所对应的dp[j]计算出来的。 只要保证下标j之前的dp[j]都是经过计算的就可以了。
遍历物品在外层循环,遍历背包容量在内层循环,状态如图:
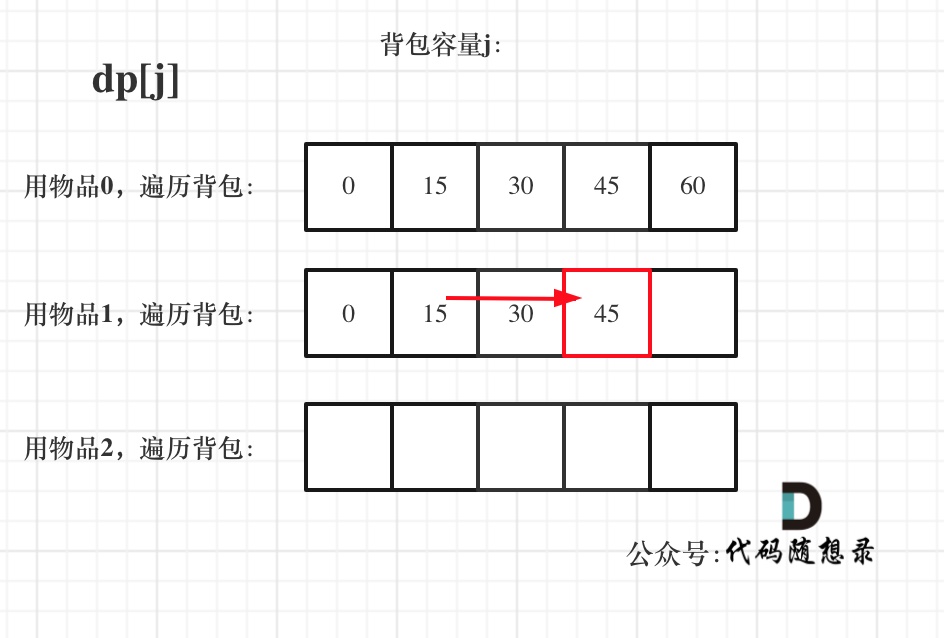
遍历背包容量在外层循环,遍历物品在内层循环,状态如图:
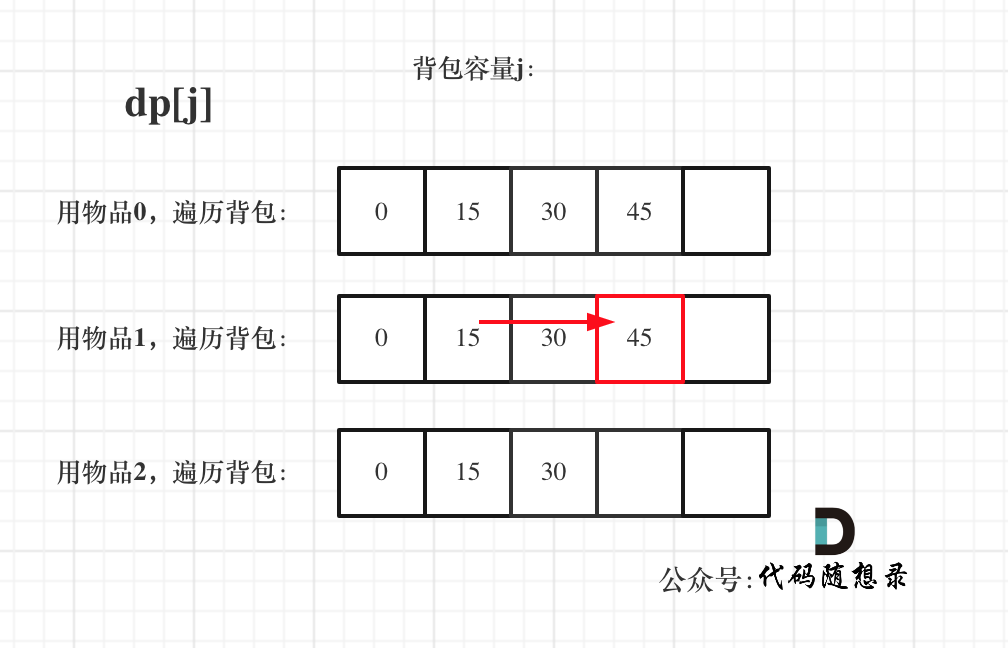
看了这两个图,大家就会理解,完全背包中,两个for循环的先后循序,都不影响计算dp[j]所需要的值(这个值就是下标j之前所对应的dp[j])。
先遍历背包在遍历物品,代码如下:
```CPP
// 先遍历背包,再遍历物品
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 0; i < weight.size(); i++) { // 遍历物品
if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
cout << endl;
}
```
完整的C++测试代码如下:
```CPP
// 先遍历物品,在遍历背包
void test_CompletePack() {
vector weight = {1, 3, 4};
vector value = {15, 20, 30};
int bagWeight = 4;
vector dp(bagWeight + 1, 0);
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = weight[i]; j <= bagWeight; j++) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_CompletePack();
}
```
```CPP
// 先遍历背包,再遍历物品
void test_CompletePack() {
vector weight = {1, 3, 4};
vector value = {15, 20, 30};
int bagWeight = 4;
vector dp(bagWeight + 1, 0);
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 0; i < weight.size(); i++) { // 遍历物品
if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
test_CompletePack();
}
```
本题力扣上没有原题,大家可以去[卡码网第52题](https://kamacoder.com/problempage.php?pid=1052)去练习,题意是一样的,C++代码如下:
```cpp
#include
#include
using namespace std;
// 先遍历背包,再遍历物品
void test_CompletePack(vector weight, vector value, int bagWeight) {
vector dp(bagWeight + 1, 0);
for(int j = 0; j <= bagWeight; j++) { // 遍历背包容量
for(int i = 0; i < weight.size(); i++) { // 遍历物品
if (j - weight[i] >= 0) dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
cout << dp[bagWeight] << endl;
}
int main() {
int N, V;
cin >> N >> V;
vector weight;
vector value;
for (int i = 0; i < N; i++) {
int w;
int v;
cin >> w >> v;
weight.push_back(w);
value.push_back(v);
}
test_CompletePack(weight, value, V);
return 0;
}
```
## 总结
细心的同学可能发现,**全文我说的都是对于纯完全背包问题,其for循环的先后循环是可以颠倒的!**
但如果题目稍稍有点变化,就会体现在遍历顺序上。
如果问装满背包有几种方式的话? 那么两个for循环的先后顺序就有很大区别了,而leetcode上的题目都是这种稍有变化的类型。
这个区别,我将在后面讲解具体leetcode题目中给大家介绍,因为这块如果不结合具题目,单纯的介绍原理估计很多同学会越看越懵!
别急,下一篇就是了!
最后,**又可以出一道面试题了,就是纯完全背包,要求先用二维dp数组实现,然后再用一维dp数组实现,最后再问,两个for循环的先后是否可以颠倒?为什么?**
这个简单的完全背包问题,估计就可以难住不少候选人了。
## 其他语言版本
### Java:
```java
//先遍历物品,再遍历背包
private static void testCompletePack(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 0; i < weight.length; i++){ // 遍历物品
for (int j = weight[i]; j <= bagWeight; j++){ // 遍历背包容量
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}
//先遍历背包,再遍历物品
private static void testCompletePackAnotherWay(){
int[] weight = {1, 3, 4};
int[] value = {15, 20, 30};
int bagWeight = 4;
int[] dp = new int[bagWeight + 1];
for (int i = 1; i <= bagWeight; i++){ // 遍历背包容量
for (int j = 0; j < weight.length; j++){ // 遍历物品
if (i - weight[j] >= 0){
dp[i] = Math.max(dp[i], dp[i - weight[j]] + value[j]);
}
}
}
for (int maxValue : dp){
System.out.println(maxValue + " ");
}
}
```
### Python:
先遍历物品,再遍历背包(无参版)
```python
def test_CompletePack():
weight = [1, 3, 4]
value = [15, 20, 30]
bagWeight = 4
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(weight[i], bagWeight + 1): # 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp[bagWeight])
test_CompletePack()
```
先遍历物品,再遍历背包(有参版)
```python
def test_CompletePack(weight, value, bagWeight):
dp = [0] * (bagWeight + 1)
for i in range(len(weight)): # 遍历物品
for j in range(weight[i], bagWeight + 1): # 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
return dp[bagWeight]
if __name__ == "__main__":
weight = [1, 3, 4]
value = [15, 20, 30]
bagWeight = 4
result = test_CompletePack(weight, value, bagWeight)
print(result)
```
先遍历背包,再遍历物品(无参版)
```python
def test_CompletePack():
weight = [1, 3, 4]
value = [15, 20, 30]
bagWeight = 4
dp = [0] * (bagWeight + 1)
for j in range(bagWeight + 1): # 遍历背包容量
for i in range(len(weight)): # 遍历物品
if j - weight[i] >= 0:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
print(dp[bagWeight])
test_CompletePack()
```
先遍历背包,再遍历物品(有参版)
```python
def test_CompletePack(weight, value, bagWeight):
dp = [0] * (bagWeight + 1)
for j in range(bagWeight + 1): # 遍历背包容量
for i in range(len(weight)): # 遍历物品
if j - weight[i] >= 0:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i])
return dp[bagWeight]
if __name__ == "__main__":
weight = [1, 3, 4]
value = [15, 20, 30]
bagWeight = 4
result = test_CompletePack(weight, value, bagWeight)
print(result)
```
### Go:
```go
// test_CompletePack1 先遍历物品, 在遍历背包
func test_CompletePack1(weight, value []int, bagWeight int) int {
// 定义dp数组 和初始化
dp := make([]int, bagWeight+1)
// 遍历顺序
for i := 0; i < len(weight); i++ {
// 正序会多次添加 value[i]
for j := weight[i]; j <= bagWeight; j++ {
// 推导公式
dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
// debug
//fmt.Println(dp)
}
}
return dp[bagWeight]
}
// test_CompletePack2 先遍历背包, 在遍历物品
func test_CompletePack2(weight, value []int, bagWeight int) int {
// 定义dp数组 和初始化
dp := make([]int, bagWeight+1)
// 遍历顺序
// j从0 开始
for j := 0; j <= bagWeight; j++ {
for i := 0; i < len(weight); i++ {
if j >= weight[i] {
// 推导公式
dp[j] = max(dp[j], dp[j-weight[i]]+value[i])
}
// debug
//fmt.Println(dp)
}
}
return dp[bagWeight]
}
func max(a, b int) int {
if a > b {
return a
}
return b
}
func main() {
weight := []int{1, 3, 4}
price := []int{15, 20, 30}
fmt.Println(test_CompletePack1(weight, price, 4))
fmt.Println(test_CompletePack2(weight, price, 4))
}
```
### Javascript:
```Javascript
// 先遍历物品,再遍历背包容量
function test_completePack1() {
let weight = [1, 3, 5]
let value = [15, 20, 30]
let bagWeight = 4
let dp = new Array(bagWeight + 1).fill(0)
for(let i = 0; i <= weight.length; i++) {
for(let j = weight[i]; j <= bagWeight; j++) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])
}
}
console.log(dp)
}
// 先遍历背包容量,再遍历物品
function test_completePack2() {
let weight = [1, 3, 5]
let value = [15, 20, 30]
let bagWeight = 4
let dp = new Array(bagWeight + 1).fill(0)
for(let j = 0; j <= bagWeight; j++) {
for(let i = 0; i < weight.length; i++) {
if (j >= weight[i]) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i])
}
}
}
console.log(2, dp);
}
```
### TypeScript:
```typescript
// 先遍历物品,再遍历背包容量
function test_CompletePack(): void {
const weight: number[] = [1, 3, 4];
const value: number[] = [15, 20, 30];
const bagSize: number = 4;
const dp: number[] = new Array(bagSize + 1).fill(0);
for (let i = 0; i < weight.length; i++) {
for (let j = weight[i]; j <= bagSize; j++) {
dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);
}
}
console.log(dp);
}
test_CompletePack();
```
### Scala:
```scala
// 先遍历物品,再遍历背包容量
object Solution {
def test_CompletePack() {
var weight = Array[Int](1, 3, 4)
var value = Array[Int](15, 20, 30)
var baseweight = 4
var dp = new Array[Int](baseweight + 1)
for (i <- 0 until weight.length) {
for (j <- weight(i) to baseweight) {
dp(j) = math.max(dp(j), dp(j - weight(i)) + value(i))
}
}
dp(baseweight)
}
}
```
### Rust:
```rust
impl Solution {
// 先遍历物品
fn complete_pack() {
let (goods, bag_size) = (vec![(1, 15), (3, 20), (4, 30)], 4);
let mut dp = vec![0; bag_size + 1];
for (weight, value) in goods {
for j in weight..=bag_size {
dp[j] = dp[j].max(dp[j - weight] + value);
}
}
println!("先遍历物品:{}", dp[bag_size]);
}
// 先遍历背包
fn complete_pack_after() {
let (goods, bag_size) = (vec![(1, 15), (3, 20), (4, 30)], 4);
let mut dp = vec![0; bag_size + 1];
for i in 0..=bag_size {
for (weight, value) in &goods {
if i >= *weight {
dp[i] = dp[i].max(dp[i - weight] + value);
}
}
}
println!("先遍历背包:{}", dp[bag_size]);
}
}
#[test]
fn test_complete_pack() {
Solution::complete_pack();
Solution::complete_pack_after();
}
```

