mirror of
https://github.com/Estom/notes.git
synced 2026-02-03 02:23:31 +08:00
逆序对
This commit is contained in:
@@ -111,4 +111,3 @@ void plus(int pos , int num)
|
||||
}
|
||||
```
|
||||
|
||||
## 实例2 逆序对
|
||||
@@ -1,4 +1,4 @@
|
||||
# 线段树
|
||||
# 线段树Segment Tree
|
||||
|
||||
## 1 线段树的概念
|
||||
|
||||
201
数据结构/6.13 字典树.md
201
数据结构/6.13 字典树.md
@@ -1,201 +0,0 @@
|
||||
# 字典树
|
||||
|
||||
Trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
|
||||
|
||||
字典树设计的核心思想是空间换时间,所以数据结构本身比较消耗空间。但它利用了字符串的**共同前缀(Common Prefix)**作为存储依据,以此来节省存储空间,并加速搜索时间。Trie 的字符串搜索时间复杂度为 **O(m)**,m 为最长的字符串的长度,其查询性能与集合中的字符串的数量无关。其在搜索字符串时表现出的高效,使得特别适用于构建文本搜索和词频统计等应用。
|
||||
|
||||
## Trie 的性质
|
||||
|
||||
- 根节点(Root)不包含字符,除根节点外的每一个节点都仅包含一个字符;
|
||||
- 从根节点到某一节点路径上所经过的字符连接起来,即为该节点对应的字符串;
|
||||
- 任意节点的所有子节点所包含的字符都不相同;
|
||||
|
||||
## Trie 的查找过程
|
||||
|
||||
1. 每次从根结点开始搜索;
|
||||
2. 获取关键词的第一个字符,根据该字符选择对应的子节点,转到该子节点继续检索;
|
||||
3. 在相应的子节点上,获取关键词的第二个字符,进一步选择对应的子节点进行检索;
|
||||
4. 以此类推,进行迭代过程;
|
||||
5. 在某个节点处,关键词的所有字母已被取出,则读取附在该节点上的信息,查找完成。
|
||||
|
||||
## Trie 的应用
|
||||
|
||||
(1)自动补全
|
||||
|
||||

|
||||
|
||||
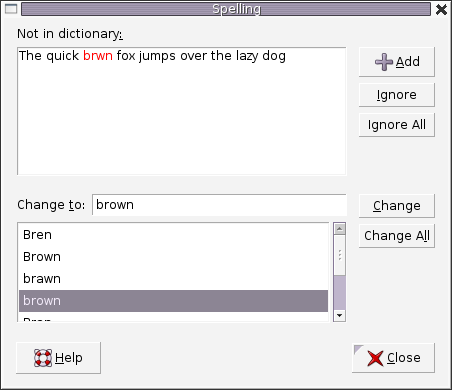
(2)拼写检查
|
||||
|
||||
|
||||
|
||||
(3)IP 路由 (最长前缀匹配)
|
||||
|
||||

|
||||
|
||||
图 3. 使用 Trie 树的最长前缀匹配算法,Internet 协议(IP)路由中利用转发表选择路径。
|
||||
|
||||
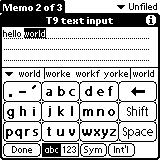
(4)T9 (九宫格) 打字预测
|
||||
|
||||
|
||||
|
||||
(5)单词游戏
|
||||
|
||||

|
||||
|
||||
图 5. Trie 树可通过剪枝搜索空间来高效解决 Boggle 单词游戏
|
||||
|
||||
还有其他的数据结构,如平衡树和哈希表,使我们能够在字符串数据集中搜索单词。为什么我们还需要 Trie 树呢?尽管哈希表可以在 O(1)O(1) 时间内寻找键值,却无法高效的完成以下操作:
|
||||
|
||||
- 找到具有同一前缀的全部键值。
|
||||
- 按词典序枚举字符串的数据集。
|
||||
|
||||
Trie 树优于哈希表的另一个理由是,随着哈希表大小增加,会出现大量的冲突,时间复杂度可能增加到 $$O(n)$$,其中 n 是插入的键的数量。与哈希表相比,Trie 树在存储多个具有相同前缀的键时可以使用较少的空间。此时 Trie 树只需要 $$O(m)$$ 的时间复杂度,其中 m 为键长。而在平衡树中查找键值需要 $$O(mlogn)$$ 时间复杂度。
|
||||
|
||||
## Trie 树的结点结构
|
||||
|
||||
Trie 树是一个有根的树,其结点具有以下字段:。
|
||||
|
||||
最多 R 个指向子结点的链接,其中每个链接对应字母表数据集中的一个字母。
|
||||
|
||||
- 本文中假定 R 为 26,小写拉丁字母的数量。
|
||||
- 布尔字段,以指定节点是对应键的结尾还是只是键前缀。
|
||||
|
||||

|
||||
|
||||
```java
|
||||
class TrieNode {
|
||||
|
||||
// R links to node children
|
||||
private TrieNode[] links;
|
||||
|
||||
private final int R = 26;
|
||||
|
||||
private boolean isEnd;
|
||||
|
||||
public TrieNode() {
|
||||
links = new TrieNode[R];
|
||||
}
|
||||
|
||||
public boolean containsKey(char ch) {
|
||||
return links[ch -'a'] != null;
|
||||
}
|
||||
public TrieNode get(char ch) {
|
||||
return links[ch -'a'];
|
||||
}
|
||||
public void put(char ch, TrieNode node) {
|
||||
links[ch -'a'] = node;
|
||||
}
|
||||
public void setEnd() {
|
||||
isEnd = true;
|
||||
}
|
||||
public boolean isEnd() {
|
||||
return isEnd;
|
||||
}
|
||||
}
|
||||
```
|
||||
向 Trie 树中插入键
|
||||
|
||||
我们通过搜索 Trie 树来插入一个键。我们从根开始搜索它对应于第一个键字符的链接。有两种情况:
|
||||
|
||||
- 链接存在。沿着链接移动到树的下一个子层。算法继续搜索下一个键字符。
|
||||
- 链接不存在。创建一个新的节点,并将它与父节点的链接相连,该链接与当前的键字符相匹配。
|
||||
|
||||
重复以上步骤,直到到达键的最后一个字符,然后将当前节点标记为结束节点,算法完成。
|
||||
|
||||
图 7. 向 Trie 树中插入键
|
||||
|
||||
Java
|
||||
class Trie {
|
||||
private TrieNode root;
|
||||
|
||||
public Trie() {
|
||||
root = new TrieNode();
|
||||
}
|
||||
|
||||
// Inserts a word into the trie.
|
||||
public void insert(String word) {
|
||||
TrieNode node = root;
|
||||
for (int i = 0; i < word.length(); i++) {
|
||||
char currentChar = word.charAt(i);
|
||||
if (!node.containsKey(currentChar)) {
|
||||
node.put(currentChar, new TrieNode());
|
||||
}
|
||||
node = node.get(currentChar);
|
||||
}
|
||||
node.setEnd();
|
||||
}
|
||||
}
|
||||
复杂度分析
|
||||
|
||||
时间复杂度:O(m)O(m),其中 mm 为键长。在算法的每次迭代中,我们要么检查要么创建一个节点,直到到达键尾。只需要 mm 次操作。
|
||||
|
||||
空间复杂度:O(m)O(m)。最坏的情况下,新插入的键和 Trie 树中已有的键没有公共前缀。此时需要添加 mm 个结点,使用 O(m)O(m) 空间。
|
||||
|
||||
在 Trie 树中查找键
|
||||
每个键在 trie 中表示为从根到内部节点或叶的路径。我们用第一个键字符从根开始,。检查当前节点中与键字符对应的链接。有两种情况:
|
||||
|
||||
存在链接。我们移动到该链接后面路径中的下一个节点,并继续搜索下一个键字符。
|
||||
不存在链接。若已无键字符,且当前结点标记为 isEnd,则返回 true。否则有两种可能,均返回 false :
|
||||
还有键字符剩余,但无法跟随 Trie 树的键路径,找不到键。
|
||||
没有键字符剩余,但当前结点没有标记为 isEnd。也就是说,待查找键只是Trie树中另一个键的前缀。
|
||||
|
||||
|
||||
图 8. 在 Trie 树中查找键
|
||||
|
||||
Java
|
||||
class Trie {
|
||||
...
|
||||
|
||||
// search a prefix or whole key in trie and
|
||||
// returns the node where search ends
|
||||
private TrieNode searchPrefix(String word) {
|
||||
TrieNode node = root;
|
||||
for (int i = 0; i < word.length(); i++) {
|
||||
char curLetter = word.charAt(i);
|
||||
if (node.containsKey(curLetter)) {
|
||||
node = node.get(curLetter);
|
||||
} else {
|
||||
return null;
|
||||
}
|
||||
}
|
||||
return node;
|
||||
}
|
||||
|
||||
// Returns if the word is in the trie.
|
||||
public boolean search(String word) {
|
||||
TrieNode node = searchPrefix(word);
|
||||
return node != null && node.isEnd();
|
||||
}
|
||||
}
|
||||
复杂度分析
|
||||
|
||||
时间复杂度 : O(m)O(m)。算法的每一步均搜索下一个键字符。最坏的情况下需要 mm 次操作。
|
||||
空间复杂度 : O(1)O(1)。
|
||||
查找 Trie 树中的键前缀
|
||||
该方法与在 Trie 树中搜索键时使用的方法非常相似。我们从根遍历 Trie 树,直到键前缀中没有字符,或者无法用当前的键字符继续 Trie 中的路径。与上面提到的“搜索键”算法唯一的区别是,到达键前缀的末尾时,总是返回 true。我们不需要考虑当前 Trie 节点是否用 “isend” 标记,因为我们搜索的是键的前缀,而不是整个键。
|
||||
|
||||
|
||||
|
||||
图 9. 查找 Trie 树中的键前缀
|
||||
|
||||
Java
|
||||
class Trie {
|
||||
...
|
||||
|
||||
// Returns if there is any word in the trie
|
||||
// that starts with the given prefix.
|
||||
public boolean startsWith(String prefix) {
|
||||
TrieNode node = searchPrefix(prefix);
|
||||
return node != null;
|
||||
}
|
||||
}
|
||||
复杂度分析
|
||||
|
||||
时间复杂度 : O(m)O(m)。
|
||||
空间复杂度 : O(1)O(1)。
|
||||
|
||||
## 实战
|
||||
|
||||
## 参考资料
|
||||
|
||||
- https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/shi-xian-trie-qian-zhui-shu-by-leetcode/D:\Codes\ZPTutorial\ZPSpring\spring-boot-tutorial\codes\spring-boot-dubbo\README.md
|
||||
191
数据结构/6.9 字典树.md
Normal file
191
数据结构/6.9 字典树.md
Normal file
@@ -0,0 +1,191 @@
|
||||
# 字典树Trie
|
||||
|
||||
> 参考资料
|
||||
> - [字典树trie](https://leetcode-cn.com/problems/implement-trie-prefix-tree/solution/shi-xian-trie-qian-zhui-shu-by-leetcode/D:\Codes\ZPTutorial\ZPSpring\spring-boot-tutorial\codes\spring-boot-dubbo\README.md)
|
||||
> - [数据结构算法10](https://blog.csdn.net/yuzhiqiang666/article/details/80711441)
|
||||
|
||||
|
||||
## 1 Trie定义
|
||||
* Trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
|
||||
|
||||
* 字典树设计的核心思想是空间换时间,所以数据结构本身比较消耗空间。但它利用了字符串的**共同前缀(Common Prefix)**作为存储依据,以此来节省存储空间,并加速搜索时间。Trie 的字符串搜索时间复杂度为 **O(m)**,m为最长的字符串的长度,其查询性能与集合中的字符串的数量无关。其在搜索字符串时表现出的高效,使得特别适用于构建文本搜索和词频统计等应用。
|
||||
|
||||
## 2 Trie 的性质
|
||||
|
||||
- 根节点(Root)不包含字符,除根节点外的每一个节点都仅包含一个字符;
|
||||
- 从根节点到某一节点路径上所经过的字符连接起来,即为该节点对应的字符串;
|
||||
- 任意节点的所有子节点所包含的字符都不相同;
|
||||
|
||||
## 3 Trie 的查找过程
|
||||
|
||||
1. 每次从根结点开始搜索;
|
||||
2. 获取关键词的第一个字符,根据该字符选择对应的子节点,转到该子节点继续检索;
|
||||
3. 在相应的子节点上,获取关键词的第二个字符,进一步选择对应的子节点进行检索;
|
||||
4. 以此类推,进行迭代过程;
|
||||
5. 在某个节点处,关键词的所有字母已被取出,则读取附在该节点上的信息,查找完成。
|
||||
|
||||
## 4 Trie 的应用
|
||||
|
||||
### 自动补全
|
||||
|
||||

|
||||
|
||||
### 拼写检查
|
||||
|
||||

|
||||
|
||||
### IP 路由 (最长前缀匹配)
|
||||
|
||||

|
||||
|
||||
> 使用 Trie 树的最长前缀匹配算法,Internet 协议(IP)路由中利用转发表选择路径。
|
||||
|
||||
### T9 (九宫格) 打字预测
|
||||
|
||||

|
||||
|
||||
### 单词游戏
|
||||
|
||||

|
||||
|
||||
> Trie 树可通过剪枝搜索空间来高效解决 Boggle 单词游戏
|
||||
|
||||
* 还有其他的数据结构,如平衡树和哈希表,使我们能够在字符串数据集中搜索单词。为什么我们还需要 Trie 树呢?尽管哈希表可以在 O(1)O(1) 时间内寻找键值,却无法高效的完成以下操作:
|
||||
- 找到具有同一前缀的全部键值。
|
||||
- 按词典序枚举字符串的数据集。
|
||||
|
||||
* Trie 树优于哈希表的另一个理由是,随着哈希表大小增加,会出现大量的冲突,时间复杂度可能增加到 $$O(n)$$,其中 n 是插入的键的数量。与哈希表相比,Trie 树在存储多个具有相同前缀的键时可以使用较少的空间。此时 Trie 树只需要 $$O(m)$$ 的时间复杂度,其中 m 为键长。而在平衡树中查找键值需要 $$O(mlogn)$$ 时间复杂度。
|
||||
|
||||
## 5 Trie 树的结点结构
|
||||
|
||||
* Trie 树是一个有根的树,其结点具有以下字段:最多 R 个指向子结点的链接,其中每个链接对应字母表数据集中的一个字母。
|
||||
|
||||
- 本文中假定 R 为 26,小写拉丁字母的数量。
|
||||
- 布尔字段,以指定节点是对应键的结尾还是只是键前缀。
|
||||
|
||||
```java
|
||||
class TrieNode {
|
||||
|
||||
// R links to node children
|
||||
private TrieNode[] links;
|
||||
|
||||
private final int R = 26;
|
||||
|
||||
private boolean isEnd;
|
||||
|
||||
public TrieNode() {
|
||||
links = new TrieNode[R];
|
||||
}
|
||||
|
||||
public boolean containsKey(char ch) {
|
||||
return links[ch -'a'] != null;
|
||||
}
|
||||
public TrieNode get(char ch) {
|
||||
return links[ch -'a'];
|
||||
}
|
||||
public void put(char ch, TrieNode node) {
|
||||
links[ch -'a'] = node;
|
||||
}
|
||||
public void setEnd() {
|
||||
isEnd = true;
|
||||
}
|
||||
public boolean isEnd() {
|
||||
return isEnd;
|
||||
}
|
||||
}
|
||||
```
|
||||
|
||||
## 6 Tire树的插入
|
||||
* 向 Trie 树中插入键。我们通过搜索 Trie 树来插入一个键。我们从根开始搜索它对应于第一个键字符的链接。有两种情况:
|
||||
- 链接存在。沿着链接移动到树的下一个子层。算法继续搜索下一个键字符。
|
||||
- 链接不存在。创建一个新的节点,并将它与父节点的链接相连,该链接与当前的键字符相匹配。
|
||||
|
||||
* 重复以上步骤,直到到达键的最后一个字符,然后将当前节点标记为结束节点,算法完成。
|
||||
|
||||
```Java
|
||||
class Trie {
|
||||
private TrieNode root;
|
||||
|
||||
public Trie() {
|
||||
root = new TrieNode();
|
||||
}
|
||||
|
||||
// Inserts a word into the trie.
|
||||
public void insert(String word) {
|
||||
TrieNode node = root;
|
||||
for (int i = 0; i < word.length(); i++) {
|
||||
char currentChar = word.charAt(i);
|
||||
if (!node.containsKey(currentChar)) {
|
||||
node.put(currentChar, new TrieNode());
|
||||
}
|
||||
node = node.get(currentChar);
|
||||
}
|
||||
node.setEnd();
|
||||
}
|
||||
}
|
||||
```
|
||||
### 复杂度分析
|
||||
|
||||
* 时间复杂度:O(m),其中 m 为键长。在算法的每次迭代中,我们要么检查要么创建一个节点,直到到达键尾。只需要 m 次操作。
|
||||
|
||||
* 空间复杂度:O(m)。最坏的情况下,新插入的键和 Trie 树中已有的键没有公共前缀。此时需要添加 m 个结点,使用O(m) 空间。
|
||||
|
||||
## 7 Trie树查找键
|
||||
|
||||
* 每个键在 trie 中表示为从根到内部节点或叶的路径。我们用第一个键字符从根开始,。检查当前节点中与键字符对应的链接。有两种情况:
|
||||
* 存在链接。我们移动到该链接后面路径中的下一个节点,并继续搜索下一个键字符。
|
||||
* 不存在链接。若已无键字符,且当前结点标记为 isEnd,则返回 true。否则有两种可能,均返回 false :
|
||||
* 还有键字符剩余,但无法跟随 Trie 树的键路径,找不到键。
|
||||
* 没有键字符剩余,但当前结点没有标记为 isEnd。也就是说,待查找键只是Trie树中另一个键的前缀。
|
||||
|
||||
|
||||
```Java
|
||||
class Trie {
|
||||
...
|
||||
|
||||
// search a prefix or whole key in trie and
|
||||
// returns the node where search ends
|
||||
private TrieNode searchPrefix(String word) {
|
||||
TrieNode node = root;
|
||||
for (int i = 0; i < word.length(); i++) {
|
||||
char curLetter = word.charAt(i);
|
||||
if (node.containsKey(curLetter)) {
|
||||
node = node.get(curLetter);
|
||||
} else {
|
||||
return null;
|
||||
}
|
||||
}
|
||||
return node;
|
||||
}
|
||||
|
||||
// Returns if the word is in the trie.
|
||||
public boolean search(String word) {
|
||||
TrieNode node = searchPrefix(word);
|
||||
return node != null && node.isEnd();
|
||||
}
|
||||
}
|
||||
```
|
||||
### 复杂度分析
|
||||
|
||||
* 时间复杂度 : O(m)O(m)。算法的每一步均搜索下一个键字符。最坏的情况下需要 mm 次操作。
|
||||
* 空间复杂度 : O(1)O(1)。
|
||||
|
||||
## 8 Trie树查找键前缀
|
||||
* 该方法与在 Trie 树中搜索键时使用的方法非常相似。我们从根遍历 Trie 树,直到键前缀中没有字符,或者无法用当前的键字符继续 Trie 中的路径。与上面提到的“搜索键”算法唯一的区别是,到达键前缀的末尾时,总是返回 true。我们不需要考虑当前 Trie 节点是否用 “isend” 标记,因为我们搜索的是键的前缀,而不是整个键。
|
||||
|
||||
```Java
|
||||
class Trie {
|
||||
...
|
||||
|
||||
// Returns if there is any word in the trie
|
||||
// that starts with the given prefix.
|
||||
public boolean startsWith(String prefix) {
|
||||
TrieNode node = searchPrefix(prefix);
|
||||
return node != null;
|
||||
}
|
||||
}
|
||||
```
|
||||
### 复杂度分析
|
||||
|
||||
* 时间复杂度 : O(m)。
|
||||
* 空间复杂度 : O(1)。
|
||||
@@ -11,7 +11,7 @@
|
||||
### 策略选择
|
||||
|
||||
* 数据结构:线性数组
|
||||
* 算法思想:变质法。将搜索查找问题修改为排序问题。归并排序
|
||||
* 算法思想:变治法。将搜索查找问题修改为排序问题。归并排序
|
||||
|
||||
### 算法设计
|
||||
|
||||
|
||||
@@ -3,4 +3,13 @@
|
||||
* 一个问题。强相关的标签有三个。属于哪一类问题。使用哪些算法思想。问题属于哪一种数据结构。因为vscode的文件组织方式为树形结构。只能支持单一索引,无法支持多种类别的标签索引。
|
||||
* 所以最终决定。应该将不断增长的爆炸性问题。转移到C类:问题算法中。主要用来记录在解决问题中的思考和见解。根据问题类型对算法分类。记录算法。
|
||||
|
||||
## 分类说明
|
||||
|
||||
* 与数据结构强相关的算法
|
||||
* 与算法思想强相关的算法
|
||||
* 与问题目标强相关的算法
|
||||
|
||||
|
||||
## 命名说明
|
||||
|
||||
* 以某一类算法的名称明明,而不是某一个算法明明。收集找到该类别下的相关算法。
|
||||
|
||||
@@ -5,7 +5,7 @@
|
||||
* 输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
|
||||
* [链接](https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof/)
|
||||
|
||||
## 1 二叉树与双向链表——左旋右旋
|
||||
## 1.1 二叉树与双向链表——左旋右旋
|
||||
|
||||
> 借鉴了构建二叉平衡树的内容。可以自己完成以下二叉平衡树试试。
|
||||
|
||||
@@ -138,3 +138,6 @@ private:
|
||||
}
|
||||
```
|
||||
|
||||
## 2 堆树的上浮下沉操作
|
||||
|
||||
## 3 二叉平衡树的左旋右旋
|
||||
0
算法/B类:数据结构算法/3.1 单调栈.md
Normal file
0
算法/B类:数据结构算法/3.1 单调栈.md
Normal file
97
算法/B类:数据结构算法/4.4 线性区间操作.md
Normal file
97
算法/B类:数据结构算法/4.4 线性区间操作.md
Normal file
@@ -0,0 +1,97 @@
|
||||
# 线性区间操作
|
||||
|
||||
## 区间操作分类
|
||||
|
||||
* 修改区间值,询问元素值。(差分数组)
|
||||
* 修改元素值,访问区间值。(树状数组和线段树)
|
||||
* 修改元素值,查询最大最小值。(线段树)
|
||||
|
||||
## 1 数组中的逆序对
|
||||
|
||||
|
||||
### 问题描述
|
||||
|
||||
在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
|
||||
|
||||
### 问题分析
|
||||
|
||||
|
||||
|
||||
### 策略选择
|
||||
|
||||
* 数据结构:线性数组、树状数组
|
||||
* 算法思想:用树状数组解决逆序数问题,也是一个经典的做法。树状数组是一种实现了高效查询「前缀和」与「单点更新」操作的数据结构,
|
||||
|
||||
|
||||
### 算法设计
|
||||
|
||||
具体的做法是:
|
||||
* 先离散化,将所有的数组元素映射到 0、1、2、3... ,这是为了节约树状数组的空间;
|
||||
* 从后向前扫描,边统计边往树状数组里面添加元素,这个过程是「动态的」,需要动手计算才能明白思想。
|
||||
|
||||
|
||||
|
||||
* 我们可以看出它第i−1 位的前缀和表示「有多少个数比 i 小」。那么我们可以从后往前遍历序列a,记当前遍历到的元素为 $a_i$,我们把$a_i$对应的桶的值自增 1,把 i - 1位置的前缀和加入到答案中算贡献。
|
||||
|
||||
* 我们显然可以用数组来实现这个桶,可问题是如果$a_i$中有很大的元素,比如 10^9我们就要开一个大小为 10^9的桶,内存中是存不下的。这个桶数组中很多位置是0,有效位置是稀疏的,我们要想一个办法让有效的位置全聚集到一起,减少无效位置的出现,这个时候我们就需要用到一个方法——离散化。
|
||||
|
||||
* 离散化一个序列的前提是我们只关心这个序列里面元素的相对大小,而不关心绝对大小(即只关心元素在序列中的排名);离散化的目的是让原来分布零散的值聚集到一起,减少空间浪费。那么如何获得元素排名呢,我们可以对原序列排序后去重,对于每一个$a_i$通过二分查找的方式计算排名作为离散化之后的值。当然这里也可以不去重,不影响排名。
|
||||
|
||||
### 算法分析
|
||||
|
||||
* 时间复杂度为 O(n \log n)
|
||||
* 空间复杂度为 O(n)O(n)
|
||||
|
||||
|
||||
### 算法实现
|
||||
```
|
||||
class BIT {
|
||||
private:
|
||||
vector<int> tree;
|
||||
int n;
|
||||
|
||||
public:
|
||||
BIT(int _n): n(_n), tree(_n + 1) {}
|
||||
|
||||
static int lowbit(int x) {
|
||||
return x & (-x);
|
||||
}
|
||||
|
||||
int query(int x) {
|
||||
int ret = 0;
|
||||
while (x) {
|
||||
ret += tree[x];
|
||||
x -= lowbit(x);
|
||||
}
|
||||
return ret;
|
||||
}
|
||||
|
||||
void update(int x) {
|
||||
while (x <= n) {
|
||||
++tree[x];
|
||||
x += lowbit(x);
|
||||
}
|
||||
}
|
||||
};
|
||||
|
||||
class Solution {
|
||||
public:
|
||||
int reversePairs(vector<int>& nums) {
|
||||
int n = nums.size();
|
||||
vector<int> tmp = nums;
|
||||
// 离散化
|
||||
sort(tmp.begin(), tmp.end());
|
||||
for (int& num: nums) {
|
||||
num = lower_bound(tmp.begin(), tmp.end(), num) - tmp.begin() + 1;
|
||||
}
|
||||
// 树状数组统计逆序对
|
||||
BIT bit(n);
|
||||
int ans = 0;
|
||||
for (int i = n - 1; i >= 0; --i) {
|
||||
ans += bit.query(nums[i] - 1);
|
||||
bit.update(nums[i]);
|
||||
}
|
||||
return ans;
|
||||
}
|
||||
};
|
||||
```
|
||||
Reference in New Issue
Block a user