CS_ALearn/ailearning
1
0
Fork 0
mirror of https://github.com/apachecn/ailearning.git synced 2026-02-03 02:14:18 +08:00
Code Issues Projects Releases Wiki Activity

2020-10-19 20:56:03

Browse Source
This commit is contained in:
wizardforcel
2020-10-19 20:56:03 +08:00
parent a91b352944
commit 24c6d8d141
19 changed files with 6676 additions and 6676 deletions
Download Patch File Download Diff File Expand all files Collapse all files

34
SUMMARY.md
View File

@@ -1,24 +1,24 @@
+ [入门须知](README.md)
+ 机器学习
+ [第1章_基础知识](docs/ml/1.机器学习基础.md)
+ [第2章_K近邻算法](docs/ml/2.k-近邻算法.md)
+ [第3章_决策树算法](docs/ml/3.决策树.md)
+ [第4章_朴素贝叶斯](docs/ml/4.朴素贝叶斯.md)
+ [第5章_逻辑回归](docs/ml/5.Logistic回归.md)
+ [第6章_支持向量机](docs/ml/6.支持向量机.md)
+ [第7章_集成方法](docs/ml/7.集成方法-随机森林和AdaBoost.md)
+ [第8章_回归](docs/ml/8.回归.md)
+ [第9章_树回归](docs/ml/9.树回归.md)
+ [第10章_KMeans聚类](docs/ml/10.KMeans聚类.md)
+ [第11章_Apriori算法](docs/ml/11.使用Apriori算法进行关联分析.md)
+ [第12章_FP-growth算法](docs/ml/12.使用FP-growth算法来高效发现频繁项集.md)
+ [第13章_PCA降维](docs/ml/13.利用PCA来简化数据.md)
+ [第14章_SVD简化数据](docs/ml/14.利用SVD简化数据.md)
+ [第15章_大数据与MapReduce](docs/ml/15.大数据与MapReduce.md)
+ [第16章_推荐系统](docs/ml/16.推荐系统.md)
+ [第1章_基础知识](docs/ml/1.md)
+ [第2章_K近邻算法](docs/ml/2.md)
+ [第3章_决策树算法](docs/ml/3.md)
+ [第4章_朴素贝叶斯](docs/ml/4.md)
+ [第5章_逻辑回归](docs/ml/5.md)
+ [第6章_支持向量机](docs/ml/6.md)
+ [第7章_集成方法](docs/ml/7.md)
+ [第8章_回归](docs/ml/8.md)
+ [第9章_树回归](docs/ml/9.md)
+ [第10章_KMeans聚类](docs/ml/10.md)
+ [第11章_Apriori算法](docs/ml/11.md)
+ [第12章_FP-growth算法](docs/ml/12.md)
+ [第13章_PCA降维](docs/ml/13.md)
+ [第14章_SVD简化数据](docs/ml/14.md)
+ [第15章_大数据与MapReduce](docs/ml/15.md)
+ [第16章_推荐系统](docs/ml/16.md)
+ [为何录制教学版视频](docs/why-to-record-study-ml-video.md)
+ [2017-04-08_第一期的总结](report/2017-04-08_第一期的总结.md)
+ [2017-04-08_第一期的总结](docs/report/2017-04-08.md)
+ 深度学习入门
+ [反向传递](docs/dl/反向传递.md)
+ [CNN原理](docs/dl/CNN原理.md)

478
docs/ml/1.机器学习基础.md → docs/ml/1.md
View File

@@ -1,239 +1,239 @@
# 第1章 机器学习基础
![机器学习基础_首页](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/机器学习基础-首页.jpg)
## 机器学习 概述
`机器学习(Machine Learning,ML)` 是使用计算机来彰显数据背后的真实含义，它为了把无序的数据转换成有用的信息。是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。
它是人工智能的核心，是使计算机具有智能的根本途径，其应用遍及人工智能的各个领域，它主要使用归纳、综合而不是演绎。
1. 海量的数据
2. 获取有用的信息
## 机器学习 研究意义
机器学习是一门人工智能的科学，该领域的主要研究对象是人工智能，特别是如何在经验学习中改善具体算法的性能”。 “机器学习是对能通过经验自动改进的计算机算法的研究”。 “机器学习是用数据或以往的经验，以此优化计算机程序的性能标准。” 一种经常引用的英文定义是: A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
机器学习已经有了十分广泛的应用，例如: 数据挖掘、计算机视觉、自然语言处理、生物特征识别、搜索引擎、医学诊断、检测信用卡欺诈、证券市场分析、DNA序列测序、语音和手写识别、战略游戏和机器人运用。
## 机器学习 场景
* 例如: 识别动物猫
* 模式识别（官方标准）: 人们通过大量的经验，得到结论，从而判断它就是猫。
* 机器学习（数据学习）: 人们通过阅读进行学习，观察它会叫、小眼睛、两只耳朵、四条腿、一条尾巴，得到结论，从而判断它就是猫。
* 深度学习（深入数据）: 人们通过深入了解它，发现它会'喵喵'的叫、与同类的猫科动物很类似，得到结论，从而判断它就是猫。（深度学习常用领域: 语音识别、图像识别）
* 模式识别（pattern recognition）: 模式识别是最古老的（作为一个术语而言，可以说是很过时的）。
* 我们把环境与客体统称为“模式”，识别是对模式的一种认知，是如何让一个计算机程序去做一些看起来很“智能”的事情。
* 通过融于智慧和直觉后，通过构建程序，识别一些事物，而不是人，例如: 识别数字。
* 机器学习（machine learning）: 机器学习是最基础的（当下初创公司和研究实验室的热点领域之一）。
* 在90年代初，人们开始意识到一种可以更有效地构建模式识别算法的方法，那就是用数据（可以通过廉价劳动力采集获得）去替换专家（具有很多图像方面知识的人）。
* “机器学习”强调的是，在给计算机程序（或者机器）输入一些数据后，它必须做一些事情，那就是学习这些数据，而这个学习的步骤是明确的。
* 机器学习（Machine Learning）是一门专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身性能的学科。
* 深度学习（deep learning）: 深度学习是非常崭新和有影响力的前沿领域，我们甚至不会去思考-后深度学习时代。
* 深度学习是机器学习研究中的一个新的领域，其动机在于建立、模拟人脑进行分析学习的神经网络，它模仿人脑的机制来解释数据，例如图像，声音和文本。
* 参考地址:
* [深度学习 vs 机器学习 vs 模式识别](http://www.csdn.net/article/2015-03-24/2824301)
* [深度学习 百科资料](http://baike.baidu.com/link?url=76P-uA4EBrC3G-I__P1tqeO7eoDS709Kp4wYuHxc7GNkz_xn0NxuAtEohbpey7LUa2zUQLJxvIKUx4bnrEfOmsWLKbDmvG1PCoRkJisMTQka6-QReTrIxdYY3v93f55q)
> 机器学习已应用于多个领域，远远超出大多数人的想象，横跨: 计算机科学、工程技术和统计学等多个学科。
* 搜索引擎: 根据你的搜索点击，优化你下次的搜索结果,是机器学习来帮助搜索引擎判断哪个结果更适合你（也判断哪个广告更适合你）。
* 垃圾邮件: 会自动的过滤垃圾广告邮件到垃圾箱内。
* 超市优惠券: 你会发现，你在购买小孩子尿布的时候，售货员会赠送你一张优惠券可以兑换6罐啤酒。
* 邮局邮寄: 手写软件自动识别寄送贺卡的地址。
* 申请贷款: 通过你最近的金融活动信息进行综合评定，决定你是否合格。
## 机器学习 组成
### 主要任务
* 分类（classification）: 将实例数据划分到合适的类别中。
* 应用实例: 判断网站是否被黑客入侵（二分类 ），手写数字的自动识别（多分类）
* 回归（regression）: 主要用于预测数值型数据。
* 应用实例: 股票价格波动的预测，房屋价格的预测等。
### 监督学习（supervised learning）
* 必须确定目标变量的值，以便机器学习算法可以发现特征和目标变量之间的关系。在监督学习中，给定一组数据，我们知道正确的输出结果应该是什么样子，并且知道在输入和输出之间有着一个特定的关系。 (包括: 分类和回归)
* 样本集: 训练数据 + 测试数据
* 训练样本 = 特征(feature) + 目标变量(label: 分类-离散值/回归-连续值)
* 特征通常是训练样本集的列，它们是独立测量得到的。
* 目标变量: 目标变量是机器学习预测算法的测试结果。
* 在分类算法中目标变量的类型通常是标称型(如: 真与假)，而在回归算法中通常是连续型(如: 1~100)。
* 监督学习需要注意的问题:
* 偏置方差权衡
* 功能的复杂性和数量的训练数据
* 输入空间的维数
* 噪声中的输出值
* `知识表示`:
* 可以采用规则集的形式【例如: 数学成绩大于90分为优秀】
* 可以采用概率分布的形式【例如: 通过统计分布发现，90%的同学数学成绩，在70分以下，那么大于70分定为优秀】
* 可以使用训练样本集中的一个实例【例如: 通过样本集合，我们训练出一个模型实例，得出 年轻，数学成绩中高等，谈吐优雅，我们认为是优秀】
### 非监督学习（unsupervised learning）
* 在机器学习，无监督学习的问题是，在未加标签的数据中，试图找到隐藏的结构。因为提供给学习者的实例是未标记的，因此没有错误或报酬信号来评估潜在的解决方案。
* 无监督学习是密切相关的统计数据密度估计的问题。然而无监督学习还包括寻求，总结和解释数据的主要特点等诸多技术。在无监督学习使用的许多方法是基于用于处理数据的数据挖掘方法。
* 数据没有类别信息，也不会给定目标值。
* 非监督学习包括的类型:
* 聚类: 在无监督学习中，将数据集分成由类似的对象组成多个类的过程称为聚类。
* 密度估计: 通过样本分布的紧密程度，来估计与分组的相似性。
* 此外，无监督学习还可以减少数据特征的维度，以便我们可以使用二维或三维图形更加直观地展示数据信息。
### 强化学习
这个算法可以训练程序做出某一决定。程序在某一情况下尝试所有的可能行动，记录不同行动的结果并试着找出最好的一次尝试来做决定。 属于这一类算法的有马尔可夫决策过程。
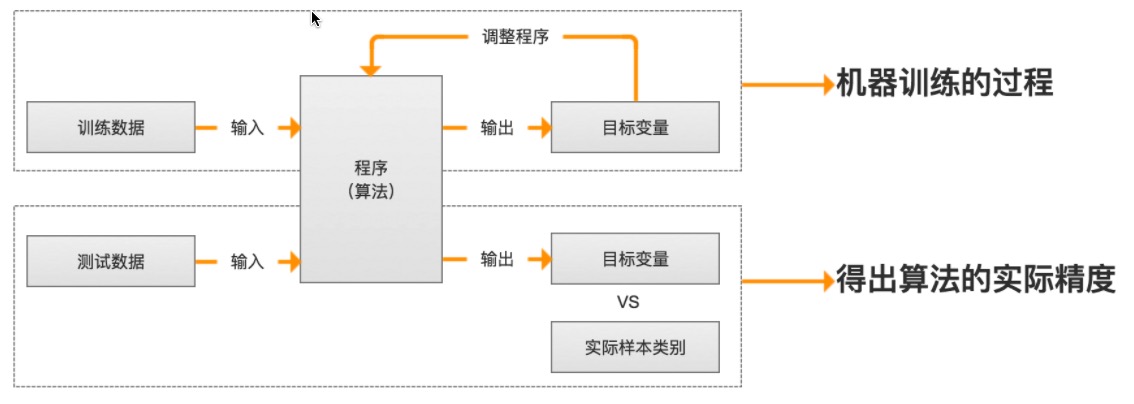
### 训练过程
![机器学习训练过程图](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/机器学习基础训练过程.jpg)
### 算法汇总
![算法汇总](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/ml_algorithm.jpg)
## 机器学习 使用
> 选择算法需要考虑的两个问题
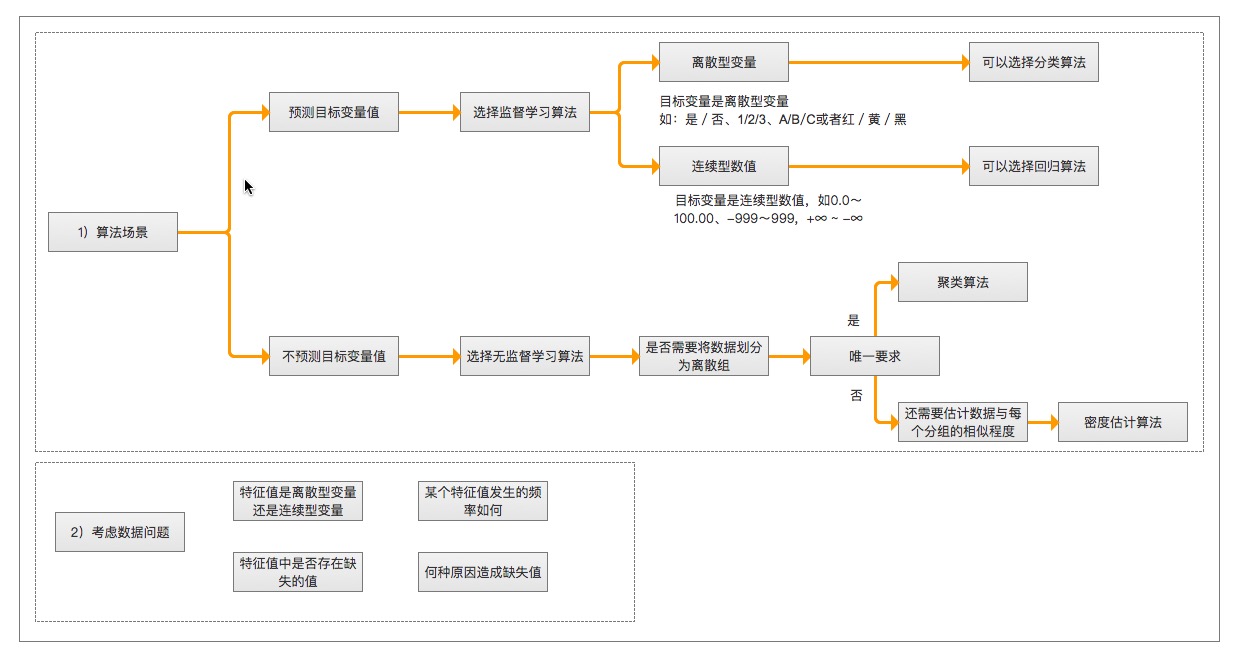
1. 算法场景
* 预测明天是否下雨，因为可以用历史的天气情况做预测，所以选择监督学习算法
* 给一群陌生的人进行分组，但是我们并没有这些人的类别信息，所以选择无监督学习算法、通过他们身高、体重等特征进行处理。
2. 需要收集或分析的数据是什么
> 举例
![选择算法图](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/机器学习基础-选择算法.jpg)
> 机器学习 开发流程
1. 收集数据: 收集样本数据
2. 准备数据: 注意数据的格式
3. 分析数据: 为了确保数据集中没有垃圾数据；
* 如果是算法可以处理的数据格式或可信任的数据源，则可以跳过该步骤；
* 另外该步骤需要人工干预，会降低自动化系统的价值。
4. 训练算法: [机器学习算法核心]如果使用无监督学习算法，由于不存在目标变量值，则可以跳过该步骤
5. 测试算法: [机器学习算法核心]评估算法效果
6. 使用算法: 将机器学习算法转为应用程序
## 机器学习 数学基础
* 微积分
* 统计学/概率论
* 线性代数
## 机器学习 工具
### Python语言
1. 可执行伪代码
2. Python比较流行: 使用广泛、代码范例多、丰富模块库，开发周期短
3. Python语言的特色: 清晰简练、易于理解
4. Python语言的缺点: 唯一不足的是性能问题
5. Python相关的库
* 科学函数库: `SciPy`、`NumPy`(底层语言: C和Fortran)
* 绘图工具库: `Matplotlib`
* 数据分析库 `Pandas`
### 数学工具
* Matlab
## 附: 机器学习专业术语
* 模型（model）: 计算机层面的认知
* 学习算法（learning algorithm），从数据中产生模型的方法
* 数据集（data set）: 一组记录的合集
* 示例（instance）: 对于某个对象的描述
* 样本（sample）: 也叫示例
* 属性（attribute）: 对象的某方面表现或特征
* 特征（feature）: 同属性
* 属性值（attribute value）: 属性上的取值
* 属性空间（attribute space）: 属性张成的空间
* 样本空间/输入空间（samplespace）: 同属性空间
* 特征向量（feature vector）: 在属性空间里每个点对应一个坐标向量，把一个示例称作特征向量
* 维数（dimensionality）: 描述样本参数的个数（也就是空间是几维的）
* 学习（learning）/训练（training）: 从数据中学得模型
* 训练数据（training data）: 训练过程中用到的数据
* 训练样本（training sample）:训练用到的每个样本
* 训练集（training set）: 训练样本组成的集合
* 假设（hypothesis）: 学习模型对应了关于数据的某种潜在规则
* 真相（ground-truth）:真正存在的潜在规律
* 学习器（learner）: 模型的另一种叫法，把学习算法在给定数据和参数空间的实例化
* 预测（prediction）: 判断一个东西的属性
* 标记（label）: 关于示例的结果信息，比如我是一个“好人”。
* 样例（example）: 拥有标记的示例
* 标记空间/输出空间（label space）: 所有标记的集合
* 分类（classification）: 预测是离散值，比如把人分为好人和坏人之类的学习任务
* 回归（regression）: 预测值是连续值，比如你的好人程度达到了0.9，0.6之类的
* 二分类（binary classification）: 只涉及两个类别的分类任务
* 正类（positive class）: 二分类里的一个
* 反类（negative class）: 二分类里的另外一个
* 多分类（multi-class classification）: 涉及多个类别的分类
* 测试（testing）: 学习到模型之后对样本进行预测的过程
* 测试样本（testing sample）: 被预测的样本
* 聚类（clustering）: 把训练集中的对象分为若干组
* 簇（cluster）: 每一个组叫簇
* 监督学习（supervised learning）: 典范--分类和回归
* 无监督学习（unsupervised learning）: 典范--聚类
* 未见示例（unseen instance）: “新样本“，没训练过的样本
* 泛化（generalization）能力: 学得的模型适用于新样本的能力
* 分布（distribution）: 样本空间的全体样本服从的一种规律
* 独立同分布（independent and identically distributed，简称i,i,d.）:获得的每个样本都是独立地从这个分布上采样获得的。
## 机器学习基础补充
### 数据集的划分
* 训练集（Training set） —— 学习样本数据集，通过匹配一些参数来建立一个模型，主要用来训练模型。类比考研前做的解题大全。
* 验证集（validation set） —— 对学习出来的模型，调整模型的参数，如在神经网络中选择隐藏单元数。验证集还用来确定网络结构或者控制模型复杂程度的参数。类比 考研之前做的模拟考试。
* 测试集（Test set） —— 测试训练好的模型的分辨能力。类比 考研。这次真的是一考定终身。
### 模型拟合程度
* 欠拟合（Underfitting）: 模型没有很好地捕捉到数据特征，不能够很好地拟合数据，对训练样本的一般性质尚未学好。类比，光看书不做题觉得自己什么都会了，上了考场才知道自己啥都不会。
* 过拟合（Overfitting）: 模型把训练样本学习“太好了”，可能把一些训练样本自身的特性当做了所有潜在样本都有的一般性质，导致泛化能力下降。类比，做课后题全都做对了，超纲题也都认为是考试必考题目，上了考场还是啥都不会。
通俗来说，欠拟合和过拟合都可以用一句话来说，欠拟合就是: “你太天真了！”，过拟合就是: “你想太多了！”。
### 常见的模型指标
* 正确率 —— 提取出的正确信息条数 / 提取出的信息条数
* 召回率 —— 提取出的正确信息条数 / 样本中的信息条数
* F 值 —— 正确率 * 召回率 * 2 / （正确率 + 召回率）（F值即为正确率和召回率的调和平均值）
举个例子如下:
举个例子如下:
某池塘有 1400 条鲤鱼，300 只虾，300 只乌龟。现在以捕鲤鱼为目的。撒了一张网，逮住了 700 条鲤鱼，200 只
虾， 100 只乌龟。那么这些指标分别如下:
正确率 = 700 / (700 + 200 + 100) = 70%
召回率 = 700 / 1400 = 50%
F 值 = 70% * 50% * 2 / (70% + 50%) = 58.3%
### 模型
* 分类问题 —— 说白了就是将一些未知类别的数据分到现在已知的类别中去。比如，根据你的一些信息，判断你是高富帅，还是穷屌丝。评判分类效果好坏的三个指标就是上面介绍的三个指标: 正确率，召回率，F值。
* 回归问题 —— 对数值型连续随机变量进行预测和建模的监督学习算法。回归往往会通过计算 误差（Error）来确定模型的精确性。
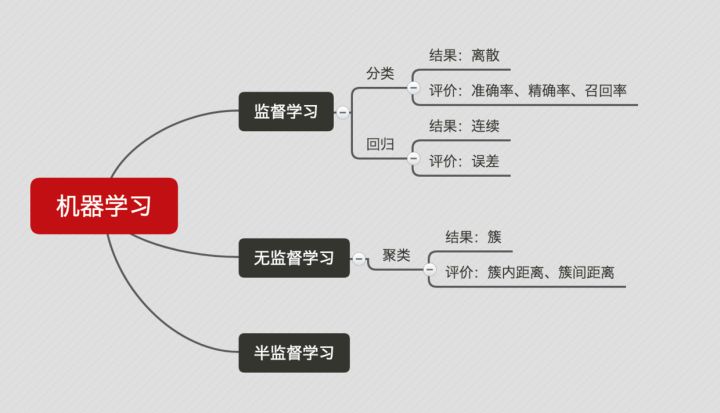
* 聚类问题 —— 聚类是一种无监督学习任务，该算法基于数据的内部结构寻找观察样本的自然族群（即集群）。聚类问题的标准一般基于距离: 簇内距离（Intra-cluster Distance） 和 簇间距离（Inter-cluster Distance） 。簇内距离是越小越好，也就是簇内的元素越相似越好；而簇间距离越大越好，也就是说簇间（不同簇）元素越不相同越好。一般的，衡量聚类问题会给出一个结合簇内距离和簇间距离的公式。
下面这个图可以比较直观地展示出来:
![](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/ml_add_1.jpg)
### 特征工程的一些小东西
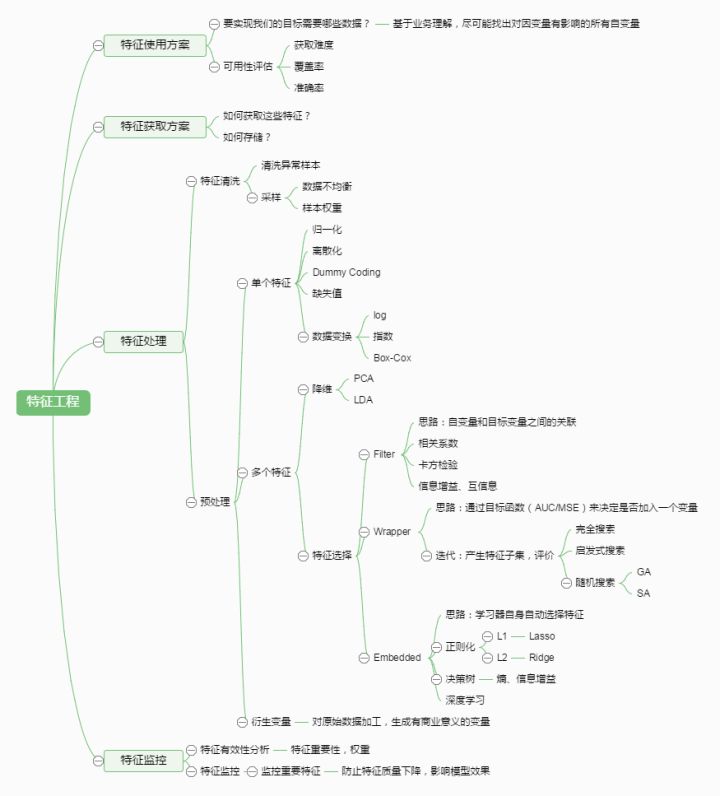
* 特征选择 —— 也叫特征子集选择（FSS，Feature Subset Selection）。是指从已有的 M 个特征（Feature）中选择 N 个特征使得系统的特定指标最优化，是从原始特征中选择出一些最有效特征以降低数据集维度的过程，是提高算法性能的一个重要手段，也是模式识别中关键的数据预处理步骤。
* 特征提取 —— 特征提取是计算机视觉和图像处理中的一个概念。它指的是使用计算机提取图像信息，决定每个图像的点是否属于一个图像特征。特征提取的结果是把图像上的点分为不同的子集，这些子集往往属于孤立的点，连续的曲线或者连续的区域。
下面给出一个特征工程的图:
![](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/ml_add_2.jpg)
### 其他
* Learning rate —— 学习率，通俗地理解，可以理解为步长，步子大了，很容易错过最佳结果。就是本来目标尽在咫尺，可是因为我迈的步子很大，却一下子走过了。步子小了呢，就是同样的距离，我却要走很多很多步，这样导致训练的耗时费力还不讨好。
* 一个总结的知识点很棒的链接 : https://zhuanlan.zhihu.com/p/25197792
* * *
* **作者: [片刻](http://cwiki.apachecn.org/display/~jiangzhonglian) [1988](http://cwiki.apachecn.org/display/~lihuisong)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**
# 第1章 机器学习基础
![机器学习基础_首页](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/机器学习基础-首页.jpg)
## 机器学习 概述
`机器学习(Machine Learning,ML)` 是使用计算机来彰显数据背后的真实含义，它为了把无序的数据转换成有用的信息。是一门多领域交叉学科，涉及概率论、统计学、逼近论、凸分析、算法复杂度理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。
它是人工智能的核心，是使计算机具有智能的根本途径，其应用遍及人工智能的各个领域，它主要使用归纳、综合而不是演绎。
1. 海量的数据
2. 获取有用的信息
## 机器学习 研究意义
机器学习是一门人工智能的科学，该领域的主要研究对象是人工智能，特别是如何在经验学习中改善具体算法的性能”。 “机器学习是对能通过经验自动改进的计算机算法的研究”。 “机器学习是用数据或以往的经验，以此优化计算机程序的性能标准。” 一种经常引用的英文定义是: A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.
机器学习已经有了十分广泛的应用，例如: 数据挖掘、计算机视觉、自然语言处理、生物特征识别、搜索引擎、医学诊断、检测信用卡欺诈、证券市场分析、DNA序列测序、语音和手写识别、战略游戏和机器人运用。
## 机器学习 场景
* 例如: 识别动物猫
* 模式识别（官方标准）: 人们通过大量的经验，得到结论，从而判断它就是猫。
* 机器学习（数据学习）: 人们通过阅读进行学习，观察它会叫、小眼睛、两只耳朵、四条腿、一条尾巴，得到结论，从而判断它就是猫。
* 深度学习（深入数据）: 人们通过深入了解它，发现它会'喵喵'的叫、与同类的猫科动物很类似，得到结论，从而判断它就是猫。（深度学习常用领域: 语音识别、图像识别）
* 模式识别（pattern recognition）: 模式识别是最古老的（作为一个术语而言，可以说是很过时的）。
* 我们把环境与客体统称为“模式”，识别是对模式的一种认知，是如何让一个计算机程序去做一些看起来很“智能”的事情。
* 通过融于智慧和直觉后，通过构建程序，识别一些事物，而不是人，例如: 识别数字。
* 机器学习（machine learning）: 机器学习是最基础的（当下初创公司和研究实验室的热点领域之一）。
* 在90年代初，人们开始意识到一种可以更有效地构建模式识别算法的方法，那就是用数据（可以通过廉价劳动力采集获得）去替换专家（具有很多图像方面知识的人）。
* “机器学习”强调的是，在给计算机程序（或者机器）输入一些数据后，它必须做一些事情，那就是学习这些数据，而这个学习的步骤是明确的。
* 机器学习（Machine Learning）是一门专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身性能的学科。
* 深度学习（deep learning）: 深度学习是非常崭新和有影响力的前沿领域，我们甚至不会去思考-后深度学习时代。
* 深度学习是机器学习研究中的一个新的领域，其动机在于建立、模拟人脑进行分析学习的神经网络，它模仿人脑的机制来解释数据，例如图像，声音和文本。
* 参考地址:
* [深度学习 vs 机器学习 vs 模式识别](http://www.csdn.net/article/2015-03-24/2824301)
* [深度学习 百科资料](http://baike.baidu.com/link?url=76P-uA4EBrC3G-I__P1tqeO7eoDS709Kp4wYuHxc7GNkz_xn0NxuAtEohbpey7LUa2zUQLJxvIKUx4bnrEfOmsWLKbDmvG1PCoRkJisMTQka6-QReTrIxdYY3v93f55q)
> 机器学习已应用于多个领域，远远超出大多数人的想象，横跨: 计算机科学、工程技术和统计学等多个学科。
* 搜索引擎: 根据你的搜索点击，优化你下次的搜索结果,是机器学习来帮助搜索引擎判断哪个结果更适合你（也判断哪个广告更适合你）。
* 垃圾邮件: 会自动的过滤垃圾广告邮件到垃圾箱内。
* 超市优惠券: 你会发现，你在购买小孩子尿布的时候，售货员会赠送你一张优惠券可以兑换6罐啤酒。
* 邮局邮寄: 手写软件自动识别寄送贺卡的地址。
* 申请贷款: 通过你最近的金融活动信息进行综合评定，决定你是否合格。
## 机器学习 组成
### 主要任务
* 分类（classification）: 将实例数据划分到合适的类别中。
* 应用实例: 判断网站是否被黑客入侵（二分类 ），手写数字的自动识别（多分类）
* 回归（regression）: 主要用于预测数值型数据。
* 应用实例: 股票价格波动的预测，房屋价格的预测等。
### 监督学习（supervised learning）
* 必须确定目标变量的值，以便机器学习算法可以发现特征和目标变量之间的关系。在监督学习中，给定一组数据，我们知道正确的输出结果应该是什么样子，并且知道在输入和输出之间有着一个特定的关系。 (包括: 分类和回归)
* 样本集: 训练数据 + 测试数据
* 训练样本 = 特征(feature) + 目标变量(label: 分类-离散值/回归-连续值)
* 特征通常是训练样本集的列，它们是独立测量得到的。
* 目标变量: 目标变量是机器学习预测算法的测试结果。
* 在分类算法中目标变量的类型通常是标称型(如: 真与假)，而在回归算法中通常是连续型(如: 1~100)。
* 监督学习需要注意的问题:
* 偏置方差权衡
* 功能的复杂性和数量的训练数据
* 输入空间的维数
* 噪声中的输出值
* `知识表示`:
* 可以采用规则集的形式【例如: 数学成绩大于90分为优秀】
* 可以采用概率分布的形式【例如: 通过统计分布发现，90%的同学数学成绩，在70分以下，那么大于70分定为优秀】
* 可以使用训练样本集中的一个实例【例如: 通过样本集合，我们训练出一个模型实例，得出 年轻，数学成绩中高等，谈吐优雅，我们认为是优秀】
### 非监督学习（unsupervised learning）
* 在机器学习，无监督学习的问题是，在未加标签的数据中，试图找到隐藏的结构。因为提供给学习者的实例是未标记的，因此没有错误或报酬信号来评估潜在的解决方案。
* 无监督学习是密切相关的统计数据密度估计的问题。然而无监督学习还包括寻求，总结和解释数据的主要特点等诸多技术。在无监督学习使用的许多方法是基于用于处理数据的数据挖掘方法。
* 数据没有类别信息，也不会给定目标值。
* 非监督学习包括的类型:
* 聚类: 在无监督学习中，将数据集分成由类似的对象组成多个类的过程称为聚类。
* 密度估计: 通过样本分布的紧密程度，来估计与分组的相似性。
* 此外，无监督学习还可以减少数据特征的维度，以便我们可以使用二维或三维图形更加直观地展示数据信息。
### 强化学习
这个算法可以训练程序做出某一决定。程序在某一情况下尝试所有的可能行动，记录不同行动的结果并试着找出最好的一次尝试来做决定。 属于这一类算法的有马尔可夫决策过程。
### 训练过程
![机器学习训练过程图](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/机器学习基础训练过程.jpg)
### 算法汇总
![算法汇总](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/ml_algorithm.jpg)
## 机器学习 使用
> 选择算法需要考虑的两个问题
1. 算法场景
* 预测明天是否下雨，因为可以用历史的天气情况做预测，所以选择监督学习算法
* 给一群陌生的人进行分组，但是我们并没有这些人的类别信息，所以选择无监督学习算法、通过他们身高、体重等特征进行处理。
2. 需要收集或分析的数据是什么
> 举例
![选择算法图](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/机器学习基础-选择算法.jpg)
> 机器学习 开发流程
1. 收集数据: 收集样本数据
2. 准备数据: 注意数据的格式
3. 分析数据: 为了确保数据集中没有垃圾数据；
* 如果是算法可以处理的数据格式或可信任的数据源，则可以跳过该步骤；
* 另外该步骤需要人工干预，会降低自动化系统的价值。
4. 训练算法: [机器学习算法核心]如果使用无监督学习算法，由于不存在目标变量值，则可以跳过该步骤
5. 测试算法: [机器学习算法核心]评估算法效果
6. 使用算法: 将机器学习算法转为应用程序
## 机器学习 数学基础
* 微积分
* 统计学/概率论
* 线性代数
## 机器学习 工具
### Python语言
1. 可执行伪代码
2. Python比较流行: 使用广泛、代码范例多、丰富模块库，开发周期短
3. Python语言的特色: 清晰简练、易于理解
4. Python语言的缺点: 唯一不足的是性能问题
5. Python相关的库
* 科学函数库: `SciPy`、`NumPy`(底层语言: C和Fortran)
* 绘图工具库: `Matplotlib`
* 数据分析库 `Pandas`
### 数学工具
* Matlab
## 附: 机器学习专业术语
* 模型（model）: 计算机层面的认知
* 学习算法（learning algorithm），从数据中产生模型的方法
* 数据集（data set）: 一组记录的合集
* 示例（instance）: 对于某个对象的描述
* 样本（sample）: 也叫示例
* 属性（attribute）: 对象的某方面表现或特征
* 特征（feature）: 同属性
* 属性值（attribute value）: 属性上的取值
* 属性空间（attribute space）: 属性张成的空间
* 样本空间/输入空间（samplespace）: 同属性空间
* 特征向量（feature vector）: 在属性空间里每个点对应一个坐标向量，把一个示例称作特征向量
* 维数（dimensionality）: 描述样本参数的个数（也就是空间是几维的）
* 学习（learning）/训练（training）: 从数据中学得模型
* 训练数据（training data）: 训练过程中用到的数据
* 训练样本（training sample）:训练用到的每个样本
* 训练集（training set）: 训练样本组成的集合
* 假设（hypothesis）: 学习模型对应了关于数据的某种潜在规则
* 真相（ground-truth）:真正存在的潜在规律
* 学习器（learner）: 模型的另一种叫法，把学习算法在给定数据和参数空间的实例化
* 预测（prediction）: 判断一个东西的属性
* 标记（label）: 关于示例的结果信息，比如我是一个“好人”。
* 样例（example）: 拥有标记的示例
* 标记空间/输出空间（label space）: 所有标记的集合
* 分类（classification）: 预测是离散值，比如把人分为好人和坏人之类的学习任务
* 回归（regression）: 预测值是连续值，比如你的好人程度达到了0.9，0.6之类的
* 二分类（binary classification）: 只涉及两个类别的分类任务
* 正类（positive class）: 二分类里的一个
* 反类（negative class）: 二分类里的另外一个
* 多分类（multi-class classification）: 涉及多个类别的分类
* 测试（testing）: 学习到模型之后对样本进行预测的过程
* 测试样本（testing sample）: 被预测的样本
* 聚类（clustering）: 把训练集中的对象分为若干组
* 簇（cluster）: 每一个组叫簇
* 监督学习（supervised learning）: 典范--分类和回归
* 无监督学习（unsupervised learning）: 典范--聚类
* 未见示例（unseen instance）: “新样本“，没训练过的样本
* 泛化（generalization）能力: 学得的模型适用于新样本的能力
* 分布（distribution）: 样本空间的全体样本服从的一种规律
* 独立同分布（independent and identically distributed，简称i,i,d.）:获得的每个样本都是独立地从这个分布上采样获得的。
## 机器学习基础补充
### 数据集的划分
* 训练集（Training set） —— 学习样本数据集，通过匹配一些参数来建立一个模型，主要用来训练模型。类比考研前做的解题大全。
* 验证集（validation set） —— 对学习出来的模型，调整模型的参数，如在神经网络中选择隐藏单元数。验证集还用来确定网络结构或者控制模型复杂程度的参数。类比 考研之前做的模拟考试。
* 测试集（Test set） —— 测试训练好的模型的分辨能力。类比 考研。这次真的是一考定终身。
### 模型拟合程度
* 欠拟合（Underfitting）: 模型没有很好地捕捉到数据特征，不能够很好地拟合数据，对训练样本的一般性质尚未学好。类比，光看书不做题觉得自己什么都会了，上了考场才知道自己啥都不会。
* 过拟合（Overfitting）: 模型把训练样本学习“太好了”，可能把一些训练样本自身的特性当做了所有潜在样本都有的一般性质，导致泛化能力下降。类比，做课后题全都做对了，超纲题也都认为是考试必考题目，上了考场还是啥都不会。
通俗来说，欠拟合和过拟合都可以用一句话来说，欠拟合就是: “你太天真了！”，过拟合就是: “你想太多了！”。
### 常见的模型指标
* 正确率 —— 提取出的正确信息条数 / 提取出的信息条数
* 召回率 —— 提取出的正确信息条数 / 样本中的信息条数
* F 值 —— 正确率 * 召回率 * 2 / （正确率 + 召回率）（F值即为正确率和召回率的调和平均值）
举个例子如下:
举个例子如下:
某池塘有 1400 条鲤鱼，300 只虾，300 只乌龟。现在以捕鲤鱼为目的。撒了一张网，逮住了 700 条鲤鱼，200 只
虾， 100 只乌龟。那么这些指标分别如下:
正确率 = 700 / (700 + 200 + 100) = 70%
召回率 = 700 / 1400 = 50%
F 值 = 70% * 50% * 2 / (70% + 50%) = 58.3%
### 模型
* 分类问题 —— 说白了就是将一些未知类别的数据分到现在已知的类别中去。比如，根据你的一些信息，判断你是高富帅，还是穷屌丝。评判分类效果好坏的三个指标就是上面介绍的三个指标: 正确率，召回率，F值。
* 回归问题 —— 对数值型连续随机变量进行预测和建模的监督学习算法。回归往往会通过计算 误差（Error）来确定模型的精确性。
* 聚类问题 —— 聚类是一种无监督学习任务，该算法基于数据的内部结构寻找观察样本的自然族群（即集群）。聚类问题的标准一般基于距离: 簇内距离（Intra-cluster Distance） 和 簇间距离（Inter-cluster Distance） 。簇内距离是越小越好，也就是簇内的元素越相似越好；而簇间距离越大越好，也就是说簇间（不同簇）元素越不相同越好。一般的，衡量聚类问题会给出一个结合簇内距离和簇间距离的公式。
下面这个图可以比较直观地展示出来:
![](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/ml_add_1.jpg)
### 特征工程的一些小东西
* 特征选择 —— 也叫特征子集选择（FSS，Feature Subset Selection）。是指从已有的 M 个特征（Feature）中选择 N 个特征使得系统的特定指标最优化，是从原始特征中选择出一些最有效特征以降低数据集维度的过程，是提高算法性能的一个重要手段，也是模式识别中关键的数据预处理步骤。
* 特征提取 —— 特征提取是计算机视觉和图像处理中的一个概念。它指的是使用计算机提取图像信息，决定每个图像的点是否属于一个图像特征。特征提取的结果是把图像上的点分为不同的子集，这些子集往往属于孤立的点，连续的曲线或者连续的区域。
下面给出一个特征工程的图:
![](http://data.apachecn.org/img/AiLearning/ml/1.MLFoundation/ml_add_2.jpg)
### 其他
* Learning rate —— 学习率，通俗地理解，可以理解为步长，步子大了，很容易错过最佳结果。就是本来目标尽在咫尺，可是因为我迈的步子很大，却一下子走过了。步子小了呢，就是同样的距离，我却要走很多很多步，这样导致训练的耗时费力还不讨好。
* 一个总结的知识点很棒的链接 : https://zhuanlan.zhihu.com/p/25197792
* * *
* **作者: [片刻](http://cwiki.apachecn.org/display/~jiangzhonglian) [1988](http://cwiki.apachecn.org/display/~lihuisong)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**

490
docs/ml/10.KMeans聚类.md → docs/ml/10.md
View File

@@ -1,246 +1,246 @@
# 第 10 章 K-Means（K-均值）聚类算法
![K-Means（K-均值）聚类算法_首页](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/K-Means_首页.jpg)
## 聚类
聚类，简单来说，就是将一个庞杂数据集中具有相似特征的数据自动归类到一起，称为一个簇，簇内的对象越相似，聚类的效果越好。它是一种无监督的学习(Unsupervised Learning)方法,不需要预先标注好的训练集。聚类与分类最大的区别就是分类的目标事先已知，例如猫狗识别，你在分类之前已经预先知道要将它分为猫、狗两个种类；而在你聚类之前，你对你的目标是未知的，同样以动物为例，对于一个动物集来说，你并不清楚这个数据集内部有多少种类的动物，你能做的只是利用聚类方法将它自动按照特征分为多类，然后人为给出这个聚类结果的定义（即簇识别）。例如，你将一个动物集分为了三簇（类），然后通过观察这三类动物的特征，你为每一个簇起一个名字，如大象、狗、猫等，这就是聚类的基本思想。
至于“相似”这一概念，是利用距离这个评价标准来衡量的，我们通过计算对象与对象之间的距离远近来判断它们是否属于同一类别，即是否是同一个簇。至于距离如何计算，科学家们提出了许多种距离的计算方法，其中欧式距离是最为简单和常用的，除此之外还有曼哈顿距离和余弦相似性距离等。
欧式距离，我想大家再熟悉不过了，但为免有一些基础薄弱的同学，在此再说明一下，它的定义为:
对于x点坐标为(x1,x2,x3,...,xn)和 y点坐标为(y1,y2,y3,...,yn)，两者的欧式距离为:
$$
d(x,y)
={\sqrt{
(x_{1}-y_{1})^{2}+(x_{2}-y_{2})^{2} + \cdots +(x_{n}-y_{n})^{2}
}}
={\sqrt{
\sum_{ {i=1} }^{n}(x_{i}-y_{i})^{2}
}}
$$
在二维平面，它就是我们初中时就学过的两点距离公式
## K-Means 算法
K-Means 是发现给定数据集的 K 个簇的聚类算法, 之所以称之为 `K-均值` 是因为它可以发现 K 个不同的簇, 且每个簇的中心采用簇中所含值的均值计算而成.
簇个数 K 是用户指定的, 每一个簇通过其质心（centroid）, 即簇中所有点的中心来描述.
聚类与分类算法的最大区别在于, 分类的目标类别已知, 而聚类的目标类别是未知的.
**优点**:
* 属于无监督学习，无须准备训练集
* 原理简单，实现起来较为容易
* 结果可解释性较好
**缺点**:
* **需手动设置k值**。 在算法开始预测之前，我们需要手动设置k值，即估计数据大概的类别个数，不合理的k值会使结果缺乏解释性
* 可能收敛到局部最小值, 在大规模数据集上收敛较慢
* 对于异常点、离群点敏感
使用数据类型 : 数值型数据
### K-Means 场景
kmeans，如前所述，用于数据集内种类属性不明晰，希望能够通过数据挖掘出或自动归类出有相似特点的对象的场景。其商业界的应用场景一般为挖掘出具有相似特点的潜在客户群体以便公司能够重点研究、对症下药。
例如，在2000年和2004年的美国总统大选中，候选人的得票数比较接近或者说非常接近。任一候选人得到的普选票数的最大百分比为50.7%而最小百分比为47.9% 如果1%的选民将手中的选票投向另外的候选人，那么选举结果就会截然不同。 实际上，如果妥善加以引导与吸引，少部分选民就会转换立场。尽管这类选举者占的比例较低，但当候选人的选票接近时，这些人的立场无疑会对选举结果产生非常大的影响。如何找出这类选民，以及如何在有限的预算下采取措施来吸引他们？ 答案就是聚类（Clustering)。
那么，具体如何实施呢？首先，收集用户的信息，可以同时收集用户满意或不满意的信息，这是因为任何对用户重要的内容都可能影响用户的投票结果。然后，将这些信息输入到某个聚类算法中。接着，对聚类结果中的每一个簇（最好选择最大簇 ）， 精心构造能够吸引该簇选民的消息。最后， 开展竞选活动并观察上述做法是否有效。
另一个例子就是产品部门的市场调研了。为了更好的了解自己的用户，产品部门可以采用聚类的方法得到不同特征的用户群体，然后针对不同的用户群体可以对症下药，为他们提供更加精准有效的服务。
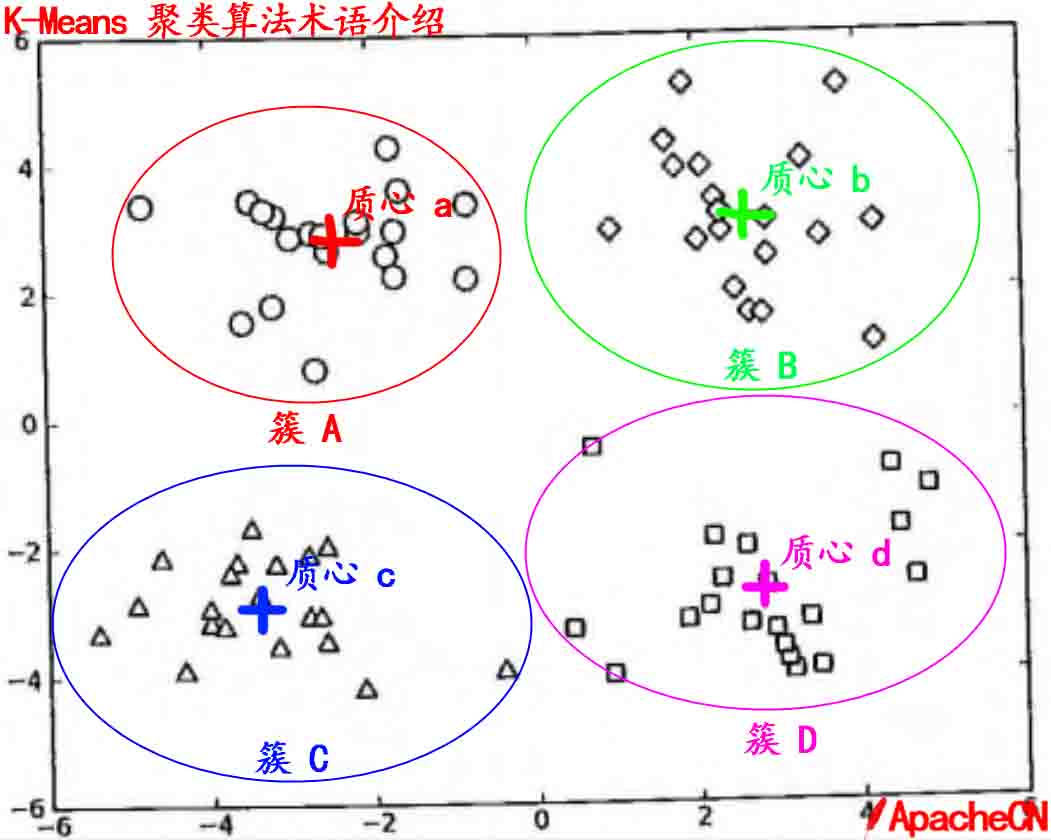
### K-Means 术语
* 簇: 所有数据的点集合，簇中的对象是相似的。
* 质心: 簇中所有点的中心（计算所有点的均值而来）.
* SSE: Sum of Sqared Error（误差平方和）, 它被用来评估模型的好坏，SSE 值越小，表示越接近它们的质心. 聚类效果越好。由于对误差取了平方，因此更加注重那些远离中心的点（一般为边界点或离群点）。详情见kmeans的评价标准。
有关 `簇` 和 `质心` 术语更形象的介绍, 请参考下图:
![K-Means 术语图](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/apachecn-k-means-term-1.jpg)
### K-Means 工作流程
1. 首先, 随机确定 K 个初始点作为质心（**不必是数据中的点**）。
2. 然后将数据集中的每个点分配到一个簇中, 具体来讲, 就是为每个点找到距其最近的质心, 并将其分配该质心所对应的簇. 这一步完成之后, 每个簇的质心更新为该簇所有点的平均值.
3.重复上述过程直到数据集中的所有点都距离它所对应的质心最近时结束。
上述过程的 `伪代码` 如下:
* 创建 k 个点作为起始质心（通常是随机选择）
* 当任意一个点的簇分配结果发生改变时（不改变时算法结束）
* 对数据集中的每个数据点
* 对每个质心
* 计算质心与数据点之间的距离
* 将数据点分配到距其最近的簇
* 对每一个簇, 计算簇中所有点的均值并将均值作为质心
### K-Means 开发流程
```
收集数据: 使用任意方法
准备数据: 需要数值型数据类计算距离, 也可以将标称型数据映射为二值型数据再用于距离计算
分析数据: 使用任意方法
训练算法: 不适用于无监督学习，即无监督学习不需要训练步骤
测试算法: 应用聚类算法、观察结果.可以使用量化的误差指标如误差平方和（后面会介绍）来评价算法的结果.
使用算法: 可以用于所希望的任何应用.通常情况下, 簇质心可以代表整个簇的数据来做出决策.
```
### K-Means 的评价标准
k-means算法因为手动选取k值和初始化随机质心的缘故，每一次的结果不会完全一样，而且由于手动选取k值，我们需要知道我们选取的k值是否合理，聚类效果好不好，那么如何来评价某一次的聚类效果呢？也许将它们画在图上直接观察是最好的办法，但现实是，我们的数据不会仅仅只有两个特征，一般来说都有十几个特征，而观察十几维的空间对我们来说是一个无法完成的任务。因此，我们需要一个公式来帮助我们判断聚类的性能，这个公式就是**SSE** (Sum of Squared Error, 误差平方和 ），它其实就是每一个点到其簇内质心的距离的平方值的总和，这个数值对应kmeans函数中**clusterAssment**矩阵的第一列之和。 **SSE**值越小表示数据点越接近于它们的质心，聚类效果也越好。 因为对误差取了平方，因此更加重视那些远离中心的点。一种肯定可以降低**SSE**值的方法是增加簇的个数，但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。
### K-Means 聚类算法函数
#### 从文件加载数据集
```python
# 从文本中构建矩阵，加载文本文件，然后处理
def loadDataSet(fileName): # 通用函数，用来解析以 tab 键分隔的 floats（浮点数），例如: 1.658985 4.285136
dataMat = []
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = map(float,curLine) # 映射所有的元素为 float（浮点数）类型
dataMat.append(fltLine)
return dataMat
```
#### 计算两个向量的欧氏距离
```python
# 计算两个向量的欧式距离（可根据场景选择其他距离公式）
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) # la.norm(vecA-vecB)
```
#### 构建一个包含 K 个随机质心的集合
```python
# 为给定数据集构建一个包含 k 个随机质心的集合。随机质心必须要在整个数据集的边界之内，这可以通过找到数据集每一维的最小和最大值来完成。然后生成 0~1.0 之间的随机数并通过取值范围和最小值，以便确保随机点在数据的边界之内。
def randCent(dataSet, k):
n = shape(dataSet)[1] # 列的数量，即数据的特征个数
centroids = mat(zeros((k,n))) # 创建k个质心矩阵
for j in range(n): # 创建随机簇质心，并且在每一维的边界内
minJ = min(dataSet[:,j]) # 最小值
rangeJ = float(max(dataSet[:,j]) - minJ) # 范围 = 最大值 - 最小值
centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1)) # 随机生成，mat为numpy函数，需要在最开始写上 from numpy import *
return centroids
```
#### K-Means 聚类算法
```python
# k-means 聚类算法
# 该算法会创建k个质心，然后将每个点分配到最近的质心，再重新计算质心。
# 这个过程重复数次，直到数据点的簇分配结果不再改变位置。
# 运行结果（多次运行结果可能会不一样，可以试试，原因为随机质心的影响，但总的结果是对的， 因为数据足够相似，也可能会陷入局部最小值）
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
m = shape(dataSet)[0] # 行数，即数据个数
clusterAssment = mat(zeros((m, 2))) # 创建一个与 dataSet 行数一样，但是有两列的矩阵，用来保存簇分配结果
centroids = createCent(dataSet, k) # 创建质心，随机k个质心
clusterChanged = True
while clusterChanged:
clusterChanged = False
for i in range(m): # 循环每一个数据点并分配到最近的质心中去
minDist = inf; minIndex = -1
for j in range(k):
distJI = distMeas(centroids[j,:],dataSet[i,:]) # 计算数据点到质心的距离
if distJI < minDist: # 如果距离比 minDist（最小距离）还小，更新 minDist（最小距离）和最小质心的 index（索引）
minDist = distJI; minIndex = j
if clusterAssment[i, 0] != minIndex: # 簇分配结果改变
clusterChanged = True # 簇改变
clusterAssment[i, :] = minIndex,minDist**2 # 更新簇分配结果为最小质心的 index（索引），minDist（最小距离）的平方
print centroids
for cent in range(k): # 更新质心
ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A==cent)[0]] # 获取该簇中的所有点
centroids[cent,:] = mean(ptsInClust, axis=0) # 将质心修改为簇中所有点的平均值，mean 就是求平均值的
return centroids, clusterAssment
```
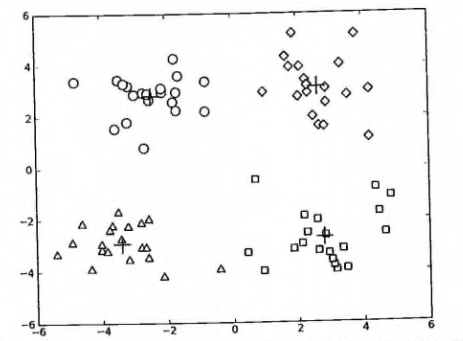
#### 测试函数
1. 测试一下以上的基础函数是否可以如预期运行, 请看: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/10.kmeans/kMeans.py>
2. 测试一下 kMeans 函数是否可以如预期运行, 请看: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/10.kmeans/kMeans.py>
参考运行结果如下:
![K-Means 运行结果1](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/apachecn-k-means-run-result-1.jpg)
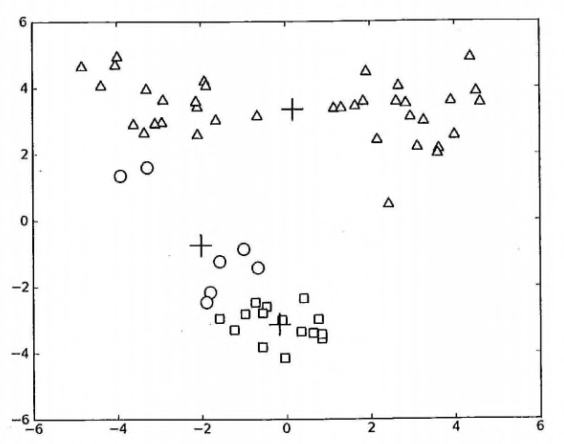
### K-Means 聚类算法的缺陷
> 在 kMeans 的函数测试中，可能偶尔会陷入局部最小值（局部最优的结果，但不是全局最优的结果）.
局部最小值的的情况如下:
![K-Means 局部最小值1](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/apachecn-kmeans-partial-best-result-1.jpg)
出现这个问题有很多原因，可能是k值取的不合适，可能是距离函数不合适，可能是最初随机选取的质心靠的太近，也可能是数据本身分布的问题。
为了解决这个问题，我们可以对生成的簇进行后处理，一种方法是将具有最大**SSE**值的簇划分成两个簇。具体实现时可以将最大簇包含的点过滤出来并在这些点上运行K-均值算法，令k设为2。
为了保持簇总数不变，可以将某两个簇进行合并。从上图中很明显就可以看出，应该将上图下部两个出错的簇质心进行合并。那么问题来了，我们可以很容易对二维数据上的聚类进行可视化， 但是如果遇到40维的数据应该如何去做？
有两种可以量化的办法: 合并最近的质心，或者合并两个使得**SSE**增幅最小的质心。 第一种思路通过计算所有质心之间的距离， 然后合并距离最近的两个点来实现。第二种方法需要合并两个簇然后计算总**SSE**值。必须在所有可能的两个簇上重复上述处理过程，直到找到合并最佳的两个簇为止。
因为上述后处理过程实在是有些繁琐，所以有更厉害的大佬提出了另一个称之为二分K-均值（bisecting K-Means）的算法.
### 二分 K-Means 聚类算法
该算法首先将所有点作为一个簇，然后将该簇一分为二。
之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分时候可以最大程度降低 SSE（平方和误差）的值。
上述基于 SSE 的划分过程不断重复，直到得到用户指定的簇数目为止。
#### 二分 K-Means 聚类算法伪代码
* 将所有点看成一个簇
* 当簇数目小于 k 时
* 对于每一个簇
* 计算总误差
* 在给定的簇上面进行 KMeans 聚类（k=2）
* 计算将该簇一分为二之后的总误差
* 选择使得误差最小的那个簇进行划分操作
另一种做法是选择 SSE 最大的簇进行划分，直到簇数目达到用户指定的数目位置。
接下来主要介绍该做法的python2代码实现
#### 二分 K-Means 聚类算法代码
```python
# 二分 KMeans 聚类算法, 基于 kMeans 基础之上的优化，以避免陷入局部最小值
def biKMeans(dataSet, k, distMeas=distEclud):
m = shape(dataSet)[0]
clusterAssment = mat(zeros((m,2))) # 保存每个数据点的簇分配结果和平方误差
centroid0 = mean(dataSet, axis=0).tolist()[0] # 质心初始化为所有数据点的均值
centList =[centroid0] # 初始化只有 1 个质心的 list
for j in range(m): # 计算所有数据点到初始质心的距离平方误差
clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
while (len(centList) < k): # 当质心数量小于 k 时
lowestSSE = inf
for i in range(len(centList)): # 对每一个质心
ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:] # 获取当前簇 i 下的所有数据点
centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas) # 将当前簇 i 进行二分 kMeans 处理
sseSplit = sum(splitClustAss[:,1]) # 将二分 kMeans 结果中的平方和的距离进行求和
sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1]) # 将未参与二分 kMeans 分配结果中的平方和的距离进行求和
print "sseSplit, and notSplit: ",sseSplit,sseNotSplit
if (sseSplit + sseNotSplit) < lowestSSE: # 总的（未拆分和已拆分）误差和越小，越相似，效果越优化，划分的结果更好（注意: 这里的理解很重要，不明白的地方可以和我们一起讨论）
bestCentToSplit = i
bestNewCents = centroidMat
bestClustAss = splitClustAss.copy()
lowestSSE = sseSplit + sseNotSplit
# 找出最好的簇分配结果
bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) # 调用二分 kMeans 的结果，默认簇是 0,1. 当然也可以改成其它的数字
bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit # 更新为最佳质心
print 'the bestCentToSplit is: ',bestCentToSplit
print 'the len of bestClustAss is: ', len(bestClustAss)
# 更新质心列表
centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0] # 更新原质心 list 中的第 i 个质心为使用二分 kMeans 后 bestNewCents 的第一个质心
centList.append(bestNewCents[1,:].tolist()[0]) # 添加 bestNewCents 的第二个质心
clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss # 重新分配最好簇下的数据（质心）以及SSE
return mat(centList), clusterAssment
```
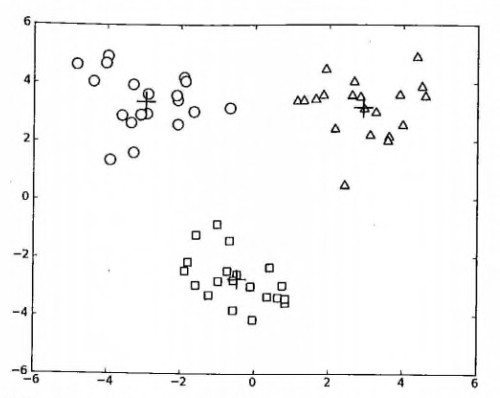
#### 测试二分 KMeans 聚类算法
* 测试一下二分 KMeans 聚类算法，请看: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/10.kmeans/kMeans.py>
上述函数可以运行多次，聚类会收敛到全局最小值，而原始的 kMeans() 函数偶尔会陷入局部最小值。
运行参考结果如下:
![二分 K-Means 运行结果1](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/apachecn-bikmeans-run-result-1.jpg)
* **作者: [那伊抹微笑](http://cwiki.apachecn.org/display/~xuxin), [清都江水郎](http://cwiki.apachecn.org/display/~xuzhaoqing)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
# 第 10 章 K-Means（K-均值）聚类算法
![K-Means（K-均值）聚类算法_首页](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/K-Means_首页.jpg)
## 聚类
聚类，简单来说，就是将一个庞杂数据集中具有相似特征的数据自动归类到一起，称为一个簇，簇内的对象越相似，聚类的效果越好。它是一种无监督的学习(Unsupervised Learning)方法,不需要预先标注好的训练集。聚类与分类最大的区别就是分类的目标事先已知，例如猫狗识别，你在分类之前已经预先知道要将它分为猫、狗两个种类；而在你聚类之前，你对你的目标是未知的，同样以动物为例，对于一个动物集来说，你并不清楚这个数据集内部有多少种类的动物，你能做的只是利用聚类方法将它自动按照特征分为多类，然后人为给出这个聚类结果的定义（即簇识别）。例如，你将一个动物集分为了三簇（类），然后通过观察这三类动物的特征，你为每一个簇起一个名字，如大象、狗、猫等，这就是聚类的基本思想。
至于“相似”这一概念，是利用距离这个评价标准来衡量的，我们通过计算对象与对象之间的距离远近来判断它们是否属于同一类别，即是否是同一个簇。至于距离如何计算，科学家们提出了许多种距离的计算方法，其中欧式距离是最为简单和常用的，除此之外还有曼哈顿距离和余弦相似性距离等。
欧式距离，我想大家再熟悉不过了，但为免有一些基础薄弱的同学，在此再说明一下，它的定义为:
对于x点坐标为(x1,x2,x3,...,xn)和 y点坐标为(y1,y2,y3,...,yn)，两者的欧式距离为:
$$
d(x,y)
={\sqrt{
(x_{1}-y_{1})^{2}+(x_{2}-y_{2})^{2} + \cdots +(x_{n}-y_{n})^{2}
}}
={\sqrt{
\sum_{ {i=1} }^{n}(x_{i}-y_{i})^{2}
}}
$$
在二维平面，它就是我们初中时就学过的两点距离公式
## K-Means 算法
K-Means 是发现给定数据集的 K 个簇的聚类算法, 之所以称之为 `K-均值` 是因为它可以发现 K 个不同的簇, 且每个簇的中心采用簇中所含值的均值计算而成.
簇个数 K 是用户指定的, 每一个簇通过其质心（centroid）, 即簇中所有点的中心来描述.
聚类与分类算法的最大区别在于, 分类的目标类别已知, 而聚类的目标类别是未知的.
**优点**:
* 属于无监督学习，无须准备训练集
* 原理简单，实现起来较为容易
* 结果可解释性较好
**缺点**:
* **需手动设置k值**。 在算法开始预测之前，我们需要手动设置k值，即估计数据大概的类别个数，不合理的k值会使结果缺乏解释性
* 可能收敛到局部最小值, 在大规模数据集上收敛较慢
* 对于异常点、离群点敏感
使用数据类型 : 数值型数据
### K-Means 场景
kmeans，如前所述，用于数据集内种类属性不明晰，希望能够通过数据挖掘出或自动归类出有相似特点的对象的场景。其商业界的应用场景一般为挖掘出具有相似特点的潜在客户群体以便公司能够重点研究、对症下药。
例如，在2000年和2004年的美国总统大选中，候选人的得票数比较接近或者说非常接近。任一候选人得到的普选票数的最大百分比为50.7%而最小百分比为47.9% 如果1%的选民将手中的选票投向另外的候选人，那么选举结果就会截然不同。 实际上，如果妥善加以引导与吸引，少部分选民就会转换立场。尽管这类选举者占的比例较低，但当候选人的选票接近时，这些人的立场无疑会对选举结果产生非常大的影响。如何找出这类选民，以及如何在有限的预算下采取措施来吸引他们？ 答案就是聚类（Clustering)。
那么，具体如何实施呢？首先，收集用户的信息，可以同时收集用户满意或不满意的信息，这是因为任何对用户重要的内容都可能影响用户的投票结果。然后，将这些信息输入到某个聚类算法中。接着，对聚类结果中的每一个簇（最好选择最大簇 ）， 精心构造能够吸引该簇选民的消息。最后， 开展竞选活动并观察上述做法是否有效。
另一个例子就是产品部门的市场调研了。为了更好的了解自己的用户，产品部门可以采用聚类的方法得到不同特征的用户群体，然后针对不同的用户群体可以对症下药，为他们提供更加精准有效的服务。
### K-Means 术语
* 簇: 所有数据的点集合，簇中的对象是相似的。
* 质心: 簇中所有点的中心（计算所有点的均值而来）.
* SSE: Sum of Sqared Error（误差平方和）, 它被用来评估模型的好坏，SSE 值越小，表示越接近它们的质心. 聚类效果越好。由于对误差取了平方，因此更加注重那些远离中心的点（一般为边界点或离群点）。详情见kmeans的评价标准。
有关 `簇` 和 `质心` 术语更形象的介绍, 请参考下图:
![K-Means 术语图](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/apachecn-k-means-term-1.jpg)
### K-Means 工作流程
1. 首先, 随机确定 K 个初始点作为质心（**不必是数据中的点**）。
2. 然后将数据集中的每个点分配到一个簇中, 具体来讲, 就是为每个点找到距其最近的质心, 并将其分配该质心所对应的簇. 这一步完成之后, 每个簇的质心更新为该簇所有点的平均值.
3.重复上述过程直到数据集中的所有点都距离它所对应的质心最近时结束。
上述过程的 `伪代码` 如下:
* 创建 k 个点作为起始质心（通常是随机选择）
* 当任意一个点的簇分配结果发生改变时（不改变时算法结束）
* 对数据集中的每个数据点
* 对每个质心
* 计算质心与数据点之间的距离
* 将数据点分配到距其最近的簇
* 对每一个簇, 计算簇中所有点的均值并将均值作为质心
### K-Means 开发流程
```
收集数据: 使用任意方法
准备数据: 需要数值型数据类计算距离, 也可以将标称型数据映射为二值型数据再用于距离计算
分析数据: 使用任意方法
训练算法: 不适用于无监督学习，即无监督学习不需要训练步骤
测试算法: 应用聚类算法、观察结果.可以使用量化的误差指标如误差平方和（后面会介绍）来评价算法的结果.
使用算法: 可以用于所希望的任何应用.通常情况下, 簇质心可以代表整个簇的数据来做出决策.
```
### K-Means 的评价标准
k-means算法因为手动选取k值和初始化随机质心的缘故，每一次的结果不会完全一样，而且由于手动选取k值，我们需要知道我们选取的k值是否合理，聚类效果好不好，那么如何来评价某一次的聚类效果呢？也许将它们画在图上直接观察是最好的办法，但现实是，我们的数据不会仅仅只有两个特征，一般来说都有十几个特征，而观察十几维的空间对我们来说是一个无法完成的任务。因此，我们需要一个公式来帮助我们判断聚类的性能，这个公式就是**SSE** (Sum of Squared Error, 误差平方和 ），它其实就是每一个点到其簇内质心的距离的平方值的总和，这个数值对应kmeans函数中**clusterAssment**矩阵的第一列之和。 **SSE**值越小表示数据点越接近于它们的质心，聚类效果也越好。 因为对误差取了平方，因此更加重视那些远离中心的点。一种肯定可以降低**SSE**值的方法是增加簇的个数，但这违背了聚类的目标。聚类的目标是在保持簇数目不变的情况下提高簇的质量。
### K-Means 聚类算法函数
#### 从文件加载数据集
```python
# 从文本中构建矩阵，加载文本文件，然后处理
def loadDataSet(fileName): # 通用函数，用来解析以 tab 键分隔的 floats（浮点数），例如: 1.658985 4.285136
dataMat = []
fr = open(fileName)
for line in fr.readlines():
curLine = line.strip().split('\t')
fltLine = map(float,curLine) # 映射所有的元素为 float（浮点数）类型
dataMat.append(fltLine)
return dataMat
```
#### 计算两个向量的欧氏距离
```python
# 计算两个向量的欧式距离（可根据场景选择其他距离公式）
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) # la.norm(vecA-vecB)
```
#### 构建一个包含 K 个随机质心的集合
```python
# 为给定数据集构建一个包含 k 个随机质心的集合。随机质心必须要在整个数据集的边界之内，这可以通过找到数据集每一维的最小和最大值来完成。然后生成 0~1.0 之间的随机数并通过取值范围和最小值，以便确保随机点在数据的边界之内。
def randCent(dataSet, k):
n = shape(dataSet)[1] # 列的数量，即数据的特征个数
centroids = mat(zeros((k,n))) # 创建k个质心矩阵
for j in range(n): # 创建随机簇质心，并且在每一维的边界内
minJ = min(dataSet[:,j]) # 最小值
rangeJ = float(max(dataSet[:,j]) - minJ) # 范围 = 最大值 - 最小值
centroids[:,j] = mat(minJ + rangeJ * random.rand(k,1)) # 随机生成，mat为numpy函数，需要在最开始写上 from numpy import *
return centroids
```
#### K-Means 聚类算法
```python
# k-means 聚类算法
# 该算法会创建k个质心，然后将每个点分配到最近的质心，再重新计算质心。
# 这个过程重复数次，直到数据点的簇分配结果不再改变位置。
# 运行结果（多次运行结果可能会不一样，可以试试，原因为随机质心的影响，但总的结果是对的， 因为数据足够相似，也可能会陷入局部最小值）
def kMeans(dataSet, k, distMeas=distEclud, createCent=randCent):
m = shape(dataSet)[0] # 行数，即数据个数
clusterAssment = mat(zeros((m, 2))) # 创建一个与 dataSet 行数一样，但是有两列的矩阵，用来保存簇分配结果
centroids = createCent(dataSet, k) # 创建质心，随机k个质心
clusterChanged = True
while clusterChanged:
clusterChanged = False
for i in range(m): # 循环每一个数据点并分配到最近的质心中去
minDist = inf; minIndex = -1
for j in range(k):
distJI = distMeas(centroids[j,:],dataSet[i,:]) # 计算数据点到质心的距离
if distJI < minDist: # 如果距离比 minDist（最小距离）还小，更新 minDist（最小距离）和最小质心的 index（索引）
minDist = distJI; minIndex = j
if clusterAssment[i, 0] != minIndex: # 簇分配结果改变
clusterChanged = True # 簇改变
clusterAssment[i, :] = minIndex,minDist**2 # 更新簇分配结果为最小质心的 index（索引），minDist（最小距离）的平方
print centroids
for cent in range(k): # 更新质心
ptsInClust = dataSet[nonzero(clusterAssment[:, 0].A==cent)[0]] # 获取该簇中的所有点
centroids[cent,:] = mean(ptsInClust, axis=0) # 将质心修改为簇中所有点的平均值，mean 就是求平均值的
return centroids, clusterAssment
```
#### 测试函数
1. 测试一下以上的基础函数是否可以如预期运行, 请看: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/10.kmeans/kMeans.py>
2. 测试一下 kMeans 函数是否可以如预期运行, 请看: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/10.kmeans/kMeans.py>
参考运行结果如下:
![K-Means 运行结果1](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/apachecn-k-means-run-result-1.jpg)
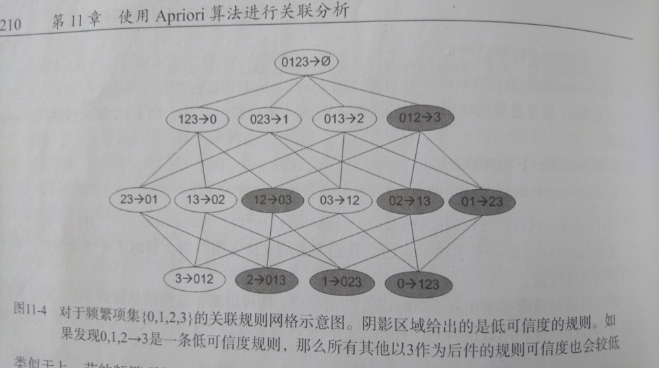
### K-Means 聚类算法的缺陷
> 在 kMeans 的函数测试中，可能偶尔会陷入局部最小值（局部最优的结果，但不是全局最优的结果）.
局部最小值的的情况如下:
![K-Means 局部最小值1](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/apachecn-kmeans-partial-best-result-1.jpg)
出现这个问题有很多原因，可能是k值取的不合适，可能是距离函数不合适，可能是最初随机选取的质心靠的太近，也可能是数据本身分布的问题。
为了解决这个问题，我们可以对生成的簇进行后处理，一种方法是将具有最大**SSE**值的簇划分成两个簇。具体实现时可以将最大簇包含的点过滤出来并在这些点上运行K-均值算法，令k设为2。
为了保持簇总数不变，可以将某两个簇进行合并。从上图中很明显就可以看出，应该将上图下部两个出错的簇质心进行合并。那么问题来了，我们可以很容易对二维数据上的聚类进行可视化， 但是如果遇到40维的数据应该如何去做？
有两种可以量化的办法: 合并最近的质心，或者合并两个使得**SSE**增幅最小的质心。 第一种思路通过计算所有质心之间的距离， 然后合并距离最近的两个点来实现。第二种方法需要合并两个簇然后计算总**SSE**值。必须在所有可能的两个簇上重复上述处理过程，直到找到合并最佳的两个簇为止。
因为上述后处理过程实在是有些繁琐，所以有更厉害的大佬提出了另一个称之为二分K-均值（bisecting K-Means）的算法.
### 二分 K-Means 聚类算法
该算法首先将所有点作为一个簇，然后将该簇一分为二。
之后选择其中一个簇继续进行划分，选择哪一个簇进行划分取决于对其划分时候可以最大程度降低 SSE（平方和误差）的值。
上述基于 SSE 的划分过程不断重复，直到得到用户指定的簇数目为止。
#### 二分 K-Means 聚类算法伪代码
* 将所有点看成一个簇
* 当簇数目小于 k 时
* 对于每一个簇
* 计算总误差
* 在给定的簇上面进行 KMeans 聚类（k=2）
* 计算将该簇一分为二之后的总误差
* 选择使得误差最小的那个簇进行划分操作
另一种做法是选择 SSE 最大的簇进行划分，直到簇数目达到用户指定的数目位置。
接下来主要介绍该做法的python2代码实现
#### 二分 K-Means 聚类算法代码
```python
# 二分 KMeans 聚类算法, 基于 kMeans 基础之上的优化，以避免陷入局部最小值
def biKMeans(dataSet, k, distMeas=distEclud):
m = shape(dataSet)[0]
clusterAssment = mat(zeros((m,2))) # 保存每个数据点的簇分配结果和平方误差
centroid0 = mean(dataSet, axis=0).tolist()[0] # 质心初始化为所有数据点的均值
centList =[centroid0] # 初始化只有 1 个质心的 list
for j in range(m): # 计算所有数据点到初始质心的距离平方误差
clusterAssment[j,1] = distMeas(mat(centroid0), dataSet[j,:])**2
while (len(centList) < k): # 当质心数量小于 k 时
lowestSSE = inf
for i in range(len(centList)): # 对每一个质心
ptsInCurrCluster = dataSet[nonzero(clusterAssment[:,0].A==i)[0],:] # 获取当前簇 i 下的所有数据点
centroidMat, splitClustAss = kMeans(ptsInCurrCluster, 2, distMeas) # 将当前簇 i 进行二分 kMeans 处理
sseSplit = sum(splitClustAss[:,1]) # 将二分 kMeans 结果中的平方和的距离进行求和
sseNotSplit = sum(clusterAssment[nonzero(clusterAssment[:,0].A!=i)[0],1]) # 将未参与二分 kMeans 分配结果中的平方和的距离进行求和
print "sseSplit, and notSplit: ",sseSplit,sseNotSplit
if (sseSplit + sseNotSplit) < lowestSSE: # 总的（未拆分和已拆分）误差和越小，越相似，效果越优化，划分的结果更好（注意: 这里的理解很重要，不明白的地方可以和我们一起讨论）
bestCentToSplit = i
bestNewCents = centroidMat
bestClustAss = splitClustAss.copy()
lowestSSE = sseSplit + sseNotSplit
# 找出最好的簇分配结果
bestClustAss[nonzero(bestClustAss[:,0].A == 1)[0],0] = len(centList) # 调用二分 kMeans 的结果，默认簇是 0,1. 当然也可以改成其它的数字
bestClustAss[nonzero(bestClustAss[:,0].A == 0)[0],0] = bestCentToSplit # 更新为最佳质心
print 'the bestCentToSplit is: ',bestCentToSplit
print 'the len of bestClustAss is: ', len(bestClustAss)
# 更新质心列表
centList[bestCentToSplit] = bestNewCents[0,:].tolist()[0] # 更新原质心 list 中的第 i 个质心为使用二分 kMeans 后 bestNewCents 的第一个质心
centList.append(bestNewCents[1,:].tolist()[0]) # 添加 bestNewCents 的第二个质心
clusterAssment[nonzero(clusterAssment[:,0].A == bestCentToSplit)[0],:]= bestClustAss # 重新分配最好簇下的数据（质心）以及SSE
return mat(centList), clusterAssment
```
#### 测试二分 KMeans 聚类算法
* 测试一下二分 KMeans 聚类算法，请看: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/10.kmeans/kMeans.py>
上述函数可以运行多次，聚类会收敛到全局最小值，而原始的 kMeans() 函数偶尔会陷入局部最小值。
运行参考结果如下:
![二分 K-Means 运行结果1](http://data.apachecn.org/img/AiLearning/ml/10.KMeans/apachecn-bikmeans-run-result-1.jpg)
* **作者: [那伊抹微笑](http://cwiki.apachecn.org/display/~xuxin), [清都江水郎](http://cwiki.apachecn.org/display/~xuzhaoqing)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**

792
docs/ml/11.使用Apriori算法进行关联分析.md → docs/ml/11.md
View File

@@ -1,396 +1,396 @@
# 第 11 章 使用 Apriori 算法进行关联分析
![](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/apachecn_apriori_homepage.jpg)
## 关联分析
关联分析是一种在大规模数据集中寻找有趣关系的任务。
这些关系可以有两种形式:
* 频繁项集（frequent item sets）: 经常出现在一块的物品的集合。
* 关联规则（associational rules）: 暗示两种物品之间可能存在很强的关系。
## 相关术语
* 关联分析（关联规则学习): 从大规模数据集中寻找物品间的隐含关系被称作 `关联分析(associati analysis)` 或者 `关联规则学习（association rule learning）` 。
下面是用一个 `杂货店` 例子来说明这两个概念，如下图所示:
![关联分析示例1](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/apachecn_apriori_association_demo_1.jpg)
* 频繁项集: {葡萄酒, 尿布, 豆奶} 就是一个频繁项集的例子。
* 关联规则: 尿布 -> 葡萄酒 就是一个关联规则。这意味着如果顾客买了尿布，那么他很可能会买葡萄酒。
那么 `频繁` 的定义是什么呢？怎么样才算频繁呢？
度量它们的方法有很多种，这里我们来简单的介绍下支持度和可信度。
* 支持度: 数据集中包含该项集的记录所占的比例。例如上图中，{豆奶} 的支持度为 4/5。{豆奶, 尿布} 的支持度为 3/5。
* 可信度: 针对一条诸如 {尿布} -> {葡萄酒} 这样具体的关联规则来定义的。这条规则的 `可信度` 被定义为 `支持度({尿布, 葡萄酒})/支持度({尿布})`，从图中可以看出 支持度({尿布, 葡萄酒}) = 3/5，支持度({尿布}) = 4/5，所以 {尿布} -> {葡萄酒} 的可信度 = 3/5 / 4/5 = 3/4 = 0.75。
`支持度` 和 `可信度` 是用来量化 `关联分析` 是否成功的一个方法。
假设想找到支持度大于 0.8 的所有项集，应该如何去做呢？
一个办法是生成一个物品所有可能组合的清单，然后对每一种组合统计它出现的频繁程度，但是当物品成千上万时，上述做法就非常非常慢了。
我们需要详细分析下这种情况并讨论下 Apriori 原理，该原理会减少关联规则学习时所需的计算量。
## Apriori 原理
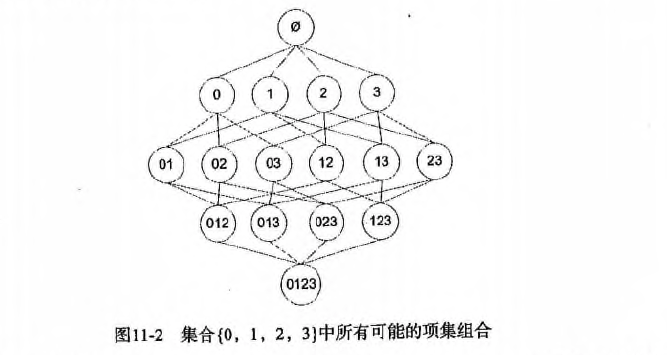
假设我们一共有 4 个商品: 商品0, 商品1, 商品2, 商品3。
所有可能的情况如下:
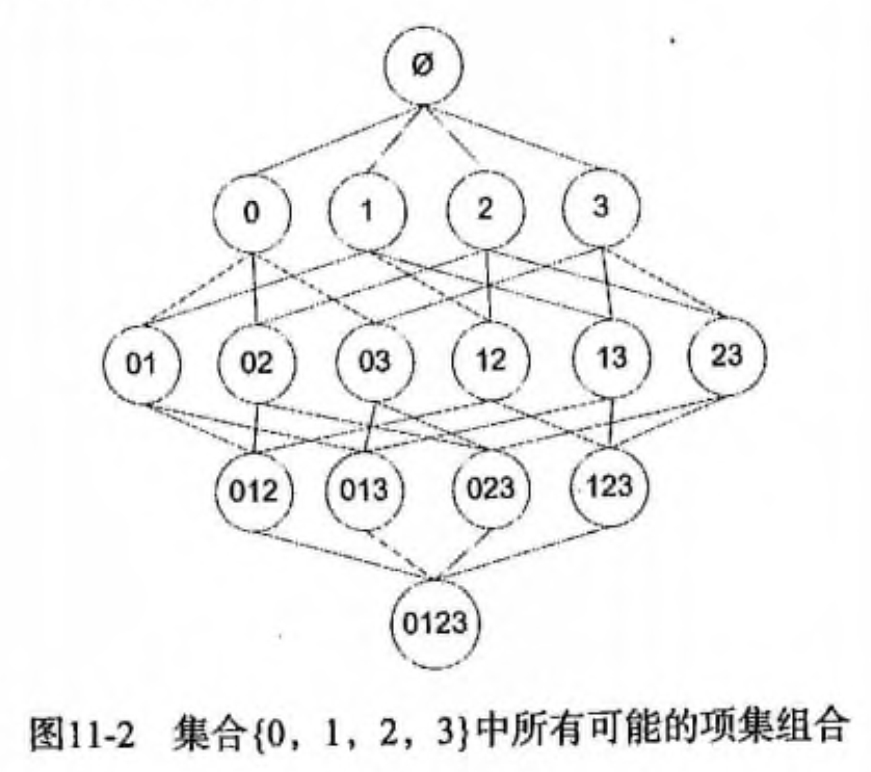
![4种商品的所有组合](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/apachecn_apriori_goods_all_1.jpg)
如果我们计算所有组合的支持度，也需要计算 15 次。即 2^N - 1 = 2^4 - 1 = 15。
随着物品的增加，计算的次数呈指数的形式增长 ...
为了降低计算次数和时间，研究人员发现了一种所谓的 Apriori 原理，即某个项集是频繁的，那么它的所有子集也是频繁的。
例如，如果 {0, 1} 是频繁的，那么 {0}, {1} 也是频繁的。
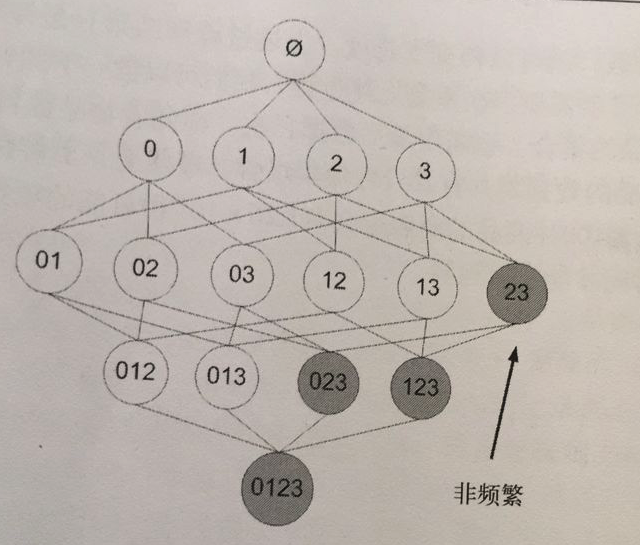
该原理直观上没有什么帮助，但是如果反过来看就有用了，也就是说如果一个项集是 `非频繁项集`，那么它的所有超集也是非频繁项集，如下图所示:
![非频繁项集](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/非频繁项集.png)
在图中我们可以看到，已知灰色部分 {2,3} 是 `非频繁项集`，那么利用上面的知识，我们就可以知道 {0,2,3} {1,2,3} {0,1,2,3} 都是 `非频繁的`。
也就是说，计算出 {2,3} 的支持度，知道它是 `非频繁` 的之后，就不需要再计算 {0,2,3} {1,2,3} {0,1,2,3} 的支持度，因为我们知道这些集合不会满足我们的要求。
使用该原理就可以避免项集数目的指数增长，从而在合理的时间内计算出频繁项集。
Apriori 算法优缺点
```
* 优点: 易编码实现
* 缺点: 在大数据集上可能较慢
* 适用数据类型: 数值型 或者 标称型数据。
```
Apriori 算法流程步骤:
```
* 收集数据: 使用任意方法。
* 准备数据: 任何数据类型都可以，因为我们只保存集合。
* 分析数据: 使用任意方法。
* 训练数据: 使用Apiori算法来找到频繁项集。
* 测试算法: 不需要测试过程。
* 使用算法: 用于发现频繁项集以及物品之间的关联规则。
```
## Apriori 算法的使用
前面提到，关联分析的目标包括两项: 发现 `频繁项集` 和发现 `关联规则`。
首先需要找到 `频繁项集`，然后才能发现 `关联规则`。
`Apriori` 算法是发现 `频繁项集` 的一种方法。
Apriori 算法的两个输入参数分别是最小支持度和数据集。
该算法首先会生成所有单个物品的项集列表。
接着扫描交易记录来查看哪些项集满足最小支持度要求，那些不满足最小支持度要求的集合会被去掉。
燃尽后对生下来的集合进行组合以声场包含两个元素的项集。
接下来再重新扫描交易记录，去掉不满足最小支持度的项集。
该过程重复进行直到所有项集被去掉。
### 生成候选项集
下面会创建一个用于构建初始集合的函数，也会创建一个通过扫描数据集以寻找交易记录子集的函数，
数据扫描的伪代码如下:
* 对数据集中的每条交易记录 tran
* 对每个候选项集 can
* 检查一下 can 是否是 tran 的子集: 如果是则增加 can 的计数值
* 对每个候选项集
* 如果其支持度不低于最小值，则保留该项集
* 返回所有频繁项集列表
以下是一些辅助函数。
#### 加载数据集
```python
# 加载数据集
def loadDataSet():
return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
```
#### 创建集合 C1。即对 dataSet 进行去重，排序，放入 list 中，然后转换所有的元素为 frozenset
```python
# 创建集合 C1。即对 dataSet 进行去重，排序，放入 list 中，然后转换所有的元素为 frozenset
def createC1(dataSet):
"""createC1（创建集合 C1）
Args:
dataSet 原始数据集
Returns:
frozenset 返回一个 frozenset 格式的 list
"""
C1 = []
for transaction in dataSet:
for item in transaction:
if not [item] in C1:
# 遍历所有的元素，如果不在 C1 出现过，那么就 append
C1.append([item])
# 对数组进行 `从小到大` 的排序
print 'sort 前=', C1
C1.sort()
# frozenset 表示冻结的 set 集合，元素无改变；可以把它当字典的 key 来使用
print 'sort 后=', C1
print 'frozenset=', map(frozenset, C1)
return map(frozenset, C1)
```
#### 计算候选数据集 CK 在数据集 D 中的支持度，并返回支持度大于最小支持度（minSupport）的数据
```python
# 计算候选数据集 CK 在数据集 D 中的支持度，并返回支持度大于最小支持度（minSupport）的数据
def scanD(D, Ck, minSupport):
"""scanD（计算候选数据集 CK 在数据集 D 中的支持度，并返回支持度大于最小支持度 minSupport 的数据）
Args:
D 数据集
Ck 候选项集列表
minSupport 最小支持度
Returns:
retList 支持度大于 minSupport 的集合
supportData 候选项集支持度数据
"""
# ssCnt 临时存放选数据集 Ck 的频率. 例如: a->10, b->5, c->8
ssCnt = {}
for tid in D:
for can in Ck:
# s.issubset(t) 测试是否 s 中的每一个元素都在 t 中
if can.issubset(tid):
if not ssCnt.has_key(can):
ssCnt[can] = 1
else:
ssCnt[can] += 1
numItems = float(len(D)) # 数据集 D 的数量
retList = []
supportData = {}
for key in ssCnt:
# 支持度 = 候选项（key）出现的次数 / 所有数据集的数量
support = ssCnt[key]/numItems
if support >= minSupport:
# 在 retList 的首位插入元素，只存储支持度满足频繁项集的值
retList.insert(0, key)
# 存储所有的候选项（key）和对应的支持度（support）
supportData[key] = support
return retList, supportData
```
完整代码地址: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/11.Apriori/apriori.py>
### 组织完整的 Apriori 算法
#### 输入频繁项集列表 Lk 与返回的元素个数 k，然后输出所有可能的候选项集 Ck
```python
# 输入频繁项集列表 Lk 与返回的元素个数 k，然后输出所有可能的候选项集 Ck
def aprioriGen(Lk, k):
"""aprioriGen（输入频繁项集列表 Lk 与返回的元素个数 k，然后输出候选项集 Ck。
例如: 以 {0},{1},{2} 为输入且 k = 2 则输出 {0,1}, {0,2}, {1,2}. 以 {0,1},{0,2},{1,2} 为输入且 k = 3 则输出 {0,1,2}
仅需要计算一次，不需要将所有的结果计算出来，然后进行去重操作
这是一个更高效的算法）
Args:
Lk 频繁项集列表
k 返回的项集元素个数（若元素的前 k-2 相同，就进行合并）
Returns:
retList 元素两两合并的数据集
"""
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i+1, lenLk):
L1 = list(Lk[i])[: k-2]
L2 = list(Lk[j])[: k-2]
# print '-----i=', i, k-2, Lk, Lk[i], list(Lk[i])[: k-2]
# print '-----j=', j, k-2, Lk, Lk[j], list(Lk[j])[: k-2]
L1.sort()
L2.sort()
# 第一次 L1,L2 为空，元素直接进行合并，返回元素两两合并的数据集
# if first k-2 elements are equal
if L1 == L2:
# set union
# print 'union=', Lk[i] | Lk[j], Lk[i], Lk[j]
retList.append(Lk[i] | Lk[j])
return retList
```
#### 找出数据集 dataSet 中支持度 >= 最小支持度的候选项集以及它们的支持度。即我们的频繁项集。
```python
# 找出数据集 dataSet 中支持度 >= 最小支持度的候选项集以及它们的支持度。即我们的频繁项集。
def apriori(dataSet, minSupport=0.5):
"""apriori（首先构建集合 C1，然后扫描数据集来判断这些只有一个元素的项集是否满足最小支持度的要求。那么满足最小支持度要求的项集构成集合 L1。然后 L1 中的元素相互组合成 C2，C2 再进一步过滤变成 L2，然后以此类推，知道 CN 的长度为 0 时结束，即可找出所有频繁项集的支持度。）
Args:
dataSet 原始数据集
minSupport 支持度的阈值
Returns:
L 频繁项集的全集
supportData 所有元素和支持度的全集
"""
# C1 即对 dataSet 进行去重，排序，放入 list 中，然后转换所有的元素为 frozenset
C1 = createC1(dataSet)
# 对每一行进行 set 转换，然后存放到集合中
D = map(set, dataSet)
print 'D=', D
# 计算候选数据集 C1 在数据集 D 中的支持度，并返回支持度大于 minSupport 的数据
L1, supportData = scanD(D, C1, minSupport)
# print "L1=", L1, "\n", "outcome: ", supportData
# L 加了一层 list, L 一共 2 层 list
L = [L1]
k = 2
# 判断 L 的第 k-2 项的数据长度是否 > 0。第一次执行时 L 为 [[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])]]。L[k-2]=L[0]=[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])]，最后面 k += 1
while (len(L[k-2]) > 0):
print 'k=', k, L, L[k-2]
Ck = aprioriGen(L[k-2], k) # 例如: 以 {0},{1},{2} 为输入且 k = 2 则输出 {0,1}, {0,2}, {1,2}. 以 {0,1},{0,2},{1,2} 为输入且 k = 3 则输出 {0,1,2}
print 'Ck', Ck
Lk, supK = scanD(D, Ck, minSupport) # 计算候选数据集 CK 在数据集 D 中的支持度，并返回支持度大于 minSupport 的数据
# 保存所有候选项集的支持度，如果字典没有，就追加元素，如果有，就更新元素
supportData.update(supK)
if len(Lk) == 0:
break
# Lk 表示满足频繁子项的集合，L 元素在增加，例如:
# l=[[set(1), set(2), set(3)]]
# l=[[set(1), set(2), set(3)], [set(1, 2), set(2, 3)]]
L.append(Lk)
k += 1
# print 'k=', k, len(L[k-2])
return L, supportData
```
到这一步，我们就找出我们所需要的 `频繁项集` 和他们的 `支持度` 了，接下来再找出关联规则即可！
完整代码地址: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/11.Apriori/apriori.py>
## 从频繁项集中挖掘关联规则
前面我们介绍了用于发现 `频繁项集` 的 Apriori 算法，现在要解决的问题是如何找出 `关联规则`。
要找到 `关联规则`，我们首先从一个 `频繁项集` 开始。
我们知道集合中的元素是不重复的，但我们想知道基于这些元素能否获得其它内容。
某个元素或某个元素集合可能会推导出另一个元素。
从先前 `杂货店` 的例子可以得到，如果有一个频繁项集 {豆奶,莴苣}，那么就可能有一条关联规则 “豆奶 -> 莴苣”。
这意味着如果有人买了豆奶，那么在统计上他会购买莴苣的概率比较大。
但是，这一条件反过来并不总是成立。
也就是说 “豆奶 -> 莴苣” 统计上显著，那么 “莴苣 -> 豆奶” 也不一定成立。
前面我们给出了 `频繁项集` 的量化定义，即它满足最小支持度要求。
对于 `关联规则`，我们也有类似的量化方法，这种量化指标称之为 `可信度`。
一条规则 A -> B 的可信度定义为 support(A | B) / support(A)。（注意: 在 python 中 | 表示集合的并操作，而数学书集合并的符号是 U）。
`A | B` 是指所有出现在集合 A 或者集合 B 中的元素。
由于我们先前已经计算出所有 `频繁项集` 的支持度了，现在我们要做的只不过是提取这些数据做一次除法运算即可。
### 一个频繁项集可以产生多少条关联规则呢？
如下图所示，给出的是项集 {0,1,2,3} 产生的所有关联规则:
![关联规则网格示意图](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/apachecn_association_rule_demo_1.jpg)
与我们前面的 `频繁项集` 生成一样，我们可以为每个频繁项集产生许多关联规则。
如果能减少规则的数目来确保问题的可解析，那么计算起来就会好很多。
通过观察，我们可以知道，如果某条规则并不满足 `最小可信度` 要求，那么该规则的所有子集也不会满足 `最小可信度` 的要求。
如上图所示，假设 `123 -> 3` 并不满足最小可信度要求，那么就知道任何左部为 {0,1,2} 子集的规则也不会满足 `最小可信度` 的要求。
即 `12 -> 03` , `02 -> 13` , `01 -> 23` , `2 -> 013`, ` 1 -> 023`, `0 -> 123` 都不满足 `最小可信度` 要求。
可以利用关联规则的上述性质属性来减少需要测试的规则数目，跟先前 Apriori 算法的套路一样。
以下是一些辅助函数:
#### 计算可信度
```python
# 计算可信度（confidence）
def calcConf(freqSet, H
, supportData, brl, minConf=0.7):
"""calcConf（对两个元素的频繁项，计算可信度，例如: {1,2}/{1} 或者 {1,2}/{2} 看是否满足条件）
Args:
freqSet 频繁项集中的元素，例如: frozenset([1, 3])
H 频繁项集中的元素的集合，例如: [frozenset([1]), frozenset([3])]
supportData 所有元素的支持度的字典
brl 关联规则列表的空数组
minConf 最小可信度
Returns:
prunedH 记录 可信度大于阈值的集合
"""
# 记录可信度大于最小可信度（minConf）的集合
prunedH = []
for conseq in H: # 假设 freqSet = frozenset([1, 3]), H = [frozenset([1]), frozenset([3])]，那么现在需要求出 frozenset([1]) -> frozenset([3]) 的可信度和 frozenset([3]) -> frozenset([1]) 的可信度
# print 'confData=', freqSet, H, conseq, freqSet-conseq
conf = supportData[freqSet]/supportData[freqSet-conseq] # 支持度定义: a -> b = support(a | b) / support(a). 假设 freqSet = frozenset([1, 3]), conseq = [frozenset([1])]，那么 frozenset([1]) 至 frozenset([3]) 的可信度为 = support(a | b) / support(a) = supportData[freqSet]/supportData[freqSet-conseq] = supportData[frozenset([1, 3])] / supportData[frozenset([1])]
if conf >= minConf:
# 只要买了 freqSet-conseq 集合，一定会买 conseq 集合（freqSet-conseq 集合和 conseq 集合是全集）
print freqSet-conseq, '-->', conseq, 'conf:', conf
brl.append((freqSet-conseq, conseq, conf))
prunedH.append(conseq)
return prunedH
````
#### 递归计算频繁项集的规则
```python
# 递归计算频繁项集的规则
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
"""rulesFromConseq
Args:
freqSet 频繁项集中的元素，例如: frozenset([2, 3, 5])
H 频繁项集中的元素的集合，例如: [frozenset([2]), frozenset([3]), frozenset([5])]
supportData 所有元素的支持度的字典
brl 关联规则列表的数组
minConf 最小可信度
"""
# H[0] 是 freqSet 的元素组合的第一个元素，并且 H 中所有元素的长度都一样，长度由 aprioriGen(H, m+1) 这里的 m + 1 来控制
# 该函数递归时，H[0] 的长度从 1 开始增长 1 2 3 ...
# 假设 freqSet = frozenset([2, 3, 5]), H = [frozenset([2]), frozenset([3]), frozenset([5])]
# 那么 m = len(H[0]) 的递归的值依次为 1 2
# 在 m = 2 时, 跳出该递归。假设再递归一次，那么 H[0] = frozenset([2, 3, 5])，freqSet = frozenset([2, 3, 5]) ，没必要再计算 freqSet 与 H[0] 的关联规则了。
m = len(H[0])
if (len(freqSet) > (m + 1)):
print 'freqSet******************', len(freqSet), m + 1, freqSet, H, H[0]
# 生成 m+1 个长度的所有可能的 H 中的组合，假设 H = [frozenset([2]), frozenset([3]), frozenset([5])]
# 第一次递归调用时生成 [frozenset([2, 3]), frozenset([2, 5]), frozenset([3, 5])]
# 第二次 。。。没有第二次，递归条件判断时已经退出了
Hmp1 = aprioriGen(H, m+1)
# 返回可信度大于最小可信度的集合
Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
print 'Hmp1=', Hmp1
print 'len(Hmp1)=', len(Hmp1), 'len(freqSet)=', len(freqSet)
# 计算可信度后，还有数据大于最小可信度的话，那么继续递归调用，否则跳出递归
if (len(Hmp1) > 1):
print '----------------------', Hmp1
# print len(freqSet), len(Hmp1[0]) + 1
rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)
```
#### 生成关联规则
```python
# 生成关联规则
def generateRules(L, supportData, minConf=0.7):
"""generateRules
Args:
L 频繁项集列表
supportData 频繁项集支持度的字典
minConf 最小置信度
Returns:
bigRuleList 可信度规则列表（关于 (A->B+置信度) 3个字段的组合）
"""
bigRuleList = []
# 假设 L = [[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])], [frozenset([1, 3]), frozenset([2, 5]), frozenset([2, 3]), frozenset([3, 5])], [frozenset([2, 3, 5])]]
for i in range(1, len(L)):
# 获取频繁项集中每个组合的所有元素
for freqSet in L[i]:
# 假设: freqSet= frozenset([1, 3]), H1=[frozenset([1]), frozenset([3])]
# 组合总的元素并遍历子元素，并转化为 frozenset 集合，再存放到 list 列表中
H1 = [frozenset([item]) for item in freqSet]
# 2 个的组合，走 else, 2 个以上的组合，走 if
if (i > 1):
rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
else:
calcConf(freqSet, H1, supportData, bigRuleList, minConf)
return bigRuleList
```
到这里为止，通过调用 generateRules 函数即可得出我们所需的 `关联规则`。
* 分级法: 频繁项集->关联规则
* 1.首先从一个频繁项集开始，接着创建一个规则列表，其中规则右部分只包含一个元素，然后对这个规则进行测试。
* 2.接下来合并所有剩余规则来创建一个新的规则列表，其中规则右部包含两个元素。
* 如下图:
* ![所有可能的项集组合](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/所有可能的项集组合.png)
* 最后: 每次增加频繁项集的大小，Apriori 算法都会重新扫描整个数据集，是否有优化空间呢？ 下一章: FP-growth算法等着你的到来
* * *
* **作者: [片刻](https://github.com/jiangzhonglian)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**
# 第 11 章 使用 Apriori 算法进行关联分析
![](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/apachecn_apriori_homepage.jpg)
## 关联分析
关联分析是一种在大规模数据集中寻找有趣关系的任务。
这些关系可以有两种形式:
* 频繁项集（frequent item sets）: 经常出现在一块的物品的集合。
* 关联规则（associational rules）: 暗示两种物品之间可能存在很强的关系。
## 相关术语
* 关联分析（关联规则学习): 从大规模数据集中寻找物品间的隐含关系被称作 `关联分析(associati analysis)` 或者 `关联规则学习（association rule learning）` 。
下面是用一个 `杂货店` 例子来说明这两个概念，如下图所示:
![关联分析示例1](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/apachecn_apriori_association_demo_1.jpg)
* 频繁项集: {葡萄酒, 尿布, 豆奶} 就是一个频繁项集的例子。
* 关联规则: 尿布 -> 葡萄酒 就是一个关联规则。这意味着如果顾客买了尿布，那么他很可能会买葡萄酒。
那么 `频繁` 的定义是什么呢？怎么样才算频繁呢？
度量它们的方法有很多种，这里我们来简单的介绍下支持度和可信度。
* 支持度: 数据集中包含该项集的记录所占的比例。例如上图中，{豆奶} 的支持度为 4/5。{豆奶, 尿布} 的支持度为 3/5。
* 可信度: 针对一条诸如 {尿布} -> {葡萄酒} 这样具体的关联规则来定义的。这条规则的 `可信度` 被定义为 `支持度({尿布, 葡萄酒})/支持度({尿布})`，从图中可以看出 支持度({尿布, 葡萄酒}) = 3/5，支持度({尿布}) = 4/5，所以 {尿布} -> {葡萄酒} 的可信度 = 3/5 / 4/5 = 3/4 = 0.75。
`支持度` 和 `可信度` 是用来量化 `关联分析` 是否成功的一个方法。
假设想找到支持度大于 0.8 的所有项集，应该如何去做呢？
一个办法是生成一个物品所有可能组合的清单，然后对每一种组合统计它出现的频繁程度，但是当物品成千上万时，上述做法就非常非常慢了。
我们需要详细分析下这种情况并讨论下 Apriori 原理，该原理会减少关联规则学习时所需的计算量。
## Apriori 原理
假设我们一共有 4 个商品: 商品0, 商品1, 商品2, 商品3。
所有可能的情况如下:
![4种商品的所有组合](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/apachecn_apriori_goods_all_1.jpg)
如果我们计算所有组合的支持度，也需要计算 15 次。即 2^N - 1 = 2^4 - 1 = 15。
随着物品的增加，计算的次数呈指数的形式增长 ...
为了降低计算次数和时间，研究人员发现了一种所谓的 Apriori 原理，即某个项集是频繁的，那么它的所有子集也是频繁的。
例如，如果 {0, 1} 是频繁的，那么 {0}, {1} 也是频繁的。
该原理直观上没有什么帮助，但是如果反过来看就有用了，也就是说如果一个项集是 `非频繁项集`，那么它的所有超集也是非频繁项集，如下图所示:
![非频繁项集](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/非频繁项集.png)
在图中我们可以看到，已知灰色部分 {2,3} 是 `非频繁项集`，那么利用上面的知识，我们就可以知道 {0,2,3} {1,2,3} {0,1,2,3} 都是 `非频繁的`。
也就是说，计算出 {2,3} 的支持度，知道它是 `非频繁` 的之后，就不需要再计算 {0,2,3} {1,2,3} {0,1,2,3} 的支持度，因为我们知道这些集合不会满足我们的要求。
使用该原理就可以避免项集数目的指数增长，从而在合理的时间内计算出频繁项集。
Apriori 算法优缺点
```
* 优点: 易编码实现
* 缺点: 在大数据集上可能较慢
* 适用数据类型: 数值型 或者 标称型数据。
```
Apriori 算法流程步骤:
```
* 收集数据: 使用任意方法。
* 准备数据: 任何数据类型都可以，因为我们只保存集合。
* 分析数据: 使用任意方法。
* 训练数据: 使用Apiori算法来找到频繁项集。
* 测试算法: 不需要测试过程。
* 使用算法: 用于发现频繁项集以及物品之间的关联规则。
```
## Apriori 算法的使用
前面提到，关联分析的目标包括两项: 发现 `频繁项集` 和发现 `关联规则`。
首先需要找到 `频繁项集`，然后才能发现 `关联规则`。
`Apriori` 算法是发现 `频繁项集` 的一种方法。
Apriori 算法的两个输入参数分别是最小支持度和数据集。
该算法首先会生成所有单个物品的项集列表。
接着扫描交易记录来查看哪些项集满足最小支持度要求，那些不满足最小支持度要求的集合会被去掉。
燃尽后对生下来的集合进行组合以声场包含两个元素的项集。
接下来再重新扫描交易记录，去掉不满足最小支持度的项集。
该过程重复进行直到所有项集被去掉。
### 生成候选项集
下面会创建一个用于构建初始集合的函数，也会创建一个通过扫描数据集以寻找交易记录子集的函数，
数据扫描的伪代码如下:
* 对数据集中的每条交易记录 tran
* 对每个候选项集 can
* 检查一下 can 是否是 tran 的子集: 如果是则增加 can 的计数值
* 对每个候选项集
* 如果其支持度不低于最小值，则保留该项集
* 返回所有频繁项集列表
以下是一些辅助函数。
#### 加载数据集
```python
# 加载数据集
def loadDataSet():
return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
```
#### 创建集合 C1。即对 dataSet 进行去重，排序，放入 list 中，然后转换所有的元素为 frozenset
```python
# 创建集合 C1。即对 dataSet 进行去重，排序，放入 list 中，然后转换所有的元素为 frozenset
def createC1(dataSet):
"""createC1（创建集合 C1）
Args:
dataSet 原始数据集
Returns:
frozenset 返回一个 frozenset 格式的 list
"""
C1 = []
for transaction in dataSet:
for item in transaction:
if not [item] in C1:
# 遍历所有的元素，如果不在 C1 出现过，那么就 append
C1.append([item])
# 对数组进行 `从小到大` 的排序
print 'sort 前=', C1
C1.sort()
# frozenset 表示冻结的 set 集合，元素无改变；可以把它当字典的 key 来使用
print 'sort 后=', C1
print 'frozenset=', map(frozenset, C1)
return map(frozenset, C1)
```
#### 计算候选数据集 CK 在数据集 D 中的支持度，并返回支持度大于最小支持度（minSupport）的数据
```python
# 计算候选数据集 CK 在数据集 D 中的支持度，并返回支持度大于最小支持度（minSupport）的数据
def scanD(D, Ck, minSupport):
"""scanD（计算候选数据集 CK 在数据集 D 中的支持度，并返回支持度大于最小支持度 minSupport 的数据）
Args:
D 数据集
Ck 候选项集列表
minSupport 最小支持度
Returns:
retList 支持度大于 minSupport 的集合
supportData 候选项集支持度数据
"""
# ssCnt 临时存放选数据集 Ck 的频率. 例如: a->10, b->5, c->8
ssCnt = {}
for tid in D:
for can in Ck:
# s.issubset(t) 测试是否 s 中的每一个元素都在 t 中
if can.issubset(tid):
if not ssCnt.has_key(can):
ssCnt[can] = 1
else:
ssCnt[can] += 1
numItems = float(len(D)) # 数据集 D 的数量
retList = []
supportData = {}
for key in ssCnt:
# 支持度 = 候选项（key）出现的次数 / 所有数据集的数量
support = ssCnt[key]/numItems
if support >= minSupport:
# 在 retList 的首位插入元素，只存储支持度满足频繁项集的值
retList.insert(0, key)
# 存储所有的候选项（key）和对应的支持度（support）
supportData[key] = support
return retList, supportData
```
完整代码地址: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/11.Apriori/apriori.py>
### 组织完整的 Apriori 算法
#### 输入频繁项集列表 Lk 与返回的元素个数 k，然后输出所有可能的候选项集 Ck
```python
# 输入频繁项集列表 Lk 与返回的元素个数 k，然后输出所有可能的候选项集 Ck
def aprioriGen(Lk, k):
"""aprioriGen（输入频繁项集列表 Lk 与返回的元素个数 k，然后输出候选项集 Ck。
例如: 以 {0},{1},{2} 为输入且 k = 2 则输出 {0,1}, {0,2}, {1,2}. 以 {0,1},{0,2},{1,2} 为输入且 k = 3 则输出 {0,1,2}
仅需要计算一次，不需要将所有的结果计算出来，然后进行去重操作
这是一个更高效的算法）
Args:
Lk 频繁项集列表
k 返回的项集元素个数（若元素的前 k-2 相同，就进行合并）
Returns:
retList 元素两两合并的数据集
"""
retList = []
lenLk = len(Lk)
for i in range(lenLk):
for j in range(i+1, lenLk):
L1 = list(Lk[i])[: k-2]
L2 = list(Lk[j])[: k-2]
# print '-----i=', i, k-2, Lk, Lk[i], list(Lk[i])[: k-2]
# print '-----j=', j, k-2, Lk, Lk[j], list(Lk[j])[: k-2]
L1.sort()
L2.sort()
# 第一次 L1,L2 为空，元素直接进行合并，返回元素两两合并的数据集
# if first k-2 elements are equal
if L1 == L2:
# set union
# print 'union=', Lk[i] | Lk[j], Lk[i], Lk[j]
retList.append(Lk[i] | Lk[j])
return retList
```
#### 找出数据集 dataSet 中支持度 >= 最小支持度的候选项集以及它们的支持度。即我们的频繁项集。
```python
# 找出数据集 dataSet 中支持度 >= 最小支持度的候选项集以及它们的支持度。即我们的频繁项集。
def apriori(dataSet, minSupport=0.5):
"""apriori（首先构建集合 C1，然后扫描数据集来判断这些只有一个元素的项集是否满足最小支持度的要求。那么满足最小支持度要求的项集构成集合 L1。然后 L1 中的元素相互组合成 C2，C2 再进一步过滤变成 L2，然后以此类推，知道 CN 的长度为 0 时结束，即可找出所有频繁项集的支持度。）
Args:
dataSet 原始数据集
minSupport 支持度的阈值
Returns:
L 频繁项集的全集
supportData 所有元素和支持度的全集
"""
# C1 即对 dataSet 进行去重，排序，放入 list 中，然后转换所有的元素为 frozenset
C1 = createC1(dataSet)
# 对每一行进行 set 转换，然后存放到集合中
D = map(set, dataSet)
print 'D=', D
# 计算候选数据集 C1 在数据集 D 中的支持度，并返回支持度大于 minSupport 的数据
L1, supportData = scanD(D, C1, minSupport)
# print "L1=", L1, "\n", "outcome: ", supportData
# L 加了一层 list, L 一共 2 层 list
L = [L1]
k = 2
# 判断 L 的第 k-2 项的数据长度是否 > 0。第一次执行时 L 为 [[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])]]。L[k-2]=L[0]=[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])]，最后面 k += 1
while (len(L[k-2]) > 0):
print 'k=', k, L, L[k-2]
Ck = aprioriGen(L[k-2], k) # 例如: 以 {0},{1},{2} 为输入且 k = 2 则输出 {0,1}, {0,2}, {1,2}. 以 {0,1},{0,2},{1,2} 为输入且 k = 3 则输出 {0,1,2}
print 'Ck', Ck
Lk, supK = scanD(D, Ck, minSupport) # 计算候选数据集 CK 在数据集 D 中的支持度，并返回支持度大于 minSupport 的数据
# 保存所有候选项集的支持度，如果字典没有，就追加元素，如果有，就更新元素
supportData.update(supK)
if len(Lk) == 0:
break
# Lk 表示满足频繁子项的集合，L 元素在增加，例如:
# l=[[set(1), set(2), set(3)]]
# l=[[set(1), set(2), set(3)], [set(1, 2), set(2, 3)]]
L.append(Lk)
k += 1
# print 'k=', k, len(L[k-2])
return L, supportData
```
到这一步，我们就找出我们所需要的 `频繁项集` 和他们的 `支持度` 了，接下来再找出关联规则即可！
完整代码地址: <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/11.Apriori/apriori.py>
## 从频繁项集中挖掘关联规则
前面我们介绍了用于发现 `频繁项集` 的 Apriori 算法，现在要解决的问题是如何找出 `关联规则`。
要找到 `关联规则`，我们首先从一个 `频繁项集` 开始。
我们知道集合中的元素是不重复的，但我们想知道基于这些元素能否获得其它内容。
某个元素或某个元素集合可能会推导出另一个元素。
从先前 `杂货店` 的例子可以得到，如果有一个频繁项集 {豆奶,莴苣}，那么就可能有一条关联规则 “豆奶 -> 莴苣”。
这意味着如果有人买了豆奶，那么在统计上他会购买莴苣的概率比较大。
但是，这一条件反过来并不总是成立。
也就是说 “豆奶 -> 莴苣” 统计上显著，那么 “莴苣 -> 豆奶” 也不一定成立。
前面我们给出了 `频繁项集` 的量化定义，即它满足最小支持度要求。
对于 `关联规则`，我们也有类似的量化方法，这种量化指标称之为 `可信度`。
一条规则 A -> B 的可信度定义为 support(A | B) / support(A)。（注意: 在 python 中 | 表示集合的并操作，而数学书集合并的符号是 U）。
`A | B` 是指所有出现在集合 A 或者集合 B 中的元素。
由于我们先前已经计算出所有 `频繁项集` 的支持度了，现在我们要做的只不过是提取这些数据做一次除法运算即可。
### 一个频繁项集可以产生多少条关联规则呢？
如下图所示，给出的是项集 {0,1,2,3} 产生的所有关联规则:
![关联规则网格示意图](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/apachecn_association_rule_demo_1.jpg)
与我们前面的 `频繁项集` 生成一样，我们可以为每个频繁项集产生许多关联规则。
如果能减少规则的数目来确保问题的可解析，那么计算起来就会好很多。
通过观察，我们可以知道，如果某条规则并不满足 `最小可信度` 要求，那么该规则的所有子集也不会满足 `最小可信度` 的要求。
如上图所示，假设 `123 -> 3` 并不满足最小可信度要求，那么就知道任何左部为 {0,1,2} 子集的规则也不会满足 `最小可信度` 的要求。
即 `12 -> 03` , `02 -> 13` , `01 -> 23` , `2 -> 013`, ` 1 -> 023`, `0 -> 123` 都不满足 `最小可信度` 要求。
可以利用关联规则的上述性质属性来减少需要测试的规则数目，跟先前 Apriori 算法的套路一样。
以下是一些辅助函数:
#### 计算可信度
```python
# 计算可信度（confidence）
def calcConf(freqSet, H
, supportData, brl, minConf=0.7):
"""calcConf（对两个元素的频繁项，计算可信度，例如: {1,2}/{1} 或者 {1,2}/{2} 看是否满足条件）
Args:
freqSet 频繁项集中的元素，例如: frozenset([1, 3])
H 频繁项集中的元素的集合，例如: [frozenset([1]), frozenset([3])]
supportData 所有元素的支持度的字典
brl 关联规则列表的空数组
minConf 最小可信度
Returns:
prunedH 记录 可信度大于阈值的集合
"""
# 记录可信度大于最小可信度（minConf）的集合
prunedH = []
for conseq in H: # 假设 freqSet = frozenset([1, 3]), H = [frozenset([1]), frozenset([3])]，那么现在需要求出 frozenset([1]) -> frozenset([3]) 的可信度和 frozenset([3]) -> frozenset([1]) 的可信度
# print 'confData=', freqSet, H, conseq, freqSet-conseq
conf = supportData[freqSet]/supportData[freqSet-conseq] # 支持度定义: a -> b = support(a | b) / support(a). 假设 freqSet = frozenset([1, 3]), conseq = [frozenset([1])]，那么 frozenset([1]) 至 frozenset([3]) 的可信度为 = support(a | b) / support(a) = supportData[freqSet]/supportData[freqSet-conseq] = supportData[frozenset([1, 3])] / supportData[frozenset([1])]
if conf >= minConf:
# 只要买了 freqSet-conseq 集合，一定会买 conseq 集合（freqSet-conseq 集合和 conseq 集合是全集）
print freqSet-conseq, '-->', conseq, 'conf:', conf
brl.append((freqSet-conseq, conseq, conf))
prunedH.append(conseq)
return prunedH
````
#### 递归计算频繁项集的规则
```python
# 递归计算频繁项集的规则
def rulesFromConseq(freqSet, H, supportData, brl, minConf=0.7):
"""rulesFromConseq
Args:
freqSet 频繁项集中的元素，例如: frozenset([2, 3, 5])
H 频繁项集中的元素的集合，例如: [frozenset([2]), frozenset([3]), frozenset([5])]
supportData 所有元素的支持度的字典
brl 关联规则列表的数组
minConf 最小可信度
"""
# H[0] 是 freqSet 的元素组合的第一个元素，并且 H 中所有元素的长度都一样，长度由 aprioriGen(H, m+1) 这里的 m + 1 来控制
# 该函数递归时，H[0] 的长度从 1 开始增长 1 2 3 ...
# 假设 freqSet = frozenset([2, 3, 5]), H = [frozenset([2]), frozenset([3]), frozenset([5])]
# 那么 m = len(H[0]) 的递归的值依次为 1 2
# 在 m = 2 时, 跳出该递归。假设再递归一次，那么 H[0] = frozenset([2, 3, 5])，freqSet = frozenset([2, 3, 5]) ，没必要再计算 freqSet 与 H[0] 的关联规则了。
m = len(H[0])
if (len(freqSet) > (m + 1)):
print 'freqSet******************', len(freqSet), m + 1, freqSet, H, H[0]
# 生成 m+1 个长度的所有可能的 H 中的组合，假设 H = [frozenset([2]), frozenset([3]), frozenset([5])]
# 第一次递归调用时生成 [frozenset([2, 3]), frozenset([2, 5]), frozenset([3, 5])]
# 第二次 。。。没有第二次，递归条件判断时已经退出了
Hmp1 = aprioriGen(H, m+1)
# 返回可信度大于最小可信度的集合
Hmp1 = calcConf(freqSet, Hmp1, supportData, brl, minConf)
print 'Hmp1=', Hmp1
print 'len(Hmp1)=', len(Hmp1), 'len(freqSet)=', len(freqSet)
# 计算可信度后，还有数据大于最小可信度的话，那么继续递归调用，否则跳出递归
if (len(Hmp1) > 1):
print '----------------------', Hmp1
# print len(freqSet), len(Hmp1[0]) + 1
rulesFromConseq(freqSet, Hmp1, supportData, brl, minConf)
```
#### 生成关联规则
```python
# 生成关联规则
def generateRules(L, supportData, minConf=0.7):
"""generateRules
Args:
L 频繁项集列表
supportData 频繁项集支持度的字典
minConf 最小置信度
Returns:
bigRuleList 可信度规则列表（关于 (A->B+置信度) 3个字段的组合）
"""
bigRuleList = []
# 假设 L = [[frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])], [frozenset([1, 3]), frozenset([2, 5]), frozenset([2, 3]), frozenset([3, 5])], [frozenset([2, 3, 5])]]
for i in range(1, len(L)):
# 获取频繁项集中每个组合的所有元素
for freqSet in L[i]:
# 假设: freqSet= frozenset([1, 3]), H1=[frozenset([1]), frozenset([3])]
# 组合总的元素并遍历子元素，并转化为 frozenset 集合，再存放到 list 列表中
H1 = [frozenset([item]) for item in freqSet]
# 2 个的组合，走 else, 2 个以上的组合，走 if
if (i > 1):
rulesFromConseq(freqSet, H1, supportData, bigRuleList, minConf)
else:
calcConf(freqSet, H1, supportData, bigRuleList, minConf)
return bigRuleList
```
到这里为止，通过调用 generateRules 函数即可得出我们所需的 `关联规则`。
* 分级法: 频繁项集->关联规则
* 1.首先从一个频繁项集开始，接着创建一个规则列表，其中规则右部分只包含一个元素，然后对这个规则进行测试。
* 2.接下来合并所有剩余规则来创建一个新的规则列表，其中规则右部包含两个元素。
* 如下图:
* ![所有可能的项集组合](http://data.apachecn.org/img/AiLearning/ml/11.Apriori/所有可能的项集组合.png)
* 最后: 每次增加频繁项集的大小，Apriori 算法都会重新扫描整个数据集，是否有优化空间呢？ 下一章: FP-growth算法等着你的到来
* * *
* **作者: [片刻](https://github.com/jiangzhonglian)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**

0
docs/ml/12.使用FP-growth算法来高效发现频繁项集.md → docs/ml/12.md
View File

452
docs/ml/13.利用PCA来简化数据.md → docs/ml/13.md
View File

@@ -1,226 +1,226 @@
# 第13章 利用 PCA 来简化数据
![利用PCA简化数据_首页](http://data.apachecn.org/img/AiLearning/ml/13.PCA/利用PCA简化数据_首页.jpg)
## 降维技术
> 场景
* 我们正通过电视观看体育比赛，在电视的显示器上有一个球。
* 显示器大概包含了100万像素点，而球则可能是由较少的像素点组成，例如说一千个像素点。
* 人们实时的将显示器上的百万像素转换成为一个三维图像，该图像就给出运动场上球的位置。
* 在这个过程中，人们已经将百万像素点的数据，降至为三维。这个过程就称为`降维(dimensionality reduction)`
> 数据显示 并非大规模特征下的唯一难题，对数据进行简化还有如下一系列的原因:
* 1) 使得数据集更容易使用
* 2) 降低很多算法的计算开销
* 3) 去除噪音
* 4) 使得结果易懂
> 适用范围:
* 在已标注与未标注的数据上都有降维技术。
* 这里我们将主要关注未标注数据上的降维技术，将技术同样也可以应用于已标注的数据。
> 在以下3种降维技术中， PCA的应用目前最为广泛，因此本章主要关注PCA。
* 1) 主成分分析(Principal Component Analysis, PCA)
* `通俗理解: 就是找出一个最主要的特征，然后进行分析。`
* `例如: 考察一个人的智力情况，就直接看数学成绩就行(存在: 数学、语文、英语成绩)`
* 2) 因子分析(Factor Analysis)
* `通俗理解: 将多个实测变量转换为少数几个综合指标。它反映一种降维的思想，通过降维将相关性高的变量聚在一起,从而减少需要分析的变量的数量,而减少问题分析的复杂性`
* `例如: 考察一个人的整体情况，就直接组合3样成绩(隐变量)，看平均成绩就行(存在: 数学、语文、英语成绩)`
* 应用的领域: 社会科学、金融和其他领域
* 在因子分析中，我们
* 假设观察数据的成分中有一些观察不到的隐变量(latent variable)。
* 假设观察数据是这些隐变量和某些噪音的线性组合。
* 那么隐变量的数据可能比观察数据的数目少，也就说通过找到隐变量就可以实现数据的降维。
* 3) 独立成分分析(Independ Component Analysis, ICA)
* `通俗理解: ICA 认为观测信号是若干个独立信号的线性组合，ICA 要做的是一个解混过程。`
* `例如: 我们去ktv唱歌，想辨别唱的是什么歌曲？ICA 是观察发现是原唱唱的一首歌【2个独立的声音（原唱／主唱）】。`
* ICA 是假设数据是从 N 个数据源混合组成的，这一点和因子分析有些类似，这些数据源之间在统计上是相互独立的，而在 PCA 中只假设数据是不 相关（线性关系）的。
* 同因子分析一样，如果数据源的数目少于观察数据的数目，则可以实现降维过程。
## PCA
### PCA 概述
主成分分析(Principal Component Analysis, PCA): `通俗理解: 就是找出一个最主要的特征，然后进行分析。`
### PCA 场景
`例如: 考察一个人的智力情况，就直接看数学成绩就行(存在: 数学、语文、英语成绩)`
### PCA 原理
> PCA 工作原理
1. 找出第一个主成分的方向，也就是数据 `方差最大` 的方向。
2. 找出第二个主成分的方向，也就是数据 `方差次大` 的方向，并且该方向与第一个主成分方向 `正交(orthogonal 如果是二维空间就叫垂直)`。
3. 通过这种方式计算出所有的主成分方向。
4. 通过数据集的协方差矩阵及其特征值分析，我们就可以得到这些主成分的值。
5. 一旦得到了协方差矩阵的特征值和特征向量，我们就可以保留最大的 N 个特征。这些特征向量也给出了 N 个最重要特征的真实结构，我们就可以通过将数据乘上这 N 个特征向量 从而将它转换到新的空间上。
为什么正交？
1. 正交是为了数据有效性损失最小
2. 正交的一个原因是特征值的特征向量是正交的
例如下图:
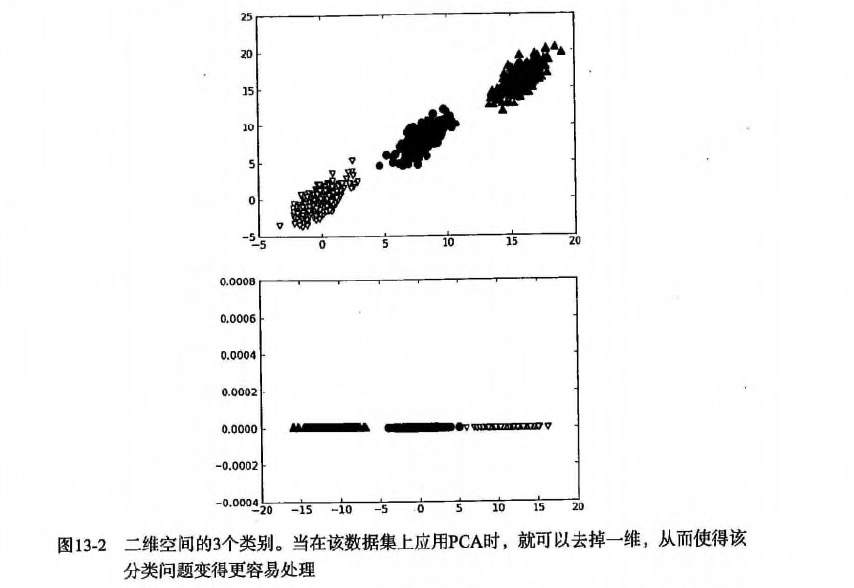
![应用PCA降维](http://data.apachecn.org/img/AiLearning/ml/13.PCA/应用PCA降维.png)
> PCA 优缺点
```
优点: 降低数据的复杂性，识别最重要的多个特征。
缺点: 不一定需要，且可能损失有用信息。
适用数据类型: 数值型数据。
```
### 项目案例: 对半导体数据进行降维处理
#### 项目概述
```
半导体是在一些极为先进的工厂中制造出来的。设备的生命早期有限，并且花费极其巨大。
虽然通过早期测试和频繁测试来发现有瑕疵的产品，但仍有一些存在瑕疵的产品通过测试。
如果我们通过机器学习技术用于发现瑕疵产品，那么它就会为制造商节省大量的资金。
具体来讲，它拥有590个特征。我们看看能否对这些特征进行降维处理。
对于数据的缺失值的问题，我们有一些处理方法(参考第5章)
目前该章节处理的方案是: 将缺失值NaN(Not a Number缩写)，全部用平均值来替代(如果用0来处理的策略就太差劲了)。
```
#### 开发流程
> 收集数据: 提供文本文件
文件名: secom.data
文本文件数据格式如下:
```
3030.93 2564 2187.7333 1411.1265 1.3602 100 97.6133 0.1242 1.5005 0.0162 -0.0034 0.9455 202.4396 0 7.9558 414.871 10.0433 0.968 192.3963 12.519 1.4026 -5419 2916.5 -4043.75 751 0.8955 1.773 3.049 64.2333 2.0222 0.1632 3.5191 83.3971 9.5126 50.617 64.2588 49.383 66.3141 86.9555 117.5132 61.29 4.515 70 352.7173 10.1841 130.3691 723.3092 1.3072 141.2282 1 624.3145 218.3174 0 4.592 4.841 2834 0.9317 0.9484 4.7057 -1.7264 350.9264 10.6231 108.6427 16.1445 21.7264 29.5367 693.7724 0.9226 148.6009 1 608.17 84.0793 NaN NaN 0 0.0126 -0.0206 0.0141 -0.0307 -0.0083 -0.0026 -0.0567 -0.0044 7.2163 0.132 NaN 2.3895 0.969 1747.6049 0.1841 8671.9301 -0.3274 -0.0055 -0.0001 0.0001 0.0003 -0.2786 0 0.3974 -0.0251 0.0002 0.0002 0.135 -0.0042 0.0003 0.0056 0 -0.2468 0.3196 NaN NaN NaN NaN 0.946 0 748.6115 0.9908 58.4306 0.6002 0.9804 6.3788 15.88 2.639 15.94 15.93 0.8656 3.353 0.4098 3.188 -0.0473 0.7243 0.996 2.2967 1000.7263 39.2373 123 111.3 75.2 46.2 350.671 0.3948 0 6.78 0.0034 0.0898 0.085 0.0358 0.0328 12.2566 0 4.271 10.284 0.4734 0.0167 11.8901 0.41 0.0506 NaN NaN 1017 967 1066 368 0.09 0.048 0.095 2 0.9 0.069 0.046 0.725 0.1139 0.3183 0.5888 0.3184 0.9499 0.3979 0.16 0 0 20.95 0.333 12.49 16.713 0.0803 5.72 0 11.19 65.363 0 0 0 0 0 0 0.292 5.38 20.1 0.296 10.62 10.3 5.38 4.04 16.23 0.2951 8.64 0 10.3 97.314 0 0.0772 0.0599 0.07 0.0547 0.0704 0.052 0.0301 0.1135 3.4789 0.001 NaN 0.0707 0.0211 175.2173 0.0315 1940.3994 0 0.0744 0.0546 0 0 0 0 0 0 0 0 0 0.0027 0.004 0 0 0 0 NaN NaN NaN NaN 0.0188 0 219.9453 0.0011 2.8374 0.0189 0.005 0.4269 0 0 0 0 0 0 0 0 0 0 0 0.0472 40.855 4.5152 30.9815 33.9606 22.9057 15.9525 110.2144 0.131 0 2.5883 0.001 0.0319 0.0197 0.012 0.0109 3.9321 0 1.5123 3.5811 0.1337 0.0055 3.8447 0.1077 0.0167 NaN NaN 418.1363 398.3185 496.1582 158.333 0.0373 0.0202 0.0462 0.6083 0.3032 0.02 0.0174 0.2827 0.0434 0.1342 0.2419 0.1343 0.367 0.1431 0.061 0 0 0 6.2698 0.1181 3.8208 5.3737 0.0254 1.6252 0 3.2461 18.0118 0 0 0 0 0 0 0.0752 1.5989 6.5893 0.0913 3.0911 8.4654 1.5989 1.2293 5.3406 0.0867 2.8551 0 2.9971 31.8843 NaN NaN 0 0.0215 0.0274 0.0315 0.0238 0.0206 0.0238 0.0144 0.0491 1.2708 0.0004 NaN 0.0229 0.0065 55.2039 0.0105 560.2658 0 0.017 0.0148 0.0124 0.0114 0 0 0 0 0 0 0 0.001 0.0013 0 0 0 0 NaN NaN NaN NaN 0.0055 0 61.5932 0.0003 0.9967 0.0082 0.0017 0.1437 0 0 0 0 0 0 0 0 0 0 0 0.0151 14.2396 1.4392 5.6188 3.6721 2.9329 2.1118 24.8504 29.0271 0 6.9458 2.738 5.9846 525.0965 0 3.4641 6.0544 0 53.684 2.4788 4.7141 1.7275 6.18 3.275 3.6084 18.7673 33.1562 26.3617 49.0013 10.0503 2.7073 3.1158 3.1136 44.5055 42.2737 1.3071 0.8693 1.1975 0.6288 0.9163 0.6448 1.4324 0.4576 0.1362 0 0 0 5.9396 3.2698 9.5805 2.3106 6.1463 4.0502 0 1.7924 29.9394 0 0 0 0 0 0 6.2052 311.6377 5.7277 2.7864 9.7752 63.7987 24.7625 13.6778 2.3394 31.9893 5.8142 0 1.6936 115.7408 0 613.3069 291.4842 494.6996 178.1759 843.1138 0 53.1098 0 48.2091 0.7578 NaN 2.957 2.1739 10.0261 17.1202 22.3756 0 0 0 0 0 0 0 0 0 0 0 0 64.6707 0 0 0 0 0 NaN NaN NaN NaN 1.9864 0 29.3804 0.1094 4.856 3.1406 0.5064 6.6926 0 0 0 0 0 0 0 0 0 0 0 2.057 4.0825 11.5074 0.1096 0.0078 0.0026 7.116 1.0616 395.57 75.752 0.4234 12.93 0.78 0.1827 5.7349 0.3363 39.8842 3.2687 1.0297 1.0344 0.4385 0.1039 42.3877 NaN NaN NaN NaN NaN NaN NaN NaN 533.85 2.1113 8.95 0.3157 3.0624 0.1026 1.6765 14.9509 NaN NaN NaN NaN 0.5005 0.0118 0.0035 2.363 NaN NaN NaN NaN
3095.78 2465.14 2230.4222 1463.6606 0.8294 100 102.3433 0.1247 1.4966 -0.0005 -0.0148 0.9627 200.547 0 10.1548 414.7347 9.2599 0.9701 191.2872 12.4608 1.3825 -5441.5 2604.25 -3498.75 -1640.25 1.2973 2.0143 7.39 68.4222 2.2667 0.2102 3.4171 84.9052 9.7997 50.6596 64.2828 49.3404 64.9193 87.5241 118.1188 78.25 2.773 70 352.2445 10.0373 133.1727 724.8264 1.2887 145.8445 1 631.2618 205.1695 0 4.59 4.842 2853 0.9324 0.9479 4.682 0.8073 352.0073 10.3092 113.98 10.9036 19.1927 27.6301 697.1964 1.1598 154.3709 1 620.3582 82.3494 NaN NaN 0 -0.0039 -0.0198 0.0004 -0.044 -0.0358 -0.012 -0.0377 0.0017 6.8043 0.1358 NaN 2.3754 0.9894 1931.6464 0.1874 8407.0299 0.1455 -0.0015 0 -0.0005 0.0001 0.5854 0 -0.9353 -0.0158 -0.0004 -0.0004 -0.0752 -0.0045 0.0002 0.0015 0 0.0772 -0.0903 NaN NaN NaN NaN 0.9425 0 731.2517 0.9902 58.668 0.5958 0.9731 6.5061 15.88 2.541 15.91 15.88 0.8703 2.771 0.4138 3.272 -0.0946 0.8122 0.9985 2.2932 998.1081 37.9213 98 80.3 81 56.2 219.7679 0.2301 0 5.7 0.0049 0.1356 0.06 0.0547 0.0204 12.3319 0 6.285 13.077 0.5666 0.0144 11.8428 0.35 0.0437 NaN NaN 568 59 297 3277 0.112 0.115 0.124 2.2 1.1 0.079 0.561 1.0498 0.1917 0.4115 0.6582 0.4115 1.0181 0.2315 0.325 0 0 17.99 0.439 10.14 16.358 0.0892 6.92 0 9.05 82.986 0 0 0 0 0 0 0.222 3.74 19.59 0.316 11.65 8.02 3.74 3.659 15.078 0.358 8.96 0 8.02 134.25 0 0.0566 0.0488 0.1651 0.1578 0.0468 0.0987 0.0734 0.0747 3.9578 0.005 NaN 0.0761 0.0014 128.4285 0.0238 1988 0 0.0203 0.0236 0 0 0 0 0 0 0 0 0 0.0064 0.0036 0 0 0 0 NaN NaN NaN NaN 0.0154 0 193.0287 0.0007 3.8999 0.0187 0.0086 0.5749 0 0 0 0 0 0 0 0 0 0 0 0.0411 29.743 3.6327 29.0598 28.9862 22.3163 17.4008 83.5542 0.0767 0 1.8459 0.0012 0.044 0.0171 0.0154 0.0069 3.9011 0 2.1016 3.9483 0.1662 0.0049 3.7836 0.1 0.0139 NaN NaN 233.9865 26.5879 139.2082 1529.7622 0.0502 0.0561 0.0591 0.8151 0.3464 0.0291 0.1822 0.3814 0.0715 0.1667 0.263 0.1667 0.3752 0.0856 0.1214 0 0 0 5.6522 0.1417 2.9939 5.2445 0.0264 1.8045 0 2.7661 23.623 0 0 0 0 0 0 0.0778 1.1506 5.9247 0.0878 3.3604 7.7421 1.1506 1.1265 5.0108 0.1013 2.4278 0 2.489 41.708 NaN NaN 0 0.0142 0.023 0.0768 0.0729 0.0143 0.0513 0.0399 0.0365 1.2474 0.0017 NaN 0.0248 0.0005 46.3453 0.0069 677.1873 0 0.0053 0.0059 0.0081 0.0033 0 0 0 0 0 0 0 0.0022 0.0013 0 0 0 0 NaN NaN NaN NaN 0.0049 0 65.0999 0.0002 1.1655 0.0068 0.0027 0.1921 0 0 0 0 0 0 0 0 0 0 0 0.012 10.5837 1.0323 4.3465 2.5939 3.2858 2.5197 15.015 27.7464 0 5.5695 3.93 9.0604 0 368.9713 2.1196 6.1491 0 61.8918 3.1531 6.1188 1.4857 6.1911 2.8088 3.1595 10.4383 2.2655 8.4887 199.7866 8.6336 5.7093 1.6779 3.2153 48.5294 37.5793 16.4174 1.2364 1.9562 0.8123 1.0239 0.834 1.5683 0.2645 0.2751 0 0 0 5.1072 4.3737 7.6142 2.2568 6.9233 4.7448 0 1.4336 40.4475 0 0 0 0 0 0 4.7415 463.2883 5.5652 3.0652 10.2211 73.5536 19.4865 13.243 2.1627 30.8643 5.8042 0 1.2928 163.0249 0 0 246.7762 0 359.0444 130.635 820.79 194.4371 0 58.1666 3.6822 NaN 3.2029 0.1441 6.6487 12.6788 23.6469 0 0 0 0 0 0 0 0 0 0 0 0 141.4365 0 0 0 0 0 NaN NaN NaN NaN 1.6292 0 26.397 0.0673 6.6475 3.131 0.8832 8.837 0 0 0 0 0 0 0 0 0 0 0 1.791 2.9799 9.5796 0.1096 0.0078 0.0026 7.116 1.3526 408.798 74.64 0.7193 16 1.33 0.2829 7.1196 0.4989 53.1836 3.9139 1.7819 0.9634 0.1745 0.0375 18.1087 NaN NaN NaN NaN NaN NaN NaN NaN 535.0164 2.4335 5.92 0.2653 2.0111 0.0772 1.1065 10.9003 0.0096 0.0201 0.006 208.2045 0.5019 0.0223 0.0055 4.4447 0.0096 0.0201 0.006 208.2045
2932.61 2559.94 2186.4111 1698.0172 1.5102 100 95.4878 0.1241 1.4436 0.0041 0.0013 0.9615 202.0179 0 9.5157 416.7075 9.3144 0.9674 192.7035 12.5404 1.4123 -5447.75 2701.75 -4047 -1916.5 1.3122 2.0295 7.5788 67.1333 2.3333 0.1734 3.5986 84.7569 8.659 50.153 64.1114 49.847 65.8389 84.7327 118.6128 14.37 5.434 70 364.3782 9.8783 131.8027 734.7924 1.2992 141.0845 1 637.2655 185.7574 0 4.486 4.748 2936 0.9139 0.9447 4.5873 23.8245 364.5364 10.1685 115.6273 11.3019 16.1755 24.2829 710.5095 0.8694 145.8 1 625.9636 84.7681 140.6972 485.2665 0 -0.0078 -0.0326 -0.0052 0.0213 -0.0054 -0.1134 -0.0182 0.0287 7.1041 0.1362 NaN 2.4532 0.988 1685.8514 0.1497 9317.1698 0.0553 0.0006 -0.0013 0 0.0002 -0.1343 0 -0.1427 0.1218 0.0006 -0.0001 0.0134 -0.0026 -0.0016 -0.0006 0.0013 -0.0301 -0.0728 NaN NaN NaN 0.4684 0.9231 0 718.5777 0.9899 58.4808 0.6015 0.9772 6.4527 15.9 2.882 15.94 15.95 0.8798 3.094 0.4777 3.272 -0.1892 0.8194 0.9978 2.2592 998.444 42.0579 89 126.4 96.5 45.1001 306.038 0.3263 0 8.33 0.0038 0.0754 0.0483 0.0619 0.0221 8.266 0 4.819 8.443 0.4909 0.0177 8.2054 0.47 0.0497 NaN NaN 562 788 759 2100 0.187 0.117 0.068 2.1 1.4 0.123 0.319 1.0824 0.0369 0.3141 0.5753 0.3141 0.9677 0.2706 0.326 0 0 17.78 0.745 13.31 22.912 0.1959 9.21 0 17.87 60.11 0 0 0 0 0 0 0.139 5.09 19.75 0.949 9.71 16.73 5.09 11.059 22.624 0.1164 13.3 0 16.73 79.618 0 0.0339 0.0494 0.0696 0.0406 0.0401 0.084 0.0349 0.0718 2.4266 0.0014 NaN 0.0963 0.0152 182.4956 0.0284 839.6006 0 0.0192 0.017 0 0 0 0 0 0 0 0 0 0.0062 0.004 0 0 0 0 NaN NaN NaN 0.1729 0.0273 0 104.4042 0.0007 4.1446 0.0733 0.0063 0.4166 0 0 0 0 0 0 0 0 0 0 0 0.0487 29.621 3.9133 23.551 41.3837 32.6256 15.7716 97.3868 0.1117 0 2.5274 0.0012 0.0249 0.0152 0.0157 0.0075 2.8705 0 1.5306 2.5493 0.1479 0.0059 2.8046 0.1185 0.0167 NaN NaN 251.4536 329.6406 325.0672 902.4576 0.08 0.0583 0.0326 0.6964 0.4031 0.0416 0.1041 0.3846 0.0151 0.1288 0.2268 0.1288 0.3677 0.1175 0.1261 0 0 0 5.7247 0.2682 3.8541 6.1797 0.0546 2.568 0 4.6067 16.0104 0 0 0 0 0 0 0.0243 1.5481 5.9453 0.2777 3.16 8.9855 1.5481 2.9844 6.2277 0.0353 3.7663 0 5.6983 24.7959 13.5664 15.4488 0 0.0105 0.0208 0.0327 0.0171 0.0116 0.0428 0.0154 0.0383 0.7786 0.0005 NaN 0.0302 0.0046 58.0575 0.0092 283.6616 0 0.0054 0.0043 0.003 0.0037 0 0 0 0 0 0 0 0.0021 0.0015 0 0 0 0 NaN NaN NaN 0.0221 0.01 0 28.7334 0.0003 1.2356 0.019 0.002 0.1375 0 0 0 0 0 0 0 0 0 0 0 0.019 11.4871 1.1798 4.0782 4.3102 3.7696 2.0627 18.0233 21.6062 0 8.7236 3.0609 5.2231 0 0 2.2943 4.0917 0 50.6425 2.0261 5.2707 1.8268 4.2581 3.7479 3.522 10.3162 29.1663 18.7546 109.5747 14.2503 5.765 0.8972 3.1281 60 70.9161 8.8647 1.2771 0.4264 0.6263 0.8973 0.6301 1.4698 0.3194 0.2748 0 0 0 4.8795 7.5418 10.0984 3.1182 15.079 6.528 0 2.8042 32.3594 0 0 0 0 0 0 3.0301 21.3645 5.4178 9.3327 8.3977 148.0287 31.4674 45.5423 3.1842 13.3923 9.1221 0 2.6727 93.9245 0 434.2674 151.7665 0 190.3869 746.915 74.0741 191.7582 250.1742 34.1573 1.0281 NaN 3.9238 1.5357 10.8251 18.9849 9.0113 0 0 0 0 0 0 0 0 0 0 0 0 240.7767 244.2748 0 0 0 0 NaN NaN NaN 36.9067 2.9626 0 14.5293 0.0751 7.087 12.1831 0.6451 6.4568 0 0 0 0 0 0 0 0 0 0 0 2.1538 2.9667 9.3046 0.1096 0.0078 0.0026 7.116 0.7942 411.136 74.654 0.1832 16.16 0.85 0.0857 7.1619 0.3752 23.0713 3.9306 1.1386 1.5021 0.3718 0.1233 24.7524 267.064 0.9032 1.1 0.6219 0.4122 0.2562 0.4119 68.8489 535.0245 2.0293 11.21 0.1882 4.0923 0.064 2.0952 9.2721 0.0584 0.0484 0.0148 82.8602 0.4958 0.0157 0.0039 3.1745 0.0584 0.0484 0.0148 82.8602
2988.72 2479.9 2199.0333 909.7926 1.3204 100 104.2367 0.1217 1.4882 -0.0124 -0.0033 0.9629 201.8482 0 9.6052 422.2894 9.6924 0.9687 192.1557 12.4782 1.4011 -5468.25 2648.25 -4515 -1657.25 1.3137 2.0038 7.3145 62.9333 2.6444 0.2071 3.3813 84.9105 8.6789 50.51 64.1125 49.49 65.1951 86.6867 117.0442 76.9 1.279 70 363.0273 9.9305 131.8027 733.8778 1.3027 142.5427 1 637.3727 189.9079 0 4.486 4.748 2936 0.9139 0.9447 4.5873 24.3791 361.4582 10.2112 116.1818 13.5597 15.6209 23.4736 710.4043 0.9761 147.6545 1 625.2945 70.2289 160.321 464.9735 0 -0.0555 -0.0461 -0.04 0.04 0.0676 -0.1051 0.0028 0.0277 7.5925 0.1302 NaN 2.4004 0.9904 1752.0968 0.1958 8205.7 0.0697 -0.0003 -0.0021 -0.0001 0.0002 0.0411 0 0.0177 -0.0195 -0.0002 0 -0.0699 -0.0059 0.0003 0.0003 0.0021 -0.0483 -0.118 NaN NaN NaN 0.4647 0.9564 0 709.0867 0.9906 58.6635 0.6016 0.9761 6.4935 15.55 3.132 15.61 15.59 1.366 2.48 0.5176 3.119 0.2838 0.7244 0.9961 2.3802 980.451 41.1025 127 118 123.7 47.8 162.432 0.1915 0 5.51 0.003 0.114 0.0393 0.0613 0.019 13.2651 0 9.073 15.241 1.3029 0.015 11.9738 0.35 0.0699 NaN NaN 859 355 3433 3004 0.068 0.108 0.1 1.7 0.9 0.086 0.241 0.9386 0.0356 0.2618 0.4391 0.2618 0.8567 0.2452 0.39 0 0 16.22 0.693 14.67 22.562 0.1786 5.69 0 18.2 52.571 0 0 0 0 0 0 0.139 5.92 23.6 1.264 10.63 13.56 5.92 11.382 24.32 0.3458 9.56 0 21.97 104.95 0 0.1248 0.0463 0.1223 0.0354 0.0708 0.0754 0.0643 0.0932 5.5398 0.0023 NaN 0.0764 0.0015 152.0885 0.0573 820.3999 0 0.0152 0.0149 0 0 0 0 0 0 0 0 0 0.0067 0.004 0 0 0 0 NaN NaN NaN 0.0191 0.0234 0 94.0954 0.001 3.2119 0.0406 0.0072 0.4212 0 0 0 0 0 0 0 0 0 0 0 0.0513 31.83 3.1959 33.896 37.8477 44.3906 16.9347 50.3631 0.0581 0 2.1775 0.0007 0.0417 0.0115 0.0172 0.0063 4.2154 0 2.896 4.0526 0.3882 0.0049 3.9403 0.0916 0.0245 NaN NaN 415.5048 157.0889 1572.6896 1377.4276 0.0285 0.0445 0.0465 0.6305 0.3046 0.0286 0.0824 0.3483 0.0128 0.1004 0.1701 0.1004 0.3465 0.0973 0.1675 0 0 0 5.444 0.2004 4.19 6.3329 0.0479 1.7339 0 4.966 15.7375 0 0 0 0 0 0 0.0243 1.7317 6.6262 0.3512 3.2699 9.402 1.7317 3.0672 6.6839 0.0928 3.0229 0 6.3292 29.0339 8.4026 4.8851 0 0.0407 0.0198 0.0531 0.0167 0.0224 0.0422 0.0273 0.0484 1.8222 0.0006 NaN 0.0252 0.0004 45.7058 0.0188 309.8492 0 0.0046 0.0049 0.0028 0.0034 0 0 0 0 0 0 0 0.0024 0.0014 0 0 0 0 NaN NaN NaN 0.0038 0.0068 0 32.4228 0.0003 1.1135 0.0132 0.0023 0.1348 0 0 0 0 0 0 0 0 0 0 0 0.0155 13.3972 1.1907 5.6363 3.9482 4.9881 2.1737 17.8537 14.5054 0 5.286 2.4643 7.6602 317.7362 0 1.9689 6.5718 0 94.4594 3.6091 13.442 1.5441 6.2313 2.8049 4.9898 15.7089 13.4051 76.0354 181.2641 5.176 5.3899 1.3671 2.7013 34.0336 41.5236 7.1274 1.1054 0.4097 0.5183 0.6849 0.529 1.3141 0.2829 0.3332 0 0 0 4.468 6.9785 11.1303 3.0744 13.7105 3.9918 0 2.8555 27.6824 0 0 0 0 0 0 3.0301 24.2831 6.5291 12.3786 9.1494 100.0021 37.8979 48.4887 3.4234 35.4323 6.4746 0 3.5135 149.4399 0 225.0169 100.4883 305.75 88.5553 104.666 71.7583 0 336.766 72.9635 1.767 NaN 3.1817 0.1488 8.6804 29.2542 9.9979 0 0 711.6418 0 0 0 0 0 0 0 0 0 113.5593 0 0 0 0 0 NaN NaN NaN 4.12 2.4416 0 13.2699 0.0977 5.4751 6.7553 0.7404 6.4865 0 0 0 0 0 0 0 0 0 0 0 2.1565 3.2465 7.7754 0.1096 0.0078 0.0026 7.116 1.165 372.822 72.442 1.8804 131.68 39.33 0.6812 56.9303 17.4781 161.4081 35.3198 54.2917 1.1613 0.7288 0.271 62.7572 268.228 0.6511 7.32 0.163 3.5611 0.067 2.729 25.0363 530.5682 2.0253 9.33 0.1738 2.8971 0.0525 1.7585 8.5831 0.0202 0.0149 0.0044 73.8432 0.499 0.0103 0.0025 2.0544 0.0202 0.0149 0.0044 73.8432
3032.24 2502.87 2233.3667 1326.52 1.5334 100 100.3967 0.1235 1.5031 -0.0031 -0.0072 0.9569 201.9424 0 10.5661 420.5925 10.3387 0.9735 191.6037 12.4735 1.3888 -5476.25 2635.25 -3987.5 117 1.2887 1.9912 7.2748 62.8333 3.1556 0.2696 3.2728 86.3269 8.7677 50.248 64.1511 49.752 66.1542 86.1468 121.4364 76.39 2.209 70 353.34 10.4091 176.3136 789.7523 1.0341 138.0882 1 667.7418 233.5491 0 4.624 4.894 2865 0.9298 0.9449 4.6414 -12.2945 355.0809 9.7948 144.0191 21.9782 32.2945 44.1498 745.6025 0.9256 146.6636 1 645.7636 65.8417 NaN NaN 0 -0.0534 0.0183 -0.0167 -0.0449 0.0034 -0.0178 -0.0123 -0.0048 7.5017 0.1342 NaN 2.453 0.9902 1828.3846 0.1829 9014.46 0.0448 -0.0077 -0.0001 -0.0001 -0.0001 0.2189 0 -0.6704 -0.0167 0.0004 -0.0003 0.0696 -0.0045 0.0002 0.0078 0 -0.0799 -0.2038 NaN NaN NaN NaN 0.9424 0 796.595 0.9908 58.3858 0.5913 0.9628 6.3551 15.75 3.148 15.73 15.71 0.946 3.027 0.5328 3.299 -0.5677 0.778 1.001 2.3715 993.1274 38.1448 119 143.2 123.1 48.8 296.303 0.3744 0 3.64 0.0041 0.0634 0.0451 0.0623 0.024 14.2354 0 9.005 12.506 0.4434 0.0126 13.9047 0.43 0.0538 NaN NaN 699 283 1747 1443 0.147 0.04 0.113 3.9 0.8 0.101 0.499 0.576 0.0631 0.3053 0.583 0.3053 0.8285 0.1308 0.922 0 0 15.24 0.282 10.85 37.715 0.1189 3.98 0 25.54 72.149 0 0 0 0 0 0 0.25 5.52 15.76 0.519 10.71 19.77 5.52 8.446 33.832 0.3951 9.09 0 19.77 92.307 0 0.0915 0.0506 0.0769 0.1079 0.0797 0.1047 0.0924 0.1015 4.1338 0.003 NaN 0.0802 0.0004 69.151 0.197 1406.4004 0 0.0227 0.0272 0 0 0 0 0 0 0 0 0 0.0067 0.0031 0 0 0 0 NaN NaN NaN NaN 0.024 0 149.2172 0.0006 2.5775 0.0177 0.0214 0.4051 0 0 0 0 0 0 0 0 0 0 0 0.0488 19.862 3.6163 34.125 55.9626 53.0876 17.4864 88.7672 0.1092 0 1.0929 0.0013 0.0257 0.0116 0.0163 0.008 4.4239 0 3.2376 3.6536 0.1293 0.004 4.3474 0.1275 0.0181 NaN NaN 319.1252 128.0296 799.5884 628.3083 0.0755 0.0181 0.0476 1.35 0.2698 0.032 0.1541 0.2155 0.031 0.1354 0.2194 0.1354 0.3072 0.0582 0.3574 0 0 0 4.8956 0.0766 2.913 11.0583 0.0327 1.1229 0 7.3296 23.116 0 0 0 0 0 0 0.0822 1.6216 4.7279 0.1773 3.155 9.7777 1.6216 2.5923 10.5352 0.1301 3.0939 0 6.3767 32.0537 NaN NaN 0 0.0246 0.0221 0.0329 0.0522 0.0256 0.0545 0.0476 0.0463 1.553 0.001 NaN 0.0286 0.0001 21.0312 0.0573 494.7368 0 0.0063 0.0077 0.0052 0.0027 0 0 0 0 0 0 0 0.0025 0.0012 0 0 0 0 NaN NaN NaN NaN 0.0089 0 57.2692 0.0002 0.8495 0.0065 0.0077 0.1356 0 0 0 0 0 0 0 0 0 0 0 0.0165 7.1493 1.1704 5.3823 4.7226 4.9184 2.185 22.3369 24.4142 0 3.6256 3.3208 4.2178 0 866.0295 2.5046 7.0492 0 85.2255 2.9734 4.2892 1.2943 7.257 3.4473 3.8754 12.7642 10.739 43.8119 0 11.4064 2.0088 1.5533 6.2069 25.3521 37.4691 15.247 0.6672 0.7198 0.6076 0.9088 0.6136 1.2524 0.1518 0.7592 0 0 0 4.3131 2.7092 6.1538 4.7756 11.4945 2.8822 0 3.8248 30.8924 0 0 0 0 0 0 5.3863 44.898 4.4384 5.2987 7.4365 89.9529 17.0927 19.1303 4.5375 42.6838 6.1979 0 3.0615 140.1953 0 171.4486 276.881 461.8619 240.1781 0 587.3773 748.1781 0 55.1057 2.2358 NaN 3.2712 0.0372 3.7821 107.6905 15.6016 0 293.1396 0 0 0 0 0 0 0 0 0 0 148.0663 0 0 0 0 0 NaN NaN NaN NaN 2.5512 0 18.7319 0.0616 4.4146 2.9954 2.2181 6.3745 0 0 0 0 0 0 0 0 0 0 0 2.0579 1.9999 9.4805 0.1096 0.0078 0.0026 7.116 1.4636 399.914 79.156 1.0388 19.63 1.98 0.4287 9.7608 0.8311 70.9706 4.9086 2.5014 0.9778 0.2156 0.0461 22.05 NaN NaN NaN NaN NaN NaN NaN NaN 532.0155 2.0275 8.83 0.2224 3.1776 0.0706 1.6597 10.9698 NaN NaN NaN NaN 0.48 0.4766 0.1045 99.3032 0.0202 0.0149 0.0044 73.8432
```
> 准备数据: 将value为NaN的替换为均值
```python
def replaceNanWithMean():
datMat = loadDataSet('data/13.PCA/secom.data', ' ')
numFeat = shape(datMat)[1]
for i in range(numFeat):
# 对value不为NaN的求均值
# .A 返回矩阵基于的数组
meanVal = mean(datMat[nonzero(~isnan(datMat[:, i].A))[0], i])
# 将value为NaN的值赋值为均值
datMat[nonzero(isnan(datMat[:, i].A))[0],i] = meanVal
return datMat
```
> 分析数据: 统计分析 N 的阈值
![PCA分析数据过程](http://data.apachecn.org/img/AiLearning/ml/13.PCA/PCA分析数据过程.jpg)
> PCA 数据降维
在等式 Av=入v 中，v 是特征向量， 入是特征值。<br/>
表示 如果特征向量 v 被某个矩阵 A 左乘，那么它就等于某个标量 入 乘以 v.<br/>
幸运的是: Numpy 中有寻找特征向量和特征值的模块 linalg，它有 eig() 方法，该方法用于求解特征向量和特征值。
```python
def pca(dataMat, topNfeat=9999999):
"""pca
Args:
dataMat 原数据集矩阵
topNfeat 应用的N个特征
Returns:
lowDDataMat 降维后数据集
reconMat 新的数据集空间
"""
# 计算每一列的均值
meanVals = mean(dataMat, axis=0)
# print 'meanVals', meanVals
# 每个向量同时都减去 均值
meanRemoved = dataMat - meanVals
# print 'meanRemoved=', meanRemoved
# cov协方差=[(x1-x均值)*(y1-y均值)+(x2-x均值)*(y2-y均值)+...+(xn-x均值)*(yn-y均值)+]/(n-1)
'''
方差: （一维）度量两个随机变量关系的统计量
协方差: （二维）度量各个维度偏离其均值的程度
协方差矩阵: （多维）度量各个维度偏离其均值的程度
当 cov(X, Y)>0时，表明X与Y正相关；(X越大，Y也越大；X越小Y，也越小。这种情况，我们称为“正相关”。)
当 cov(X, Y)<0时，表明X与Y负相关；
当 cov(X, Y)=0时，表明X与Y不相关。
'''
covMat = cov(meanRemoved, rowvar=0)
# eigVals为特征值， eigVects为特征向量
eigVals, eigVects = linalg.eig(mat(covMat))
# print 'eigVals=', eigVals
# print 'eigVects=', eigVects
# 对特征值，进行从小到大的排序，返回从小到大的index序号
# 特征值的逆序就可以得到topNfeat个最大的特征向量
'''
>>> x = np.array([3, 1, 2])
>>> np.argsort(x)
array([1, 2, 0]) # index,1 = 1; index,2 = 2; index,0 = 3
>>> y = np.argsort(x)
>>> y[::-1]
array([0, 2, 1])
>>> y[:-3:-1]
array([0, 2]) # 取出 -1, -2
>>> y[:-6:-1]
array([0, 2, 1])
'''
eigValInd = argsort(eigVals)
# print 'eigValInd1=', eigValInd
# -1表示倒序，返回topN的特征值[-1 到 -(topNfeat+1) 但是不包括-(topNfeat+1)本身的倒叙]
eigValInd = eigValInd[:-(topNfeat+1):-1]
# print 'eigValInd2=', eigValInd
# 重组 eigVects 最大到最小
redEigVects = eigVects[:, eigValInd]
# print 'redEigVects=', redEigVects.T
# 将数据转换到新空间
# --- (1567, 590) (590, 20)
# print "---", shape(meanRemoved), shape(redEigVects)
lowDDataMat = meanRemoved * redEigVects
reconMat = (lowDDataMat * redEigVects.T) + meanVals
# print 'lowDDataMat=', lowDDataMat
# print 'reconMat=', reconMat
return lowDDataMat, reconMat
```
[完整代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/13.PCA/pca.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/13.PCA/pca.py>
### 要点补充
```
降维技术使得数据变的更易使用，并且它们往往能够去除数据中的噪音，使得其他机器学习任务更加精确。
降维往往作为预处理步骤，在数据应用到其他算法之前清洗数据。
比较流行的降维技术: 独立成分分析、因子分析 和 主成分分析， 其中又以主成分分析应用最广泛。
本章中的PCA将所有的数据集都调入了内存，如果无法做到，就需要其他的方法来寻找其特征值。
如果使用在线PCA分析的方法，你可以参考一篇优秀的论文 "Incremental Eigenanalysis for Classification"。
下一章要讨论的奇异值分解方法也可以用于特征值分析。
```
* * *
* **作者: [片刻](http://cwiki.apachecn.org/display/~jiangzhonglian) [1988](http://cwiki.apachecn.org/display/~lihuisong)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**
# 第13章 利用 PCA 来简化数据
![利用PCA简化数据_首页](http://data.apachecn.org/img/AiLearning/ml/13.PCA/利用PCA简化数据_首页.jpg)
## 降维技术
> 场景
* 我们正通过电视观看体育比赛，在电视的显示器上有一个球。
* 显示器大概包含了100万像素点，而球则可能是由较少的像素点组成，例如说一千个像素点。
* 人们实时的将显示器上的百万像素转换成为一个三维图像，该图像就给出运动场上球的位置。
* 在这个过程中，人们已经将百万像素点的数据，降至为三维。这个过程就称为`降维(dimensionality reduction)`
> 数据显示 并非大规模特征下的唯一难题，对数据进行简化还有如下一系列的原因:
* 1) 使得数据集更容易使用
* 2) 降低很多算法的计算开销
* 3) 去除噪音
* 4) 使得结果易懂
> 适用范围:
* 在已标注与未标注的数据上都有降维技术。
* 这里我们将主要关注未标注数据上的降维技术，将技术同样也可以应用于已标注的数据。
> 在以下3种降维技术中， PCA的应用目前最为广泛，因此本章主要关注PCA。
* 1) 主成分分析(Principal Component Analysis, PCA)
* `通俗理解: 就是找出一个最主要的特征，然后进行分析。`
* `例如: 考察一个人的智力情况，就直接看数学成绩就行(存在: 数学、语文、英语成绩)`
* 2) 因子分析(Factor Analysis)
* `通俗理解: 将多个实测变量转换为少数几个综合指标。它反映一种降维的思想，通过降维将相关性高的变量聚在一起,从而减少需要分析的变量的数量,而减少问题分析的复杂性`
* `例如: 考察一个人的整体情况，就直接组合3样成绩(隐变量)，看平均成绩就行(存在: 数学、语文、英语成绩)`
* 应用的领域: 社会科学、金融和其他领域
* 在因子分析中，我们
* 假设观察数据的成分中有一些观察不到的隐变量(latent variable)。
* 假设观察数据是这些隐变量和某些噪音的线性组合。
* 那么隐变量的数据可能比观察数据的数目少，也就说通过找到隐变量就可以实现数据的降维。
* 3) 独立成分分析(Independ Component Analysis, ICA)
* `通俗理解: ICA 认为观测信号是若干个独立信号的线性组合，ICA 要做的是一个解混过程。`
* `例如: 我们去ktv唱歌，想辨别唱的是什么歌曲？ICA 是观察发现是原唱唱的一首歌【2个独立的声音（原唱／主唱）】。`
* ICA 是假设数据是从 N 个数据源混合组成的，这一点和因子分析有些类似，这些数据源之间在统计上是相互独立的，而在 PCA 中只假设数据是不 相关（线性关系）的。
* 同因子分析一样，如果数据源的数目少于观察数据的数目，则可以实现降维过程。
## PCA
### PCA 概述
主成分分析(Principal Component Analysis, PCA): `通俗理解: 就是找出一个最主要的特征，然后进行分析。`
### PCA 场景
`例如: 考察一个人的智力情况，就直接看数学成绩就行(存在: 数学、语文、英语成绩)`
### PCA 原理
> PCA 工作原理
1. 找出第一个主成分的方向，也就是数据 `方差最大` 的方向。
2. 找出第二个主成分的方向，也就是数据 `方差次大` 的方向，并且该方向与第一个主成分方向 `正交(orthogonal 如果是二维空间就叫垂直)`。
3. 通过这种方式计算出所有的主成分方向。
4. 通过数据集的协方差矩阵及其特征值分析，我们就可以得到这些主成分的值。
5. 一旦得到了协方差矩阵的特征值和特征向量，我们就可以保留最大的 N 个特征。这些特征向量也给出了 N 个最重要特征的真实结构，我们就可以通过将数据乘上这 N 个特征向量 从而将它转换到新的空间上。
为什么正交？
1. 正交是为了数据有效性损失最小
2. 正交的一个原因是特征值的特征向量是正交的
例如下图:
![应用PCA降维](http://data.apachecn.org/img/AiLearning/ml/13.PCA/应用PCA降维.png)
> PCA 优缺点
```
优点: 降低数据的复杂性，识别最重要的多个特征。
缺点: 不一定需要，且可能损失有用信息。
适用数据类型: 数值型数据。
```
### 项目案例: 对半导体数据进行降维处理
#### 项目概述
```
半导体是在一些极为先进的工厂中制造出来的。设备的生命早期有限，并且花费极其巨大。
虽然通过早期测试和频繁测试来发现有瑕疵的产品，但仍有一些存在瑕疵的产品通过测试。
如果我们通过机器学习技术用于发现瑕疵产品，那么它就会为制造商节省大量的资金。
具体来讲，它拥有590个特征。我们看看能否对这些特征进行降维处理。
对于数据的缺失值的问题，我们有一些处理方法(参考第5章)
目前该章节处理的方案是: 将缺失值NaN(Not a Number缩写)，全部用平均值来替代(如果用0来处理的策略就太差劲了)。
```
#### 开发流程
> 收集数据: 提供文本文件
文件名: secom.data
文本文件数据格式如下:
```
3030.93 2564 2187.7333 1411.1265 1.3602 100 97.6133 0.1242 1.5005 0.0162 -0.0034 0.9455 202.4396 0 7.9558 414.871 10.0433 0.968 192.3963 12.519 1.4026 -5419 2916.5 -4043.75 751 0.8955 1.773 3.049 64.2333 2.0222 0.1632 3.5191 83.3971 9.5126 50.617 64.2588 49.383 66.3141 86.9555 117.5132 61.29 4.515 70 352.7173 10.1841 130.3691 723.3092 1.3072 141.2282 1 624.3145 218.3174 0 4.592 4.841 2834 0.9317 0.9484 4.7057 -1.7264 350.9264 10.6231 108.6427 16.1445 21.7264 29.5367 693.7724 0.9226 148.6009 1 608.17 84.0793 NaN NaN 0 0.0126 -0.0206 0.0141 -0.0307 -0.0083 -0.0026 -0.0567 -0.0044 7.2163 0.132 NaN 2.3895 0.969 1747.6049 0.1841 8671.9301 -0.3274 -0.0055 -0.0001 0.0001 0.0003 -0.2786 0 0.3974 -0.0251 0.0002 0.0002 0.135 -0.0042 0.0003 0.0056 0 -0.2468 0.3196 NaN NaN NaN NaN 0.946 0 748.6115 0.9908 58.4306 0.6002 0.9804 6.3788 15.88 2.639 15.94 15.93 0.8656 3.353 0.4098 3.188 -0.0473 0.7243 0.996 2.2967 1000.7263 39.2373 123 111.3 75.2 46.2 350.671 0.3948 0 6.78 0.0034 0.0898 0.085 0.0358 0.0328 12.2566 0 4.271 10.284 0.4734 0.0167 11.8901 0.41 0.0506 NaN NaN 1017 967 1066 368 0.09 0.048 0.095 2 0.9 0.069 0.046 0.725 0.1139 0.3183 0.5888 0.3184 0.9499 0.3979 0.16 0 0 20.95 0.333 12.49 16.713 0.0803 5.72 0 11.19 65.363 0 0 0 0 0 0 0.292 5.38 20.1 0.296 10.62 10.3 5.38 4.04 16.23 0.2951 8.64 0 10.3 97.314 0 0.0772 0.0599 0.07 0.0547 0.0704 0.052 0.0301 0.1135 3.4789 0.001 NaN 0.0707 0.0211 175.2173 0.0315 1940.3994 0 0.0744 0.0546 0 0 0 0 0 0 0 0 0 0.0027 0.004 0 0 0 0 NaN NaN NaN NaN 0.0188 0 219.9453 0.0011 2.8374 0.0189 0.005 0.4269 0 0 0 0 0 0 0 0 0 0 0 0.0472 40.855 4.5152 30.9815 33.9606 22.9057 15.9525 110.2144 0.131 0 2.5883 0.001 0.0319 0.0197 0.012 0.0109 3.9321 0 1.5123 3.5811 0.1337 0.0055 3.8447 0.1077 0.0167 NaN NaN 418.1363 398.3185 496.1582 158.333 0.0373 0.0202 0.0462 0.6083 0.3032 0.02 0.0174 0.2827 0.0434 0.1342 0.2419 0.1343 0.367 0.1431 0.061 0 0 0 6.2698 0.1181 3.8208 5.3737 0.0254 1.6252 0 3.2461 18.0118 0 0 0 0 0 0 0.0752 1.5989 6.5893 0.0913 3.0911 8.4654 1.5989 1.2293 5.3406 0.0867 2.8551 0 2.9971 31.8843 NaN NaN 0 0.0215 0.0274 0.0315 0.0238 0.0206 0.0238 0.0144 0.0491 1.2708 0.0004 NaN 0.0229 0.0065 55.2039 0.0105 560.2658 0 0.017 0.0148 0.0124 0.0114 0 0 0 0 0 0 0 0.001 0.0013 0 0 0 0 NaN NaN NaN NaN 0.0055 0 61.5932 0.0003 0.9967 0.0082 0.0017 0.1437 0 0 0 0 0 0 0 0 0 0 0 0.0151 14.2396 1.4392 5.6188 3.6721 2.9329 2.1118 24.8504 29.0271 0 6.9458 2.738 5.9846 525.0965 0 3.4641 6.0544 0 53.684 2.4788 4.7141 1.7275 6.18 3.275 3.6084 18.7673 33.1562 26.3617 49.0013 10.0503 2.7073 3.1158 3.1136 44.5055 42.2737 1.3071 0.8693 1.1975 0.6288 0.9163 0.6448 1.4324 0.4576 0.1362 0 0 0 5.9396 3.2698 9.5805 2.3106 6.1463 4.0502 0 1.7924 29.9394 0 0 0 0 0 0 6.2052 311.6377 5.7277 2.7864 9.7752 63.7987 24.7625 13.6778 2.3394 31.9893 5.8142 0 1.6936 115.7408 0 613.3069 291.4842 494.6996 178.1759 843.1138 0 53.1098 0 48.2091 0.7578 NaN 2.957 2.1739 10.0261 17.1202 22.3756 0 0 0 0 0 0 0 0 0 0 0 0 64.6707 0 0 0 0 0 NaN NaN NaN NaN 1.9864 0 29.3804 0.1094 4.856 3.1406 0.5064 6.6926 0 0 0 0 0 0 0 0 0 0 0 2.057 4.0825 11.5074 0.1096 0.0078 0.0026 7.116 1.0616 395.57 75.752 0.4234 12.93 0.78 0.1827 5.7349 0.3363 39.8842 3.2687 1.0297 1.0344 0.4385 0.1039 42.3877 NaN NaN NaN NaN NaN NaN NaN NaN 533.85 2.1113 8.95 0.3157 3.0624 0.1026 1.6765 14.9509 NaN NaN NaN NaN 0.5005 0.0118 0.0035 2.363 NaN NaN NaN NaN
3095.78 2465.14 2230.4222 1463.6606 0.8294 100 102.3433 0.1247 1.4966 -0.0005 -0.0148 0.9627 200.547 0 10.1548 414.7347 9.2599 0.9701 191.2872 12.4608 1.3825 -5441.5 2604.25 -3498.75 -1640.25 1.2973 2.0143 7.39 68.4222 2.2667 0.2102 3.4171 84.9052 9.7997 50.6596 64.2828 49.3404 64.9193 87.5241 118.1188 78.25 2.773 70 352.2445 10.0373 133.1727 724.8264 1.2887 145.8445 1 631.2618 205.1695 0 4.59 4.842 2853 0.9324 0.9479 4.682 0.8073 352.0073 10.3092 113.98 10.9036 19.1927 27.6301 697.1964 1.1598 154.3709 1 620.3582 82.3494 NaN NaN 0 -0.0039 -0.0198 0.0004 -0.044 -0.0358 -0.012 -0.0377 0.0017 6.8043 0.1358 NaN 2.3754 0.9894 1931.6464 0.1874 8407.0299 0.1455 -0.0015 0 -0.0005 0.0001 0.5854 0 -0.9353 -0.0158 -0.0004 -0.0004 -0.0752 -0.0045 0.0002 0.0015 0 0.0772 -0.0903 NaN NaN NaN NaN 0.9425 0 731.2517 0.9902 58.668 0.5958 0.9731 6.5061 15.88 2.541 15.91 15.88 0.8703 2.771 0.4138 3.272 -0.0946 0.8122 0.9985 2.2932 998.1081 37.9213 98 80.3 81 56.2 219.7679 0.2301 0 5.7 0.0049 0.1356 0.06 0.0547 0.0204 12.3319 0 6.285 13.077 0.5666 0.0144 11.8428 0.35 0.0437 NaN NaN 568 59 297 3277 0.112 0.115 0.124 2.2 1.1 0.079 0.561 1.0498 0.1917 0.4115 0.6582 0.4115 1.0181 0.2315 0.325 0 0 17.99 0.439 10.14 16.358 0.0892 6.92 0 9.05 82.986 0 0 0 0 0 0 0.222 3.74 19.59 0.316 11.65 8.02 3.74 3.659 15.078 0.358 8.96 0 8.02 134.25 0 0.0566 0.0488 0.1651 0.1578 0.0468 0.0987 0.0734 0.0747 3.9578 0.005 NaN 0.0761 0.0014 128.4285 0.0238 1988 0 0.0203 0.0236 0 0 0 0 0 0 0 0 0 0.0064 0.0036 0 0 0 0 NaN NaN NaN NaN 0.0154 0 193.0287 0.0007 3.8999 0.0187 0.0086 0.5749 0 0 0 0 0 0 0 0 0 0 0 0.0411 29.743 3.6327 29.0598 28.9862 22.3163 17.4008 83.5542 0.0767 0 1.8459 0.0012 0.044 0.0171 0.0154 0.0069 3.9011 0 2.1016 3.9483 0.1662 0.0049 3.7836 0.1 0.0139 NaN NaN 233.9865 26.5879 139.2082 1529.7622 0.0502 0.0561 0.0591 0.8151 0.3464 0.0291 0.1822 0.3814 0.0715 0.1667 0.263 0.1667 0.3752 0.0856 0.1214 0 0 0 5.6522 0.1417 2.9939 5.2445 0.0264 1.8045 0 2.7661 23.623 0 0 0 0 0 0 0.0778 1.1506 5.9247 0.0878 3.3604 7.7421 1.1506 1.1265 5.0108 0.1013 2.4278 0 2.489 41.708 NaN NaN 0 0.0142 0.023 0.0768 0.0729 0.0143 0.0513 0.0399 0.0365 1.2474 0.0017 NaN 0.0248 0.0005 46.3453 0.0069 677.1873 0 0.0053 0.0059 0.0081 0.0033 0 0 0 0 0 0 0 0.0022 0.0013 0 0 0 0 NaN NaN NaN NaN 0.0049 0 65.0999 0.0002 1.1655 0.0068 0.0027 0.1921 0 0 0 0 0 0 0 0 0 0 0 0.012 10.5837 1.0323 4.3465 2.5939 3.2858 2.5197 15.015 27.7464 0 5.5695 3.93 9.0604 0 368.9713 2.1196 6.1491 0 61.8918 3.1531 6.1188 1.4857 6.1911 2.8088 3.1595 10.4383 2.2655 8.4887 199.7866 8.6336 5.7093 1.6779 3.2153 48.5294 37.5793 16.4174 1.2364 1.9562 0.8123 1.0239 0.834 1.5683 0.2645 0.2751 0 0 0 5.1072 4.3737 7.6142 2.2568 6.9233 4.7448 0 1.4336 40.4475 0 0 0 0 0 0 4.7415 463.2883 5.5652 3.0652 10.2211 73.5536 19.4865 13.243 2.1627 30.8643 5.8042 0 1.2928 163.0249 0 0 246.7762 0 359.0444 130.635 820.79 194.4371 0 58.1666 3.6822 NaN 3.2029 0.1441 6.6487 12.6788 23.6469 0 0 0 0 0 0 0 0 0 0 0 0 141.4365 0 0 0 0 0 NaN NaN NaN NaN 1.6292 0 26.397 0.0673 6.6475 3.131 0.8832 8.837 0 0 0 0 0 0 0 0 0 0 0 1.791 2.9799 9.5796 0.1096 0.0078 0.0026 7.116 1.3526 408.798 74.64 0.7193 16 1.33 0.2829 7.1196 0.4989 53.1836 3.9139 1.7819 0.9634 0.1745 0.0375 18.1087 NaN NaN NaN NaN NaN NaN NaN NaN 535.0164 2.4335 5.92 0.2653 2.0111 0.0772 1.1065 10.9003 0.0096 0.0201 0.006 208.2045 0.5019 0.0223 0.0055 4.4447 0.0096 0.0201 0.006 208.2045
2932.61 2559.94 2186.4111 1698.0172 1.5102 100 95.4878 0.1241 1.4436 0.0041 0.0013 0.9615 202.0179 0 9.5157 416.7075 9.3144 0.9674 192.7035 12.5404 1.4123 -5447.75 2701.75 -4047 -1916.5 1.3122 2.0295 7.5788 67.1333 2.3333 0.1734 3.5986 84.7569 8.659 50.153 64.1114 49.847 65.8389 84.7327 118.6128 14.37 5.434 70 364.3782 9.8783 131.8027 734.7924 1.2992 141.0845 1 637.2655 185.7574 0 4.486 4.748 2936 0.9139 0.9447 4.5873 23.8245 364.5364 10.1685 115.6273 11.3019 16.1755 24.2829 710.5095 0.8694 145.8 1 625.9636 84.7681 140.6972 485.2665 0 -0.0078 -0.0326 -0.0052 0.0213 -0.0054 -0.1134 -0.0182 0.0287 7.1041 0.1362 NaN 2.4532 0.988 1685.8514 0.1497 9317.1698 0.0553 0.0006 -0.0013 0 0.0002 -0.1343 0 -0.1427 0.1218 0.0006 -0.0001 0.0134 -0.0026 -0.0016 -0.0006 0.0013 -0.0301 -0.0728 NaN NaN NaN 0.4684 0.9231 0 718.5777 0.9899 58.4808 0.6015 0.9772 6.4527 15.9 2.882 15.94 15.95 0.8798 3.094 0.4777 3.272 -0.1892 0.8194 0.9978 2.2592 998.444 42.0579 89 126.4 96.5 45.1001 306.038 0.3263 0 8.33 0.0038 0.0754 0.0483 0.0619 0.0221 8.266 0 4.819 8.443 0.4909 0.0177 8.2054 0.47 0.0497 NaN NaN 562 788 759 2100 0.187 0.117 0.068 2.1 1.4 0.123 0.319 1.0824 0.0369 0.3141 0.5753 0.3141 0.9677 0.2706 0.326 0 0 17.78 0.745 13.31 22.912 0.1959 9.21 0 17.87 60.11 0 0 0 0 0 0 0.139 5.09 19.75 0.949 9.71 16.73 5.09 11.059 22.624 0.1164 13.3 0 16.73 79.618 0 0.0339 0.0494 0.0696 0.0406 0.0401 0.084 0.0349 0.0718 2.4266 0.0014 NaN 0.0963 0.0152 182.4956 0.0284 839.6006 0 0.0192 0.017 0 0 0 0 0 0 0 0 0 0.0062 0.004 0 0 0 0 NaN NaN NaN 0.1729 0.0273 0 104.4042 0.0007 4.1446 0.0733 0.0063 0.4166 0 0 0 0 0 0 0 0 0 0 0 0.0487 29.621 3.9133 23.551 41.3837 32.6256 15.7716 97.3868 0.1117 0 2.5274 0.0012 0.0249 0.0152 0.0157 0.0075 2.8705 0 1.5306 2.5493 0.1479 0.0059 2.8046 0.1185 0.0167 NaN NaN 251.4536 329.6406 325.0672 902.4576 0.08 0.0583 0.0326 0.6964 0.4031 0.0416 0.1041 0.3846 0.0151 0.1288 0.2268 0.1288 0.3677 0.1175 0.1261 0 0 0 5.7247 0.2682 3.8541 6.1797 0.0546 2.568 0 4.6067 16.0104 0 0 0 0 0 0 0.0243 1.5481 5.9453 0.2777 3.16 8.9855 1.5481 2.9844 6.2277 0.0353 3.7663 0 5.6983 24.7959 13.5664 15.4488 0 0.0105 0.0208 0.0327 0.0171 0.0116 0.0428 0.0154 0.0383 0.7786 0.0005 NaN 0.0302 0.0046 58.0575 0.0092 283.6616 0 0.0054 0.0043 0.003 0.0037 0 0 0 0 0 0 0 0.0021 0.0015 0 0 0 0 NaN NaN NaN 0.0221 0.01 0 28.7334 0.0003 1.2356 0.019 0.002 0.1375 0 0 0 0 0 0 0 0 0 0 0 0.019 11.4871 1.1798 4.0782 4.3102 3.7696 2.0627 18.0233 21.6062 0 8.7236 3.0609 5.2231 0 0 2.2943 4.0917 0 50.6425 2.0261 5.2707 1.8268 4.2581 3.7479 3.522 10.3162 29.1663 18.7546 109.5747 14.2503 5.765 0.8972 3.1281 60 70.9161 8.8647 1.2771 0.4264 0.6263 0.8973 0.6301 1.4698 0.3194 0.2748 0 0 0 4.8795 7.5418 10.0984 3.1182 15.079 6.528 0 2.8042 32.3594 0 0 0 0 0 0 3.0301 21.3645 5.4178 9.3327 8.3977 148.0287 31.4674 45.5423 3.1842 13.3923 9.1221 0 2.6727 93.9245 0 434.2674 151.7665 0 190.3869 746.915 74.0741 191.7582 250.1742 34.1573 1.0281 NaN 3.9238 1.5357 10.8251 18.9849 9.0113 0 0 0 0 0 0 0 0 0 0 0 0 240.7767 244.2748 0 0 0 0 NaN NaN NaN 36.9067 2.9626 0 14.5293 0.0751 7.087 12.1831 0.6451 6.4568 0 0 0 0 0 0 0 0 0 0 0 2.1538 2.9667 9.3046 0.1096 0.0078 0.0026 7.116 0.7942 411.136 74.654 0.1832 16.16 0.85 0.0857 7.1619 0.3752 23.0713 3.9306 1.1386 1.5021 0.3718 0.1233 24.7524 267.064 0.9032 1.1 0.6219 0.4122 0.2562 0.4119 68.8489 535.0245 2.0293 11.21 0.1882 4.0923 0.064 2.0952 9.2721 0.0584 0.0484 0.0148 82.8602 0.4958 0.0157 0.0039 3.1745 0.0584 0.0484 0.0148 82.8602
2988.72 2479.9 2199.0333 909.7926 1.3204 100 104.2367 0.1217 1.4882 -0.0124 -0.0033 0.9629 201.8482 0 9.6052 422.2894 9.6924 0.9687 192.1557 12.4782 1.4011 -5468.25 2648.25 -4515 -1657.25 1.3137 2.0038 7.3145 62.9333 2.6444 0.2071 3.3813 84.9105 8.6789 50.51 64.1125 49.49 65.1951 86.6867 117.0442 76.9 1.279 70 363.0273 9.9305 131.8027 733.8778 1.3027 142.5427 1 637.3727 189.9079 0 4.486 4.748 2936 0.9139 0.9447 4.5873 24.3791 361.4582 10.2112 116.1818 13.5597 15.6209 23.4736 710.4043 0.9761 147.6545 1 625.2945 70.2289 160.321 464.9735 0 -0.0555 -0.0461 -0.04 0.04 0.0676 -0.1051 0.0028 0.0277 7.5925 0.1302 NaN 2.4004 0.9904 1752.0968 0.1958 8205.7 0.0697 -0.0003 -0.0021 -0.0001 0.0002 0.0411 0 0.0177 -0.0195 -0.0002 0 -0.0699 -0.0059 0.0003 0.0003 0.0021 -0.0483 -0.118 NaN NaN NaN 0.4647 0.9564 0 709.0867 0.9906 58.6635 0.6016 0.9761 6.4935 15.55 3.132 15.61 15.59 1.366 2.48 0.5176 3.119 0.2838 0.7244 0.9961 2.3802 980.451 41.1025 127 118 123.7 47.8 162.432 0.1915 0 5.51 0.003 0.114 0.0393 0.0613 0.019 13.2651 0 9.073 15.241 1.3029 0.015 11.9738 0.35 0.0699 NaN NaN 859 355 3433 3004 0.068 0.108 0.1 1.7 0.9 0.086 0.241 0.9386 0.0356 0.2618 0.4391 0.2618 0.8567 0.2452 0.39 0 0 16.22 0.693 14.67 22.562 0.1786 5.69 0 18.2 52.571 0 0 0 0 0 0 0.139 5.92 23.6 1.264 10.63 13.56 5.92 11.382 24.32 0.3458 9.56 0 21.97 104.95 0 0.1248 0.0463 0.1223 0.0354 0.0708 0.0754 0.0643 0.0932 5.5398 0.0023 NaN 0.0764 0.0015 152.0885 0.0573 820.3999 0 0.0152 0.0149 0 0 0 0 0 0 0 0 0 0.0067 0.004 0 0 0 0 NaN NaN NaN 0.0191 0.0234 0 94.0954 0.001 3.2119 0.0406 0.0072 0.4212 0 0 0 0 0 0 0 0 0 0 0 0.0513 31.83 3.1959 33.896 37.8477 44.3906 16.9347 50.3631 0.0581 0 2.1775 0.0007 0.0417 0.0115 0.0172 0.0063 4.2154 0 2.896 4.0526 0.3882 0.0049 3.9403 0.0916 0.0245 NaN NaN 415.5048 157.0889 1572.6896 1377.4276 0.0285 0.0445 0.0465 0.6305 0.3046 0.0286 0.0824 0.3483 0.0128 0.1004 0.1701 0.1004 0.3465 0.0973 0.1675 0 0 0 5.444 0.2004 4.19 6.3329 0.0479 1.7339 0 4.966 15.7375 0 0 0 0 0 0 0.0243 1.7317 6.6262 0.3512 3.2699 9.402 1.7317 3.0672 6.6839 0.0928 3.0229 0 6.3292 29.0339 8.4026 4.8851 0 0.0407 0.0198 0.0531 0.0167 0.0224 0.0422 0.0273 0.0484 1.8222 0.0006 NaN 0.0252 0.0004 45.7058 0.0188 309.8492 0 0.0046 0.0049 0.0028 0.0034 0 0 0 0 0 0 0 0.0024 0.0014 0 0 0 0 NaN NaN NaN 0.0038 0.0068 0 32.4228 0.0003 1.1135 0.0132 0.0023 0.1348 0 0 0 0 0 0 0 0 0 0 0 0.0155 13.3972 1.1907 5.6363 3.9482 4.9881 2.1737 17.8537 14.5054 0 5.286 2.4643 7.6602 317.7362 0 1.9689 6.5718 0 94.4594 3.6091 13.442 1.5441 6.2313 2.8049 4.9898 15.7089 13.4051 76.0354 181.2641 5.176 5.3899 1.3671 2.7013 34.0336 41.5236 7.1274 1.1054 0.4097 0.5183 0.6849 0.529 1.3141 0.2829 0.3332 0 0 0 4.468 6.9785 11.1303 3.0744 13.7105 3.9918 0 2.8555 27.6824 0 0 0 0 0 0 3.0301 24.2831 6.5291 12.3786 9.1494 100.0021 37.8979 48.4887 3.4234 35.4323 6.4746 0 3.5135 149.4399 0 225.0169 100.4883 305.75 88.5553 104.666 71.7583 0 336.766 72.9635 1.767 NaN 3.1817 0.1488 8.6804 29.2542 9.9979 0 0 711.6418 0 0 0 0 0 0 0 0 0 113.5593 0 0 0 0 0 NaN NaN NaN 4.12 2.4416 0 13.2699 0.0977 5.4751 6.7553 0.7404 6.4865 0 0 0 0 0 0 0 0 0 0 0 2.1565 3.2465 7.7754 0.1096 0.0078 0.0026 7.116 1.165 372.822 72.442 1.8804 131.68 39.33 0.6812 56.9303 17.4781 161.4081 35.3198 54.2917 1.1613 0.7288 0.271 62.7572 268.228 0.6511 7.32 0.163 3.5611 0.067 2.729 25.0363 530.5682 2.0253 9.33 0.1738 2.8971 0.0525 1.7585 8.5831 0.0202 0.0149 0.0044 73.8432 0.499 0.0103 0.0025 2.0544 0.0202 0.0149 0.0044 73.8432
3032.24 2502.87 2233.3667 1326.52 1.5334 100 100.3967 0.1235 1.5031 -0.0031 -0.0072 0.9569 201.9424 0 10.5661 420.5925 10.3387 0.9735 191.6037 12.4735 1.3888 -5476.25 2635.25 -3987.5 117 1.2887 1.9912 7.2748 62.8333 3.1556 0.2696 3.2728 86.3269 8.7677 50.248 64.1511 49.752 66.1542 86.1468 121.4364 76.39 2.209 70 353.34 10.4091 176.3136 789.7523 1.0341 138.0882 1 667.7418 233.5491 0 4.624 4.894 2865 0.9298 0.9449 4.6414 -12.2945 355.0809 9.7948 144.0191 21.9782 32.2945 44.1498 745.6025 0.9256 146.6636 1 645.7636 65.8417 NaN NaN 0 -0.0534 0.0183 -0.0167 -0.0449 0.0034 -0.0178 -0.0123 -0.0048 7.5017 0.1342 NaN 2.453 0.9902 1828.3846 0.1829 9014.46 0.0448 -0.0077 -0.0001 -0.0001 -0.0001 0.2189 0 -0.6704 -0.0167 0.0004 -0.0003 0.0696 -0.0045 0.0002 0.0078 0 -0.0799 -0.2038 NaN NaN NaN NaN 0.9424 0 796.595 0.9908 58.3858 0.5913 0.9628 6.3551 15.75 3.148 15.73 15.71 0.946 3.027 0.5328 3.299 -0.5677 0.778 1.001 2.3715 993.1274 38.1448 119 143.2 123.1 48.8 296.303 0.3744 0 3.64 0.0041 0.0634 0.0451 0.0623 0.024 14.2354 0 9.005 12.506 0.4434 0.0126 13.9047 0.43 0.0538 NaN NaN 699 283 1747 1443 0.147 0.04 0.113 3.9 0.8 0.101 0.499 0.576 0.0631 0.3053 0.583 0.3053 0.8285 0.1308 0.922 0 0 15.24 0.282 10.85 37.715 0.1189 3.98 0 25.54 72.149 0 0 0 0 0 0 0.25 5.52 15.76 0.519 10.71 19.77 5.52 8.446 33.832 0.3951 9.09 0 19.77 92.307 0 0.0915 0.0506 0.0769 0.1079 0.0797 0.1047 0.0924 0.1015 4.1338 0.003 NaN 0.0802 0.0004 69.151 0.197 1406.4004 0 0.0227 0.0272 0 0 0 0 0 0 0 0 0 0.0067 0.0031 0 0 0 0 NaN NaN NaN NaN 0.024 0 149.2172 0.0006 2.5775 0.0177 0.0214 0.4051 0 0 0 0 0 0 0 0 0 0 0 0.0488 19.862 3.6163 34.125 55.9626 53.0876 17.4864 88.7672 0.1092 0 1.0929 0.0013 0.0257 0.0116 0.0163 0.008 4.4239 0 3.2376 3.6536 0.1293 0.004 4.3474 0.1275 0.0181 NaN NaN 319.1252 128.0296 799.5884 628.3083 0.0755 0.0181 0.0476 1.35 0.2698 0.032 0.1541 0.2155 0.031 0.1354 0.2194 0.1354 0.3072 0.0582 0.3574 0 0 0 4.8956 0.0766 2.913 11.0583 0.0327 1.1229 0 7.3296 23.116 0 0 0 0 0 0 0.0822 1.6216 4.7279 0.1773 3.155 9.7777 1.6216 2.5923 10.5352 0.1301 3.0939 0 6.3767 32.0537 NaN NaN 0 0.0246 0.0221 0.0329 0.0522 0.0256 0.0545 0.0476 0.0463 1.553 0.001 NaN 0.0286 0.0001 21.0312 0.0573 494.7368 0 0.0063 0.0077 0.0052 0.0027 0 0 0 0 0 0 0 0.0025 0.0012 0 0 0 0 NaN NaN NaN NaN 0.0089 0 57.2692 0.0002 0.8495 0.0065 0.0077 0.1356 0 0 0 0 0 0 0 0 0 0 0 0.0165 7.1493 1.1704 5.3823 4.7226 4.9184 2.185 22.3369 24.4142 0 3.6256 3.3208 4.2178 0 866.0295 2.5046 7.0492 0 85.2255 2.9734 4.2892 1.2943 7.257 3.4473 3.8754 12.7642 10.739 43.8119 0 11.4064 2.0088 1.5533 6.2069 25.3521 37.4691 15.247 0.6672 0.7198 0.6076 0.9088 0.6136 1.2524 0.1518 0.7592 0 0 0 4.3131 2.7092 6.1538 4.7756 11.4945 2.8822 0 3.8248 30.8924 0 0 0 0 0 0 5.3863 44.898 4.4384 5.2987 7.4365 89.9529 17.0927 19.1303 4.5375 42.6838 6.1979 0 3.0615 140.1953 0 171.4486 276.881 461.8619 240.1781 0 587.3773 748.1781 0 55.1057 2.2358 NaN 3.2712 0.0372 3.7821 107.6905 15.6016 0 293.1396 0 0 0 0 0 0 0 0 0 0 148.0663 0 0 0 0 0 NaN NaN NaN NaN 2.5512 0 18.7319 0.0616 4.4146 2.9954 2.2181 6.3745 0 0 0 0 0 0 0 0 0 0 0 2.0579 1.9999 9.4805 0.1096 0.0078 0.0026 7.116 1.4636 399.914 79.156 1.0388 19.63 1.98 0.4287 9.7608 0.8311 70.9706 4.9086 2.5014 0.9778 0.2156 0.0461 22.05 NaN NaN NaN NaN NaN NaN NaN NaN 532.0155 2.0275 8.83 0.2224 3.1776 0.0706 1.6597 10.9698 NaN NaN NaN NaN 0.48 0.4766 0.1045 99.3032 0.0202 0.0149 0.0044 73.8432
```
> 准备数据: 将value为NaN的替换为均值
```python
def replaceNanWithMean():
datMat = loadDataSet('data/13.PCA/secom.data', ' ')
numFeat = shape(datMat)[1]
for i in range(numFeat):
# 对value不为NaN的求均值
# .A 返回矩阵基于的数组
meanVal = mean(datMat[nonzero(~isnan(datMat[:, i].A))[0], i])
# 将value为NaN的值赋值为均值
datMat[nonzero(isnan(datMat[:, i].A))[0],i] = meanVal
return datMat
```
> 分析数据: 统计分析 N 的阈值
![PCA分析数据过程](http://data.apachecn.org/img/AiLearning/ml/13.PCA/PCA分析数据过程.jpg)
> PCA 数据降维
在等式 Av=入v 中，v 是特征向量， 入是特征值。<br/>
表示 如果特征向量 v 被某个矩阵 A 左乘，那么它就等于某个标量 入 乘以 v.<br/>
幸运的是: Numpy 中有寻找特征向量和特征值的模块 linalg，它有 eig() 方法，该方法用于求解特征向量和特征值。
```python
def pca(dataMat, topNfeat=9999999):
"""pca
Args:
dataMat 原数据集矩阵
topNfeat 应用的N个特征
Returns:
lowDDataMat 降维后数据集
reconMat 新的数据集空间
"""
# 计算每一列的均值
meanVals = mean(dataMat, axis=0)
# print 'meanVals', meanVals
# 每个向量同时都减去 均值
meanRemoved = dataMat - meanVals
# print 'meanRemoved=', meanRemoved
# cov协方差=[(x1-x均值)*(y1-y均值)+(x2-x均值)*(y2-y均值)+...+(xn-x均值)*(yn-y均值)+]/(n-1)
'''
方差: （一维）度量两个随机变量关系的统计量
协方差: （二维）度量各个维度偏离其均值的程度
协方差矩阵: （多维）度量各个维度偏离其均值的程度
当 cov(X, Y)>0时，表明X与Y正相关；(X越大，Y也越大；X越小Y，也越小。这种情况，我们称为“正相关”。)
当 cov(X, Y)<0时，表明X与Y负相关；
当 cov(X, Y)=0时，表明X与Y不相关。
'''
covMat = cov(meanRemoved, rowvar=0)
# eigVals为特征值， eigVects为特征向量
eigVals, eigVects = linalg.eig(mat(covMat))
# print 'eigVals=', eigVals
# print 'eigVects=', eigVects
# 对特征值，进行从小到大的排序，返回从小到大的index序号
# 特征值的逆序就可以得到topNfeat个最大的特征向量
'''
>>> x = np.array([3, 1, 2])
>>> np.argsort(x)
array([1, 2, 0]) # index,1 = 1; index,2 = 2; index,0 = 3
>>> y = np.argsort(x)
>>> y[::-1]
array([0, 2, 1])
>>> y[:-3:-1]
array([0, 2]) # 取出 -1, -2
>>> y[:-6:-1]
array([0, 2, 1])
'''
eigValInd = argsort(eigVals)
# print 'eigValInd1=', eigValInd
# -1表示倒序，返回topN的特征值[-1 到 -(topNfeat+1) 但是不包括-(topNfeat+1)本身的倒叙]
eigValInd = eigValInd[:-(topNfeat+1):-1]
# print 'eigValInd2=', eigValInd
# 重组 eigVects 最大到最小
redEigVects = eigVects[:, eigValInd]
# print 'redEigVects=', redEigVects.T
# 将数据转换到新空间
# --- (1567, 590) (590, 20)
# print "---", shape(meanRemoved), shape(redEigVects)
lowDDataMat = meanRemoved * redEigVects
reconMat = (lowDDataMat * redEigVects.T) + meanVals
# print 'lowDDataMat=', lowDDataMat
# print 'reconMat=', reconMat
return lowDDataMat, reconMat
```
[完整代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/13.PCA/pca.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/13.PCA/pca.py>
### 要点补充
```
降维技术使得数据变的更易使用，并且它们往往能够去除数据中的噪音，使得其他机器学习任务更加精确。
降维往往作为预处理步骤，在数据应用到其他算法之前清洗数据。
比较流行的降维技术: 独立成分分析、因子分析 和 主成分分析， 其中又以主成分分析应用最广泛。
本章中的PCA将所有的数据集都调入了内存，如果无法做到，就需要其他的方法来寻找其特征值。
如果使用在线PCA分析的方法，你可以参考一篇优秀的论文 "Incremental Eigenanalysis for Classification"。
下一章要讨论的奇异值分解方法也可以用于特征值分析。
```
* * *
* **作者: [片刻](http://cwiki.apachecn.org/display/~jiangzhonglian) [1988](http://cwiki.apachecn.org/display/~lihuisong)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**

876
docs/ml/14.利用SVD简化数据.md → docs/ml/14.md
View File

@@ -1,438 +1,438 @@
# 第14章 利用SVD简化数据
<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=default"></script>
![利用SVD简化数据首页](http://data.apachecn.org/img/AiLearning/ml/14.SVD/svd_headPage.jpg "利用SVD简化数据首页")
## SVD 概述
```
奇异值分解（SVD, Singular Value Decomposition）:
提取信息的一种方法，可以把 SVD 看成是从噪声数据中抽取相关特征。从生物信息学到金融学，SVD 是提取信息的强大工具。
```
## SVD 场景
> 信息检索-隐性语义检索（Latent Semantic Indexing, LSI）或 隐形语义分析（Latent Semantic Analysis, LSA）
隐性语义索引: 矩阵 = 文档 + 词语
* 是最早的 SVD 应用之一，我们称利用 SVD 的方法为隐性语义索引（LSI）或隐性语义分析（LSA）。
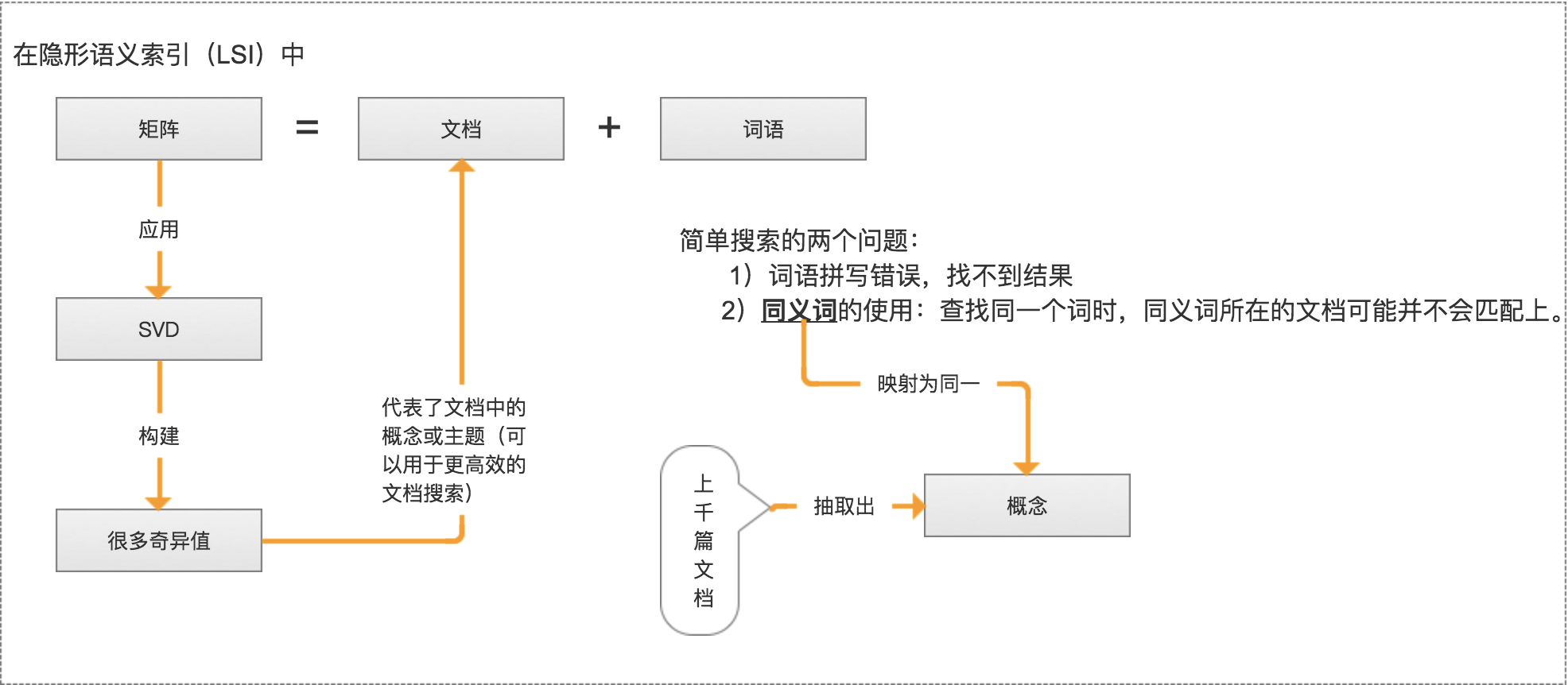
![LSA举例](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-LSI举例.png)
> 推荐系统
1. 利用 SVD 从数据中构建一个主题空间。
2. 再在该空间下计算其相似度。(从高维-低维空间的转化，在低维空间来计算相似度，SVD 提升了推荐系统的效率。)
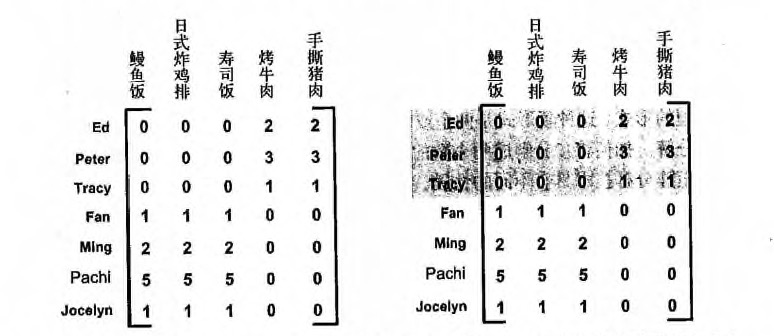
![主题空间案例1](http://data.apachecn.org/img/AiLearning/ml/14.SVD/SVD_推荐系统_主题空间案例1.jpg)
* 上图右边标注的为一组共同特征，表示美式 BBQ 空间；另一组在上图右边未标注的为日式食品 空间。
> 图像压缩
例如: `32*32=1024 => 32*2+2*1+32*2=130`(2*1表示去掉了除对角线的0), 几乎获得了10倍的压缩比。
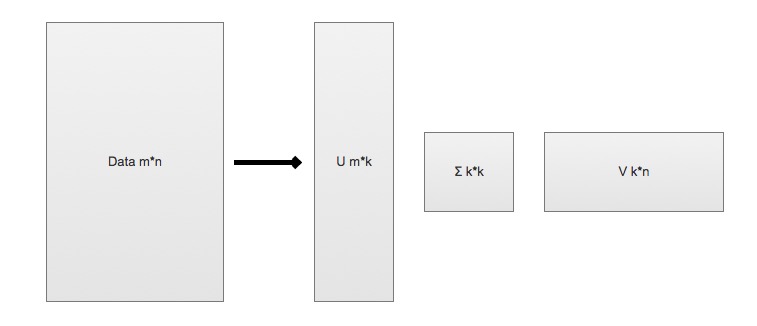
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-SVD公式.jpg)
## SVD 原理
### SVD 工作原理
> 矩阵分解
* 矩阵分解是将数据矩阵分解为多个独立部分的过程。
* 矩阵分解可以将原始矩阵表示成新的易于处理的形式，这种新形式是两个或多个矩阵的乘积。（类似代数中的因数分解）
* 举例: 如何将12分解成两个数的乘积？（1，12）、（2，6）、（3，4）都是合理的答案。
> SVD 是矩阵分解的一种类型，也是矩阵分解最常见的技术
* SVD 将原始的数据集矩阵 Data 分解成三个矩阵 U、$$\sum$$、V
* 举例: 如果原始矩阵 $$Data_{m \ast n}$$ 是m行n列，
* $$U_{m \ast k}$$ 表示m行k列
* $$\sum_{k \ast k}$$ 表示k行k列
* $$V_{k \ast n}$$ 表示k行n列。
$$Data_{m \ast n} = U_{m \ast k} \sum_{k \ast k} V_{k \ast n}$$
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-SVD公式.jpg)
具体的案例: （大家可以试着推导一下: https://wenku.baidu.com/view/b7641217866fb84ae45c8d17.html ）
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/SVD公式的测试案例.jpg)
* 上述分解中会构建出一个矩阵 $$\sum$$ ，该矩阵只有对角元素，其他元素均为0(近似于0)。另一个惯例就是，$$\sum$$ 的对角元素是从大到小排列的。这些对角元素称为奇异值。
* 奇异值与特征值(PCA 数据中重要特征)是有关系的。这里的奇异值就是矩阵 $$Data \ast Data^T$$ 特征值的平方根。
* 普遍的事实: 在某个奇异值的数目(r 个=>奇异值的平方和累加到总值的90%以上)之后，其他的奇异值都置为0(近似于0)。这意味着数据集中仅有 r 个重要特征，而其余特征则都是噪声或冗余特征。
### SVD 算法特点
```
优点: 简化数据，去除噪声，优化算法的结果
缺点: 数据的转换可能难以理解
使用的数据类型: 数值型数据
```
## 推荐系统
### 推荐系统 概述
`推荐系统是利用电子商务网站向客户提供商品信息和建议，帮助用户决定应该购买什么产品，模拟销售人员帮助客户完成购买过程。`
### 推荐系统 场景
1. Amazon 会根据顾客的购买历史向他们推荐物品
2. Netflix 会向其用户推荐电影
3. 新闻网站会对用户推荐新闻频道
### 推荐系统 要点
> 基于协同过滤(collaborative filtering) 的推荐引擎
* 利用Python 实现 SVD(Numpy 有一个称为 linalg 的线性代数工具箱)
* 协同过滤: 是通过将用户和其他用户的数据进行对比来实现推荐的。
* 当知道了两个用户或两个物品之间的相似度，我们就可以利用已有的数据来预测未知用户的喜好。
> 基于物品的相似度和基于用户的相似度: 物品比较少则选择物品相似度，用户比较少则选择用户相似度。【矩阵还是小一点好计算】
* 基于物品的相似度: 计算物品之间的距离。【耗时会随物品数量的增加而增加】
* 由于物品A和物品C 相似度(相关度)很高，所以给买A的人推荐C。
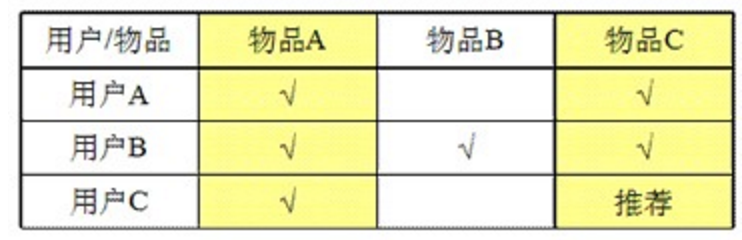
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-基于物品相似度.png)
* 基于用户的相似度: 计算用户之间的距离。【耗时会随用户数量的增加而增加】
* 由于用户A和用户C 相似度(相关度)很高，所以A和C是兴趣相投的人，对于C买的物品就会推荐给A。
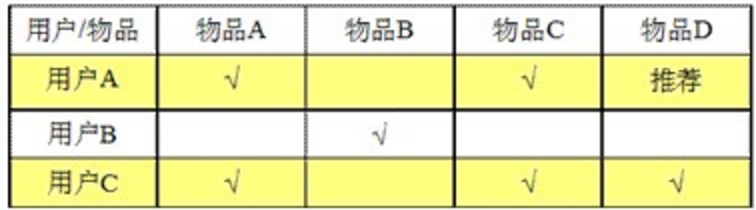
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-基于用户相似度.png)
> 相似度计算
* inA, inB 对应的是 列向量
1. 欧氏距离: 指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。二维或三维中的欧氏距离就是两点之间的实际距离。
* 相似度= 1/(1+欧式距离)
* `相似度= 1.0/(1.0 + la.norm(inA - inB))`
* 物品对越相似，它们的相似度值就越大。
2. 皮尔逊相关系数: 度量的是两个向量之间的相似度。
* 相似度= 0.5 + 0.5*corrcoef() 【皮尔逊相关系数的取值范围从 -1 到 +1，通过函数0.5 + 0.5\*corrcoef()这个函数计算，把值归一化到0到1之间】
* `相似度= 0.5 + 0.5 * corrcoef(inA, inB, rowvar = 0)[0][1]`
* 相对欧氏距离的优势: 它对用户评级的量级并不敏感。
3. 余弦相似度: 计算的是两个向量夹角的余弦值。
* 余弦值 = (A·B)/(||A||·||B||) 【余弦值的取值范围也在-1到+1之间】
* 相似度= 0.5 + 0.5*余弦值
* `相似度= 0.5 + 0.5*( float(inA.T*inB) / la.norm(inA)*la.norm(inB))`
* 如果夹角为90度，则相似度为0；如果两个向量的方向相同，则相似度为1.0。
> 推荐系统的评价
* 采用交叉测试的方法。【拆分数据为训练集和测试集】
* 推荐引擎评价的指标: 最小均方根误差(Root mean squared error, RMSE)，也称标准误差(Standard error)，就是计算均方误差的平均值然后取其平方根。
* 如果RMSE=1, 表示相差1个星级；如果RMSE=2.5, 表示相差2.5个星级。
### 推荐系统 原理
* 推荐系统的工作过程: 给定一个用户，系统会为此用户返回N个最好的推荐菜。
* 实现流程大致如下:
1. 寻找用户没有评级的菜肴，即在用户-物品矩阵中的0值。
2. 在用户没有评级的所有物品中，对每个物品预计一个可能的评级分数。这就是说: 我们认为用户可能会对物品的打分（这就是相似度计算的初衷）。
3. 对这些物品的评分从高到低进行排序，返回前N个物品。
### 项目案例: 餐馆菜肴推荐系统
#### 项目概述
`假如一个人在家决定外出吃饭，但是他并不知道该到哪儿去吃饭，该点什么菜。推荐系统可以帮他做到这两点。`
#### 开发流程
> 收集 并 准备数据
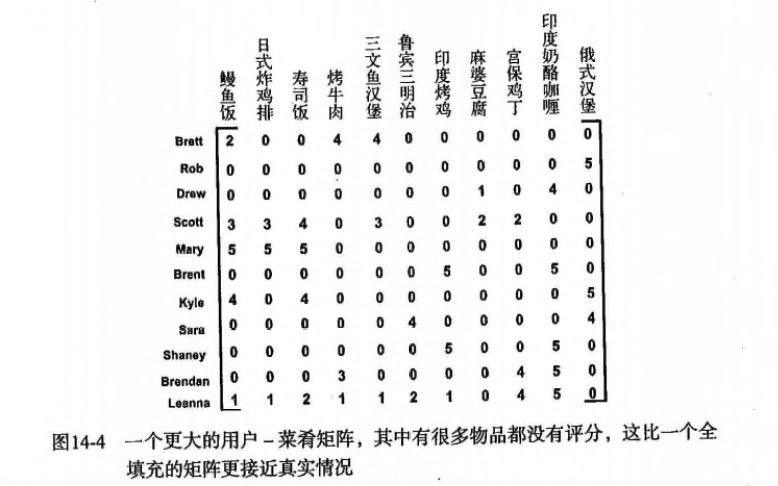
![SVD 矩阵](http://data.apachecn.org/img/AiLearning/ml/14.SVD/项目数据导入.jpg)
```python
def loadExData3():
# 利用SVD提高推荐效果，菜肴矩阵
"""
行: 代表人
列: 代表菜肴名词
值: 代表人对菜肴的评分，0表示未评分
"""
return[[2, 0, 0, 4, 4, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 4, 0],
[3, 3, 4, 0, 3, 0, 0, 2, 2, 0, 0],
[5, 5, 5, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
[4, 0, 4, 0, 0, 0, 0, 0, 0, 0, 5],
[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 4],
[0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
[0, 0, 0, 3, 0, 0, 0, 0, 4, 5, 0],
[1, 1, 2, 1, 1, 2, 1, 0, 4, 5, 0]]
```
> 分析数据: 这里不做过多的讨论(当然此处可以对比不同距离之间的差别)
> 训练算法: 通过调用 recommend() 函数进行推荐
recommend() 会调用 基于物品相似度 或者是 基于SVD，得到推荐的物品评分。
* 1.基于物品相似度
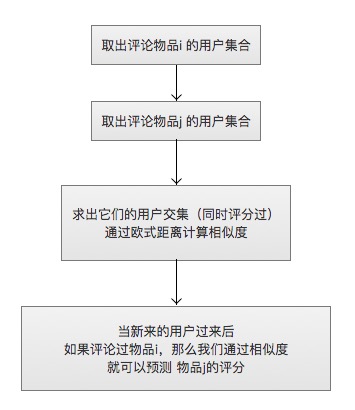
![基于物品相似度](http://data.apachecn.org/img/AiLearning/ml/14.SVD/基于物品相似度.jpg)
![欧式距离的计算方式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/欧式距离的计算方式.jpg)
```python
# 基于物品相似度的推荐引擎
def standEst(dataMat, user, simMeas, item):
"""standEst(计算某用户未评分物品中，以对该物品和其他物品评分的用户的物品相似度，然后进行综合评分)
Args:
dataMat 训练数据集
user 用户编号
simMeas 相似度计算方法
item 未评分的物品编号
Returns:
ratSimTotal/simTotal 评分（0～5之间的值）
"""
# 得到数据集中的物品数目
n = shape(dataMat)[1]
# 初始化两个评分值
simTotal = 0.0
ratSimTotal = 0.0
# 遍历行中的每个物品（对用户评过分的物品进行遍历，并将它与其他物品进行比较）
for j in range(n):
userRating = dataMat[user, j]
# 如果某个物品的评分值为0，则跳过这个物品
if userRating == 0:
continue
# 寻找两个用户都评级的物品
# 变量 overLap 给出的是两个物品当中已经被评分的那个元素的索引ID
# logical_and 计算x1和x2元素的真值。
overLap = nonzero(logical_and(dataMat[:, item].A > 0, dataMat[:, j].A > 0))[0]
# 如果相似度为0，则两着没有任何重合元素，终止本次循环
if len(overLap) == 0:
similarity = 0
# 如果存在重合的物品，则基于这些重合物重新计算相似度。
else:
similarity = simMeas(dataMat[overLap, item], dataMat[overLap, j])
# print 'the %d and %d similarity is : %f'(iten,j,similarity)
# 相似度会不断累加，每次计算时还考虑相似度和当前用户评分的乘积
# similarity 用户相似度， userRating 用户评分
simTotal += similarity
ratSimTotal += similarity * userRating
if simTotal == 0:
return 0
# 通过除以所有的评分总和，对上述相似度评分的乘积进行归一化，使得最后评分在0~5之间，这些评分用来对预测值进行排序
else:
return ratSimTotal/simTotal
```
* 2.基于SVD(参考地址: http://www.codeweblog.com/svd-%E7%AC%94%E8%AE%B0/)
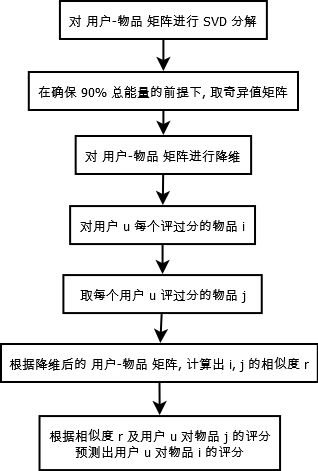
![基于SVD.png](http://data.apachecn.org/img/AiLearning/ml/14.SVD/基于SVD.png)
```python
# 基于SVD的评分估计
# 在recommend() 中，这个函数用于替换对standEst()的调用，该函数对给定用户给定物品构建了一个评分估计值
def svdEst(dataMat, user, simMeas, item):
"""svdEst(计算某用户未评分物品中，以对该物品和其他物品评分的用户的物品相似度，然后进行综合评分)
Args:
dataMat 训练数据集
user 用户编号
simMeas 相似度计算方法
item 未评分的物品编号
Returns:
ratSimTotal/simTotal 评分（0～5之间的值）
"""
# 物品数目
n = shape(dataMat)[1]
# 对数据集进行SVD分解
simTotal = 0.0
ratSimTotal = 0.0
# 奇异值分解
# 在SVD分解之后，我们只利用包含了90%能量值的奇异值，这些奇异值会以NumPy数组的形式得以保存
U, Sigma, VT = la.svd(dataMat)
# # 分析 Sigma 的长度取值
# analyse_data(Sigma, 20)
# 如果要进行矩阵运算，就必须要用这些奇异值构建出一个对角矩阵
Sig4 = mat(eye(4) * Sigma[: 4])
# 利用U矩阵将物品转换到低维空间中，构建转换后的物品(物品+4个主要的“隐形”特征)
# 公式1(目的是: 降维-改变形状，也改变大小) xformedItems = dataMat.T * U[:, :4] * Sig4.I
# 公式2(目的是: 压缩-不改变形状，改变大小) reconMat = U[:, :4] * Sig4.I * VT[:4, :]
# 其中: imgCompress() 是详细的案例
# 最近看到一篇文章描述，感觉挺有道理的，我就顺便补充一下注释: https://blog.csdn.net/qq_36523839/article/details/82347332
xformedItems = dataMat.T * U[:, :4] * Sig4.I
# 对于给定的用户，for循环在用户对应行的元素上进行遍历，
# 这和standEst()函数中的for循环的目的一样，只不过这里的相似度计算时在低维空间下进行的。
for j in range(n):
userRating = dataMat[user, j]
if userRating == 0 or j == item:
continue
# 相似度的计算方法也会作为一个参数传递给该函数
similarity = simMeas(xformedItems[item, :].T, xformedItems[j, :].T)
# for 循环中加入了一条print语句，以便了解相似度计算的进展情况。如果觉得累赘，可以去掉
print 'the %d and %d similarity is: %f' % (item, j, similarity)
# 对相似度不断累加求和
simTotal += similarity
# 对相似度及对应评分值的乘积求和
ratSimTotal += similarity * userRating
if simTotal == 0:
return 0
else:
# 计算估计评分
return ratSimTotal/simTotal
```
排序获取最后的推荐结果
```python
# recommend()函数，就是推荐引擎，它默认调用standEst()函数，产生了最高的N个推荐结果。
# 如果不指定N的大小，则默认值为3。该函数另外的参数还包括相似度计算方法和估计方法
def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
# 寻找未评级的物品
# 对给定的用户建立一个未评分的物品列表
unratedItems = nonzero(dataMat[user, :].A == 0)[1]
# 如果不存在未评分物品，那么就退出函数
if len(unratedItems) == 0:
return 'you rated everything'
# 物品的编号和评分值
itemScores = []
# 在未评分物品上进行循环
for item in unratedItems:
estimatedScore = estMethod(dataMat, user, simMeas, item)
# 寻找前N个未评级物品，调用standEst()来产生该物品的预测得分，该物品的编号和估计值会放在一个元素列表itemScores中
itemScores.append((item, estimatedScore))
# 按照估计得分，对该列表进行排序并返回。列表逆排序，第一个值就是最大值
return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[: N]
```
> 测试 和 项目调用，可直接参考我们的代码
[完整代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/14.SVD/svdRecommend.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/14.SVD/svdRecommend.py>
#### 要点补充
> 基于内容(content-based)的推荐
1. 通过各种标签来标记菜肴
2. 将这些属性作为相似度计算所需要的数据
3. 这就是: 基于内容的推荐。
> 构建推荐引擎面临的挑战
问题
* 1）在大规模的数据集上，SVD分解会降低程序的速度
* 2）存在其他很多规模扩展性的挑战性问题，比如矩阵的表示方法和计算相似度得分消耗资源。
* 3）如何在缺乏数据时给出好的推荐-称为冷启动【简单说: 用户不会喜欢一个无效的物品，而用户不喜欢的物品又无效】
建议
* 1）在大型系统中，SVD分解(可以在程序调入时运行一次)每天运行一次或者其频率更低，并且还要离线运行。
* 2）在实际中，另一个普遍的做法就是离线计算并保存相似度得分。(物品相似度可能被用户重复的调用)
* 3）冷启动问题，解决方案就是将推荐看成是搜索问题，通过各种标签／属性特征进行`基于内容的推荐`。
### 项目案例: 基于 SVD 的图像压缩
> 收集 并 准备数据
将文本数据转化为矩阵
```python
# 加载并转换数据
def imgLoadData(filename):
myl = []
# 打开文本文件，并从文件以数组方式读入字符
for line in open(filename).readlines():
newRow = []
for i in range(32):
newRow.append(int(line[i]))
myl.append(newRow)
# 矩阵调入后，就可以在屏幕上输出该矩阵
myMat = mat(myl)
return myMat
```
> 分析数据: 分析 Sigma 的长度个数
通常保留矩阵 80% ～ 90% 的能量，就可以得到重要的特征并去除噪声。
```python
def analyse_data(Sigma, loopNum=20):
"""analyse_data(分析 Sigma 的长度取值)
Args:
Sigma Sigma的值
loopNum 循环次数
"""
# 总方差的集合（总能量值）
Sig2 = Sigma**2
SigmaSum = sum(Sig2)
for i in range(loopNum):
SigmaI = sum(Sig2[:i+1])
'''
根据自己的业务情况，就行处理，设置对应的 Singma 次数
通常保留矩阵 80% ～ 90% 的能量，就可以得到重要的特征并取出噪声。
'''
print '主成分: %s, 方差占比: %s%%' % (format(i+1, '2.0f'), format(SigmaI/SigmaSum*100, '4.2f'))
```
> 使用算法: 对比使用 SVD 前后的数据差异对比，对于存储大家可以试着写写
例如: `32*32=1024 => 32*2+2*1+32*2=130`(2*1表示去掉了除对角线的0), 几乎获得了10倍的压缩比。
```python
# 打印矩阵
def printMat(inMat, thresh=0.8):
# 由于矩阵保护了浮点数，因此定义浅色和深色，遍历所有矩阵元素，当元素大于阀值时打印1，否则打印0
for i in range(32):
for k in range(32):
if float(inMat[i, k]) > thresh:
print 1,
else:
print 0,
print ''
# 实现图像压缩，允许基于任意给定的奇异值数目来重构图像
def imgCompress(numSV=3, thresh=0.8):
"""imgCompress( )
Args:
numSV Sigma长度
thresh 判断的阈值
"""
# 构建一个列表
myMat = imgLoadData('data/14.SVD/0_5.txt')
print "****original matrix****"
# 对原始图像进行SVD分解并重构图像e
printMat(myMat, thresh)
# 通过Sigma 重新构成SigRecom来实现
# Sigma是一个对角矩阵，因此需要建立一个全0矩阵，然后将前面的那些奇异值填充到对角线上。
U, Sigma, VT = la.svd(myMat)
# SigRecon = mat(zeros((numSV, numSV)))
# for k in range(numSV):
# SigRecon[k, k] = Sigma[k]
# 分析插入的 Sigma 长度
analyse_data(Sigma, 20)
SigRecon = mat(eye(numSV) * Sigma[: numSV])
reconMat = U[:, :numSV] * SigRecon * VT[:numSV, :]
print "****reconstructed matrix using %d singular values *****" % numSV
printMat(reconMat, thresh)
```
[完整代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/14.SVD/svdRecommend.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/14.SVD/svdRecommend.py>
* * *
* **作者: [片刻](http://cwiki.apachecn.org/display/~jiangzhonglian) [1988](http://cwiki.apachecn.org/display/~lihuisong)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**
# 第14章 利用SVD简化数据
<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=default"></script>
![利用SVD简化数据首页](http://data.apachecn.org/img/AiLearning/ml/14.SVD/svd_headPage.jpg "利用SVD简化数据首页")
## SVD 概述
```
奇异值分解（SVD, Singular Value Decomposition）:
提取信息的一种方法，可以把 SVD 看成是从噪声数据中抽取相关特征。从生物信息学到金融学，SVD 是提取信息的强大工具。
```
## SVD 场景
> 信息检索-隐性语义检索（Latent Semantic Indexing, LSI）或 隐形语义分析（Latent Semantic Analysis, LSA）
隐性语义索引: 矩阵 = 文档 + 词语
* 是最早的 SVD 应用之一，我们称利用 SVD 的方法为隐性语义索引（LSI）或隐性语义分析（LSA）。
![LSA举例](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-LSI举例.png)
> 推荐系统
1. 利用 SVD 从数据中构建一个主题空间。
2. 再在该空间下计算其相似度。(从高维-低维空间的转化，在低维空间来计算相似度，SVD 提升了推荐系统的效率。)
![主题空间案例1](http://data.apachecn.org/img/AiLearning/ml/14.SVD/SVD_推荐系统_主题空间案例1.jpg)
* 上图右边标注的为一组共同特征，表示美式 BBQ 空间；另一组在上图右边未标注的为日式食品 空间。
> 图像压缩
例如: `32*32=1024 => 32*2+2*1+32*2=130`(2*1表示去掉了除对角线的0), 几乎获得了10倍的压缩比。
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-SVD公式.jpg)
## SVD 原理
### SVD 工作原理
> 矩阵分解
* 矩阵分解是将数据矩阵分解为多个独立部分的过程。
* 矩阵分解可以将原始矩阵表示成新的易于处理的形式，这种新形式是两个或多个矩阵的乘积。（类似代数中的因数分解）
* 举例: 如何将12分解成两个数的乘积？（1，12）、（2，6）、（3，4）都是合理的答案。
> SVD 是矩阵分解的一种类型，也是矩阵分解最常见的技术
* SVD 将原始的数据集矩阵 Data 分解成三个矩阵 U、$$\sum$$、V
* 举例: 如果原始矩阵 $$Data_{m \ast n}$$ 是m行n列，
* $$U_{m \ast k}$$ 表示m行k列
* $$\sum_{k \ast k}$$ 表示k行k列
* $$V_{k \ast n}$$ 表示k行n列。
$$Data_{m \ast n} = U_{m \ast k} \sum_{k \ast k} V_{k \ast n}$$
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-SVD公式.jpg)
具体的案例: （大家可以试着推导一下: https://wenku.baidu.com/view/b7641217866fb84ae45c8d17.html ）
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/SVD公式的测试案例.jpg)
* 上述分解中会构建出一个矩阵 $$\sum$$ ，该矩阵只有对角元素，其他元素均为0(近似于0)。另一个惯例就是，$$\sum$$ 的对角元素是从大到小排列的。这些对角元素称为奇异值。
* 奇异值与特征值(PCA 数据中重要特征)是有关系的。这里的奇异值就是矩阵 $$Data \ast Data^T$$ 特征值的平方根。
* 普遍的事实: 在某个奇异值的数目(r 个=>奇异值的平方和累加到总值的90%以上)之后，其他的奇异值都置为0(近似于0)。这意味着数据集中仅有 r 个重要特征，而其余特征则都是噪声或冗余特征。
### SVD 算法特点
```
优点: 简化数据，去除噪声，优化算法的结果
缺点: 数据的转换可能难以理解
使用的数据类型: 数值型数据
```
## 推荐系统
### 推荐系统 概述
`推荐系统是利用电子商务网站向客户提供商品信息和建议，帮助用户决定应该购买什么产品，模拟销售人员帮助客户完成购买过程。`
### 推荐系统 场景
1. Amazon 会根据顾客的购买历史向他们推荐物品
2. Netflix 会向其用户推荐电影
3. 新闻网站会对用户推荐新闻频道
### 推荐系统 要点
> 基于协同过滤(collaborative filtering) 的推荐引擎
* 利用Python 实现 SVD(Numpy 有一个称为 linalg 的线性代数工具箱)
* 协同过滤: 是通过将用户和其他用户的数据进行对比来实现推荐的。
* 当知道了两个用户或两个物品之间的相似度，我们就可以利用已有的数据来预测未知用户的喜好。
> 基于物品的相似度和基于用户的相似度: 物品比较少则选择物品相似度，用户比较少则选择用户相似度。【矩阵还是小一点好计算】
* 基于物品的相似度: 计算物品之间的距离。【耗时会随物品数量的增加而增加】
* 由于物品A和物品C 相似度(相关度)很高，所以给买A的人推荐C。
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-基于物品相似度.png)
* 基于用户的相似度: 计算用户之间的距离。【耗时会随用户数量的增加而增加】
* 由于用户A和用户C 相似度(相关度)很高，所以A和C是兴趣相投的人，对于C买的物品就会推荐给A。
![SVD公式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/使用SVD简化数据-基于用户相似度.png)
> 相似度计算
* inA, inB 对应的是 列向量
1. 欧氏距离: 指在m维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。二维或三维中的欧氏距离就是两点之间的实际距离。
* 相似度= 1/(1+欧式距离)
* `相似度= 1.0/(1.0 + la.norm(inA - inB))`
* 物品对越相似，它们的相似度值就越大。
2. 皮尔逊相关系数: 度量的是两个向量之间的相似度。
* 相似度= 0.5 + 0.5*corrcoef() 【皮尔逊相关系数的取值范围从 -1 到 +1，通过函数0.5 + 0.5\*corrcoef()这个函数计算，把值归一化到0到1之间】
* `相似度= 0.5 + 0.5 * corrcoef(inA, inB, rowvar = 0)[0][1]`
* 相对欧氏距离的优势: 它对用户评级的量级并不敏感。
3. 余弦相似度: 计算的是两个向量夹角的余弦值。
* 余弦值 = (A·B)/(||A||·||B||) 【余弦值的取值范围也在-1到+1之间】
* 相似度= 0.5 + 0.5*余弦值
* `相似度= 0.5 + 0.5*( float(inA.T*inB) / la.norm(inA)*la.norm(inB))`
* 如果夹角为90度，则相似度为0；如果两个向量的方向相同，则相似度为1.0。
> 推荐系统的评价
* 采用交叉测试的方法。【拆分数据为训练集和测试集】
* 推荐引擎评价的指标: 最小均方根误差(Root mean squared error, RMSE)，也称标准误差(Standard error)，就是计算均方误差的平均值然后取其平方根。
* 如果RMSE=1, 表示相差1个星级；如果RMSE=2.5, 表示相差2.5个星级。
### 推荐系统 原理
* 推荐系统的工作过程: 给定一个用户，系统会为此用户返回N个最好的推荐菜。
* 实现流程大致如下:
1. 寻找用户没有评级的菜肴，即在用户-物品矩阵中的0值。
2. 在用户没有评级的所有物品中，对每个物品预计一个可能的评级分数。这就是说: 我们认为用户可能会对物品的打分（这就是相似度计算的初衷）。
3. 对这些物品的评分从高到低进行排序，返回前N个物品。
### 项目案例: 餐馆菜肴推荐系统
#### 项目概述
`假如一个人在家决定外出吃饭，但是他并不知道该到哪儿去吃饭，该点什么菜。推荐系统可以帮他做到这两点。`
#### 开发流程
> 收集 并 准备数据
![SVD 矩阵](http://data.apachecn.org/img/AiLearning/ml/14.SVD/项目数据导入.jpg)
```python
def loadExData3():
# 利用SVD提高推荐效果，菜肴矩阵
"""
行: 代表人
列: 代表菜肴名词
值: 代表人对菜肴的评分，0表示未评分
"""
return[[2, 0, 0, 4, 4, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 5],
[0, 0, 0, 0, 0, 0, 0, 1, 0, 4, 0],
[3, 3, 4, 0, 3, 0, 0, 2, 2, 0, 0],
[5, 5, 5, 0, 0, 0, 0, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
[4, 0, 4, 0, 0, 0, 0, 0, 0, 0, 5],
[0, 0, 0, 0, 0, 4, 0, 0, 0, 0, 4],
[0, 0, 0, 0, 0, 0, 5, 0, 0, 5, 0],
[0, 0, 0, 3, 0, 0, 0, 0, 4, 5, 0],
[1, 1, 2, 1, 1, 2, 1, 0, 4, 5, 0]]
```
> 分析数据: 这里不做过多的讨论(当然此处可以对比不同距离之间的差别)
> 训练算法: 通过调用 recommend() 函数进行推荐
recommend() 会调用 基于物品相似度 或者是 基于SVD，得到推荐的物品评分。
* 1.基于物品相似度
![基于物品相似度](http://data.apachecn.org/img/AiLearning/ml/14.SVD/基于物品相似度.jpg)
![欧式距离的计算方式](http://data.apachecn.org/img/AiLearning/ml/14.SVD/欧式距离的计算方式.jpg)
```python
# 基于物品相似度的推荐引擎
def standEst(dataMat, user, simMeas, item):
"""standEst(计算某用户未评分物品中，以对该物品和其他物品评分的用户的物品相似度，然后进行综合评分)
Args:
dataMat 训练数据集
user 用户编号
simMeas 相似度计算方法
item 未评分的物品编号
Returns:
ratSimTotal/simTotal 评分（0～5之间的值）
"""
# 得到数据集中的物品数目
n = shape(dataMat)[1]
# 初始化两个评分值
simTotal = 0.0
ratSimTotal = 0.0
# 遍历行中的每个物品（对用户评过分的物品进行遍历，并将它与其他物品进行比较）
for j in range(n):
userRating = dataMat[user, j]
# 如果某个物品的评分值为0，则跳过这个物品
if userRating == 0:
continue
# 寻找两个用户都评级的物品
# 变量 overLap 给出的是两个物品当中已经被评分的那个元素的索引ID
# logical_and 计算x1和x2元素的真值。
overLap = nonzero(logical_and(dataMat[:, item].A > 0, dataMat[:, j].A > 0))[0]
# 如果相似度为0，则两着没有任何重合元素，终止本次循环
if len(overLap) == 0:
similarity = 0
# 如果存在重合的物品，则基于这些重合物重新计算相似度。
else:
similarity = simMeas(dataMat[overLap, item], dataMat[overLap, j])
# print 'the %d and %d similarity is : %f'(iten,j,similarity)
# 相似度会不断累加，每次计算时还考虑相似度和当前用户评分的乘积
# similarity 用户相似度， userRating 用户评分
simTotal += similarity
ratSimTotal += similarity * userRating
if simTotal == 0:
return 0
# 通过除以所有的评分总和，对上述相似度评分的乘积进行归一化，使得最后评分在0~5之间，这些评分用来对预测值进行排序
else:
return ratSimTotal/simTotal
```
* 2.基于SVD(参考地址: http://www.codeweblog.com/svd-%E7%AC%94%E8%AE%B0/)
![基于SVD.png](http://data.apachecn.org/img/AiLearning/ml/14.SVD/基于SVD.png)
```python
# 基于SVD的评分估计
# 在recommend() 中，这个函数用于替换对standEst()的调用，该函数对给定用户给定物品构建了一个评分估计值
def svdEst(dataMat, user, simMeas, item):
"""svdEst(计算某用户未评分物品中，以对该物品和其他物品评分的用户的物品相似度，然后进行综合评分)
Args:
dataMat 训练数据集
user 用户编号
simMeas 相似度计算方法
item 未评分的物品编号
Returns:
ratSimTotal/simTotal 评分（0～5之间的值）
"""
# 物品数目
n = shape(dataMat)[1]
# 对数据集进行SVD分解
simTotal = 0.0
ratSimTotal = 0.0
# 奇异值分解
# 在SVD分解之后，我们只利用包含了90%能量值的奇异值，这些奇异值会以NumPy数组的形式得以保存
U, Sigma, VT = la.svd(dataMat)
# # 分析 Sigma 的长度取值
# analyse_data(Sigma, 20)
# 如果要进行矩阵运算，就必须要用这些奇异值构建出一个对角矩阵
Sig4 = mat(eye(4) * Sigma[: 4])
# 利用U矩阵将物品转换到低维空间中，构建转换后的物品(物品+4个主要的“隐形”特征)
# 公式1(目的是: 降维-改变形状，也改变大小) xformedItems = dataMat.T * U[:, :4] * Sig4.I
# 公式2(目的是: 压缩-不改变形状，改变大小) reconMat = U[:, :4] * Sig4.I * VT[:4, :]
# 其中: imgCompress() 是详细的案例
# 最近看到一篇文章描述，感觉挺有道理的，我就顺便补充一下注释: https://blog.csdn.net/qq_36523839/article/details/82347332
xformedItems = dataMat.T * U[:, :4] * Sig4.I
# 对于给定的用户，for循环在用户对应行的元素上进行遍历，
# 这和standEst()函数中的for循环的目的一样，只不过这里的相似度计算时在低维空间下进行的。
for j in range(n):
userRating = dataMat[user, j]
if userRating == 0 or j == item:
continue
# 相似度的计算方法也会作为一个参数传递给该函数
similarity = simMeas(xformedItems[item, :].T, xformedItems[j, :].T)
# for 循环中加入了一条print语句，以便了解相似度计算的进展情况。如果觉得累赘，可以去掉
print 'the %d and %d similarity is: %f' % (item, j, similarity)
# 对相似度不断累加求和
simTotal += similarity
# 对相似度及对应评分值的乘积求和
ratSimTotal += similarity * userRating
if simTotal == 0:
return 0
else:
# 计算估计评分
return ratSimTotal/simTotal
```
排序获取最后的推荐结果
```python
# recommend()函数，就是推荐引擎，它默认调用standEst()函数，产生了最高的N个推荐结果。
# 如果不指定N的大小，则默认值为3。该函数另外的参数还包括相似度计算方法和估计方法
def recommend(dataMat, user, N=3, simMeas=cosSim, estMethod=standEst):
# 寻找未评级的物品
# 对给定的用户建立一个未评分的物品列表
unratedItems = nonzero(dataMat[user, :].A == 0)[1]
# 如果不存在未评分物品，那么就退出函数
if len(unratedItems) == 0:
return 'you rated everything'
# 物品的编号和评分值
itemScores = []
# 在未评分物品上进行循环
for item in unratedItems:
estimatedScore = estMethod(dataMat, user, simMeas, item)
# 寻找前N个未评级物品，调用standEst()来产生该物品的预测得分，该物品的编号和估计值会放在一个元素列表itemScores中
itemScores.append((item, estimatedScore))
# 按照估计得分，对该列表进行排序并返回。列表逆排序，第一个值就是最大值
return sorted(itemScores, key=lambda jj: jj[1], reverse=True)[: N]
```
> 测试 和 项目调用，可直接参考我们的代码
[完整代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/14.SVD/svdRecommend.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/14.SVD/svdRecommend.py>
#### 要点补充
> 基于内容(content-based)的推荐
1. 通过各种标签来标记菜肴
2. 将这些属性作为相似度计算所需要的数据
3. 这就是: 基于内容的推荐。
> 构建推荐引擎面临的挑战
问题
* 1）在大规模的数据集上，SVD分解会降低程序的速度
* 2）存在其他很多规模扩展性的挑战性问题，比如矩阵的表示方法和计算相似度得分消耗资源。
* 3）如何在缺乏数据时给出好的推荐-称为冷启动【简单说: 用户不会喜欢一个无效的物品，而用户不喜欢的物品又无效】
建议
* 1）在大型系统中，SVD分解(可以在程序调入时运行一次)每天运行一次或者其频率更低，并且还要离线运行。
* 2）在实际中，另一个普遍的做法就是离线计算并保存相似度得分。(物品相似度可能被用户重复的调用)
* 3）冷启动问题，解决方案就是将推荐看成是搜索问题，通过各种标签／属性特征进行`基于内容的推荐`。
### 项目案例: 基于 SVD 的图像压缩
> 收集 并 准备数据
将文本数据转化为矩阵
```python
# 加载并转换数据
def imgLoadData(filename):
myl = []
# 打开文本文件，并从文件以数组方式读入字符
for line in open(filename).readlines():
newRow = []
for i in range(32):
newRow.append(int(line[i]))
myl.append(newRow)
# 矩阵调入后，就可以在屏幕上输出该矩阵
myMat = mat(myl)
return myMat
```
> 分析数据: 分析 Sigma 的长度个数
通常保留矩阵 80% ～ 90% 的能量，就可以得到重要的特征并去除噪声。
```python
def analyse_data(Sigma, loopNum=20):
"""analyse_data(分析 Sigma 的长度取值)
Args:
Sigma Sigma的值
loopNum 循环次数
"""
# 总方差的集合（总能量值）
Sig2 = Sigma**2
SigmaSum = sum(Sig2)
for i in range(loopNum):
SigmaI = sum(Sig2[:i+1])
'''
根据自己的业务情况，就行处理，设置对应的 Singma 次数
通常保留矩阵 80% ～ 90% 的能量，就可以得到重要的特征并取出噪声。
'''
print '主成分: %s, 方差占比: %s%%' % (format(i+1, '2.0f'), format(SigmaI/SigmaSum*100, '4.2f'))
```
> 使用算法: 对比使用 SVD 前后的数据差异对比，对于存储大家可以试着写写
例如: `32*32=1024 => 32*2+2*1+32*2=130`(2*1表示去掉了除对角线的0), 几乎获得了10倍的压缩比。
```python
# 打印矩阵
def printMat(inMat, thresh=0.8):
# 由于矩阵保护了浮点数，因此定义浅色和深色，遍历所有矩阵元素，当元素大于阀值时打印1，否则打印0
for i in range(32):
for k in range(32):
if float(inMat[i, k]) > thresh:
print 1,
else:
print 0,
print ''
# 实现图像压缩，允许基于任意给定的奇异值数目来重构图像
def imgCompress(numSV=3, thresh=0.8):
"""imgCompress( )
Args:
numSV Sigma长度
thresh 判断的阈值
"""
# 构建一个列表
myMat = imgLoadData('data/14.SVD/0_5.txt')
print "****original matrix****"
# 对原始图像进行SVD分解并重构图像e
printMat(myMat, thresh)
# 通过Sigma 重新构成SigRecom来实现
# Sigma是一个对角矩阵，因此需要建立一个全0矩阵，然后将前面的那些奇异值填充到对角线上。
U, Sigma, VT = la.svd(myMat)
# SigRecon = mat(zeros((numSV, numSV)))
# for k in range(numSV):
# SigRecon[k, k] = Sigma[k]
# 分析插入的 Sigma 长度
analyse_data(Sigma, 20)
SigRecon = mat(eye(numSV) * Sigma[: numSV])
reconMat = U[:, :numSV] * SigRecon * VT[:numSV, :]
print "****reconstructed matrix using %d singular values *****" % numSV
printMat(reconMat, thresh)
```
[完整代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/14.SVD/svdRecommend.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/14.SVD/svdRecommend.py>
* * *
* **作者: [片刻](http://cwiki.apachecn.org/display/~jiangzhonglian) [1988](http://cwiki.apachecn.org/display/~lihuisong)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**

446
docs/ml/15.大数据与MapReduce.md → docs/ml/15.md
View File

@@ -1,223 +1,223 @@
# 第15章 大数据与MapReduce
![大数据与MapReduce首页](http://data.apachecn.org/img/AiLearning/ml/15.BigData_MapReduce/mr_headPage.jpg "大数据与MapReduce首页")
## 大数据 概述
`大数据: 收集到的数据已经远远超出了我们的处理能力。`
## 大数据 场景
```
假如你为一家网络购物商店工作，很多用户访问该网站，其中有些人会购买商品，有些人则随意浏览后就离开。
对于你来说，可能很想识别那些有购物意愿的用户。
那么问题就来了，数据集可能会非常大，在单机上训练要运行好几天。
接下来: 我们讲讲 MapRedece 如何来解决这样的问题
```
## MapRedece
### Hadoop 概述
```
Hadoop 是 MapRedece 框架的一个免费开源实现。
MapReduce: 分布式的计算框架，可以将单个计算作业分配给多台计算机执行。
```
### MapRedece 原理
> MapRedece 工作原理
* 主节点控制 MapReduce 的作业流程
* MapReduce 的作业可以分成map任务和reduce任务
* map 任务之间不做数据交流，reduce 任务也一样
* 在 map 和 reduce 阶段中间，有一个 sort 和 combine 阶段
* 数据被重复存放在不同的机器上，以防止某个机器失效
* mapper 和 reducer 传输的数据形式为 key/value对
![MapReduce框架的示意图](http://data.apachecn.org/img/AiLearning/ml/15.BigData_MapReduce/mr_1_cluster.jpg "MapReduce框架的示意图")
> MapRedece 特点
```
优点: 使程序以并行的方式执行，可在短时间内完成大量工作。
缺点: 算法必须经过重写，需要对系统工程有一定的理解。
适用数据类型: 数值型和标称型数据。
```
### Hadoop 流(Python 调用)
> 理论简介
例如: Hadoop流可以像Linux命令一样执行
```Shell
cat inputFile.txt | python mapper.py | sort | python reducer.py > outputFile.txt
```
类似的Hadoop流就可以在多台机器上分布式执行，用户可以通过Linux命令来测试Python语言编写的MapReduce脚本。
> 实战脚本
```
# 测试 Mapper
# Linux
cat data/15.BigData_MapReduce/inputFile.txt | python src/python/15.BigData_MapReduce/mrMeanMapper.py
# Window
# python src/python/15.BigData_MapReduce/mrMeanMapper.py < data/15.BigData_MapReduce/inputFile.txt
# 测试 Reducer
# Linux
cat data/15.BigData_MapReduce/inputFile.txt | python src/python/15.BigData_MapReduce/mrMeanMapper.py | python src/python/15.BigData_MapReduce/mrMeanReducer.py
# Window
# python src/python/15.BigData_MapReduce/mrMeanMapper.py < data/15.BigData_MapReduce/inputFile.txt | python src/python/15.BigData_MapReduce/mrMeanReducer.py
```
### MapReduce 机器学习
#### Mahout in Action
1. 简单贝叶斯: 它属于为数不多的可以很自然的使用MapReduce的算法。通过统计在某个类别下某特征的概率。
2. k-近邻算法: 高维数据下（如文本、图像和视频）流行的近邻查找方法是局部敏感哈希算法。
3. 支持向量机(SVM): 使用随机梯度下降算法求解，如Pegasos算法。
4. 奇异值分解: Lanczos算法是一个有效的求解近似特征值的算法。
5. k-均值聚类: canopy算法初始化k个簇，然后再运行K-均值求解结果。
### 使用 mrjob 库将 MapReduce 自动化
> 理论简介
* MapReduce 作业流自动化的框架: Cascading 和 Oozie.
* mrjob 是一个不错的学习工具，与2010年底实现了开源，来之于 Yelp(一个餐厅点评网站).
```Shell
python src/python/15.BigData_MapReduce/mrMean.py < data/15.BigData_MapReduce/inputFile.txt > data/15.BigData_MapReduce/myOut.txt
```
> 实战脚本
```
# 测试 mrjob的案例
# 先测试一下mapper方法
# python src/python/15.BigData_MapReduce/mrMean.py --mapper < data/15.BigData_MapReduce/inputFile.txt
# 运行整个程序，移除 --mapper 就行
python src/python/15.BigData_MapReduce/mrMean.py < data/15.BigData_MapReduce/inputFile.txt
```
### 项目案例: 分布式 SVM 的 Pegasos 算法
Pegasos是指原始估计梯度求解器(Peimal Estimated sub-GrAdient Solver)
#### Pegasos 工作原理
1. 从训练集中随机挑选一些样本点添加到待处理列表中
2. 按序判断每个样本点是否被正确分类
* 如果是则忽略
* 如果不是则将其加入到待更新集合。
3. 批处理完毕后，权重向量按照这些错分的样本进行更新。
上述算法伪代码如下:
```
将 回归系数w 初始化为0
对每次批处理
随机选择 k 个样本点(向量)
对每个向量
如果该向量被错分:
更新权重向量 w
累加对 w 的更新
```
#### 开发流程
```
收集数据: 数据按文本格式存放。
准备数据: 输入数据已经是可用的格式，所以不需任何准备工作。如果你需要解析一个大规模的数据集，建议使用 map 作业来完成，从而达到并行处理的目的。
分析数据: 无。
训练算法: 与普通的 SVM 一样，在分类器训练上仍需花费大量的时间。
测试算法: 在二维空间上可视化之后，观察超平面，判断算法是否有效。
使用算法: 本例不会展示一个完整的应用，但会展示如何在大数据集上训练SVM。该算法其中一个应用场景就是本文分类，通常在文本分类里可能有大量的文档和成千上万的特征。
```
> 收集数据
文本文件数据格式如下:
```python
0.365032 2.465645 -1
-2.494175 -0.292380 -1
-3.039364 -0.123108 -1
1.348150 0.255696 1
2.768494 1.234954 1
1.232328 -0.601198 1
```
> 准备数据
```python
def loadDataSet(fileName):
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
# dataMat.append([float(lineArr[0]), float(lineArr[1]), float(lineArr[2])])
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
```
> 分析数据: 无
> 训练算法
```python
def batchPegasos(dataSet, labels, lam, T, k):
"""batchPegasos()
Args:
dataMat 特征集合
labels 分类结果集合
lam 固定值
T 迭代次数
k 待处理列表大小
Returns:
w 回归系数
"""
m, n = shape(dataSet)
w = zeros(n) # 回归系数
dataIndex = range(m)
for t in range(1, T+1):
wDelta = mat(zeros(n)) # 重置 wDelta
# 它是学习率，代表了权重调整幅度的大小。（也可以理解为随机梯度的步长，使它不断减小，便于拟合）
# 输入T和K分别设定了迭代次数和待处理列表的大小。在T次迭代过程中，每次需要重新计算eta
eta = 1.0/(lam*t)
random.shuffle(dataIndex)
for j in range(k): # 全部的训练集 内循环中执行批处理，将分类错误的值全部做累加后更新权重向量
i = dataIndex[j]
p = predict(w, dataSet[i, :]) # mapper 代码
# 如果预测正确，并且预测结果的绝对值>=1，因为最大间隔为1, 认为没问题。
# 否则算是预测错误, 通过预测错误的结果，来累计更新w.
if labels[i]*p < 1: # mapper 代码
wDelta += labels[i]*dataSet[i, :].A # 累积变化
# w通过不断的随机梯度的方式来优化
w = (1.0 - 1/t)*w + (eta/k)*wDelta # 在每个 T上应用更改
# print '-----', w
# print '++++++', w
return w
```
[完整代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/15.BigData_MapReduce/pegasos.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/15.BigData_MapReduce/pegasos.py>
运行方式: `python /opt/git/MachineLearning/src/python/15.BigData_MapReduce/mrSVM.py < data/15.BigData_MapReduce/inputFile.txt`
[MR版本的代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/15.BigData_MapReduce/mrSVM.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/15.BigData_MapReduce/mrSVM.py>
* * *
* **作者: [片刻](http://cwiki.apachecn.org/display/~jiangzhonglian) [小瑶](http://cwiki.apachecn.org/display/~chenyao)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**
# 第15章 大数据与MapReduce
![大数据与MapReduce首页](http://data.apachecn.org/img/AiLearning/ml/15.BigData_MapReduce/mr_headPage.jpg "大数据与MapReduce首页")
## 大数据 概述
`大数据: 收集到的数据已经远远超出了我们的处理能力。`
## 大数据 场景
```
假如你为一家网络购物商店工作，很多用户访问该网站，其中有些人会购买商品，有些人则随意浏览后就离开。
对于你来说，可能很想识别那些有购物意愿的用户。
那么问题就来了，数据集可能会非常大，在单机上训练要运行好几天。
接下来: 我们讲讲 MapRedece 如何来解决这样的问题
```
## MapRedece
### Hadoop 概述
```
Hadoop 是 MapRedece 框架的一个免费开源实现。
MapReduce: 分布式的计算框架，可以将单个计算作业分配给多台计算机执行。
```
### MapRedece 原理
> MapRedece 工作原理
* 主节点控制 MapReduce 的作业流程
* MapReduce 的作业可以分成map任务和reduce任务
* map 任务之间不做数据交流，reduce 任务也一样
* 在 map 和 reduce 阶段中间，有一个 sort 和 combine 阶段
* 数据被重复存放在不同的机器上，以防止某个机器失效
* mapper 和 reducer 传输的数据形式为 key/value对
![MapReduce框架的示意图](http://data.apachecn.org/img/AiLearning/ml/15.BigData_MapReduce/mr_1_cluster.jpg "MapReduce框架的示意图")
> MapRedece 特点
```
优点: 使程序以并行的方式执行，可在短时间内完成大量工作。
缺点: 算法必须经过重写，需要对系统工程有一定的理解。
适用数据类型: 数值型和标称型数据。
```
### Hadoop 流(Python 调用)
> 理论简介
例如: Hadoop流可以像Linux命令一样执行
```Shell
cat inputFile.txt | python mapper.py | sort | python reducer.py > outputFile.txt
```
类似的Hadoop流就可以在多台机器上分布式执行，用户可以通过Linux命令来测试Python语言编写的MapReduce脚本。
> 实战脚本
```
# 测试 Mapper
# Linux
cat data/15.BigData_MapReduce/inputFile.txt | python src/python/15.BigData_MapReduce/mrMeanMapper.py
# Window
# python src/python/15.BigData_MapReduce/mrMeanMapper.py < data/15.BigData_MapReduce/inputFile.txt
# 测试 Reducer
# Linux
cat data/15.BigData_MapReduce/inputFile.txt | python src/python/15.BigData_MapReduce/mrMeanMapper.py | python src/python/15.BigData_MapReduce/mrMeanReducer.py
# Window
# python src/python/15.BigData_MapReduce/mrMeanMapper.py < data/15.BigData_MapReduce/inputFile.txt | python src/python/15.BigData_MapReduce/mrMeanReducer.py
```
### MapReduce 机器学习
#### Mahout in Action
1. 简单贝叶斯: 它属于为数不多的可以很自然的使用MapReduce的算法。通过统计在某个类别下某特征的概率。
2. k-近邻算法: 高维数据下（如文本、图像和视频）流行的近邻查找方法是局部敏感哈希算法。
3. 支持向量机(SVM): 使用随机梯度下降算法求解，如Pegasos算法。
4. 奇异值分解: Lanczos算法是一个有效的求解近似特征值的算法。
5. k-均值聚类: canopy算法初始化k个簇，然后再运行K-均值求解结果。
### 使用 mrjob 库将 MapReduce 自动化
> 理论简介
* MapReduce 作业流自动化的框架: Cascading 和 Oozie.
* mrjob 是一个不错的学习工具，与2010年底实现了开源，来之于 Yelp(一个餐厅点评网站).
```Shell
python src/python/15.BigData_MapReduce/mrMean.py < data/15.BigData_MapReduce/inputFile.txt > data/15.BigData_MapReduce/myOut.txt
```
> 实战脚本
```
# 测试 mrjob的案例
# 先测试一下mapper方法
# python src/python/15.BigData_MapReduce/mrMean.py --mapper < data/15.BigData_MapReduce/inputFile.txt
# 运行整个程序，移除 --mapper 就行
python src/python/15.BigData_MapReduce/mrMean.py < data/15.BigData_MapReduce/inputFile.txt
```
### 项目案例: 分布式 SVM 的 Pegasos 算法
Pegasos是指原始估计梯度求解器(Peimal Estimated sub-GrAdient Solver)
#### Pegasos 工作原理
1. 从训练集中随机挑选一些样本点添加到待处理列表中
2. 按序判断每个样本点是否被正确分类
* 如果是则忽略
* 如果不是则将其加入到待更新集合。
3. 批处理完毕后，权重向量按照这些错分的样本进行更新。
上述算法伪代码如下:
```
将 回归系数w 初始化为0
对每次批处理
随机选择 k 个样本点(向量)
对每个向量
如果该向量被错分:
更新权重向量 w
累加对 w 的更新
```
#### 开发流程
```
收集数据: 数据按文本格式存放。
准备数据: 输入数据已经是可用的格式，所以不需任何准备工作。如果你需要解析一个大规模的数据集，建议使用 map 作业来完成，从而达到并行处理的目的。
分析数据: 无。
训练算法: 与普通的 SVM 一样，在分类器训练上仍需花费大量的时间。
测试算法: 在二维空间上可视化之后，观察超平面，判断算法是否有效。
使用算法: 本例不会展示一个完整的应用，但会展示如何在大数据集上训练SVM。该算法其中一个应用场景就是本文分类，通常在文本分类里可能有大量的文档和成千上万的特征。
```
> 收集数据
文本文件数据格式如下:
```python
0.365032 2.465645 -1
-2.494175 -0.292380 -1
-3.039364 -0.123108 -1
1.348150 0.255696 1
2.768494 1.234954 1
1.232328 -0.601198 1
```
> 准备数据
```python
def loadDataSet(fileName):
dataMat = []
labelMat = []
fr = open(fileName)
for line in fr.readlines():
lineArr = line.strip().split('\t')
# dataMat.append([float(lineArr[0]), float(lineArr[1]), float(lineArr[2])])
dataMat.append([float(lineArr[0]), float(lineArr[1])])
labelMat.append(float(lineArr[2]))
return dataMat, labelMat
```
> 分析数据: 无
> 训练算法
```python
def batchPegasos(dataSet, labels, lam, T, k):
"""batchPegasos()
Args:
dataMat 特征集合
labels 分类结果集合
lam 固定值
T 迭代次数
k 待处理列表大小
Returns:
w 回归系数
"""
m, n = shape(dataSet)
w = zeros(n) # 回归系数
dataIndex = range(m)
for t in range(1, T+1):
wDelta = mat(zeros(n)) # 重置 wDelta
# 它是学习率，代表了权重调整幅度的大小。（也可以理解为随机梯度的步长，使它不断减小，便于拟合）
# 输入T和K分别设定了迭代次数和待处理列表的大小。在T次迭代过程中，每次需要重新计算eta
eta = 1.0/(lam*t)
random.shuffle(dataIndex)
for j in range(k): # 全部的训练集 内循环中执行批处理，将分类错误的值全部做累加后更新权重向量
i = dataIndex[j]
p = predict(w, dataSet[i, :]) # mapper 代码
# 如果预测正确，并且预测结果的绝对值>=1，因为最大间隔为1, 认为没问题。
# 否则算是预测错误, 通过预测错误的结果，来累计更新w.
if labels[i]*p < 1: # mapper 代码
wDelta += labels[i]*dataSet[i, :].A # 累积变化
# w通过不断的随机梯度的方式来优化
w = (1.0 - 1/t)*w + (eta/k)*wDelta # 在每个 T上应用更改
# print '-----', w
# print '++++++', w
return w
```
[完整代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/15.BigData_MapReduce/pegasos.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/15.BigData_MapReduce/pegasos.py>
运行方式: `python /opt/git/MachineLearning/src/python/15.BigData_MapReduce/mrSVM.py < data/15.BigData_MapReduce/inputFile.txt`
[MR版本的代码地址](https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/15.BigData_MapReduce/mrSVM.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/15.BigData_MapReduce/mrSVM.py>
* * *
* **作者: [片刻](http://cwiki.apachecn.org/display/~jiangzhonglian) [小瑶](http://cwiki.apachecn.org/display/~chenyao)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**

172
docs/ml/16.推荐系统.md → docs/ml/16.md
View File

@@ -1,86 +1,86 @@
# 第16章 推荐系统
## 背景与挖掘目标
随着互联网的快速发展，用户很难快速从海量信息中寻找到自己感兴趣的信息。因此诞生了: 搜索引擎+推荐系统
本章节-推荐系统:
1. 帮助用户发现其感兴趣和可能感兴趣的信息。
2. 让网站价值信息脱颖而出，得到广大用户的认可。
3. 提高用户对网站的忠诚度和关注度，建立稳固用户群体。
## 分析方法与过程
本案例的目标是对用户进行推荐，即以一定的方式将用户与物品（本次指网页）之间建立联系。
由于用户访问网站的数据记录很多，如果不对数据进行分类处理，对所有的记录直接采用推荐系统进行推荐，这样会存在一下问题。
1. 数据量太大意味着物品数与用户数很多，在模型构建用户与物品稀疏矩阵时，出现设备内存空间不够的情况，并且模型计算需要消耗大量的时间。
2. 用户区别很大，不同的用户关注的信息不一样，因此，即使能够得到推荐结果，其效果也会不好。
为了避免出现上述问题，需要进行分类处理与分析。
正常的情况下，需要对用户的兴趣爱好以及需求进行分类。
因为在用户访问记录中，没有记录用户访问页面时间的长短，因此不容易判断用户兴趣爱好。
因此，本文根据用户浏览的网页信息进行分析处理，主要采用以下方法处理: 以用户浏览网页的类型进行分类，然后对每个类型中的内容进行推荐。
分析过程如下:
* 从系统中获取用户访问网站的原始记录。
* 对数据进行多维分析，包括用户访问内容，流失用户分析以及用户分类等分析。
* 对数据进行预处理，包含数据去重、数据变换和数据分类鞥处理过程。
* 以用户访问html后缀的页面为关键条件，对数据进行处理。
* 对比多种推荐算法进行推荐，通过模型评价，得到比较好的智能推荐模型。通过模型对样本数据进行预测，获得推荐结果。
## 主流推荐算法
| 推荐方法 | 描述 |
| --- | --- |
| 基于内容推荐 | |
| 协同过滤推荐 | |
| 基于规则推荐 | |
| 基于效用推荐 | |
| 基于知识推荐 | |
| 组合推荐 | |
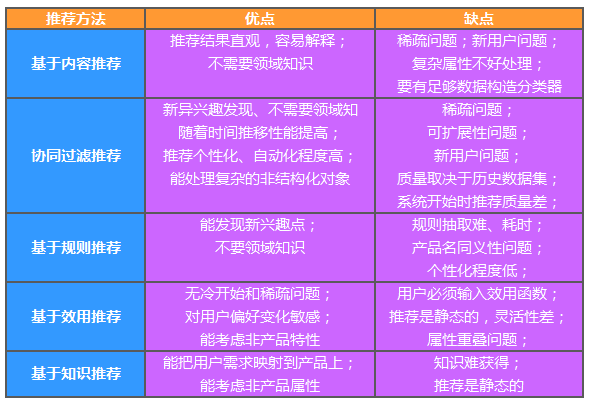
![推荐方法对比](http://data.apachecn.org/img/AiLearning/ml/16.RecommendedSystem/推荐方法对比.png)
### 基于知识推荐
基于知识的推荐（Knowledge-based Recommendation）在某种程度是可以看成是一种推理（Inference）技术，它不是建立在用户需要和偏好基础上推荐的。基于知识的方法因它们所用的功能知识不同而有明显区别。效用知识（Functional Knowledge）是一种关于一个项目如何满足某一特定用户的知识，因此能解释需要和推荐的关系，所以用户资料可以是任何能支持推理的知识结构，它可以是用户已经规范化的查询，也可以是一个更详细的用户需要的表示。
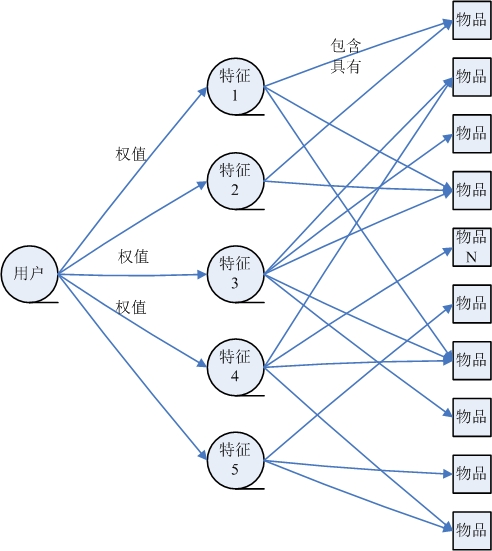
![基于知识的推荐](http://data.apachecn.org/img/AiLearning/ml/16.RecommendedSystem/基于知识的推荐.jpg)
### 协同过滤推荐
* memory-based推荐
* Item-based方法
* User-based方法
* Memory-based推荐方法通过执行最近邻搜索，把每一个Item或者User看成一个向量，计算其他所有Item或者User与它的相似度。有了Item或者User之间的两两相似度之后，就可以进行预测与推荐了。
* model-based推荐
* Model-based推荐最常见的方法为Matrix factorization.
* 矩阵分解通过把原始的评分矩阵R分解为两个矩阵相乘，并且只考虑有评分的值，训练时不考虑missing项的值。R矩阵分解成为U与V两个矩阵后，评分矩阵R中missing的值就可以通过U矩阵中的某列和V矩阵的某行相乘得到
* 矩阵分解的目标函数: U矩阵与V矩阵的可以通过梯度下降(gradient descent)算法求得，通过交替更新u与v多次迭代收敛之后可求出U与V。
* 矩阵分解背后的核心思想，找到两个矩阵，它们相乘之后得到的那个矩阵的值，与评分矩阵R中有值的位置中的值尽可能接近。这样一来，分解出来的两个矩阵相乘就尽可能还原了评分矩阵R，因为有值的地方，值都相差得尽可能地小，那么missing的值通过这样的方式计算得到，比较符合趋势。
* 协同过滤中主要存在如下两个问题: 稀疏性与冷启动问题。已有的方案通常会通过引入多个不同的数据源或者辅助信息(Side information)来解决这些问题，用户的Side information可以是用户的基本个人信息、用户画像信息等，而Item的Side information可以是物品的content信息等。
## 效果评估
1. 召回率和准确率 【人为统计分析】
2. F值(P-R曲线) 【偏重: 非均衡问题】
3. ROC和AUC 【偏重: 不同结果的对比】
* * *
* **作者: [片刻](https://github.com/jiangzhonglian)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**
> 摘录的原文地址:
* [推荐系统中常用算法 以及优点缺点对比](http://www.36dsj.com/archives/9519)
* [推荐算法的基于知识推荐](https://zhidao.baidu.com/question/2013524494179442228.html)
* [推荐系统中基于深度学习的混合协同过滤模型](http://www.iteye.com/news/32100)
# 第16章 推荐系统
## 背景与挖掘目标
随着互联网的快速发展，用户很难快速从海量信息中寻找到自己感兴趣的信息。因此诞生了: 搜索引擎+推荐系统
本章节-推荐系统:
1. 帮助用户发现其感兴趣和可能感兴趣的信息。
2. 让网站价值信息脱颖而出，得到广大用户的认可。
3. 提高用户对网站的忠诚度和关注度，建立稳固用户群体。
## 分析方法与过程
本案例的目标是对用户进行推荐，即以一定的方式将用户与物品（本次指网页）之间建立联系。
由于用户访问网站的数据记录很多，如果不对数据进行分类处理，对所有的记录直接采用推荐系统进行推荐，这样会存在一下问题。
1. 数据量太大意味着物品数与用户数很多，在模型构建用户与物品稀疏矩阵时，出现设备内存空间不够的情况，并且模型计算需要消耗大量的时间。
2. 用户区别很大，不同的用户关注的信息不一样，因此，即使能够得到推荐结果，其效果也会不好。
为了避免出现上述问题，需要进行分类处理与分析。
正常的情况下，需要对用户的兴趣爱好以及需求进行分类。
因为在用户访问记录中，没有记录用户访问页面时间的长短，因此不容易判断用户兴趣爱好。
因此，本文根据用户浏览的网页信息进行分析处理，主要采用以下方法处理: 以用户浏览网页的类型进行分类，然后对每个类型中的内容进行推荐。
分析过程如下:
* 从系统中获取用户访问网站的原始记录。
* 对数据进行多维分析，包括用户访问内容，流失用户分析以及用户分类等分析。
* 对数据进行预处理，包含数据去重、数据变换和数据分类鞥处理过程。
* 以用户访问html后缀的页面为关键条件，对数据进行处理。
* 对比多种推荐算法进行推荐，通过模型评价，得到比较好的智能推荐模型。通过模型对样本数据进行预测，获得推荐结果。
## 主流推荐算法
| 推荐方法 | 描述 |
| --- | --- |
| 基于内容推荐 | |
| 协同过滤推荐 | |
| 基于规则推荐 | |
| 基于效用推荐 | |
| 基于知识推荐 | |
| 组合推荐 | |
![推荐方法对比](http://data.apachecn.org/img/AiLearning/ml/16.RecommendedSystem/推荐方法对比.png)
### 基于知识推荐
基于知识的推荐（Knowledge-based Recommendation）在某种程度是可以看成是一种推理（Inference）技术，它不是建立在用户需要和偏好基础上推荐的。基于知识的方法因它们所用的功能知识不同而有明显区别。效用知识（Functional Knowledge）是一种关于一个项目如何满足某一特定用户的知识，因此能解释需要和推荐的关系，所以用户资料可以是任何能支持推理的知识结构，它可以是用户已经规范化的查询，也可以是一个更详细的用户需要的表示。
![基于知识的推荐](http://data.apachecn.org/img/AiLearning/ml/16.RecommendedSystem/基于知识的推荐.jpg)
### 协同过滤推荐
* memory-based推荐
* Item-based方法
* User-based方法
* Memory-based推荐方法通过执行最近邻搜索，把每一个Item或者User看成一个向量，计算其他所有Item或者User与它的相似度。有了Item或者User之间的两两相似度之后，就可以进行预测与推荐了。
* model-based推荐
* Model-based推荐最常见的方法为Matrix factorization.
* 矩阵分解通过把原始的评分矩阵R分解为两个矩阵相乘，并且只考虑有评分的值，训练时不考虑missing项的值。R矩阵分解成为U与V两个矩阵后，评分矩阵R中missing的值就可以通过U矩阵中的某列和V矩阵的某行相乘得到
* 矩阵分解的目标函数: U矩阵与V矩阵的可以通过梯度下降(gradient descent)算法求得，通过交替更新u与v多次迭代收敛之后可求出U与V。
* 矩阵分解背后的核心思想，找到两个矩阵，它们相乘之后得到的那个矩阵的值，与评分矩阵R中有值的位置中的值尽可能接近。这样一来，分解出来的两个矩阵相乘就尽可能还原了评分矩阵R，因为有值的地方，值都相差得尽可能地小，那么missing的值通过这样的方式计算得到，比较符合趋势。
* 协同过滤中主要存在如下两个问题: 稀疏性与冷启动问题。已有的方案通常会通过引入多个不同的数据源或者辅助信息(Side information)来解决这些问题，用户的Side information可以是用户的基本个人信息、用户画像信息等，而Item的Side information可以是物品的content信息等。
## 效果评估
1. 召回率和准确率 【人为统计分析】
2. F值(P-R曲线) 【偏重: 非均衡问题】
3. ROC和AUC 【偏重: 不同结果的对比】
* * *
* **作者: [片刻](https://github.com/jiangzhonglian)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**
> 摘录的原文地址:
* [推荐系统中常用算法 以及优点缺点对比](http://www.36dsj.com/archives/9519)
* [推荐算法的基于知识推荐](https://zhidao.baidu.com/question/2013524494179442228.html)
* [推荐系统中基于深度学习的混合协同过滤模型](http://www.iteye.com/news/32100)

1134
docs/ml/2.k-近邻算法.md → docs/ml/2.md
View File

File diff suppressed because it is too large Load Diff

834
docs/ml/3.决策树.md → docs/ml/3.md
View File

@@ -1,417 +1,417 @@
# 第3章 决策树
<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=default"></script>
![决策树_首页](http://data.apachecn.org/img/AiLearning/ml/3.DecisionTree/DecisionTree_headPage_xy.png "决策树首页")
## 决策树 概述
`决策树（Decision Tree）算法是一种基本的分类与回归方法，是最经常使用的数据挖掘算法之一。我们这章节只讨论用于分类的决策树。`
`决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是 if-then 规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。`
`决策树学习通常包括 3 个步骤: 特征选择、决策树的生成和决策树的修剪。`
## 决策树 场景
一个叫做 "二十个问题" 的游戏，游戏的规则很简单: 参与游戏的一方在脑海中想某个事物，其他参与者向他提问，只允许提 20 个问题，问题的答案也只能用对或错回答。问问题的人通过推断分解，逐步缩小待猜测事物的范围，最后得到游戏的答案。
一个邮件分类系统，大致工作流程如下:
![决策树-流程图](http://data.apachecn.org/img/AiLearning/ml/3.DecisionTree/决策树-流程图.jpg "决策树示例流程图")
```
首先检测发送邮件域名地址。如果地址为 myEmployer.com, 则将其放在分类 "无聊时需要阅读的邮件"中。
如果邮件不是来自这个域名，则检测邮件内容里是否包含单词 "曲棍球" , 如果包含则将邮件归类到 "需要及时处理的朋友邮件",
如果不包含则将邮件归类到 "无需阅读的垃圾邮件" 。
```
决策树的定义:
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点（node）和有向边（directed edge）组成。结点有两种类型: 内部结点（internal node）和叶结点（leaf node）。内部结点表示一个特征或属性(features)，叶结点表示一个类(labels)。
用决策树对需要测试的实例进行分类: 从根节点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点；这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分配到叶结点的类中。
## 决策树 原理
### 决策树 须知概念
#### 信息熵 & 信息增益
熵（entropy）:
熵指的是体系的混乱的程度，在不同的学科中也有引申出的更为具体的定义，是各领域十分重要的参量。
信息论（information theory）中的熵（香农熵）:
是一种信息的度量方式，表示信息的混乱程度，也就是说: 信息越有序，信息熵越低。例如: 火柴有序放在火柴盒里，熵值很低，相反，熵值很高。
信息增益（information gain）:
在划分数据集前后信息发生的变化称为信息增益。
### 决策树 工作原理
如何构造一个决策树?<br/>
我们使用 createBranch() 方法，如下所示:
```
def createBranch():
'''
此处运用了迭代的思想。 感兴趣可以搜索 迭代 recursion， 甚至是 dynamic programing。
'''
检测数据集中的所有数据的分类标签是否相同:
If so return 类标签
Else:
寻找划分数据集的最好特征（划分之后信息熵最小，也就是信息增益最大的特征）
划分数据集
创建分支节点
for 每个划分的子集
调用函数 createBranch （创建分支的函数）并增加返回结果到分支节点中
return 分支节点
```
### 决策树 开发流程
```
收集数据: 可以使用任何方法。
准备数据: 树构造算法 (这里使用的是ID3算法，只适用于标称型数据，这就是为什么数值型数据必须离散化。 还有其他的树构造算法，比如CART)
分析数据: 可以使用任何方法，构造树完成之后，我们应该检查图形是否符合预期。
训练算法: 构造树的数据结构。
测试算法: 使用训练好的树计算错误率。
使用算法: 此步骤可以适用于任何监督学习任务，而使用决策树可以更好地理解数据的内在含义。
```
### 决策树 算法特点
```
优点: 计算复杂度不高，输出结果易于理解，数据有缺失也能跑，可以处理不相关特征。
缺点: 容易过拟合。
适用数据类型: 数值型和标称型。
```
## 决策树 项目案例
### 项目案例1: 判定鱼类和非鱼类
#### 项目概述
根据以下 2 个特征，将动物分成两类: 鱼类和非鱼类。
特征:
1. 不浮出水面是否可以生存
2. 是否有脚蹼
#### 开发流程
[完整代码地址](/src/py2.x/ml/3.DecisionTree/DecisionTree.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/3.DecisionTree/DecisionTree.py>
```
收集数据: 可以使用任何方法
准备数据: 树构造算法（这里使用的是ID3算法，因此数值型数据必须离散化。）
分析数据: 可以使用任何方法，构造树完成之后，我们可以将树画出来。
训练算法: 构造树结构
测试算法: 使用习得的决策树执行分类
使用算法: 此步骤可以适用于任何监督学习任务，而使用决策树可以更好地理解数据的内在含义
```
> 收集数据: 可以使用任何方法
![海洋生物数据](http://data.apachecn.org/img/AiLearning/ml/3.DecisionTree/DT_海洋生物数据.png)
我们利用 createDataSet() 函数输入数据
```python
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers']
return dataSet, labels
```
> 准备数据: 树构造算法
此处，由于我们输入的数据本身就是离散化数据，所以这一步就省略了。
> 分析数据: 可以使用任何方法，构造树完成之后，我们可以将树画出来。
![熵的计算公式](http://data.apachecn.org/img/AiLearning/ml/3.DecisionTree/熵的计算公式.jpg)
计算给定数据集的香农熵的函数
```python
def calcShannonEnt(dataSet):
# 求list的长度，表示计算参与训练的数据量
numEntries = len(dataSet)
# 计算分类标签label出现的次数
labelCounts = {}
# the the number of unique elements and their occurrence
for featVec in dataSet:
# 将当前实例的标签存储，即每一行数据的最后一个数据代表的是标签
currentLabel = featVec[-1]
# 为所有可能的分类创建字典，如果当前的键值不存在，则扩展字典并将当前键值加入字典。每个键值都记录了当前类别出现的次数。
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
# 对于 label 标签的占比，求出 label 标签的香农熵
shannonEnt = 0.0
for key in labelCounts:
# 使用所有类标签的发生频率计算类别出现的概率。
prob = float(labelCounts[key])/numEntries
# 计算香农熵，以 2 为底求对数
shannonEnt -= prob * log(prob, 2)
return shannonEnt
```
按照给定特征划分数据集
`将指定特征的特征值等于 value 的行剩下列作为子数据集。`
```python
def splitDataSet(dataSet, index, value):
"""splitDataSet(通过遍历dataSet数据集，求出index对应的colnum列的值为value的行)
就是依据index列进行分类，如果index列的数据等于 value的时候，就要将 index 划分到我们创建的新的数据集中
Args:
dataSet 数据集 待划分的数据集
index 表示每一行的index列 划分数据集的特征
value 表示index列对应的value值 需要返回的特征的值。
Returns:
index列为value的数据集【该数据集需要排除index列】
"""
retDataSet = []
for featVec in dataSet:
# index列为value的数据集【该数据集需要排除index列】
# 判断index列的值是否为value
if featVec[index] == value:
# chop out index used for splitting
# [:index]表示前index行，即若 index 为2，就是取 featVec 的前 index 行
reducedFeatVec = featVec[:index]
'''
请百度查询一下: extend和append的区别
music_media.append(object) 向列表中添加一个对象object
           music_media.extend(sequence) 把一个序列seq的内容添加到列表中 (跟 += 在list运用类似， music_media += sequence)
           1、使用append的时候，是将object看作一个对象，整体打包添加到music_media对象中。
2、使用extend的时候，是将sequence看作一个序列，将这个序列和music_media序列合并，并放在其后面。
music_media = []
music_media.extend([1,2,3])
print music_media
           #结果:
           #[1, 2, 3]
music_media.append([4,5,6])
print music_media
#结果:
           #[1, 2, 3, [4, 5, 6]]
music_media.extend([7,8,9])
print music_media
#结果:
           #[1, 2, 3, [4, 5, 6], 7, 8, 9]
'''
reducedFeatVec.extend(featVec[index+1:])
# [index+1:]表示从跳过 index 的 index+1行，取接下来的数据
# 收集结果值 index列为value的行【该行需要排除index列】
retDataSet.append(reducedFeatVec)
return retDataSet
```
选择最好的数据集划分方式
```python
def chooseBestFeatureToSplit(dataSet):
"""chooseBestFeatureToSplit(选择最好的特征)
Args:
dataSet 数据集
Returns:
bestFeature 最优的特征列
"""
# 求第一行有多少列的 Feature, 最后一列是label列嘛
numFeatures = len(dataSet[0]) - 1
# 数据集的原始信息熵
baseEntropy = calcShannonEnt(dataSet)
# 最优的信息增益值, 和最优的Featurn编号
bestInfoGain, bestFeature = 0.0, -1
# iterate over all the features
for i in range(numFeatures):
# create a list of all the examples of this feature
# 获取对应的feature下的所有数据
featList = [example[i] for example in dataSet]
# get a set of unique values
# 获取剔重后的集合，使用set对list数据进行去重
uniqueVals = set(featList)
# 创建一个临时的信息熵
newEntropy = 0.0
# 遍历某一列的value集合，计算该列的信息熵
# 遍历当前特征中的所有唯一属性值，对每个唯一属性值划分一次数据集，计算数据集的新熵值，并对所有唯一特征值得到的熵求和。
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
# 计算概率
prob = len(subDataSet)/float(len(dataSet))
# 计算信息熵
newEntropy += prob * calcShannonEnt(subDataSet)
# gain[信息增益]: 划分数据集前后的信息变化， 获取信息熵最大的值
# 信息增益是熵的减少或者是数据无序度的减少。最后，比较所有特征中的信息增益，返回最好特征划分的索引值。
infoGain = baseEntropy - newEntropy
print 'infoGain=', infoGain, 'bestFeature=', i, baseEntropy, newEntropy
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
```
```
问: 上面的 newEntropy 为什么是根据子集计算的呢？
答: 因为我们在根据一个特征计算香农熵的时候，该特征的分类值是相同，这个特征这个分类的香农熵为 0；
这就是为什么计算新的香农熵的时候使用的是子集。
```
> 训练算法: 构造树的数据结构
创建树的函数代码如下:
```python
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
# 如果数据集的最后一列的第一个值出现的次数=整个集合的数量，也就说只有一个类别，就只直接返回结果就行
# 第一个停止条件: 所有的类标签完全相同，则直接返回该类标签。
# count() 函数是统计括号中的值在list中出现的次数
if classList.count(classList[0]) == len(classList):
return classList[0]
# 如果数据集只有1列，那么最初出现label次数最多的一类，作为结果
# 第二个停止条件: 使用完了所有特征，仍然不能将数据集划分成仅包含唯一类别的分组。
if len(dataSet[0]) == 1:
return majorityCnt(classList)
# 选择最优的列，得到最优列对应的label含义
bestFeat = chooseBestFeatureToSplit(dataSet)
# 获取label的名称
bestFeatLabel = labels[bestFeat]
# 初始化myTree
myTree = {bestFeatLabel: {}}
# 注: labels列表是可变对象，在PYTHON函数中作为参数时传址引用，能够被全局修改
# 所以这行代码导致函数外的同名变量被删除了元素，造成例句无法执行，提示'no surfacing' is not in list
del(labels[bestFeat])
# 取出最优列，然后它的branch做分类
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
# 求出剩余的标签label
subLabels = labels[:]
# 遍历当前选择特征包含的所有属性值，在每个数据集划分上递归调用函数createTree()
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
# print 'myTree', value, myTree
return myTree
```
> 测试算法: 使用决策树执行分类
```python
def classify(inputTree, featLabels, testVec):
"""classify(给输入的节点，进行分类)
Args:
inputTree 决策树模型
featLabels Feature标签对应的名称
testVec 测试输入的数据
Returns:
classLabel 分类的结果值，需要映射label才能知道名称
"""
# 获取tree的根节点对于的key值
firstStr = list(inputTree.keys())[0]
# 通过key得到根节点对应的value
secondDict = inputTree[firstStr]
# 判断根节点名称获取根节点在label中的先后顺序，这样就知道输入的testVec怎么开始对照树来做分类
featIndex = featLabels.index(firstStr)
# 测试数据，找到根节点对应的label位置，也就知道从输入的数据的第几位来开始分类
key = testVec[featIndex]
valueOfFeat = secondDict[key]
print '+++', firstStr, 'xxx', secondDict, '---', key, '>>>', valueOfFeat
# 判断分枝是否结束: 判断valueOfFeat是否是dict类型
if isinstance(valueOfFeat, dict):
classLabel = classify(valueOfFeat, featLabels, testVec)
else:
classLabel = valueOfFeat
return classLabel
```
> 使用算法: 此步骤可以适用于任何监督学习任务，而使用决策树可以更好地理解数据的内在含义。
### 项目案例2: 使用决策树预测隐形眼镜类型
[完整代码地址](/src/py2.x/ml/3.DecisionTree/DecisionTree.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/3.DecisionTree/DecisionTree.py>
#### 项目概述
隐形眼镜类型包括硬材质、软材质以及不适合佩戴隐形眼镜。我们需要使用决策树预测患者需要佩戴的隐形眼镜类型。
#### 开发流程
1. 收集数据: 提供的文本文件。
2. 解析数据: 解析 tab 键分隔的数据行
3. 分析数据: 快速检查数据，确保正确地解析数据内容，使用 createPlot() 函数绘制最终的树形图。
4. 训练算法: 使用 createTree() 函数。
5. 测试算法: 编写测试函数验证决策树可以正确分类给定的数据实例。
6. 使用算法: 存储树的数据结构，以便下次使用时无需重新构造树。
> 收集数据: 提供的文本文件
文本文件数据格式如下:
```
young myope no reduced no lenses
pre myope no reduced no lenses
presbyopic myope no reduced no lenses
```
> 解析数据: 解析 tab 键分隔的数据行
```python
lecses = [inst.strip().split('\t') for inst in fr.readlines()]
lensesLabels = ['age', 'prescript', 'astigmatic', 'tearRate']
```
> 分析数据: 快速检查数据，确保正确地解析数据内容，使用 createPlot() 函数绘制最终的树形图。
```python
>>> treePlotter.createPlot(lensesTree)
```
> 训练算法: 使用 createTree() 函数
```python
>>> lensesTree = trees.createTree(lenses, lensesLabels)
>>> lensesTree
{'tearRate': {'reduced': 'no lenses', 'normal': {'astigmatic':{'yes':
{'prescript':{'hyper':{'age':{'pre':'no lenses', 'presbyopic':
'no lenses', 'young':'hard'}}, 'myope':'hard'}}, 'no':{'age':{'pre':
'soft', 'presbyopic':{'prescript': {'hyper':'soft', 'myope':
'no lenses'}}, 'young':'soft'}}}}}
```
> 测试算法: 编写测试函数验证决策树可以正确分类给定的数据实例。
> 使用算法: 存储树的数据结构，以便下次使用时无需重新构造树。
使用 pickle 模块存储决策树
```python
def storeTree(inputTree, filename):
import pickle
fw = open(filename, 'wb')
pickle.dump(inputTree, fw)
fw.close()
def grabTree(filename):
import pickle
fr = open(filename, 'rb')
return pickle.load(fr)
```
* * *
* **作者: [片刻](https://github.com/jiangzhonglian) [小瑶](http://cwiki.apachecn.org/display/~chenyao)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**
# 第3章 决策树
<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=default"></script>
![决策树_首页](http://data.apachecn.org/img/AiLearning/ml/3.DecisionTree/DecisionTree_headPage_xy.png "决策树首页")
## 决策树 概述
`决策树（Decision Tree）算法是一种基本的分类与回归方法，是最经常使用的数据挖掘算法之一。我们这章节只讨论用于分类的决策树。`
`决策树模型呈树形结构，在分类问题中，表示基于特征对实例进行分类的过程。它可以认为是 if-then 规则的集合，也可以认为是定义在特征空间与类空间上的条件概率分布。`
`决策树学习通常包括 3 个步骤: 特征选择、决策树的生成和决策树的修剪。`
## 决策树 场景
一个叫做 "二十个问题" 的游戏，游戏的规则很简单: 参与游戏的一方在脑海中想某个事物，其他参与者向他提问，只允许提 20 个问题，问题的答案也只能用对或错回答。问问题的人通过推断分解，逐步缩小待猜测事物的范围，最后得到游戏的答案。
一个邮件分类系统，大致工作流程如下:
![决策树-流程图](http://data.apachecn.org/img/AiLearning/ml/3.DecisionTree/决策树-流程图.jpg "决策树示例流程图")
```
首先检测发送邮件域名地址。如果地址为 myEmployer.com, 则将其放在分类 "无聊时需要阅读的邮件"中。
如果邮件不是来自这个域名，则检测邮件内容里是否包含单词 "曲棍球" , 如果包含则将邮件归类到 "需要及时处理的朋友邮件",
如果不包含则将邮件归类到 "无需阅读的垃圾邮件" 。
```
决策树的定义:
分类决策树模型是一种描述对实例进行分类的树形结构。决策树由结点（node）和有向边（directed edge）组成。结点有两种类型: 内部结点（internal node）和叶结点（leaf node）。内部结点表示一个特征或属性(features)，叶结点表示一个类(labels)。
用决策树对需要测试的实例进行分类: 从根节点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点；这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分配到叶结点的类中。
## 决策树 原理
### 决策树 须知概念
#### 信息熵 & 信息增益
熵（entropy）:
熵指的是体系的混乱的程度，在不同的学科中也有引申出的更为具体的定义，是各领域十分重要的参量。
信息论（information theory）中的熵（香农熵）:
是一种信息的度量方式，表示信息的混乱程度，也就是说: 信息越有序，信息熵越低。例如: 火柴有序放在火柴盒里，熵值很低，相反，熵值很高。
信息增益（information gain）:
在划分数据集前后信息发生的变化称为信息增益。
### 决策树 工作原理
如何构造一个决策树?<br/>
我们使用 createBranch() 方法，如下所示:
```
def createBranch():
'''
此处运用了迭代的思想。 感兴趣可以搜索 迭代 recursion， 甚至是 dynamic programing。
'''
检测数据集中的所有数据的分类标签是否相同:
If so return 类标签
Else:
寻找划分数据集的最好特征（划分之后信息熵最小，也就是信息增益最大的特征）
划分数据集
创建分支节点
for 每个划分的子集
调用函数 createBranch （创建分支的函数）并增加返回结果到分支节点中
return 分支节点
```
### 决策树 开发流程
```
收集数据: 可以使用任何方法。
准备数据: 树构造算法 (这里使用的是ID3算法，只适用于标称型数据，这就是为什么数值型数据必须离散化。 还有其他的树构造算法，比如CART)
分析数据: 可以使用任何方法，构造树完成之后，我们应该检查图形是否符合预期。
训练算法: 构造树的数据结构。
测试算法: 使用训练好的树计算错误率。
使用算法: 此步骤可以适用于任何监督学习任务，而使用决策树可以更好地理解数据的内在含义。
```
### 决策树 算法特点
```
优点: 计算复杂度不高，输出结果易于理解，数据有缺失也能跑，可以处理不相关特征。
缺点: 容易过拟合。
适用数据类型: 数值型和标称型。
```
## 决策树 项目案例
### 项目案例1: 判定鱼类和非鱼类
#### 项目概述
根据以下 2 个特征，将动物分成两类: 鱼类和非鱼类。
特征:
1. 不浮出水面是否可以生存
2. 是否有脚蹼
#### 开发流程
[完整代码地址](/src/py2.x/ml/3.DecisionTree/DecisionTree.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/3.DecisionTree/DecisionTree.py>
```
收集数据: 可以使用任何方法
准备数据: 树构造算法（这里使用的是ID3算法，因此数值型数据必须离散化。）
分析数据: 可以使用任何方法，构造树完成之后，我们可以将树画出来。
训练算法: 构造树结构
测试算法: 使用习得的决策树执行分类
使用算法: 此步骤可以适用于任何监督学习任务，而使用决策树可以更好地理解数据的内在含义
```
> 收集数据: 可以使用任何方法
![海洋生物数据](http://data.apachecn.org/img/AiLearning/ml/3.DecisionTree/DT_海洋生物数据.png)
我们利用 createDataSet() 函数输入数据
```python
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing', 'flippers']
return dataSet, labels
```
> 准备数据: 树构造算法
此处，由于我们输入的数据本身就是离散化数据，所以这一步就省略了。
> 分析数据: 可以使用任何方法，构造树完成之后，我们可以将树画出来。
![熵的计算公式](http://data.apachecn.org/img/AiLearning/ml/3.DecisionTree/熵的计算公式.jpg)
计算给定数据集的香农熵的函数
```python
def calcShannonEnt(dataSet):
# 求list的长度，表示计算参与训练的数据量
numEntries = len(dataSet)
# 计算分类标签label出现的次数
labelCounts = {}
# the the number of unique elements and their occurrence
for featVec in dataSet:
# 将当前实例的标签存储，即每一行数据的最后一个数据代表的是标签
currentLabel = featVec[-1]
# 为所有可能的分类创建字典，如果当前的键值不存在，则扩展字典并将当前键值加入字典。每个键值都记录了当前类别出现的次数。
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
# 对于 label 标签的占比，求出 label 标签的香农熵
shannonEnt = 0.0
for key in labelCounts:
# 使用所有类标签的发生频率计算类别出现的概率。
prob = float(labelCounts[key])/numEntries
# 计算香农熵，以 2 为底求对数
shannonEnt -= prob * log(prob, 2)
return shannonEnt
```
按照给定特征划分数据集
`将指定特征的特征值等于 value 的行剩下列作为子数据集。`
```python
def splitDataSet(dataSet, index, value):
"""splitDataSet(通过遍历dataSet数据集，求出index对应的colnum列的值为value的行)
就是依据index列进行分类，如果index列的数据等于 value的时候，就要将 index 划分到我们创建的新的数据集中
Args:
dataSet 数据集 待划分的数据集
index 表示每一行的index列 划分数据集的特征
value 表示index列对应的value值 需要返回的特征的值。
Returns:
index列为value的数据集【该数据集需要排除index列】
"""
retDataSet = []
for featVec in dataSet:
# index列为value的数据集【该数据集需要排除index列】
# 判断index列的值是否为value
if featVec[index] == value:
# chop out index used for splitting
# [:index]表示前index行，即若 index 为2，就是取 featVec 的前 index 行
reducedFeatVec = featVec[:index]
'''
请百度查询一下: extend和append的区别
music_media.append(object) 向列表中添加一个对象object
           music_media.extend(sequence) 把一个序列seq的内容添加到列表中 (跟 += 在list运用类似， music_media += sequence)
           1、使用append的时候，是将object看作一个对象，整体打包添加到music_media对象中。
2、使用extend的时候，是将sequence看作一个序列，将这个序列和music_media序列合并，并放在其后面。
music_media = []
music_media.extend([1,2,3])
print music_media
           #结果:
           #[1, 2, 3]
music_media.append([4,5,6])
print music_media
#结果:
           #[1, 2, 3, [4, 5, 6]]
music_media.extend([7,8,9])
print music_media
#结果:
           #[1, 2, 3, [4, 5, 6], 7, 8, 9]
'''
reducedFeatVec.extend(featVec[index+1:])
# [index+1:]表示从跳过 index 的 index+1行，取接下来的数据
# 收集结果值 index列为value的行【该行需要排除index列】
retDataSet.append(reducedFeatVec)
return retDataSet
```
选择最好的数据集划分方式
```python
def chooseBestFeatureToSplit(dataSet):
"""chooseBestFeatureToSplit(选择最好的特征)
Args:
dataSet 数据集
Returns:
bestFeature 最优的特征列
"""
# 求第一行有多少列的 Feature, 最后一列是label列嘛
numFeatures = len(dataSet[0]) - 1
# 数据集的原始信息熵
baseEntropy = calcShannonEnt(dataSet)
# 最优的信息增益值, 和最优的Featurn编号
bestInfoGain, bestFeature = 0.0, -1
# iterate over all the features
for i in range(numFeatures):
# create a list of all the examples of this feature
# 获取对应的feature下的所有数据
featList = [example[i] for example in dataSet]
# get a set of unique values
# 获取剔重后的集合，使用set对list数据进行去重
uniqueVals = set(featList)
# 创建一个临时的信息熵
newEntropy = 0.0
# 遍历某一列的value集合，计算该列的信息熵
# 遍历当前特征中的所有唯一属性值，对每个唯一属性值划分一次数据集，计算数据集的新熵值，并对所有唯一特征值得到的熵求和。
for value in uniqueVals:
subDataSet = splitDataSet(dataSet, i, value)
# 计算概率
prob = len(subDataSet)/float(len(dataSet))
# 计算信息熵
newEntropy += prob * calcShannonEnt(subDataSet)
# gain[信息增益]: 划分数据集前后的信息变化， 获取信息熵最大的值
# 信息增益是熵的减少或者是数据无序度的减少。最后，比较所有特征中的信息增益，返回最好特征划分的索引值。
infoGain = baseEntropy - newEntropy
print 'infoGain=', infoGain, 'bestFeature=', i, baseEntropy, newEntropy
if (infoGain > bestInfoGain):
bestInfoGain = infoGain
bestFeature = i
return bestFeature
```
```
问: 上面的 newEntropy 为什么是根据子集计算的呢？
答: 因为我们在根据一个特征计算香农熵的时候，该特征的分类值是相同，这个特征这个分类的香农熵为 0；
这就是为什么计算新的香农熵的时候使用的是子集。
```
> 训练算法: 构造树的数据结构
创建树的函数代码如下:
```python
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
# 如果数据集的最后一列的第一个值出现的次数=整个集合的数量，也就说只有一个类别，就只直接返回结果就行
# 第一个停止条件: 所有的类标签完全相同，则直接返回该类标签。
# count() 函数是统计括号中的值在list中出现的次数
if classList.count(classList[0]) == len(classList):
return classList[0]
# 如果数据集只有1列，那么最初出现label次数最多的一类，作为结果
# 第二个停止条件: 使用完了所有特征，仍然不能将数据集划分成仅包含唯一类别的分组。
if len(dataSet[0]) == 1:
return majorityCnt(classList)
# 选择最优的列，得到最优列对应的label含义
bestFeat = chooseBestFeatureToSplit(dataSet)
# 获取label的名称
bestFeatLabel = labels[bestFeat]
# 初始化myTree
myTree = {bestFeatLabel: {}}
# 注: labels列表是可变对象，在PYTHON函数中作为参数时传址引用，能够被全局修改
# 所以这行代码导致函数外的同名变量被删除了元素，造成例句无法执行，提示'no surfacing' is not in list
del(labels[bestFeat])
# 取出最优列，然后它的branch做分类
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
# 求出剩余的标签label
subLabels = labels[:]
# 遍历当前选择特征包含的所有属性值，在每个数据集划分上递归调用函数createTree()
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
# print 'myTree', value, myTree
return myTree
```
> 测试算法: 使用决策树执行分类
```python
def classify(inputTree, featLabels, testVec):
"""classify(给输入的节点，进行分类)
Args:
inputTree 决策树模型
featLabels Feature标签对应的名称
testVec 测试输入的数据
Returns:
classLabel 分类的结果值，需要映射label才能知道名称
"""
# 获取tree的根节点对于的key值
firstStr = list(inputTree.keys())[0]
# 通过key得到根节点对应的value
secondDict = inputTree[firstStr]
# 判断根节点名称获取根节点在label中的先后顺序，这样就知道输入的testVec怎么开始对照树来做分类
featIndex = featLabels.index(firstStr)
# 测试数据，找到根节点对应的label位置，也就知道从输入的数据的第几位来开始分类
key = testVec[featIndex]
valueOfFeat = secondDict[key]
print '+++', firstStr, 'xxx', secondDict, '---', key, '>>>', valueOfFeat
# 判断分枝是否结束: 判断valueOfFeat是否是dict类型
if isinstance(valueOfFeat, dict):
classLabel = classify(valueOfFeat, featLabels, testVec)
else:
classLabel = valueOfFeat
return classLabel
```
> 使用算法: 此步骤可以适用于任何监督学习任务，而使用决策树可以更好地理解数据的内在含义。
### 项目案例2: 使用决策树预测隐形眼镜类型
[完整代码地址](/src/py2.x/ml/3.DecisionTree/DecisionTree.py): <https://github.com/apachecn/AiLearning/blob/master/src/py2.x/ml/3.DecisionTree/DecisionTree.py>
#### 项目概述
隐形眼镜类型包括硬材质、软材质以及不适合佩戴隐形眼镜。我们需要使用决策树预测患者需要佩戴的隐形眼镜类型。
#### 开发流程
1. 收集数据: 提供的文本文件。
2. 解析数据: 解析 tab 键分隔的数据行
3. 分析数据: 快速检查数据，确保正确地解析数据内容，使用 createPlot() 函数绘制最终的树形图。
4. 训练算法: 使用 createTree() 函数。
5. 测试算法: 编写测试函数验证决策树可以正确分类给定的数据实例。
6. 使用算法: 存储树的数据结构，以便下次使用时无需重新构造树。
> 收集数据: 提供的文本文件
文本文件数据格式如下:
```
young myope no reduced no lenses
pre myope no reduced no lenses
presbyopic myope no reduced no lenses
```
> 解析数据: 解析 tab 键分隔的数据行
```python
lecses = [inst.strip().split('\t') for inst in fr.readlines()]
lensesLabels = ['age', 'prescript', 'astigmatic', 'tearRate']
```
> 分析数据: 快速检查数据，确保正确地解析数据内容，使用 createPlot() 函数绘制最终的树形图。
```python
>>> treePlotter.createPlot(lensesTree)
```
> 训练算法: 使用 createTree() 函数
```python
>>> lensesTree = trees.createTree(lenses, lensesLabels)
>>> lensesTree
{'tearRate': {'reduced': 'no lenses', 'normal': {'astigmatic':{'yes':
{'prescript':{'hyper':{'age':{'pre':'no lenses', 'presbyopic':
'no lenses', 'young':'hard'}}, 'myope':'hard'}}, 'no':{'age':{'pre':
'soft', 'presbyopic':{'prescript': {'hyper':'soft', 'myope':
'no lenses'}}, 'young':'soft'}}}}}
```
> 测试算法: 编写测试函数验证决策树可以正确分类给定的数据实例。
> 使用算法: 存储树的数据结构，以便下次使用时无需重新构造树。
使用 pickle 模块存储决策树
```python
def storeTree(inputTree, filename):
import pickle
fw = open(filename, 'wb')
pickle.dump(inputTree, fw)
fw.close()
def grabTree(filename):
import pickle
fr = open(filename, 'rb')
return pickle.load(fr)
```
* * *
* **作者: [片刻](https://github.com/jiangzhonglian) [小瑶](http://cwiki.apachecn.org/display/~chenyao)**
* [GitHub地址](https://github.com/apachecn/AiLearning): <https://github.com/apachecn/AiLearning>
* **版权声明: 欢迎转载学习 => 请标注信息来源于 [ApacheCN](http://www.apachecn.org/)**

1588
docs/ml/4.朴素贝叶斯.md → docs/ml/4.md
View File

File diff suppressed because it is too large Load Diff

0
docs/ml/5.Logistic回归.md → docs/ml/5.md
View File

638
docs/ml/6.1.支持向量机的几个通俗理解.md → docs/ml/6.1.md
View File

@@ -1,319 +1,319 @@
# SVM
> 声明
```
阅读本文前，需要您懂一些高等数学、概率论、线性代数的相关知识，以便更好理解。
```
```
下面这些关于 SVM 的理解，是根据知乎和其他博客或者网站中查询到的资料加以整理，
并结合 ApacheCN 这段时间的撸代码和相关研究得到，有理解有误的地方还望大家指出，谢谢。
再次感谢网上的大佬们的无私贡献。
ApacheCN: http://www.apachecn.org/
ApacheCN MachineLearning github: https://github.com/apachecn/AiLearning
网上资料参考链接:https://www.zhihu.com/question/21094489
http://docs.opencv.org/2.4/doc/tutorials/ml/introduction_to_svm/introduction_to_svm.html
https://zhuanlan.zhihu.com/p/26891427?utm_medium=social&utm_source=qq
https://zhuanlan.zhihu.com/p/21308801?utm_medium=social&utm_source=qq
http://blog.csdn.net/v_july_v/article/details/7624837
```
## Overview
### What's the SVM?
^_^ 首先，支持向量机不是一种机器，而是一种机器学习算法。
1、SVM - Support Vector Machine ，俗称支持向量机，是一种 supervised learning （监督学习）算法，属于 classification （分类）的范畴。
2、在数据挖掘的应用中，与 unsupervised learning （无监督学习）的 Clustering（聚类）相对应和区别。
3、广泛应用于 Machine Learning （机器学习），Computer Vision （计算机视觉，装逼一点说，就是 cv）和 Data Mining （数据挖掘）当中。
### “ Machine （机）” 是什么？
Classification Machine，是分类器，这个没什么好说的。也可以理解为算法，机器学习领域里面常常用 “机” 也就是 machine 这个字表示算法。
### “支持向量” 又是什么？
<b>通俗理解</b>:
support vector （支持向量）的意思就是 <b>数据集中的某些点</b>，位置比较特殊。比如 x+y-2=0 这条直线，直线上面区域 x+y-2>0 的全是 A 类，下面的 x+y-2<0 的全是 B 类，我们找这条直线的时候，一般就看聚集在一起的两类数据，他们各自的 <b>最边缘</b> 位置的点，也就是最靠近划分直线的那几个点，而其他点对这条直线的最终位置的确定起不了作用，所以我姑且叫这些点叫 “支持点”（意思就是有用的点），但是在数学上，没这种说法，数学里的点，又可以叫向量，比如 二维点 (x,y) 就是二维向量，三维度的就是三维向量 (x,y,z)。所以 “<b>支持点</b>” 改叫 “<b>支持向量</b>” ，听起来比较专业，而且又装逼，何乐而不为呢？是吧...
<b>不通俗的理解</b>:
在 maximum margin （最大间隔）上的这些点就叫 “支持向量”，我想补充的是为啥这些点就叫 “支持向量” ，因为最后的 classification machine （分类器）的表达式里只含有这些 “支持向量” 的信息，而与其他数据点无关:
![支持向量机公式](http://data.apachecn.org/img/AiLearning/ml/6.SVM/supportVector公式.jpg "supportVector公式")
在这个表达式中，只有支持向量的系数 ![alphai](http://data.apachecn.org/img/AiLearning/ml/6.SVM/alpha.png "alphai") 不等于 0 。
如果还是不怎么理解，不要紧，看下图:
![supportVector](http://data.apachecn.org/img/AiLearning/ml/6.SVM/supportVector.png "supportVector")
“支持向量” 就是图中用紫色框框圈出来的点...
## Concept （相关概念）
我们先看一张图
![supportVectorMachine](http://data.apachecn.org/img/AiLearning/ml/6.SVM/svm_2.png "supportVectorMachine")
`linearly separable （线性可分）`: 如上图中的两组数据，它们之间已经分的足够开了，因此很容易就可以在图中画出一条直线将两组数据点分开。在这种情况下，这组数据就被称为<b>线性可分数据</b>。
`separating hyperplane（分隔超平面）`: 上述将数据集分隔开来的直线称为<b>分隔超平面</b>。
`hyperplane（超平面）`: 在上面给出的例子中，由于数据点都在二维平面上，所以此时分隔超平面就只是一条直线。但是，如果所给的数据集是三维的，那么此时用来分隔数据的就是一个平面。显而易见，更高纬度的情况可以依此类推。如果数据是 1024 维的，那么就需要一个 1023 维的某某对象（不是你们的男（女）票）来对数据进行分隔。这个 1023 维的某某对象到底应该叫什么呢？ N-1 维呢？该对象被称为<b>超平面</b>，也就是分类的决策边界。分布在超平面一侧的所有数据都属于某个类别，而分布在另一侧的所有数据则属于另一个类别。
`margin（间隔）`: 我们希望能通过上述的方式来构建分类器，即如果数据点离决策边界越远，那么其最后的预测结果也就越可信。既然这样，我们希望找到离分隔超平面最近的点，确保它们离分隔面的距离尽可能远。这里所说的点到分隔面的距离就是 <b>间隔</b>。我们希望间隔尽可能地大，这是因为如果我们犯错或者在有限数据上训练分类器的话，我们希望分类器尽可能健壮。
`支持向量（support vector）` : 就是上面所说的离分隔超平面最近的那些点。
`分类器` : 分类器就是给定一个样本的数据，判定这个样本属于哪个类别的算法。例如在股票涨跌预测中，我们认为前一天的交易量和收盘价对于第二天的涨跌是有影响的，那么分类器就是通过样本的交易量和收盘价预测第二天的涨跌情况的算法。
`特征` : 在分类问题中，输入到分类器中的数据叫做特征。以上面的股票涨跌预测问题为例，特征就是前一天的交易量和收盘价。
`线性分类器` : 线性分类器是分类器中的一种，就是判定分类结果的根据是通过特征的线性组合得到的，不能通过特征的非线性运算结果作为判定根据。还以上面的股票涨跌预测问题为例，判断的依据只能是前一天的交易量和收盘价的线性组合，不能将交易量和收盘价进行开方，平方等运算。
## How does it work? （SVM 原理）
### 1、引用知乎上 [@简之](https://www.zhihu.com/people/wangjianzhi/answers) 大佬的回答:
首先我们讲个故事:
在很久以前的情人节，大侠要去救他的爱人，但魔鬼和他玩了一个游戏。
魔鬼在桌子上似乎有规律放了两种颜色的球，说: “你用一根棍分开它们？要求: 尽量在放更多球之后，仍然适用。”
![story_1](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_1.png "story_1")
于是大侠这样放，干的不错？
![story_2](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_2.png "story_2")
然后魔鬼，又在桌上放了更多的球，似乎有一个球站错了阵营。
![story_3](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_3.png "story_3")
SVM 就是试图把棍放在最佳位置，好让在棍的两边有尽可能大的间隙。
![story_4](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_4.png "story_4")
现在即使魔鬼放了更多的球，棍仍然是一个好的分界线。
![story_5](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_5.png "story_5")
然后，在 SVM 工具箱中有另一个更加重要的 trick。 魔鬼看到大侠已经学会了一个 trick ，于是魔鬼给了大侠一个新的挑战。
![story_6](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_6.png "story_6")
现在，大侠没有棍可以很好帮他分开两种球了，现在怎么办呢？当然像所有武侠片中一样大侠桌子一拍，球飞到空中。然后，凭借大侠的轻功，大侠抓起一张纸，插到了两种球的中间。
![story_7](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_7.png "story_7")
现在，从魔鬼的角度看这些球，这些球看起来像是被一条曲线分开了。
![story_8](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_8.png "story_8")
再之后，无聊的大人们，把这些球叫做 <b>「data」</b>，把棍子叫做 <b>「classifier」</b>, 最大间隙 trick 叫做<b>「optimization」</b>， 拍桌子叫做<b>「kernelling」</b>, 那张纸叫做<b>「hyperplane」</b> 。
有梯子的童鞋，可以看一下这个地方，看视频来更直观的感受:
https://www.youtube.com/watch?v=3liCbRZPrZA
### 2、引用知乎 [@开膛手水货](https://www.zhihu.com/people/kai-tang-shou-xin/answers) 大佬的回答，我认为是超级通俗的一个版本:
支持向量机是用来解决分类问题的。
先考虑最简单的情况，豌豆和米粒，用晒子很快可以分开，小颗粒漏下去，大颗粒保留。
用一个函数来表示就是当直径 d 大于某个值 D ，就判定为豌豆，小于某个值就是米粒。
d>D, 豌豆
d<D,米粒
在数轴上就是在d左边就是米粒，右边就是绿豆，这是一维的情况。
但是实际问题没这么简单，考虑的问题不单单是尺寸，一个花的两个品种，怎么分类？
假设决定他们分类的有两个属性，花瓣尺寸和颜色。单独用一个属性来分类，像刚才分米粒那样，就不行了。这个时候我们设置两个值 尺寸 x 和颜色 y.
我们把所有的数据都丢到 x-y 平面上作为点，按道理如果只有这两个属性决定了两个品种，数据肯定会按两类聚集在这个二维平面上。
我们只要找到一条直线，把这两类划分开来，分类就很容易了，以后遇到一个数据，就丢进这个平面，看在直线的哪一边，就是哪一类。
比如 x+y-2=0 这条直线，我们把数据 (x,y) 代入，只要认为 x+y-2>0 的就是 A 类， x+y-2<0 的就是 B 类。
以此类推，还有三维的，四维的，N维的 属性的分类，这样构造的也许就不是直线，而是平面，超平面。
一个三维的函数分类 : x+y+z-2=0，这就是个分类的平面了。
有时候，分类的那条线不一定是直线，还有可能是曲线，我们通过某些函数来转换，就可以转化成刚才的哪种多维的分类问题，这个就是核函数的思想。
例如: 分类的函数是个圆形 x^2+y^2-4=0 。这个时候令 x^2=a ; y^2=b ,还不就变成了a+b-4=0 这种直线问题了。
这就是支持向量机的思想。
### 3、引用 [@胡KF](https://www.zhihu.com/people/hu-kf/answers) 大佬的回答（这个需要一些数学知识）:
如图的例子，（训练集）红色点是我们已知的分类1，（训练集）蓝色点是已知的分类2，我们想寻找一个分隔超平面（图中绿线）（因为示例是二维数据点，所以只是一条线，如果数据是三维的就是平面，如果是三维以上就是超平面）把这两类完全分开，这样的话再来一个样本点需要我们预测的话，我们就可以根据这个分界超平面预测出分类结果。
![hu_1](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_1.jpg "hu_1")
那我们如何选择这个分类超平面呢？从数学上说，超平面的公式是,也就是说如何选取这个 ![w](http://data.apachecn.org/img/AiLearning/ml/6.SVM/w.png "w")（是个向量）。
传统方法是根据最小二乘错误法（least squared error），首先随便定选取一个随机平面，也就是随机选取 ![w](http://data.apachecn.org/img/AiLearning/ml/6.SVM/w.png "w") 和 ![b](http://data.apachecn.org/img/AiLearning/ml/6.SVM/b.png "b")，然后想必会在训练集中产生大量的错误分类，也就是说，![wtx+b](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_5.png "wtx+b") 结果应该大于 0 的时候小于 0 ，应该小于 0 的时候大于 0 。这时候有一个错误损失，也就是说对于所有错误的分类，他们的平方和（least squared error） 为: ![平方和](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_8.png "平方和") , 最小二乘法的目标就是让这个值趋于最小，对 ![w](http://data.apachecn.org/img/AiLearning/ml/6.SVM/w.png "w") 求导取 0 ，采用梯度下降算法，可以求出错误平方和的极值，求出最优的 ![w](http://data.apachecn.org/img/AiLearning/ml/6.SVM/w.png "w") ，也就是求出最优的超平面。（可以证明，如果基函数是指数族函数，求出的超平面是全局最优的）。
那我们 SVM 算法的思路是怎样的呢？
不同于传统的最小二乘策略的思想，我们采用一种新的思路，这个分界面有什么样的特征呢？
第一，它 “夹” 在两类样本点之间；第二，它离两类样本点中所有 “离它最近的点” ，都离它尽可能的远。如图所示:
![hu_2](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_2.jpg "hu_2")
在虚线上的点，就是我们所找到的离分解超平面最近的样本点，X 类中找到了一个，O 类找到了两个。我们需要分类超平面离这三个样本点都尽可能的远，也就是说，它处在两条虚线的中间。这就是我们找到的分界超平面。
另外，这里我们就可以解释什么是 “支持向量” 了，支持向量就是虚线上的离分类超平面最近的样本点，因为每一个样本点都是一个多维的向量，向量的每一个维度都是这个样本点的一个特征。比如在根据身高，体重，特征进行男女分类的时候，每一个人是一个向量，向量有两个维度，第一维是身高，第二维是体重。
介绍完 SVM 的基本思想，我们来探讨一下如何用数学的方法进行 SVM 分类。
首先我们需要把刚刚说的最大间隔分类器的思想用数学公式表达出来。先定义几何间隔的概念，几何间隔就是在多维空间中一个多维点到一个超平面的距离，根据向量的知识可以算出来:
![hu_3](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_3.png "hu_3")
然后对于所有的支持向量，使他们到超平面 ![hu_5](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_5.png "hu_5") 的距离最大，也就是
![hu_4](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_4.png "hu_4")
因为对于所有支持向量，他们 ![hu_5](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_5.png "hu_5") 的值都是一定的，我们假设恒等于 1 ，那么上式变成了 ![hu_6](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_6.png "hu_6") ,并且对于所有的样本点，满足 ![hu_10](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_10.png "hu_10") 的约束，因此，可以利用拉格朗日乘数法计算出它的极值。也就是求出这个超平面。
推导过程略为复杂，详细了解可以参考凸二次规划知识，结合 SMO 算法理解 SVM 计算超平面的详细过程。
总之，在计算的过程中，我们不需要了解支持向量以外的其他样本点，只需要利用相对于所有样本点来说为数不多的支持向量，就可以求出分类超平面，计算复杂度大为降低。
### 4、引用知乎 [@靠靠靠谱](https://www.zhihu.com/people/kao-kao-kao-pu/answers) 大佬的理解（这个需要的数学知识更加厉害一点）:
先看思维导图:
* 左边是求解基本的SVM问题
* 右边是相关扩展
![k_1](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_1.jpg "k_1")
<b>什么是 SVM ？</b>
Support Vector Machine, 一个普通的 SVM 就是一条直线罢了，用来完美划分 linearly separable 的两类。但这又不是一条普通的直线，这是无数条可以分类的直线当中最完美的，因为它恰好在两个类的中间，距离两个类的点都一样远。而所谓的 Support vector 就是这些离分界线最近的『点』。如果去掉这些点，直线多半是要改变位置的。可以说是这些 vectors （主，点点） support （谓，定义）了 machine （宾，分类器）...
![k_2](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_2.jpg "k_2")
所以谜底就在谜面上啊朋友们，只要找到了这些最靠近的点不就找到了 SVM 了嘛。
如果是高维的点，SVM 的分界线就是平面或者超平面。其实没有差，都是一刀切两块，我就统统叫直线了。
<b>怎么求解 SVM ？</b>
关于这条直线，我们知道
(1)它离两边一样远，(2)最近距离就是到support vector的距离，其他距离只能更远。
于是自然而然可以得到重要表达 <b>I. direct representation</b>
![k_7](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_7.png "k_7")
（可以把 margin 看作是 boundary 的函数，并且想要找到使得是使得 margin 最大化的boundary，而 margin(*) 这个函数是: 输入一个 boundary ，计算（正确分类的）所有苹果和香蕉中，到 boundary 的最小距离。）
又有最大又有最小看起来好矛盾。实际上『最大』是对这个整体使用不同 boundary 层面的最大，『最小』是在比较『点』的层面上的最小。外层在比较 boundary 找最大的 margin ，内层在比较点点找最小的距离。
其中距离，说白了就是点到直线的距离；只要定义带正负号的距离，是 {苹果+1} 面为正 {香蕉-1} 面为负的距离，互相乘上各自的 label ![k_8](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_8.png "k_8") ，就和谐统一民主富强了。
![k_9](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_9.png "k_9")
到这里为止已经说完了所有关于SVM的直观了解，如果不想看求解，可以跳过下面一大段直接到 objective function 。
直接表达虽然清楚但是求解无从下手。做一些简单地等价变换（分母倒上来）可以得到 <b>II. canonical representation </b> （敲黑板）
![k_10](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_10.png "k_10")
要得到 <b>III. dual representation</b> 之前需要大概知道一下拉格朗日乘子法 (method of lagrange multiplier)，它是用在有各种约束条件(各种 "subject to" )下的目标函数，也就是直接可以求导可以引出 dual representation（怎么还没完摔）
![k_11](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_11.png "k_11")
稍微借用刚刚数学表达里面的内容看个有趣的东西:
还记得我们怎么预测一个新的水果是苹果还是香蕉吗？我们代入到分界的直线里，然后通过符号来判断。
刚刚w已经被表达出来了也就是说这个直线现在变成了: ![k_12](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_12.png "k_12")
看似仿佛用到了所有的训练水果，但是其中 ![k_13](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_13.png "k_13") 的水果都没有起到作用，剩下的就是小部分靠边边的 Support vectors 呀。
<b>III. dual representation</b>
![k_14](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_14.png "k_14")
<b>如果香蕉和苹果不能用直线分割呢？</b>
![k_3](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_3.jpg "k_3")
Kernel trick.
其实用直线分割的时候我们已经使用了 kernel ，那就是线性 kernel , ![k_15](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_15.png "k_15")
如果要替换 kernel 那么把目标函数里面的内积全部替换成新的 kernel function 就好了，就是这么简单。
第一个武侠大师的比喻已经说得很直观了，低维非线性的分界线其实在高维是可以线性分割的，可以理解为——『你们是虫子！』分得开个p...（大雾）
<b>如果香蕉和苹果有交集呢？</b>
![k_4](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_4.jpg "k_4")
![k_16](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_16.png "k_16")
<b>如果还有梨呢？</b>
![k_5](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_5.jpg "k_5")
可以每个类别做一次 SVM: 是苹果还是不是苹果？是香蕉还是不是香蕉？是梨子还是不是梨子？从中选出可能性最大的。这是 one-versus-the-rest approach。
也可以两两做一次 SVM: 是苹果还是香蕉？是香蕉还是梨子？是梨子还是苹果？最后三个分类器投票决定。这是 one-versus-one approace。
但这其实都多多少少有问题，比如苹果特别多，香蕉特别少，我就无脑判断为苹果也不会错太多；多个分类器要放到一个台面上，万一他们的 scale 没有在一个台面上也未可知。
课后题:
1、vector 不愿意 support 怎么办？
2、苹果好吃还是香蕉好吃？
<p>最后送一张图我好爱哈哈哈 (Credit: Burr Settles)</p>
![k_6](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_6.png "k_6")
<p>[1] Bishop C M. Pattern recognition[J]. Machine Learning, 2006, 128.</p>
<p>[2] Friedman J, Hastie T, Tibshirani R. The elements of statistical learning[M]. Springer, Berlin: Springer series in statistics, 2001.</p>
<p>[3] James G, Witten D, Hastie T, et al. An introduction to statistical learning[M]. New York: springer, 2013.</p>
## 理解和应用
### 1、DataMining （数据挖掘）
做数据挖掘应用的一种重要算法，也是效果最好的分类算法之一。
举个例子，就是尽量把样本中的从更高纬度看起来在一起的样本合在一起，比如在一维（直线）空间里的样本从二维平面上可以分成不同类别，而在二维平面上分散的样本如果从第三维空间上来看就可以对他们做分类。
支持向量机算法目的是找出最优超平面，使分类间隔最大，要求不但正确分开，而且使分类间隔最大，在两类样本中离分类平面最近且位于平行于最优超平面的超平面上的点就是支持向量，为找到最优超平面只要找到所有支持向量即可。
对于非线性支持向量机，通常做法是把线性不可分转化成线性可分，通过一个非线性映射将输入到低维空间中的数据特性映射到高维线性特征空间中，在高维空间中求线性最优分类超平面。
### 2、scikit-learn (sklearn)
SVM 的基本原理基本上已经说的差不多了，下面咱们就来看看 SVM 在实际应用该如何使用了。幸运的是，在 python 下面，sklearn 提供了一个非常好用的机器学习算法，我们调用相关的包就好啦。
![sklearn_map](http://data.apachecn.org/img/AiLearning/ml/6.SVM/ml_map.png "sklearn")
## 小结
学习 SVM 需要有耐心，当初研究这个部分的时候，炼哥（github [jiangzhonglian](https://github.com/jiangzhonglian)），法超大佬（github [geekidentity](https://github.com/geekidentity)），羊三大佬（github [sheepmen](https://github.com/sheepmen)），庭哥（github [wangyangting](https://github.com/wangyangting)）都花费了好长时间，我只能躲在角落发抖....
# SVM
> 声明
```
阅读本文前，需要您懂一些高等数学、概率论、线性代数的相关知识，以便更好理解。
```
```
下面这些关于 SVM 的理解，是根据知乎和其他博客或者网站中查询到的资料加以整理，
并结合 ApacheCN 这段时间的撸代码和相关研究得到，有理解有误的地方还望大家指出，谢谢。
再次感谢网上的大佬们的无私贡献。
ApacheCN: http://www.apachecn.org/
ApacheCN MachineLearning github: https://github.com/apachecn/AiLearning
网上资料参考链接:https://www.zhihu.com/question/21094489
http://docs.opencv.org/2.4/doc/tutorials/ml/introduction_to_svm/introduction_to_svm.html
https://zhuanlan.zhihu.com/p/26891427?utm_medium=social&utm_source=qq
https://zhuanlan.zhihu.com/p/21308801?utm_medium=social&utm_source=qq
http://blog.csdn.net/v_july_v/article/details/7624837
```
## Overview
### What's the SVM?
^_^ 首先，支持向量机不是一种机器，而是一种机器学习算法。
1、SVM - Support Vector Machine ，俗称支持向量机，是一种 supervised learning （监督学习）算法，属于 classification （分类）的范畴。
2、在数据挖掘的应用中，与 unsupervised learning （无监督学习）的 Clustering（聚类）相对应和区别。
3、广泛应用于 Machine Learning （机器学习），Computer Vision （计算机视觉，装逼一点说，就是 cv）和 Data Mining （数据挖掘）当中。
### “ Machine （机）” 是什么？
Classification Machine，是分类器，这个没什么好说的。也可以理解为算法，机器学习领域里面常常用 “机” 也就是 machine 这个字表示算法。
### “支持向量” 又是什么？
<b>通俗理解</b>:
support vector （支持向量）的意思就是 <b>数据集中的某些点</b>，位置比较特殊。比如 x+y-2=0 这条直线，直线上面区域 x+y-2>0 的全是 A 类，下面的 x+y-2<0 的全是 B 类，我们找这条直线的时候，一般就看聚集在一起的两类数据，他们各自的 <b>最边缘</b> 位置的点，也就是最靠近划分直线的那几个点，而其他点对这条直线的最终位置的确定起不了作用，所以我姑且叫这些点叫 “支持点”（意思就是有用的点），但是在数学上，没这种说法，数学里的点，又可以叫向量，比如 二维点 (x,y) 就是二维向量，三维度的就是三维向量 (x,y,z)。所以 “<b>支持点</b>” 改叫 “<b>支持向量</b>” ，听起来比较专业，而且又装逼，何乐而不为呢？是吧...
<b>不通俗的理解</b>:
在 maximum margin （最大间隔）上的这些点就叫 “支持向量”，我想补充的是为啥这些点就叫 “支持向量” ，因为最后的 classification machine （分类器）的表达式里只含有这些 “支持向量” 的信息，而与其他数据点无关:
![支持向量机公式](http://data.apachecn.org/img/AiLearning/ml/6.SVM/supportVector公式.jpg "supportVector公式")
在这个表达式中，只有支持向量的系数 ![alphai](http://data.apachecn.org/img/AiLearning/ml/6.SVM/alpha.png "alphai") 不等于 0 。
如果还是不怎么理解，不要紧，看下图:
![supportVector](http://data.apachecn.org/img/AiLearning/ml/6.SVM/supportVector.png "supportVector")
“支持向量” 就是图中用紫色框框圈出来的点...
## Concept （相关概念）
我们先看一张图
![supportVectorMachine](http://data.apachecn.org/img/AiLearning/ml/6.SVM/svm_2.png "supportVectorMachine")
`linearly separable （线性可分）`: 如上图中的两组数据，它们之间已经分的足够开了，因此很容易就可以在图中画出一条直线将两组数据点分开。在这种情况下，这组数据就被称为<b>线性可分数据</b>。
`separating hyperplane（分隔超平面）`: 上述将数据集分隔开来的直线称为<b>分隔超平面</b>。
`hyperplane（超平面）`: 在上面给出的例子中，由于数据点都在二维平面上，所以此时分隔超平面就只是一条直线。但是，如果所给的数据集是三维的，那么此时用来分隔数据的就是一个平面。显而易见，更高纬度的情况可以依此类推。如果数据是 1024 维的，那么就需要一个 1023 维的某某对象（不是你们的男（女）票）来对数据进行分隔。这个 1023 维的某某对象到底应该叫什么呢？ N-1 维呢？该对象被称为<b>超平面</b>，也就是分类的决策边界。分布在超平面一侧的所有数据都属于某个类别，而分布在另一侧的所有数据则属于另一个类别。
`margin（间隔）`: 我们希望能通过上述的方式来构建分类器，即如果数据点离决策边界越远，那么其最后的预测结果也就越可信。既然这样，我们希望找到离分隔超平面最近的点，确保它们离分隔面的距离尽可能远。这里所说的点到分隔面的距离就是 <b>间隔</b>。我们希望间隔尽可能地大，这是因为如果我们犯错或者在有限数据上训练分类器的话，我们希望分类器尽可能健壮。
`支持向量（support vector）` : 就是上面所说的离分隔超平面最近的那些点。
`分类器` : 分类器就是给定一个样本的数据，判定这个样本属于哪个类别的算法。例如在股票涨跌预测中，我们认为前一天的交易量和收盘价对于第二天的涨跌是有影响的，那么分类器就是通过样本的交易量和收盘价预测第二天的涨跌情况的算法。
`特征` : 在分类问题中，输入到分类器中的数据叫做特征。以上面的股票涨跌预测问题为例，特征就是前一天的交易量和收盘价。
`线性分类器` : 线性分类器是分类器中的一种，就是判定分类结果的根据是通过特征的线性组合得到的，不能通过特征的非线性运算结果作为判定根据。还以上面的股票涨跌预测问题为例，判断的依据只能是前一天的交易量和收盘价的线性组合，不能将交易量和收盘价进行开方，平方等运算。
## How does it work? （SVM 原理）
### 1、引用知乎上 [@简之](https://www.zhihu.com/people/wangjianzhi/answers) 大佬的回答:
首先我们讲个故事:
在很久以前的情人节，大侠要去救他的爱人，但魔鬼和他玩了一个游戏。
魔鬼在桌子上似乎有规律放了两种颜色的球，说: “你用一根棍分开它们？要求: 尽量在放更多球之后，仍然适用。”
![story_1](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_1.png "story_1")
于是大侠这样放，干的不错？
![story_2](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_2.png "story_2")
然后魔鬼，又在桌上放了更多的球，似乎有一个球站错了阵营。
![story_3](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_3.png "story_3")
SVM 就是试图把棍放在最佳位置，好让在棍的两边有尽可能大的间隙。
![story_4](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_4.png "story_4")
现在即使魔鬼放了更多的球，棍仍然是一个好的分界线。
![story_5](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_5.png "story_5")
然后，在 SVM 工具箱中有另一个更加重要的 trick。 魔鬼看到大侠已经学会了一个 trick ，于是魔鬼给了大侠一个新的挑战。
![story_6](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_6.png "story_6")
现在，大侠没有棍可以很好帮他分开两种球了，现在怎么办呢？当然像所有武侠片中一样大侠桌子一拍，球飞到空中。然后，凭借大侠的轻功，大侠抓起一张纸，插到了两种球的中间。
![story_7](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_7.png "story_7")
现在，从魔鬼的角度看这些球，这些球看起来像是被一条曲线分开了。
![story_8](http://data.apachecn.org/img/AiLearning/ml/6.SVM/story_8.png "story_8")
再之后，无聊的大人们，把这些球叫做 <b>「data」</b>，把棍子叫做 <b>「classifier」</b>, 最大间隙 trick 叫做<b>「optimization」</b>， 拍桌子叫做<b>「kernelling」</b>, 那张纸叫做<b>「hyperplane」</b> 。
有梯子的童鞋，可以看一下这个地方，看视频来更直观的感受:
https://www.youtube.com/watch?v=3liCbRZPrZA
### 2、引用知乎 [@开膛手水货](https://www.zhihu.com/people/kai-tang-shou-xin/answers) 大佬的回答，我认为是超级通俗的一个版本:
支持向量机是用来解决分类问题的。
先考虑最简单的情况，豌豆和米粒，用晒子很快可以分开，小颗粒漏下去，大颗粒保留。
用一个函数来表示就是当直径 d 大于某个值 D ，就判定为豌豆，小于某个值就是米粒。
d>D, 豌豆
d<D,米粒
在数轴上就是在d左边就是米粒，右边就是绿豆，这是一维的情况。
但是实际问题没这么简单，考虑的问题不单单是尺寸，一个花的两个品种，怎么分类？
假设决定他们分类的有两个属性，花瓣尺寸和颜色。单独用一个属性来分类，像刚才分米粒那样，就不行了。这个时候我们设置两个值 尺寸 x 和颜色 y.
我们把所有的数据都丢到 x-y 平面上作为点，按道理如果只有这两个属性决定了两个品种，数据肯定会按两类聚集在这个二维平面上。
我们只要找到一条直线，把这两类划分开来，分类就很容易了，以后遇到一个数据，就丢进这个平面，看在直线的哪一边，就是哪一类。
比如 x+y-2=0 这条直线，我们把数据 (x,y) 代入，只要认为 x+y-2>0 的就是 A 类， x+y-2<0 的就是 B 类。
以此类推，还有三维的，四维的，N维的 属性的分类，这样构造的也许就不是直线，而是平面，超平面。
一个三维的函数分类 : x+y+z-2=0，这就是个分类的平面了。
有时候，分类的那条线不一定是直线，还有可能是曲线，我们通过某些函数来转换，就可以转化成刚才的哪种多维的分类问题，这个就是核函数的思想。
例如: 分类的函数是个圆形 x^2+y^2-4=0 。这个时候令 x^2=a ; y^2=b ,还不就变成了a+b-4=0 这种直线问题了。
这就是支持向量机的思想。
### 3、引用 [@胡KF](https://www.zhihu.com/people/hu-kf/answers) 大佬的回答（这个需要一些数学知识）:
如图的例子，（训练集）红色点是我们已知的分类1，（训练集）蓝色点是已知的分类2，我们想寻找一个分隔超平面（图中绿线）（因为示例是二维数据点，所以只是一条线，如果数据是三维的就是平面，如果是三维以上就是超平面）把这两类完全分开，这样的话再来一个样本点需要我们预测的话，我们就可以根据这个分界超平面预测出分类结果。
![hu_1](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_1.jpg "hu_1")
那我们如何选择这个分类超平面呢？从数学上说，超平面的公式是,也就是说如何选取这个 ![w](http://data.apachecn.org/img/AiLearning/ml/6.SVM/w.png "w")（是个向量）。
传统方法是根据最小二乘错误法（least squared error），首先随便定选取一个随机平面，也就是随机选取 ![w](http://data.apachecn.org/img/AiLearning/ml/6.SVM/w.png "w") 和 ![b](http://data.apachecn.org/img/AiLearning/ml/6.SVM/b.png "b")，然后想必会在训练集中产生大量的错误分类，也就是说，![wtx+b](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_5.png "wtx+b") 结果应该大于 0 的时候小于 0 ，应该小于 0 的时候大于 0 。这时候有一个错误损失，也就是说对于所有错误的分类，他们的平方和（least squared error） 为: ![平方和](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_8.png "平方和") , 最小二乘法的目标就是让这个值趋于最小，对 ![w](http://data.apachecn.org/img/AiLearning/ml/6.SVM/w.png "w") 求导取 0 ，采用梯度下降算法，可以求出错误平方和的极值，求出最优的 ![w](http://data.apachecn.org/img/AiLearning/ml/6.SVM/w.png "w") ，也就是求出最优的超平面。（可以证明，如果基函数是指数族函数，求出的超平面是全局最优的）。
那我们 SVM 算法的思路是怎样的呢？
不同于传统的最小二乘策略的思想，我们采用一种新的思路，这个分界面有什么样的特征呢？
第一，它 “夹” 在两类样本点之间；第二，它离两类样本点中所有 “离它最近的点” ，都离它尽可能的远。如图所示:
![hu_2](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_2.jpg "hu_2")
在虚线上的点，就是我们所找到的离分解超平面最近的样本点，X 类中找到了一个，O 类找到了两个。我们需要分类超平面离这三个样本点都尽可能的远，也就是说，它处在两条虚线的中间。这就是我们找到的分界超平面。
另外，这里我们就可以解释什么是 “支持向量” 了，支持向量就是虚线上的离分类超平面最近的样本点，因为每一个样本点都是一个多维的向量，向量的每一个维度都是这个样本点的一个特征。比如在根据身高，体重，特征进行男女分类的时候，每一个人是一个向量，向量有两个维度，第一维是身高，第二维是体重。
介绍完 SVM 的基本思想，我们来探讨一下如何用数学的方法进行 SVM 分类。
首先我们需要把刚刚说的最大间隔分类器的思想用数学公式表达出来。先定义几何间隔的概念，几何间隔就是在多维空间中一个多维点到一个超平面的距离，根据向量的知识可以算出来:
![hu_3](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_3.png "hu_3")
然后对于所有的支持向量，使他们到超平面 ![hu_5](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_5.png "hu_5") 的距离最大，也就是
![hu_4](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_4.png "hu_4")
因为对于所有支持向量，他们 ![hu_5](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_5.png "hu_5") 的值都是一定的，我们假设恒等于 1 ，那么上式变成了 ![hu_6](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_6.png "hu_6") ,并且对于所有的样本点，满足 ![hu_10](http://data.apachecn.org/img/AiLearning/ml/6.SVM/hu_10.png "hu_10") 的约束，因此，可以利用拉格朗日乘数法计算出它的极值。也就是求出这个超平面。
推导过程略为复杂，详细了解可以参考凸二次规划知识，结合 SMO 算法理解 SVM 计算超平面的详细过程。
总之，在计算的过程中，我们不需要了解支持向量以外的其他样本点，只需要利用相对于所有样本点来说为数不多的支持向量，就可以求出分类超平面，计算复杂度大为降低。
### 4、引用知乎 [@靠靠靠谱](https://www.zhihu.com/people/kao-kao-kao-pu/answers) 大佬的理解（这个需要的数学知识更加厉害一点）:
先看思维导图:
* 左边是求解基本的SVM问题
* 右边是相关扩展
![k_1](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_1.jpg "k_1")
<b>什么是 SVM ？</b>
Support Vector Machine, 一个普通的 SVM 就是一条直线罢了，用来完美划分 linearly separable 的两类。但这又不是一条普通的直线，这是无数条可以分类的直线当中最完美的，因为它恰好在两个类的中间，距离两个类的点都一样远。而所谓的 Support vector 就是这些离分界线最近的『点』。如果去掉这些点，直线多半是要改变位置的。可以说是这些 vectors （主，点点） support （谓，定义）了 machine （宾，分类器）...
![k_2](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_2.jpg "k_2")
所以谜底就在谜面上啊朋友们，只要找到了这些最靠近的点不就找到了 SVM 了嘛。
如果是高维的点，SVM 的分界线就是平面或者超平面。其实没有差，都是一刀切两块，我就统统叫直线了。
<b>怎么求解 SVM ？</b>
关于这条直线，我们知道
(1)它离两边一样远，(2)最近距离就是到support vector的距离，其他距离只能更远。
于是自然而然可以得到重要表达 <b>I. direct representation</b>
![k_7](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_7.png "k_7")
（可以把 margin 看作是 boundary 的函数，并且想要找到使得是使得 margin 最大化的boundary，而 margin(*) 这个函数是: 输入一个 boundary ，计算（正确分类的）所有苹果和香蕉中，到 boundary 的最小距离。）
又有最大又有最小看起来好矛盾。实际上『最大』是对这个整体使用不同 boundary 层面的最大，『最小』是在比较『点』的层面上的最小。外层在比较 boundary 找最大的 margin ，内层在比较点点找最小的距离。
其中距离，说白了就是点到直线的距离；只要定义带正负号的距离，是 {苹果+1} 面为正 {香蕉-1} 面为负的距离，互相乘上各自的 label ![k_8](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_8.png "k_8") ，就和谐统一民主富强了。
![k_9](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_9.png "k_9")
到这里为止已经说完了所有关于SVM的直观了解，如果不想看求解，可以跳过下面一大段直接到 objective function 。
直接表达虽然清楚但是求解无从下手。做一些简单地等价变换（分母倒上来）可以得到 <b>II. canonical representation </b> （敲黑板）
![k_10](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_10.png "k_10")
要得到 <b>III. dual representation</b> 之前需要大概知道一下拉格朗日乘子法 (method of lagrange multiplier)，它是用在有各种约束条件(各种 "subject to" )下的目标函数，也就是直接可以求导可以引出 dual representation（怎么还没完摔）
![k_11](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_11.png "k_11")
稍微借用刚刚数学表达里面的内容看个有趣的东西:
还记得我们怎么预测一个新的水果是苹果还是香蕉吗？我们代入到分界的直线里，然后通过符号来判断。
刚刚w已经被表达出来了也就是说这个直线现在变成了: ![k_12](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_12.png "k_12")
看似仿佛用到了所有的训练水果，但是其中 ![k_13](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_13.png "k_13") 的水果都没有起到作用，剩下的就是小部分靠边边的 Support vectors 呀。
<b>III. dual representation</b>
![k_14](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_14.png "k_14")
<b>如果香蕉和苹果不能用直线分割呢？</b>
![k_3](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_3.jpg "k_3")
Kernel trick.
其实用直线分割的时候我们已经使用了 kernel ，那就是线性 kernel , ![k_15](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_15.png "k_15")
如果要替换 kernel 那么把目标函数里面的内积全部替换成新的 kernel function 就好了，就是这么简单。
第一个武侠大师的比喻已经说得很直观了，低维非线性的分界线其实在高维是可以线性分割的，可以理解为——『你们是虫子！』分得开个p...（大雾）
<b>如果香蕉和苹果有交集呢？</b>
![k_4](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_4.jpg "k_4")
![k_16](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_16.png "k_16")
<b>如果还有梨呢？</b>
![k_5](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_5.jpg "k_5")
可以每个类别做一次 SVM: 是苹果还是不是苹果？是香蕉还是不是香蕉？是梨子还是不是梨子？从中选出可能性最大的。这是 one-versus-the-rest approach。
也可以两两做一次 SVM: 是苹果还是香蕉？是香蕉还是梨子？是梨子还是苹果？最后三个分类器投票决定。这是 one-versus-one approace。
但这其实都多多少少有问题，比如苹果特别多，香蕉特别少，我就无脑判断为苹果也不会错太多；多个分类器要放到一个台面上，万一他们的 scale 没有在一个台面上也未可知。
课后题:
1、vector 不愿意 support 怎么办？
2、苹果好吃还是香蕉好吃？
<p>最后送一张图我好爱哈哈哈 (Credit: Burr Settles)</p>
![k_6](http://data.apachecn.org/img/AiLearning/ml/6.SVM/k_6.png "k_6")
<p>[1] Bishop C M. Pattern recognition[J]. Machine Learning, 2006, 128.</p>
<p>[2] Friedman J, Hastie T, Tibshirani R. The elements of statistical learning[M]. Springer, Berlin: Springer series in statistics, 2001.</p>
<p>[3] James G, Witten D, Hastie T, et al. An introduction to statistical learning[M]. New York: springer, 2013.</p>
## 理解和应用
### 1、DataMining （数据挖掘）
做数据挖掘应用的一种重要算法，也是效果最好的分类算法之一。
举个例子，就是尽量把样本中的从更高纬度看起来在一起的样本合在一起，比如在一维（直线）空间里的样本从二维平面上可以分成不同类别，而在二维平面上分散的样本如果从第三维空间上来看就可以对他们做分类。
支持向量机算法目的是找出最优超平面，使分类间隔最大，要求不但正确分开，而且使分类间隔最大，在两类样本中离分类平面最近且位于平行于最优超平面的超平面上的点就是支持向量，为找到最优超平面只要找到所有支持向量即可。
对于非线性支持向量机，通常做法是把线性不可分转化成线性可分，通过一个非线性映射将输入到低维空间中的数据特性映射到高维线性特征空间中，在高维空间中求线性最优分类超平面。
### 2、scikit-learn (sklearn)
SVM 的基本原理基本上已经说的差不多了，下面咱们就来看看 SVM 在实际应用该如何使用了。幸运的是，在 python 下面，sklearn 提供了一个非常好用的机器学习算法，我们调用相关的包就好啦。
![sklearn_map](http://data.apachecn.org/img/AiLearning/ml/6.SVM/ml_map.png "sklearn")
## 小结
学习 SVM 需要有耐心，当初研究这个部分的时候，炼哥（github [jiangzhonglian](https://github.com/jiangzhonglian)），法超大佬（github [geekidentity](https://github.com/geekidentity)），羊三大佬（github [sheepmen](https://github.com/sheepmen)），庭哥（github [wangyangting](https://github.com/wangyangting)）都花费了好长时间，我只能躲在角落发抖....

1136
docs/ml/6.支持向量机.md → docs/ml/6.md
View File

File diff suppressed because it is too large Load Diff

1320
docs/ml/7.集成方法-随机森林和AdaBoost.md → docs/ml/7.md
View File

File diff suppressed because it is too large Load Diff

1696
docs/ml/8.回归.md → docs/ml/8.md
View File

File diff suppressed because it is too large Load Diff

1266
docs/ml/9.树回归.md → docs/ml/9.md
View File

File diff suppressed because it is too large Load Diff

0
report/2017-04-08_第一期的总结.md → docs/report/2017-04-08.md
View File