2020-10-19 21:22:54
@@ -50,7 +50,7 @@
|
||||
|
||||
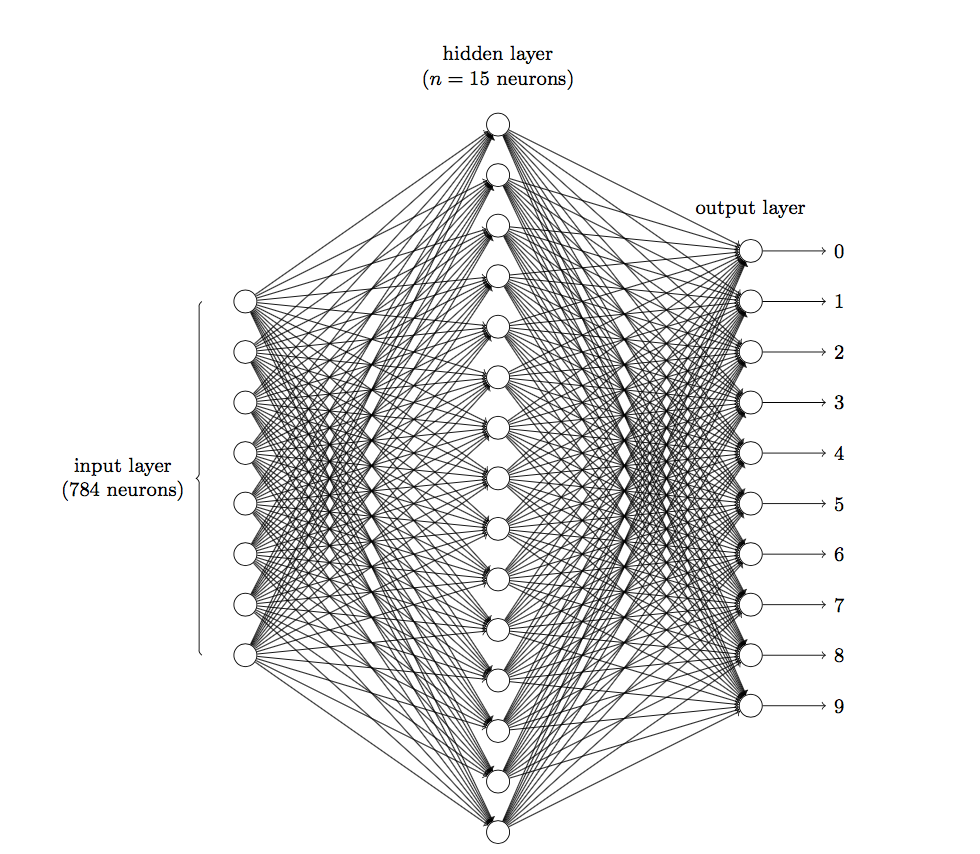
前面说到在图像领域,用传统的神经网络并不合适。我们知道,图像是由一个个像素点构成,每个像素点有三个通道,分别代表RGB颜色,那么,如果一个图像的尺寸是(28,28,1),即代表这个图像的是一个长宽均为28,channel为1的图像(channel也叫depth,此处1代表灰色图像)。如果使用全连接的网络结构,即,网络中的神经与与相邻层上的每个神经元均连接,那就意味着我们的网络有 `28 * 28 =784` 个神经元,hidden层采用了15个神经元,那么简单计算一下,我们需要的参数个数(w和b)就有: `784*15*10+15+10=117625` 个,这个参数太多了,随便进行一次反向传播计算量都是巨大的,从计算资源和调参的角度都不建议用传统的神经网络。(评论中有同学对这个参数计算不太理解,我简单说一下: 图片是由像素点组成的,用矩阵表示的, `28*28` 的矩阵,肯定是没法直接放到神经元里的,我们得把它“拍平”,变成一个`28*28=784` 的一列向量,这一列向量和隐含层的15个神经元连接,就有 `784*15=11760` 个权重w,隐含层和最后的输出层的10个神经元连接,就有 `11760*10=117600` 个权重w,再加上隐含层的偏置项15个和输出层的偏置项10个,就是: 117625个参数了)
|
||||
|
||||
|
||||

|
||||
|
||||
图1 三层神经网络识别手写数字
|
||||
|
||||
@@ -62,7 +62,7 @@
|
||||
|
||||
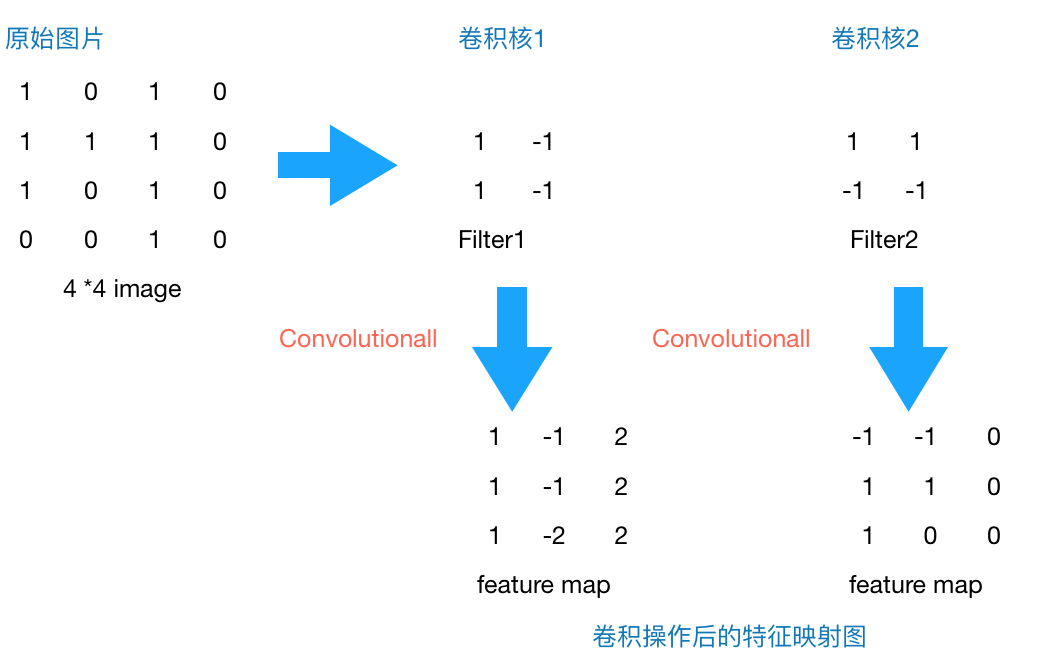
上文提到我们用传统的三层神经网络需要大量的参数,原因在于每个神经元都和相邻层的神经元相连接,但是思考一下,这种连接方式是必须的吗?全连接层的方式对于图像数据来说似乎显得不这么友好,因为图像本身具有“二维空间特征”,通俗点说就是局部特性。譬如我们看一张猫的图片,可能看到猫的眼镜或者嘴巴就知道这是张猫片,而不需要说每个部分都看完了才知道,啊,原来这个是猫啊。所以如果我们可以用某种方式对一张图片的某个典型特征识别,那么这张图片的类别也就知道了。这个时候就产生了卷积的概念。举个例子,现在有一个4*4的图像,我们设计两个卷积核,看看运用卷积核后图片会变成什么样。
|
||||
|
||||
|
||||

|
||||
|
||||
图2 4*4 image与两个2*2的卷积核操作结果
|
||||
|
||||
@@ -532,7 +532,7 @@ class LayerHelper(object):
|
||||
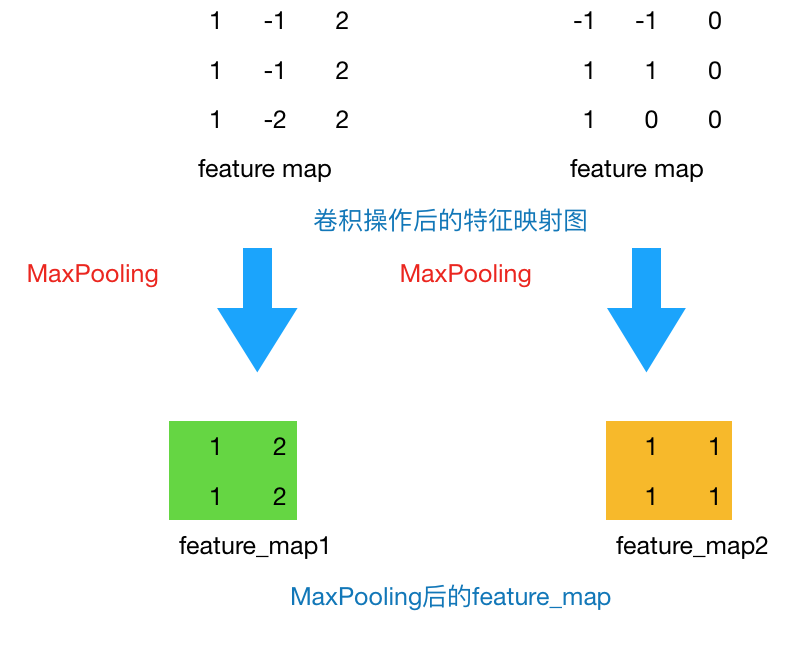
通过上一层2*2的卷积核操作后,我们将原始图像由4*4的尺寸变为了3*3的一个新的图片。池化层的主要目的是通过降采样的方式,在不影响图像质量的情况下,压缩图片,减少参数。简单来说,假设现在设定池化层采用MaxPooling,大小为2*2,步长为1,取每个窗口最大的数值重新,那么图片的尺寸就会由3*3变为2*2: (3-2)+1=2。从上例来看,会有如下变换:
|
||||
|
||||
|
||||
|
||||

|
||||
|
||||
图3 Max Pooling结果
|
||||
|
||||
@@ -553,7 +553,7 @@ class LayerHelper(object):
|
||||
|
||||
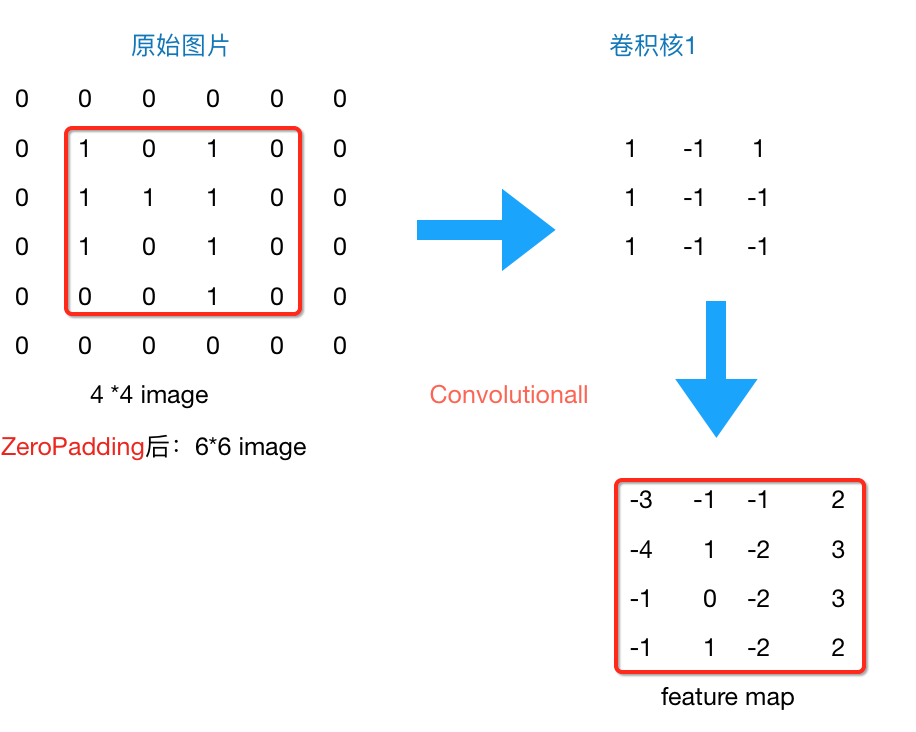
所以到现在为止,我们的图片由4*4,通过卷积层变为3*3,再通过池化层变化2*2,如果我们再添加层,那么图片岂不是会越变越小?这个时候我们就会引出“Zero Padding”(补零),它可以帮助我们保证每次经过卷积或池化输出后图片的大小不变,如,上述例子我们如果加入Zero Padding,再采用3*3的卷积核,那么变换后的图片尺寸与原图片尺寸相同,如下图所示:
|
||||
|
||||
|
||||

|
||||
|
||||
图4 zero padding结果
|
||||
|
||||
@@ -565,7 +565,7 @@ class LayerHelper(object):
|
||||
|
||||
到这一步,其实我们的一个完整的“卷积部分”就算完成了,如果想要叠加层数,一般也是叠加“Conv-MaxPooing",通过不断的设计卷积核的尺寸,数量,提取更多的特征,最后识别不同类别的物体。做完Max Pooling后,我们就会把这些数据“拍平”,丢到Flatten层,然后把Flatten层的output放到full connected Layer里,采用softmax对其进行分类。
|
||||
|
||||
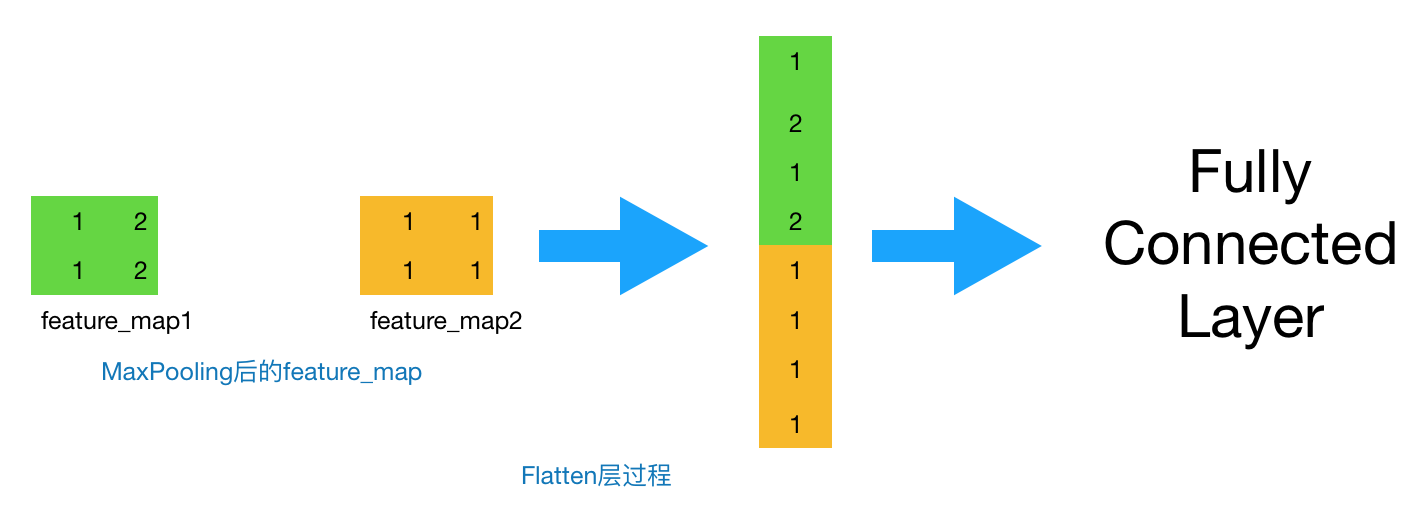
|
||||

|
||||
|
||||
图5 Flatten过程
|
||||
|
||||
@@ -586,7 +586,7 @@ class LayerHelper(object):
|
||||
1.卷积核的尺寸不一定非得为正方形。长方形也可以,只不过通常情况下为正方形。如果要设置为长方形,那么首先得保证这层的输出形状是整数,不能是小数。如果你的图像是边长为 28 的正方形。那么卷积层的输出就满足 [ (28 - kernel_size)/ stride ] + 1 ,这个数值得是整数才行,否则没有物理意义。譬如,你算得一个边长为 3.6 的 feature map 是没有物理意义的。 pooling 层同理。FC 层的输出形状总是满足整数,其唯一的要求就是整个训练过程中 FC 层的输入得是定长的。如果你的图像不是正方形。那么在制作数据时,可以缩放到统一大小(非正方形),再使用非正方形的 kernel_size 来使得卷积层的输出依然是整数。总之,撇开网络结果设定的好坏不谈,其本质上就是在做算术应用题: 如何使得各层的输出是整数。
|
||||
|
||||
|
||||
2.由经验确定。通常情况下,靠近输入的卷积层,譬如第一层卷积层,会找出一些共性的特征,如手写数字识别中第一层我们设定卷积核个数为5个,一般是找出诸如"横线"、“竖线”、“斜线”等共性特征,我们称之为basic feature,经过max pooling后,在第二层卷积层,设定卷积核个数为20个,可以找出一些相对复杂的特征,如“横折”、“左半圆”、“右半圆”等特征,越往后,卷积核设定的数目越多,越能体现label的特征就越细致,就越容易分类出来,打个比方,如果你想分类出“0”的数字,你看到这个特征,能推测是什么数字呢?只有越往后,检测识别的特征越多,试过能识别这几个特征,那么我就能够确定这个数字是“0”。
|
||||
2.由经验确定。通常情况下,靠近输入的卷积层,譬如第一层卷积层,会找出一些共性的特征,如手写数字识别中第一层我们设定卷积核个数为5个,一般是找出诸如"横线"、“竖线”、“斜线”等共性特征,我们称之为basic feature,经过max pooling后,在第二层卷积层,设定卷积核个数为20个,可以找出一些相对复杂的特征,如“横折”、“左半圆”、“右半圆”等特征,越往后,卷积核设定的数目越多,越能体现label的特征就越细致,就越容易分类出来,打个比方,如果你想分类出“0”的数字,你看到这个特征,能推测是什么数字呢?只有越往后,检测识别的特征越多,试过能识别这几个特征,那么我就能够确定这个数字是“0”。
|
||||
|
||||
|
||||
3.有stride_w和stride_h,后者表示的就是上下步长。如果用stride,则表示stride_h=stride_w=stride。
|
||||
@@ -632,7 +632,7 @@ def convolutional_neural_network_org(img):
|
||||
|
||||
那么这个时候我考虑的问题是,既然上面我们已经了解了卷积核,改变卷积核的大小是否会对我的结果造成影响?增多卷积核的数目能够提高准确率?于是我做了个实验:
|
||||
|
||||
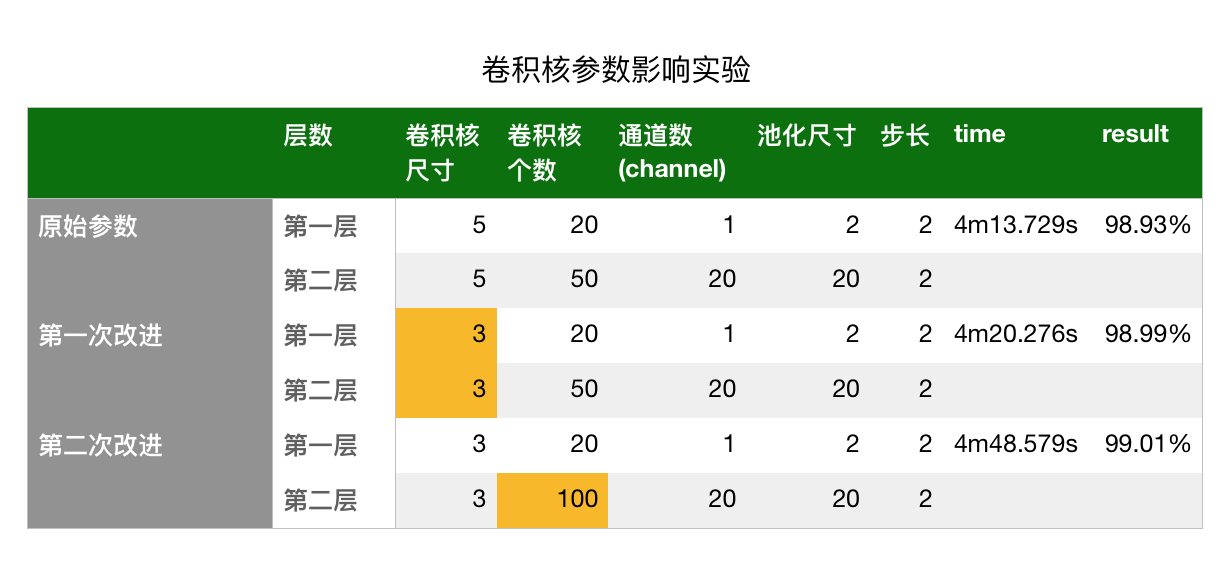
|
||||

|
||||
|
||||
* 第一次改进: 仅改变第一层与第二层的卷积核数目的大小,其他保持不变。可以看到结果提升了0.06%
|
||||
* 第二次改进: 保持3*3的卷积核大小,仅改变第二层的卷积核数目,其他保持不变,可以看到结果相较于原始参数提升了0.08%
|
||||
|
||||
@@ -4,35 +4,35 @@
|
||||
|
||||
**LSTM**(Long Short-Term Memory)长短期记忆网络,是一种时间递归神经网络,**适合于处理和预测时间序列中间隔和延迟相对较长的重要事件**。LSTM是解决循环神经网络RNN结构中存在的“梯度消失”问题而提出的,是一种特殊的循环神经网络。最常见的一个例子就是: 当我们要预测“the clouds are in the (...)"的时候, 这种情况下,相关的信息和预测的词位置之间的间隔很小,RNN会使用先前的信息预测出词是”sky“。但是如果想要预测”I grew up in France ... I speak fluent (...)”,语言模型推测下一个词可能是一种语言的名字,但是具体是什么语言,需要用到间隔很长的前文中France,在这种情况下,RNN因为“梯度消失”的问题,并不能利用间隔很长的信息,然而,LSTM在设计上明确避免了长期依赖的问题,这主要归功于LSTM精心设计的“门”结构(输入门、遗忘门和输出门)消除或者增加信息到细胞状态的能力,使得LSTM能够记住长期的信息。
|
||||
|
||||
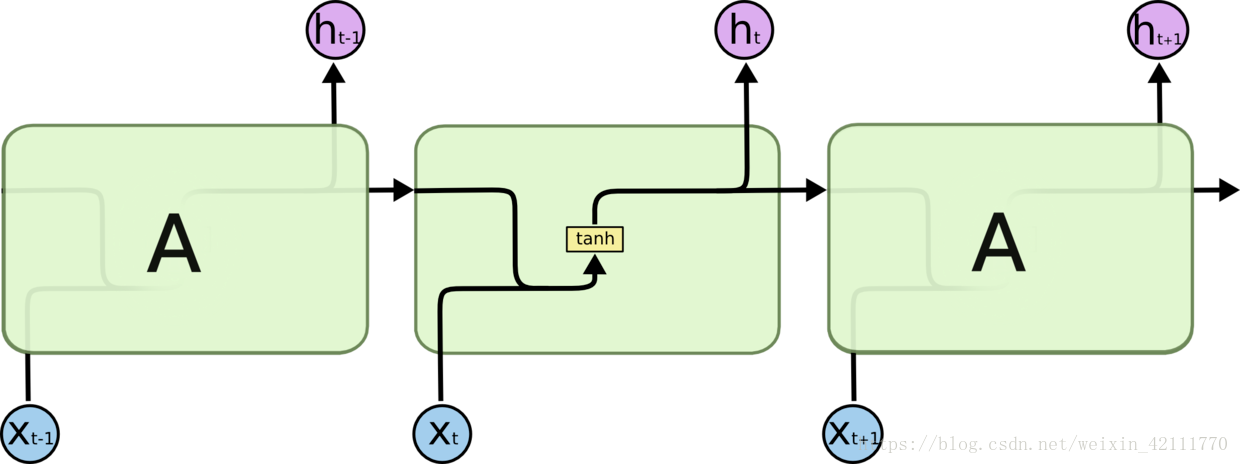 vs 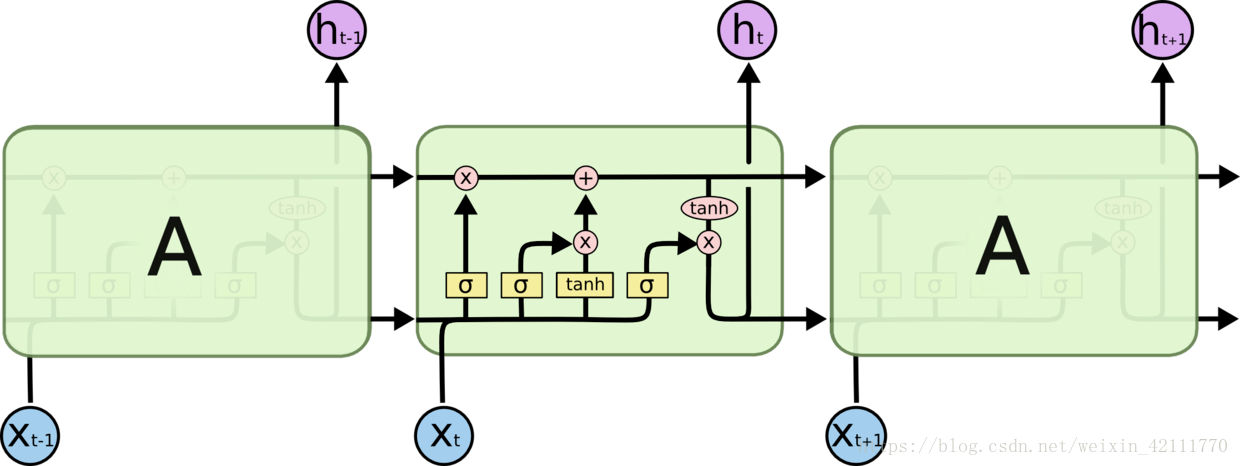
|
||||
 vs 
|
||||
|
||||
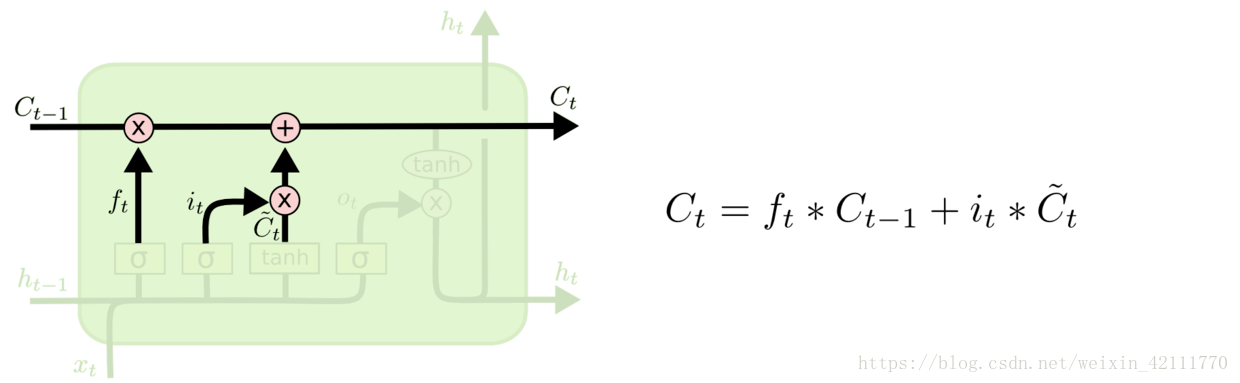
标准的RNN结构都具有一种重复神经网络模块的链式形式,一般是一个tanh层进行重复的学习(如上图左边图),而在LSTM中(上图右边图),重复的模块中有四个特殊的结构。**贯穿在图上方的水平线为细胞状态(cell),黄色的矩阵是学习得到的神经网络层,粉色的圆圈表示运算操作,黑色的箭头表示向量的传输**,整体看来,不仅仅是h在随着时间流动,细胞状态c也在随着时间流动,细胞状态c代表着长期记忆。
|
||||
|
||||
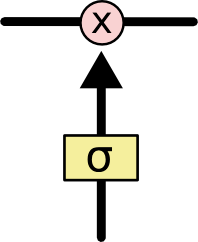
上面我们提到LSTM之所以能够记住长期的信息,在于设计的“门”结构,“门”结构是一种让信息选择式通过的方法,包括一个sigmoid神经网络层和一个pointwise乘法操作,如下图所示结构。复习一下sigmoid函数,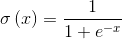,sigmoid输出为0到1之间的数组,一般用在二分类问题,输出值接近0代表“不允许通过”,趋向1代表“允许通过”。
|
||||
上面我们提到LSTM之所以能够记住长期的信息,在于设计的“门”结构,“门”结构是一种让信息选择式通过的方法,包括一个sigmoid神经网络层和一个pointwise乘法操作,如下图所示结构。复习一下sigmoid函数,,sigmoid输出为0到1之间的数组,一般用在二分类问题,输出值接近0代表“不允许通过”,趋向1代表“允许通过”。
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
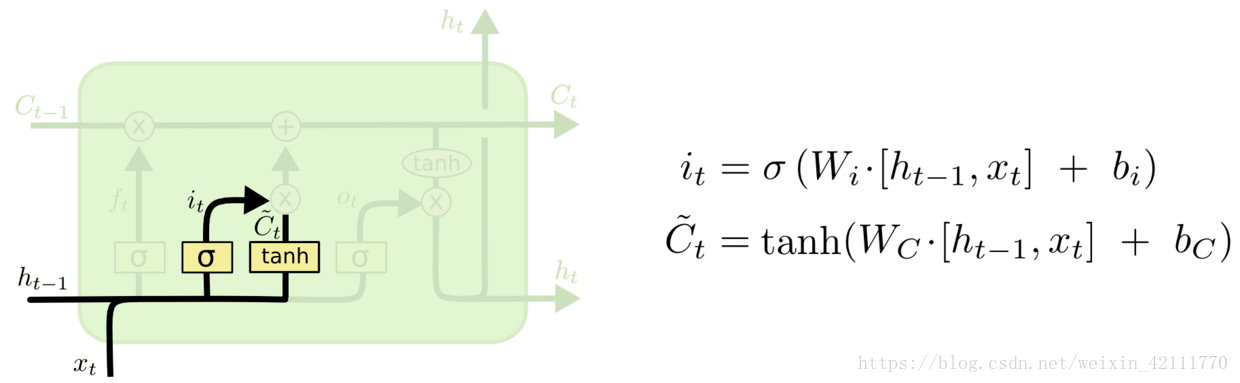
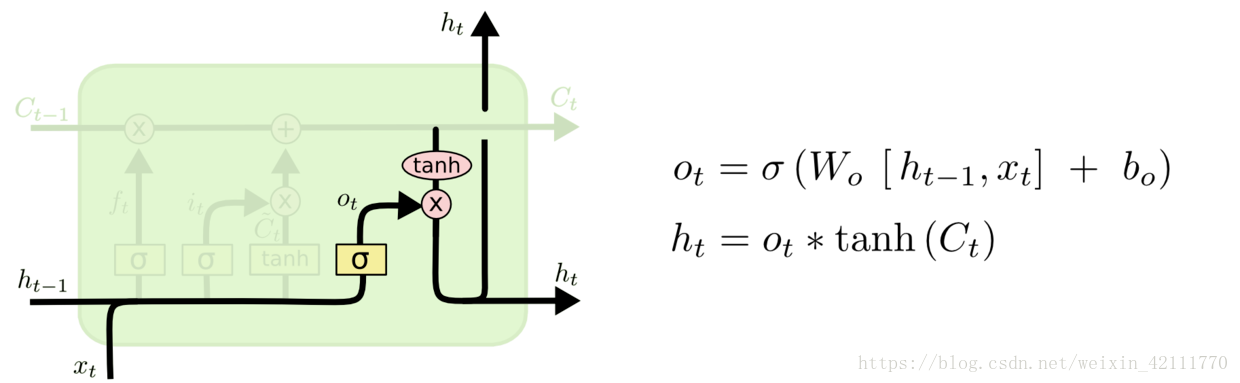
**在LSTM中,第一阶段是遗忘门,遗忘层决定哪些信息需要从细胞状态中被遗忘,下一阶段是输入门,输入门确定哪些新信息能够被存放到细胞状态中,最后一个阶段是输出门,输出门确定输出什么值**。下面我们把LSTM就着各个门的子结构和数学表达式进行分析。
|
||||
|
||||
* 遗忘门: 遗忘门是以上一层的输出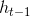和本层要输入的序列数据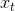作为输入,通过一个激活函数sigmoid,得到输出为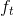。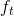的输出取值在[0,1]区间,表示上一层细胞状态被遗忘的概率,1是“完全保留”,0是“完全舍弃”
|
||||
* 遗忘门: 遗忘门是以上一层的输出和本层要输入的序列数据作为输入,通过一个激活函数sigmoid,得到输出为。的输出取值在[0,1]区间,表示上一层细胞状态被遗忘的概率,1是“完全保留”,0是“完全舍弃”
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
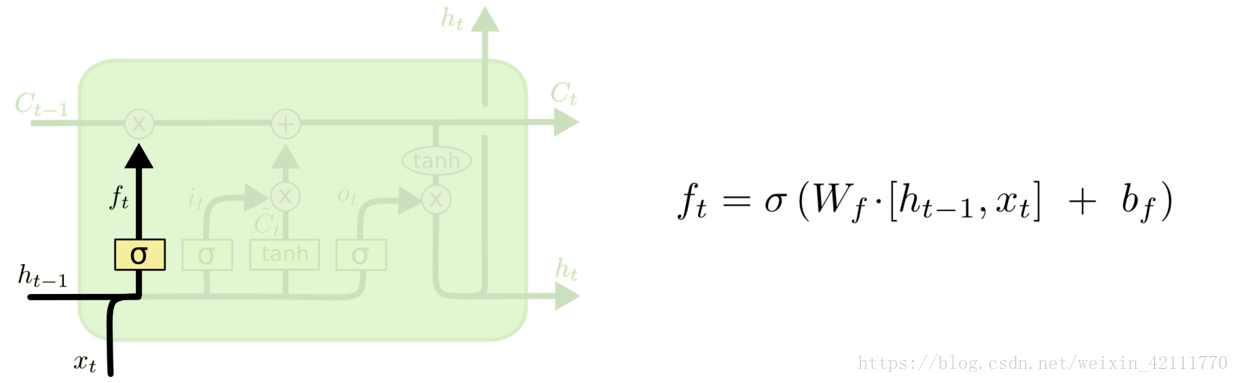
* 输入门: 输入门包含两个部分,第一部分使用sigmoid激活函数,输出为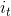,第二部分使用tanh激活函数,输出为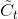。**【个人通俗理解: 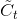在RNN网络中就是本层的输出,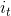是在[0,1]区间取值,表示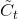中的信息被保留的程度,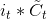表示该层被保留的新信息】**
|
||||
* 输入门: 输入门包含两个部分,第一部分使用sigmoid激活函数,输出为,第二部分使用tanh激活函数,输出为。**【个人通俗理解: 在RNN网络中就是本层的输出,是在[0,1]区间取值,表示中的信息被保留的程度,表示该层被保留的新信息】**
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
到目前为止,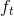是遗忘门的输出,控制着上一层细胞状态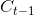被遗忘的程度,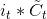为输入门的两个输出乘法运算,表示有多少新信息被保留,基于此,我们就可以把新信息更新这一层的细胞状态。
|
||||
到目前为止,是遗忘门的输出,控制着上一层细胞状态被遗忘的程度,为输入门的两个输出乘法运算,表示有多少新信息被保留,基于此,我们就可以把新信息更新这一层的细胞状态。
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
* 输出门: 输出门用来控制该层的细胞状态有多少被过滤。首先使用sigmoid激活函数得到一个[0,1]区间取值的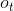,接着将细胞状态通过tanh激活函数处理后与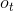相乘,即是本层的输出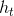。
|
||||
* 输出门: 输出门用来控制该层的细胞状态有多少被过滤。首先使用sigmoid激活函数得到一个[0,1]区间取值的,接着将细胞状态通过tanh激活函数处理后与相乘,即是本层的输出。
|
||||
|
||||
|
||||

|
||||
|
||||
|
||||
至此,终于将LSTM的结构理解了,现在有很多LSTM结构的变形,只要把这个母体结构理解了,再去理解变形的结构应该不会再有多麻烦了。
|
||||
@@ -41,21 +41,21 @@
|
||||
|
||||
双向RNN由两个普通的RNN所组成,一个正向的RNN,利用过去的信息,一个逆序的RNN,利用未来的信息,这样在时刻t,既能够使用t-1时刻的信息,又能够利用到t+1时刻的信息。一般来说,由于双向LSTM能够同时利用过去时刻和未来时刻的信息,会比单向LSTM最终的预测更加准确。下图为双向LSTM的结构。
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
* 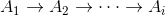为正向的RNN,参与正向计算,t时刻的输入为t时刻的序列数据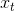和t-1时刻的输出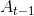
|
||||
* 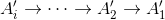为逆向的RNN,参与反向计算,t时刻的输入为t时刻的序列数据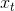和t+1时刻的输出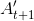
|
||||
* t时刻的最终输出值取决于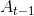和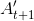
|
||||
* 为正向的RNN,参与正向计算,t时刻的输入为t时刻的序列数据和t-1时刻的输出
|
||||
* 为逆向的RNN,参与反向计算,t时刻的输入为t时刻的序列数据和t+1时刻的输出
|
||||
* t时刻的最终输出值取决于和
|
||||
|
||||
**GRU(Gated Recurrent Unit)**是LSTM最流行的一个变体,比LSTM模型要简单
|
||||
|
||||

|
||||

|
||||
|
||||
|
||||
GRU包括两个门,一个重置门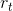和更新门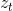。这两个门的激活函数为sigmoid函数,在[0,1]区间取值。
|
||||
GRU包括两个门,一个重置门和更新门。这两个门的激活函数为sigmoid函数,在[0,1]区间取值。
|
||||
|
||||
候选隐含状态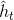使用重置门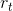来控制t-1时刻信息的输入,如果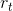结果为0,那么上一个隐含状态的输出信息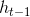将被丢弃。也就是说,**重置门决定过去有多少信息被遗忘,有助于捕捉时序数据中短期的依赖关系**。
|
||||
候选隐含状态使用重置门来控制t-1时刻信息的输入,如果结果为0,那么上一个隐含状态的输出信息将被丢弃。也就是说,**重置门决定过去有多少信息被遗忘,有助于捕捉时序数据中短期的依赖关系**。
|
||||
|
||||
|
||||
隐含状态使用更新门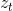对上一时刻隐含状态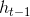和候选隐含状态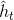进行更新。更新门控制过去的隐含状态在当前时刻的重要性,**如果更新门一直趋近于1,t时刻之前的隐含状态将一直保存下来并全传递到t时刻,****更新门有助于捕捉时序数据中中长期的依赖关系**。
|
||||
隐含状态使用更新门对上一时刻隐含状态和候选隐含状态进行更新。更新门控制过去的隐含状态在当前时刻的重要性,**如果更新门一直趋近于1,t时刻之前的隐含状态将一直保存下来并全传递到t时刻,****更新门有助于捕捉时序数据中中长期的依赖关系**。
|
||||
|
||||
@@ -7,7 +7,7 @@
|
||||
循环神经网络的应用场景比较多,比如暂时能写论文,写程序,写诗,但是,(总是会有但是的),但是他们现在还不能正常使用,学习出来的东西没有逻辑,所以要想真正让它更有用,路还很远。
|
||||
|
||||
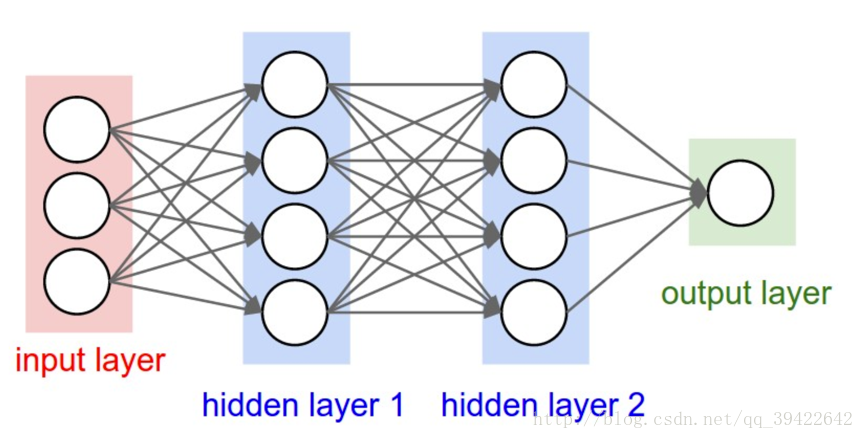
这是一般的神经网络应该有的结构:
|
||||
|
||||

|
||||
|
||||
既然我们已经有了人工神经网络和卷积神经网络,为什么还要循环神经网络?
|
||||
原因很简单,无论是卷积神经网络,还是人工神经网络,他们的前提假设都是: 元素之间是相互独立的,**输入与输出也是独立的**,比如猫和狗。
|
||||
@@ -16,18 +16,18 @@
|
||||
## 2.RNN的网络结构及原理
|
||||
|
||||
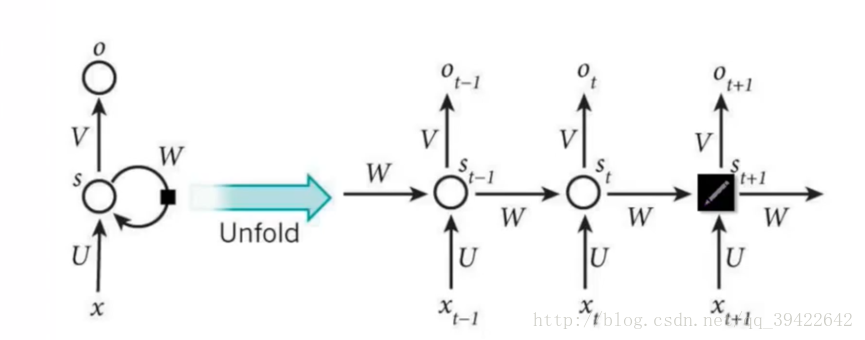
它的网络结构如下:
|
||||
|
||||

|
||||
其中每个圆圈可以看作是一个单元,而且每个单元做的事情也是一样的,因此可以折叠呈左半图的样子。用一句话解释RNN,就是**一个单元结构重复使用**。
|
||||
|
||||
RNN是一个序列到序列的模型,假设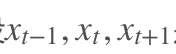是一个输入: “我是中国“,那么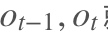就应该对应”是”,”中国”这两个,预测下一个词最有可能是什么?就是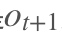应该是”人”的概率比较大。
|
||||
RNN是一个序列到序列的模型,假设是一个输入: “我是中国“,那么就应该对应”是”,”中国”这两个,预测下一个词最有可能是什么?就是应该是”人”的概率比较大。
|
||||
|
||||
因此,我们可以做这样的定义:
|
||||
|
||||

|
||||

|
||||
|
||||
。因为我们当前时刻的输出是由记忆和当前时刻的输入决定的,就像你现在大四,你的知识是由大四学到的知识(当前输入)和大三以及大三以前学到的东西的(记忆)的结合,RNN在这点上也类似,神经网络最擅长做的就是通过一系列参数把很多内容整合到一起,然后学习这个参数,因此就定义了RNN的基础:
|
||||
|
||||
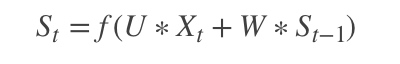
|
||||

|
||||
|
||||
大家可能会很好奇,为什么还要加一个f()函数,其实这个函数是神经网络中的激活函数,但为什么要加上它呢?
|
||||
举个例子,假如你在大学学了非常好的解题方法,那你初中那时候的解题方法还要用吗?显然是不用了的。RNN的想法也一样,既然我能记忆了,那我当然是只记重要的信息啦,其他不重要的,就肯定会忘记,是吧。但是在神经网络中什么最适合过滤信息呀?肯定是激活函数嘛,因此在这里就套用一个激活函数,来做一个非线性映射,来过滤信息,这个激活函数可能为tanh,也可为其他。
|
||||
@@ -35,10 +35,10 @@ RNN是一个序列到序列的模型,假设
|
||||

|
||||
|
||||
|
||||
其中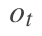就表示时刻t的输出。
|
||||
其中就表示时刻t的输出。
|
||||
|
||||
RNN中的结构细节:
|
||||
1.可以把St当作隐状态,捕捉了之前时间点上的信息。就像你去考研一样,考的时候记住了你能记住的所有信息。
|
||||
@@ -50,10 +50,10 @@ RNN中的结构细节:
|
||||
## 3.RNN的改进1: 双向RNN
|
||||
|
||||
在有些情况,比如有一部电视剧,在第三集的时候才出现的人物,现在让预测一下在第三集中出现的人物名字,你用前面两集的内容是预测不出来的,所以你需要用到第四,第五集的内容来预测第三集的内容,这就是双向RNN的想法。如图是双向RNN的图解:
|
||||
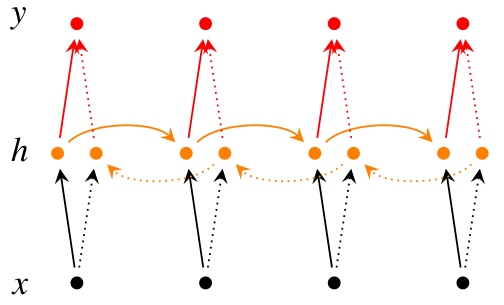
|
||||
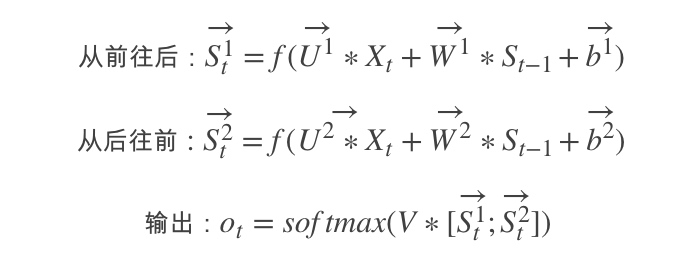
|
||||

|
||||

|
||||
|
||||
这里的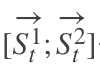做的是一个拼接,如果他们都是1000x1维的,拼接在一起就是1000x2维的了。
|
||||
这里的做的是一个拼接,如果他们都是1000x1维的,拼接在一起就是1000x2维的了。
|
||||
|
||||
双向RNN需要的内存是单向RNN的两倍,因为在同一时间点,双向RNN需要保存两个方向上的权重参数,在分类的时候,需要同时输入两个隐藏层输出的信息。
|
||||
|
||||
@@ -61,18 +61,18 @@ RNN中的结构细节:
|
||||
|
||||
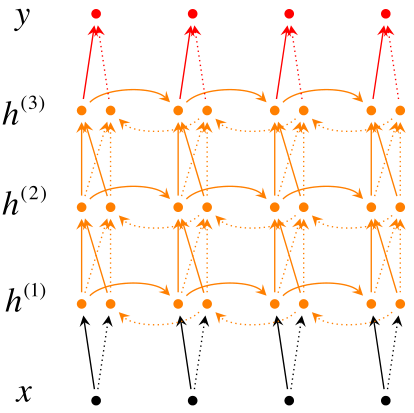
深层双向RNN 与双向RNN相比,多了几个隐藏层,因为他的想法是很多信息记一次记不下来,比如你去考研,复习考研英语的时候,背英语单词一定不会就看一次就记住了所有要考的考研单词吧,你应该也是带着先前几次背过的单词,然后选择那些背过,但不熟的内容,或者没背过的单词来背吧。
|
||||
|
||||
深层双向RNN就是基于这么一个想法,他的输入有两方面,第一就是前一时刻的隐藏层传过来的信息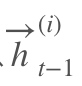,和当前时刻上一隐藏层传过来的信息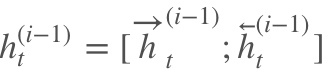,包括前向和后向的。
|
||||
|
||||
深层双向RNN就是基于这么一个想法,他的输入有两方面,第一就是前一时刻的隐藏层传过来的信息,和当前时刻上一隐藏层传过来的信息,包括前向和后向的。
|
||||

|
||||
|
||||
我们用公式来表示是这样的:
|
||||
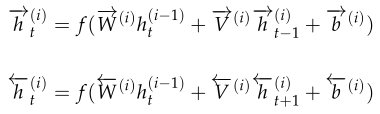
|
||||

|
||||
然后再利用最后一层来进行分类,分类公式如下:
|
||||
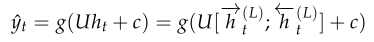
|
||||

|
||||
|
||||
### 4.1 Pyramidal RNN
|
||||
|
||||
其他类似的网络还有Pyramidal RNN:
|
||||
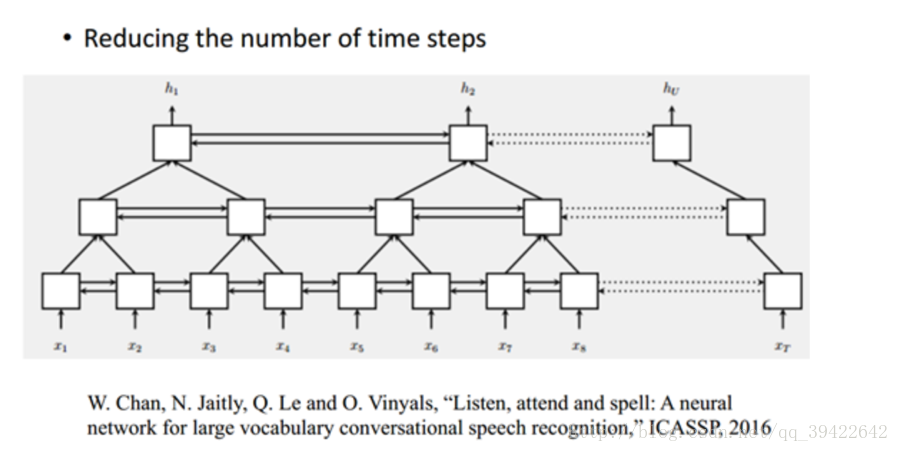
|
||||

|
||||
我们现在有一个很长的输入序列,可以看到这是一个双向的RNN,上图是谷歌的W.Chan做的一个测试,它原先要做的是语音识别,他要用序列到序列的模型做语音识别,序列到序列就是说,输入一个序列然后就输出一个序列。
|
||||
|
||||
由图我们发现,上一层的两个输出,作为当前层的输入,如果是非常长的序列的话,这样做的话,每一层的序列都比上一层要短,但当前层的输入f(x)也会随之增多,貌似看一起相互抵消,运算量并没有什么改进。
|
||||
@@ -84,55 +84,55 @@ RNN中的结构细节:
|
||||
|
||||
如前面我们讲的,如果要预测t时刻的输出,我们必须先利用上一时刻(t-1)的记忆和当前时刻的输入,得到t时刻的记忆:
|
||||
|
||||
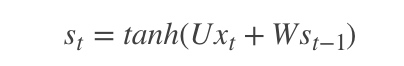
|
||||

|
||||
|
||||
然后利用当前时刻的记忆,通过softmax分类器输出每个词出现的概率:
|
||||
|
||||
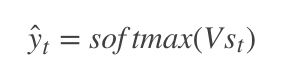
|
||||

|
||||
|
||||
为了找出模型最好的参数,U,W,V,我们就要知道当前参数得到的结果怎么样,因此就要定义我们的损失函数,用交叉熵损失函数:
|
||||
|
||||
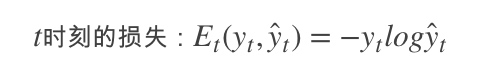
|
||||

|
||||
|
||||
其中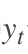
|
||||
t时刻的标准答案,是一个只有一个是1,其他都是0的向量; 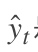是我们预测出来的结果,与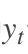
|
||||
其中
|
||||
t时刻的标准答案,是一个只有一个是1,其他都是0的向量; 是我们预测出来的结果,与
|
||||
的维度一样,但它是一个概率向量,里面是每个词出现的概率。因为对结果的影响,肯定不止一个时刻,因此需要把所有时刻的造成的损失都加起来:
|
||||
|
||||
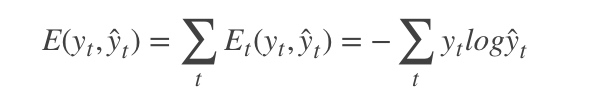
|
||||

|
||||
|
||||
|
||||

|
||||
|
||||
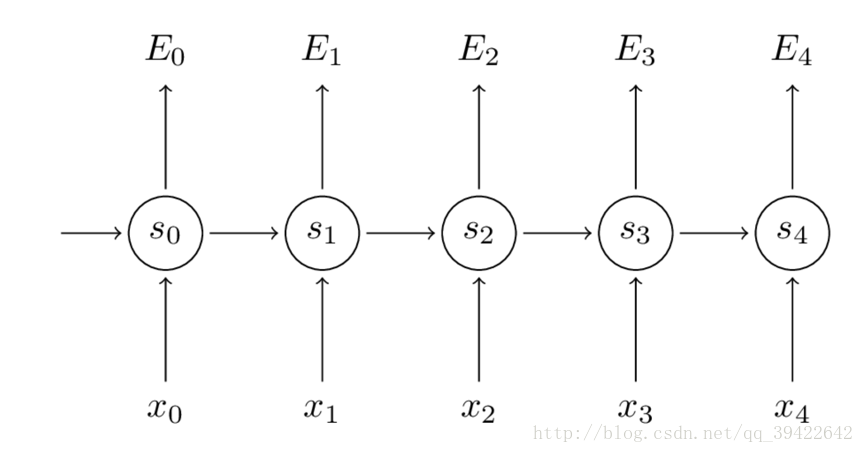
如图所示,你会发现每个cell都会有一个损失,我们已经定义好了损失函数,接下来就是熟悉的一步了,那就是根据损失函数利用SGD来求解最优参数,在CNN中使用反向传播BP算法来求解最优参数,但在RNN就要用到BPTT,它和BP算法的本质区别,也是CNN和RNN的本质区别: CNN没有记忆功能,它的输出仅依赖与输入,但RNN有记忆功能,它的输出不仅依赖与当前输入,还依赖与当前的记忆。这个记忆是序列到序列的,也就是当前时刻收到上一时刻的影响,比如股市的变化。
|
||||
|
||||
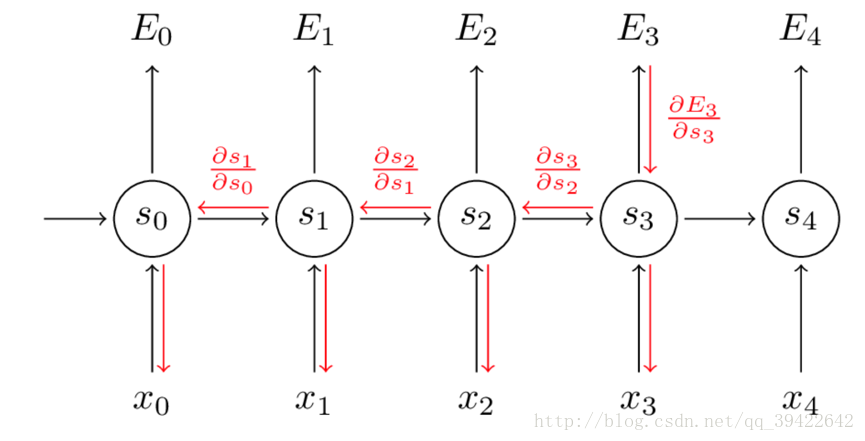
因此,在对参数求偏导的时候,对当前时刻求偏导,一定会涉及前一时刻,我们用例子看一下:
|
||||
|
||||
|
||||

|
||||
|
||||
假设我们对E3的W求偏导: 它的损失首先来源于预测的输出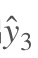
|
||||
,预测的输出又是来源于当前时刻的记忆s3,当前的记忆又是来源于当前的输出和截止到上一时刻的记忆: 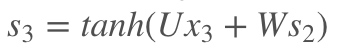
|
||||
假设我们对E3的W求偏导: 它的损失首先来源于预测的输出
|
||||
,预测的输出又是来源于当前时刻的记忆s3,当前的记忆又是来源于当前的输出和截止到上一时刻的记忆: 
|
||||
因此,根据链式法则可以有:
|
||||
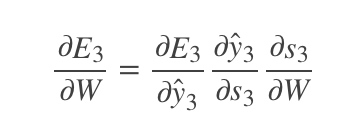
|
||||

|
||||
|
||||
但是,你会发现,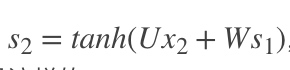
|
||||
但是,你会发现,
|
||||
,也就是s2里面的函数还包含了W,因此,这个链式法则还没到底,就像图上画的那样,所以真正的链式法则是这样的:
|
||||
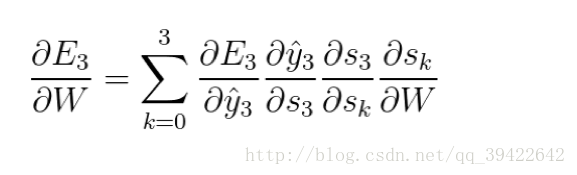
|
||||

|
||||
我们要把当前时刻造成的损失,和以往每个时刻造成的损失加起来,因为我们每一个时刻都用到了权重参数W。和以往的网络不同,一般的网络,比如人工神经网络,参数是不同享的,但在循环神经网络,和CNN一样,设立了参数共享机制,来降低模型的计算量。
|
||||
|
||||
## 6.RNN与CNN的结合应用: 看图说话
|
||||
|
||||
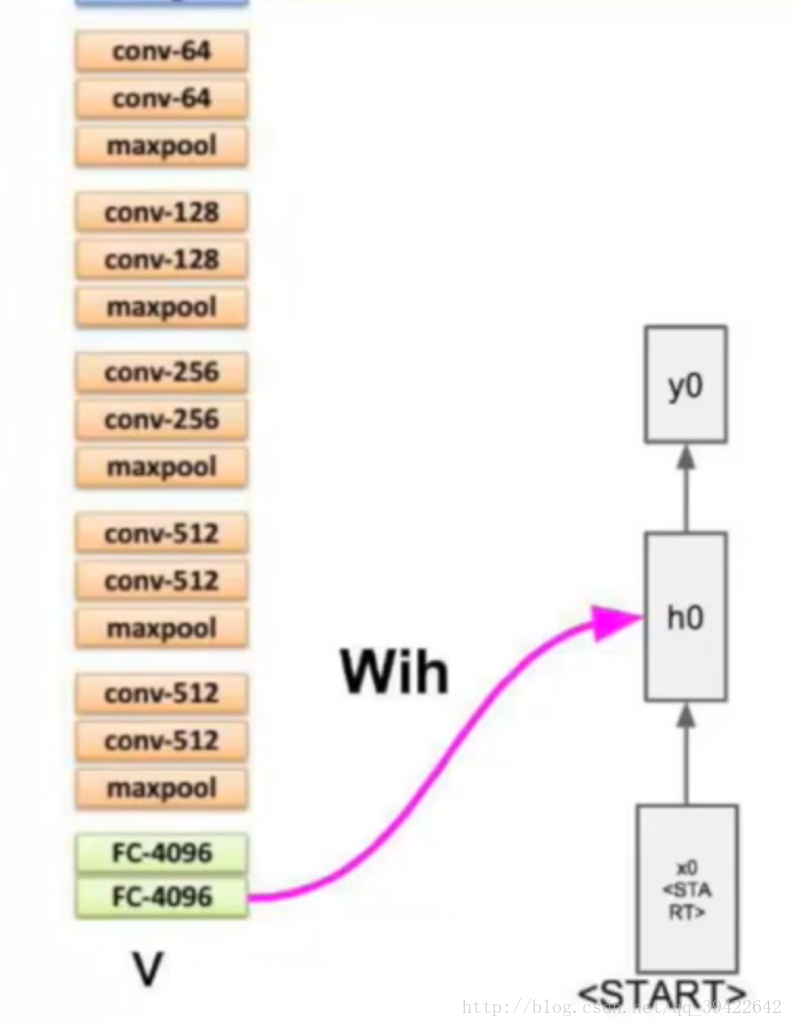
在图像处理中,目前做的最好的是CNN,而自然语言处理中,表现比较好的是RNN,因此,我们能否把他们结合起来,一起用呢?那就是看图说话了,这个原理也比较简单,举个小栗子: 假设我们有CNN的模型训练了一个网络结构,比如是这个
|
||||
|
||||
|
||||

|
||||
|
||||
最后我们不是要分类嘛,那在分类前,是不是已经拿到了图像的特征呀,那我们能不能把图像的特征拿出来,放到RNN的输入里,让他学习呢?
|
||||
|
||||
之前的RNN是这样的:
|
||||
|
||||
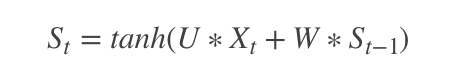
|
||||

|
||||
|
||||
我们把图像的特征加在里面,可以得到:
|
||||
|
||||
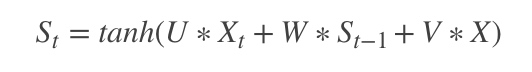
|
||||

|
||||
|
||||
其中的X就是图像的特征。如果用的是上面的CNN网络,X应该是一个4096X1的向量。
|
||||
|
||||
|
||||
BIN
docs/dl/img/CNN原理/853467-20171031123650574-11330636.png
Normal file
|
After Width: | Height: | Size: 80 KiB |
BIN
docs/dl/img/CNN原理/853467-20171031215017701-495180034.png
Normal file
|
After Width: | Height: | Size: 7.5 KiB |
BIN
docs/dl/img/CNN原理/853467-20171031231438107-1902818098.png
Normal file
|
After Width: | Height: | Size: 411 B |
BIN
docs/dl/img/CNN原理/853467-20171031232805748-157396975.png
Normal file
|
After Width: | Height: | Size: 16 KiB |
BIN
docs/dl/img/CNN原理/853467-20171101085737623-1572944193.png
Normal file
|
After Width: | Height: | Size: 1.0 KiB |
BIN
docs/dl/img/CNN原理/853467-20171104142033154-1330878114.png
Normal file
|
After Width: | Height: | Size: 8.0 KiB |
BIN
docs/dl/img/CNN原理/853467-20171104142056685-2048616836.png
Normal file
|
After Width: | Height: | Size: 6.3 KiB |
BIN
docs/dl/img/CNN原理/853467-20171104142200763-1912037434.png
Normal file
|
After Width: | Height: | Size: 7.2 KiB |
BIN
docs/dl/img/LSTM原理/20180704173230785.jpg
Normal file
|
After Width: | Height: | Size: 12 KiB |
BIN
docs/dl/img/LSTM原理/20180704173253439.jpg
Normal file
|
After Width: | Height: | Size: 8.9 KiB |
BIN
docs/dl/img/LSTM原理/20180705152515679.jpg
Normal file
|
After Width: | Height: | Size: 1.0 KiB |
BIN
docs/dl/img/LSTM原理/20180705153027598.jpg
Normal file
|
After Width: | Height: | Size: 423 B |
BIN
docs/dl/img/LSTM原理/20180705154117297.jpg
Normal file
|
After Width: | Height: | Size: 8.3 KiB |
BIN
docs/dl/img/LSTM原理/20180705154140100.jpg
Normal file
|
After Width: | Height: | Size: 11 KiB |
BIN
docs/dl/img/LSTM原理/20180705154157781.jpg
Normal file
|
After Width: | Height: | Size: 8.2 KiB |
BIN
docs/dl/img/LSTM原理/20180705154210768.jpg
Normal file
|
After Width: | Height: | Size: 10 KiB |
BIN
docs/dl/img/LSTM原理/20180705154943659.jpg
Normal file
|
After Width: | Height: | Size: 238 B |
BIN
docs/dl/img/LSTM原理/20180705155022656.jpg
Normal file
|
After Width: | Height: | Size: 194 B |
BIN
docs/dl/img/LSTM原理/201807051551130.jpg
Normal file
|
After Width: | Height: | Size: 207 B |
BIN
docs/dl/img/LSTM原理/20180705155135748.jpg
Normal file
|
After Width: | Height: | Size: 207 B |
BIN
docs/dl/img/LSTM原理/20180705160829424.jpg
Normal file
|
After Width: | Height: | Size: 191 B |
BIN
docs/dl/img/LSTM原理/20180705161911316.jpg
Normal file
|
After Width: | Height: | Size: 232 B |
BIN
docs/dl/img/LSTM原理/20180705162106120.jpg
Normal file
|
After Width: | Height: | Size: 232 B |
BIN
docs/dl/img/LSTM原理/20180705162239540.jpg
Normal file
|
After Width: | Height: | Size: 191 B |
BIN
docs/dl/img/LSTM原理/20180705162518689.jpg
Normal file
|
After Width: | Height: | Size: 309 B |
BIN
docs/dl/img/LSTM原理/20180705162835994.jpg
Normal file
|
After Width: | Height: | Size: 232 B |
BIN
docs/dl/img/LSTM原理/20180705162951402.jpg
Normal file
|
After Width: | Height: | Size: 207 B |
BIN
docs/dl/img/LSTM原理/20180705163019968.jpg
Normal file
|
After Width: | Height: | Size: 245 B |
BIN
docs/dl/img/LSTM原理/20180705163047274.jpg
Normal file
|
After Width: | Height: | Size: 309 B |
BIN
docs/dl/img/LSTM原理/20180705163146715.jpg
Normal file
|
After Width: | Height: | Size: 218 B |
BIN
docs/dl/img/LSTM原理/20180705163549770.jpg
Normal file
|
After Width: | Height: | Size: 191 B |
BIN
docs/dl/img/LSTM原理/20180705164009353.jpg
Normal file
|
After Width: | Height: | Size: 218 B |
BIN
docs/dl/img/LSTM原理/20180705164029948.jpg
Normal file
|
After Width: | Height: | Size: 191 B |
BIN
docs/dl/img/LSTM原理/20180705164102617.jpg
Normal file
|
After Width: | Height: | Size: 205 B |
BIN
docs/dl/img/LSTM原理/20180713200802779.jpg
Normal file
|
After Width: | Height: | Size: 14 KiB |
BIN
docs/dl/img/LSTM原理/20180713200829571.jpg
Normal file
|
After Width: | Height: | Size: 20 KiB |
BIN
docs/dl/img/LSTM原理/20180713204707320.jpg
Normal file
|
After Width: | Height: | Size: 434 B |
BIN
docs/dl/img/LSTM原理/20180713204802532.jpg
Normal file
|
After Width: | Height: | Size: 465 B |
BIN
docs/dl/img/LSTM原理/20180713204825347.jpg
Normal file
|
After Width: | Height: | Size: 268 B |
BIN
docs/dl/img/LSTM原理/20180713204838867.jpg
Normal file
|
After Width: | Height: | Size: 241 B |
BIN
docs/dl/img/LSTM原理/20180713204850377.jpg
Normal file
|
After Width: | Height: | Size: 194 B |
BIN
docs/dl/img/LSTM原理/20180713204852425.jpg
Normal file
|
After Width: | Height: | Size: 194 B |
BIN
docs/dl/img/LSTM原理/20180713204913638.jpg
Normal file
|
After Width: | Height: | Size: 268 B |
BIN
docs/dl/img/LSTM原理/20180713205653854.jpg
Normal file
|
After Width: | Height: | Size: 188 B |
BIN
docs/dl/img/LSTM原理/20180713205710503.jpg
Normal file
|
After Width: | Height: | Size: 190 B |
BIN
docs/dl/img/LSTM原理/20180713210203944.jpg
Normal file
|
After Width: | Height: | Size: 220 B |
BIN
docs/dl/img/LSTM原理/20180713210738834.jpg
Normal file
|
After Width: | Height: | Size: 238 B |
BIN
docs/dl/img/LSTM原理/20180713211322965.jpg
Normal file
|
After Width: | Height: | Size: 238 B |
BIN
docs/dl/img/RNN原理/15570321772488.jpg
Normal file
|
After Width: | Height: | Size: 766 B |
BIN
docs/dl/img/RNN原理/15570322195709.jpg
Normal file
|
After Width: | Height: | Size: 554 B |
BIN
docs/dl/img/RNN原理/15570322451341.jpg
Normal file
|
After Width: | Height: | Size: 379 B |
BIN
docs/dl/img/RNN原理/15570322822857.jpg
Normal file
|
After Width: | Height: | Size: 3.5 KiB |
BIN
docs/dl/img/RNN原理/15570322981095.jpg
Normal file
|
After Width: | Height: | Size: 1.4 KiB |
BIN
docs/dl/img/RNN原理/15570323546017.jpg
Normal file
|
After Width: | Height: | Size: 1.2 KiB |
BIN
docs/dl/img/RNN原理/15570323768890.jpg
Normal file
|
After Width: | Height: | Size: 283 B |
BIN
docs/dl/img/RNN原理/15570324711246.jpg
Normal file
|
After Width: | Height: | Size: 6.7 KiB |
BIN
docs/dl/img/RNN原理/15570324937386.jpg
Normal file
|
After Width: | Height: | Size: 748 B |
BIN
docs/dl/img/RNN原理/15570325271812.jpg
Normal file
|
After Width: | Height: | Size: 800 B |
BIN
docs/dl/img/RNN原理/15570325458791.jpg
Normal file
|
After Width: | Height: | Size: 2.7 KiB |
BIN
docs/dl/img/RNN原理/15570325921406.jpg
Normal file
|
After Width: | Height: | Size: 1.3 KiB |
BIN
docs/dl/img/RNN原理/15570326059642.jpg
Normal file
|
After Width: | Height: | Size: 1.2 KiB |
BIN
docs/dl/img/RNN原理/15570326336949.jpg
Normal file
|
After Width: | Height: | Size: 2.0 KiB |
BIN
docs/dl/img/RNN原理/15570326727679.jpg
Normal file
|
After Width: | Height: | Size: 348 B |
BIN
docs/dl/img/RNN原理/15570326853547.jpg
Normal file
|
After Width: | Height: | Size: 379 B |
BIN
docs/dl/img/RNN原理/15570327422935.jpg
Normal file
|
After Width: | Height: | Size: 296 B |
BIN
docs/dl/img/RNN原理/15570327570018.jpg
Normal file
|
After Width: | Height: | Size: 3.4 KiB |
BIN
docs/dl/img/RNN原理/15570327881131.jpg
Normal file
|
After Width: | Height: | Size: 385 B |
BIN
docs/dl/img/RNN原理/15570328132196.jpg
Normal file
|
After Width: | Height: | Size: 1.5 KiB |
BIN
docs/dl/img/RNN原理/15570328255432.jpg
Normal file
|
After Width: | Height: | Size: 2.1 KiB |
BIN
docs/dl/img/RNN原理/15570328436386.jpg
Normal file
|
After Width: | Height: | Size: 1.3 KiB |
BIN
docs/dl/img/RNN原理/15570328705596.jpg
Normal file
|
After Width: | Height: | Size: 1.6 KiB |
BIN
docs/dl/img/RNN原理/15570328817086.jpg
Normal file
|
After Width: | Height: | Size: 1.9 KiB |
BIN
docs/dl/img/RNN原理/20171119130251741.jpg
Normal file
|
After Width: | Height: | Size: 19 KiB |
BIN
docs/dl/img/RNN原理/20171129184524844.jpg
Normal file
|
After Width: | Height: | Size: 12 KiB |
BIN
docs/dl/img/RNN原理/20171129213601819.jpg
Normal file
|
After Width: | Height: | Size: 42 KiB |
BIN
docs/dl/img/RNN原理/20171130091040277.jpg
Normal file
|
After Width: | Height: | Size: 8.0 KiB |
BIN
docs/dl/img/RNN原理/20171130091956686.jpg
Normal file
|
After Width: | Height: | Size: 8.8 KiB |
BIN
docs/dl/img/RNN原理/20171130094236429.jpg
Normal file
|
After Width: | Height: | Size: 5.0 KiB |
BIN
docs/dl/img/RNN原理/20171221152506461.jpg
Normal file
|
After Width: | Height: | Size: 22 KiB |
BIN
docs/dl/img/RNN原理/bi-directional-rnn.png
Normal file
|
After Width: | Height: | Size: 4.4 KiB |
BIN
docs/dl/img/RNN原理/deep-bi-directional-rnn-classification.png
Normal file
|
After Width: | Height: | Size: 1.3 KiB |
BIN
docs/dl/img/RNN原理/deep-bi-directional-rnn-hidden-layer.png
Normal file
|
After Width: | Height: | Size: 3.0 KiB |
BIN
docs/dl/img/RNN原理/deep-bi-directional-rnn.png
Normal file
|
After Width: | Height: | Size: 8.6 KiB |
BIN
docs/dl/img/反向传递/853467-20160630140644406-409859737.png
Normal file
|
After Width: | Height: | Size: 23 KiB |
BIN
docs/dl/img/反向传递/853467-20160630141449671-1058672778.png
Normal file
|
After Width: | Height: | Size: 19 KiB |
BIN
docs/dl/img/反向传递/853467-20160630142019140-402363317.png
Normal file
|
After Width: | Height: | Size: 21 KiB |
BIN
docs/dl/img/反向传递/853467-20160630142915359-294460310.png
Normal file
|
After Width: | Height: | Size: 4.3 KiB |
BIN
docs/dl/img/反向传递/853467-20160630150115390-1035378028.png
Normal file
|
After Width: | Height: | Size: 2.2 KiB |
BIN
docs/dl/img/反向传递/853467-20160630150244265-1128303244.png
Normal file
|
After Width: | Height: | Size: 1.6 KiB |
BIN
docs/dl/img/反向传递/853467-20160630150517109-389457135.png
Normal file
|
After Width: | Height: | Size: 8.4 KiB |
BIN
docs/dl/img/反向传递/853467-20160630150638390-1210364296.png
Normal file
|
After Width: | Height: | Size: 1.5 KiB |
BIN
docs/dl/img/反向传递/853467-20160630151201812-1014280864.png
Normal file
|
After Width: | Height: | Size: 2.0 KiB |
BIN
docs/dl/img/反向传递/853467-20160630151457593-1250510503.png
Normal file
|
After Width: | Height: | Size: 4.2 KiB |
BIN
docs/dl/img/反向传递/853467-20160630151508999-1967746600.png
Normal file
|
After Width: | Height: | Size: 1.5 KiB |
BIN
docs/dl/img/反向传递/853467-20160630151516093-1257166735.png
Normal file
|
After Width: | Height: | Size: 3.9 KiB |
BIN
docs/dl/img/反向传递/853467-20160630151916796-1001638091.png
Normal file
|
After Width: | Height: | Size: 4.4 KiB |
BIN
docs/dl/img/反向传递/853467-20160630152018906-1524325812.png
Normal file
|
After Width: | Height: | Size: 14 KiB |