mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2026-02-02 18:39:09 +08:00
293 lines
9.9 KiB
Markdown
293 lines
9.9 KiB
Markdown
<p align="center">
|
||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ" target="_blank">
|
||
<img src="https://code-thinking-1253855093.file.myqcloud.com/pics/20210924105952.png" width="1000"/>
|
||
</a>
|
||
<p align="center"><strong><a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
## 309.最佳买卖股票时机含冷冻期
|
||
|
||
[力扣题目链接](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/)
|
||
|
||
[https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/](https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock-with-cooldown/)
|
||
|
||
给定一个整数数组,其中第 i 个元素代表了第 i 天的股票价格 。
|
||
|
||
设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票):
|
||
|
||
* 你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
|
||
* 卖出股票后,你无法在第二天买入股票 (即冷冻期为 1 天)。
|
||
|
||
示例:
|
||
输入: [1,2,3,0,2]
|
||
输出: 3
|
||
解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]
|
||
|
||
|
||
## 思路
|
||
|
||
|
||
相对于[动态规划:122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II(动态规划).html),本题加上了一个冷冻期
|
||
|
||
|
||
在[动态规划:122.买卖股票的最佳时机II](https://programmercarl.com/0122.买卖股票的最佳时机II(动态规划).html) 中有两个状态,持有股票后的最多现金,和不持有股票的最多现金。
|
||
|
||
动规五部曲,分析如下:
|
||
|
||
1. 确定dp数组以及下标的含义
|
||
|
||
dp[i][j],第i天状态为j,所剩的最多现金为dp[i][j]。
|
||
|
||
**其实本题很多同学搞的比较懵,是因为出现冷冻期之后,状态其实是比较复杂度**,例如今天买入股票、今天卖出股票、今天是冷冻期,都是不能操作股票的。
|
||
具体可以区分出如下四个状态:
|
||
|
||
* 状态一:买入股票状态(今天买入股票,或者是之前就买入了股票然后没有操作)
|
||
* 卖出股票状态,这里就有两种卖出股票状态
|
||
* 状态二:两天前就卖出了股票,度过了冷冻期,一直没操作,今天保持卖出股票状态
|
||
* 状态三:今天卖出了股票
|
||
* 状态四:今天为冷冻期状态,但冷冻期状态不可持续,只有一天!
|
||
|
||
j的状态为:
|
||
|
||
* 0:状态一
|
||
* 1:状态二
|
||
* 2:状态三
|
||
* 3:状态四
|
||
|
||
很多题解为什么讲的比较模糊,是因为把这四个状态合并成三个状态了,其实就是把状态二和状态四合并在一起了。
|
||
|
||
从代码上来看确实可以合并,但从逻辑上分析合并之后就很难理解了,所以我下面的讲解是按照这四个状态来的,把每一个状态分析清楚。
|
||
|
||
**注意这里的每一个状态,例如状态一,是买入股票状态并不是说今天已经就买入股票,而是说保存买入股票的状态即:可能是前几天买入的,之后一直没操作,所以保持买入股票的状态**。
|
||
|
||
2. 确定递推公式
|
||
|
||
|
||
达到买入股票状态(状态一)即:dp[i][0],有两个具体操作:
|
||
|
||
* 操作一:前一天就是持有股票状态(状态一),dp[i][0] = dp[i - 1][0]
|
||
* 操作二:今天买入了,有两种情况
|
||
* 前一天是冷冻期(状态四),dp[i - 1][3] - prices[i]
|
||
* 前一天是保持卖出股票状态(状态二),dp[i - 1][1] - prices[i]
|
||
|
||
所以操作二取最大值,即:max(dp[i - 1][3], dp[i - 1][1]) - prices[i]
|
||
|
||
那么dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
|
||
|
||
达到保持卖出股票状态(状态二)即:dp[i][1],有两个具体操作:
|
||
|
||
* 操作一:前一天就是状态二
|
||
* 操作二:前一天是冷冻期(状态四)
|
||
|
||
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
|
||
|
||
达到今天就卖出股票状态(状态三),即:dp[i][2] ,只有一个操作:
|
||
|
||
* 操作一:昨天一定是买入股票状态(状态一),今天卖出
|
||
|
||
即:dp[i][2] = dp[i - 1][0] + prices[i];
|
||
|
||
达到冷冻期状态(状态四),即:dp[i][3],只有一个操作:
|
||
|
||
* 操作一:昨天卖出了股票(状态三)
|
||
|
||
p[i][3] = dp[i - 1][2];
|
||
|
||
综上分析,递推代码如下:
|
||
|
||
```CPP
|
||
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i];
|
||
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
|
||
dp[i][2] = dp[i - 1][0] + prices[i];
|
||
dp[i][3] = dp[i - 1][2];
|
||
```
|
||
|
||
3. dp数组如何初始化
|
||
|
||
这里主要讨论一下第0天如何初始化。
|
||
|
||
如果是持有股票状态(状态一)那么:dp[0][0] = -prices[0],买入股票所省现金为负数。
|
||
|
||
保持卖出股票状态(状态二),第0天没有卖出dp[0][1]初始化为0就行,
|
||
|
||
今天卖出了股票(状态三),同样dp[0][2]初始化为0,因为最少收益就是0,绝不会是负数。
|
||
|
||
同理dp[0][3]也初始为0。
|
||
|
||
|
||
4. 确定遍历顺序
|
||
|
||
从递归公式上可以看出,dp[i] 依赖于 dp[i-1],所以是从前向后遍历。
|
||
|
||
5. 举例推导dp数组
|
||
|
||
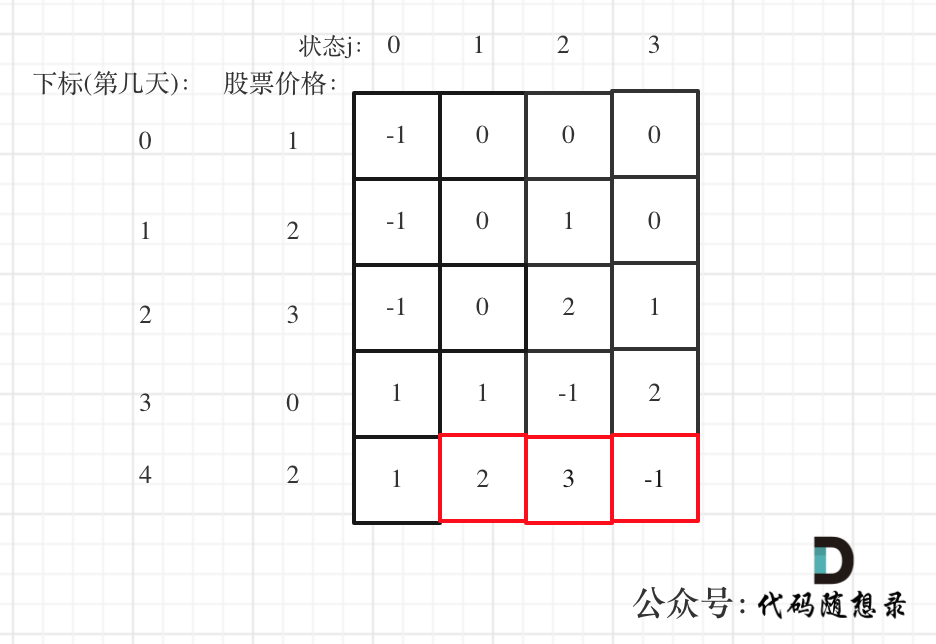
以 [1,2,3,0,2] 为例,dp数组如下:
|
||
|
||
|
||
|
||
最后结果去是 状态二,状态三,和状态四的最大值,不少同学会把状态四忘了,状态四是冷冻期,最后一天如果是冷冻期也可能是最大值。
|
||
|
||
代码如下:
|
||
|
||
```CPP
|
||
class Solution {
|
||
public:
|
||
int maxProfit(vector<int>& prices) {
|
||
int n = prices.size();
|
||
if (n == 0) return 0;
|
||
vector<vector<int>> dp(n, vector<int>(4, 0));
|
||
dp[0][0] -= prices[0]; // 持股票
|
||
for (int i = 1; i < n; i++) {
|
||
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][3], dp[i - 1][1]) - prices[i]);
|
||
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3]);
|
||
dp[i][2] = dp[i - 1][0] + prices[i];
|
||
dp[i][3] = dp[i - 1][2];
|
||
}
|
||
return max(dp[n - 1][3],max(dp[n - 1][1], dp[n - 1][2]));
|
||
}
|
||
};
|
||
```
|
||
|
||
* 时间复杂度:O(n)
|
||
* 空间复杂度:O(n)
|
||
|
||
当然,空间复杂度可以优化,定义一个dp[2][4]大小的数组就可以了,就保存前一天的当前的状态,感兴趣的同学可以自己去写一写,思路是一样的。
|
||
|
||
## 总结
|
||
|
||
这次把冷冻期这道题目,讲的很透彻了,细分为四个状态,其状态转移也十分清晰,建议大家都按照四个状态来分析,如果只划分三个状态确实很容易给自己绕进去。
|
||
|
||
## 其他语言版本
|
||
|
||
Java:
|
||
|
||
```java
|
||
class Solution {
|
||
public int maxProfit(int[] prices) {
|
||
if (prices == null || prices.length < 2) {
|
||
return 0;
|
||
}
|
||
int[][] dp = new int[prices.length][2];
|
||
|
||
// bad case
|
||
dp[0][0] = 0;
|
||
dp[0][1] = -prices[0];
|
||
dp[1][0] = Math.max(dp[0][0], dp[0][1] + prices[1]);
|
||
dp[1][1] = Math.max(dp[0][1], -prices[1]);
|
||
|
||
for (int i = 2; i < prices.length; i++) {
|
||
// dp公式
|
||
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
|
||
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 2][0] - prices[i]);
|
||
}
|
||
|
||
return dp[prices.length - 1][0];
|
||
}
|
||
}
|
||
```
|
||
|
||
```java
|
||
// 一维数组优化
|
||
class Solution {
|
||
public int maxProfit(int[] prices) {
|
||
// dp[2]和dp[3]用来存储冷冻期的数据
|
||
int[] dp=new int[4];
|
||
// 0表示持有,1表示卖出
|
||
dp[0] = -prices[0];
|
||
dp[1] = 0;
|
||
for(int i = 1; i <= prices.length; i++){
|
||
// 使用临时变量来保存dp[0], dp[2]
|
||
// 因为马上dp[0]和dp[2]的数据都会变
|
||
int temp = dp[0];
|
||
int temp1 = dp[2];
|
||
dp[0] = Math.max(dp[0], Math.max(dp[3], dp[1]) - prices[i-1]);
|
||
dp[1] = Math.max(dp[1], dp[3]);
|
||
dp[2] = temp + prices[i-1];
|
||
dp[3] = temp1;
|
||
}
|
||
return Math.max(dp[3],Math.max(dp[1],dp[2]));
|
||
}
|
||
}
|
||
```
|
||
|
||
Python:
|
||
|
||
```python
|
||
class Solution:
|
||
def maxProfit(self, prices: List[int]) -> int:
|
||
n = len(prices)
|
||
if n == 0:
|
||
return 0
|
||
dp = [[0] * 4 for _ in range(n)]
|
||
dp[0][0] = -prices[0] #持股票
|
||
for i in range(1, n):
|
||
dp[i][0] = max(dp[i-1][0], max(dp[i-1][3], dp[i-1][1]) - prices[i])
|
||
dp[i][1] = max(dp[i-1][1], dp[i-1][3])
|
||
dp[i][2] = dp[i-1][0] + prices[i]
|
||
dp[i][3] = dp[i-1][2]
|
||
return max(dp[n-1][3], dp[n-1][1], dp[n-1][2])
|
||
```
|
||
|
||
Go:
|
||
```go
|
||
// 最佳买卖股票时机含冷冻期 动态规划
|
||
// 时间复杂度O(n) 空间复杂度O(n)
|
||
func maxProfit(prices []int) int {
|
||
n := len(prices)
|
||
if n < 2 {
|
||
return 0
|
||
}
|
||
|
||
dp := make([][]int, n)
|
||
status := make([]int, n * 4)
|
||
for i := range dp {
|
||
dp[i] = status[:4]
|
||
status = status[4:]
|
||
}
|
||
dp[0][0] = -prices[0]
|
||
|
||
for i := 1; i < n; i++ {
|
||
dp[i][0] = max(dp[i - 1][0], max(dp[i - 1][1] - prices[i], dp[i - 1][3] - prices[i]))
|
||
dp[i][1] = max(dp[i - 1][1], dp[i - 1][3])
|
||
dp[i][2] = dp[i - 1][0] + prices[i]
|
||
dp[i][3] = dp[i - 1][2]
|
||
}
|
||
|
||
return max(dp[n - 1][1], max(dp[n - 1][2], dp[n - 1][3]))
|
||
}
|
||
|
||
func max(a, b int) int {
|
||
if a > b {
|
||
return a
|
||
}
|
||
return b
|
||
}
|
||
```
|
||
|
||
Javascript:
|
||
|
||
```javascript
|
||
const maxProfit = (prices) => {
|
||
if(prices.length < 2) {
|
||
return 0
|
||
} else if(prices.length < 3) {
|
||
return Math.max(0, prices[1] - prices[0]);
|
||
}
|
||
|
||
let dp = Array.from(Array(prices.length), () => Array(4).fill(0));
|
||
dp[0][0] = 0 - prices[0];
|
||
|
||
for(i = 1; i < prices.length; i++) {
|
||
dp[i][0] = Math.max(dp[i - 1][0], Math.max(dp[i-1][1], dp[i-1][3]) - prices[i]);
|
||
dp[i][1] = Math.max(dp[i -1][1], dp[i - 1][3]);
|
||
dp[i][2] = dp[i-1][0] + prices[i];
|
||
dp[i][3] = dp[i-1][2];
|
||
}
|
||
|
||
return Math.max(dp[prices.length - 1][1], dp[prices.length - 1][2], dp[prices.length - 1][3]);
|
||
};
|
||
```
|
||
|
||
|
||
-----------------------
|
||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码一.jpg width=500> </img></div>
|