mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2026-02-02 18:39:09 +08:00
144 lines
6.3 KiB
Markdown
144 lines
6.3 KiB
Markdown
|
||
# 通过一道面试题目,讲一讲递归算法的时间复杂度!
|
||
|
||
> 本篇通过一道面试题,一个面试场景,来好好分析一下如何求递归算法的时间复杂度。
|
||
|
||
相信很多同学对递归算法的时间复杂度都很模糊,那么这篇来给大家通透的讲一讲。
|
||
|
||
**同一道题目,同样使用递归算法,有的同学会写出了O(n)的代码,有的同学就写出了O(logn)的代码**。
|
||
|
||
这是为什么呢?
|
||
|
||
如果对递归的时间复杂度理解的不够深入的话,就会这样!
|
||
|
||
那么我通过一道简单的面试题,模拟面试的场景,来带大家逐步分析递归算法的时间复杂度,最后找出最优解,来看看同样是递归,怎么就写成了O(n)的代码。
|
||
|
||
面试题:求x的n次方
|
||
|
||
想一下这么简单的一道题目,代码应该如何写呢。最直观的方式应该就是,一个for循环求出结果,代码如下:
|
||
|
||
```CPP
|
||
int function1(int x, int n) {
|
||
int result = 1; // 注意 任何数的0次方等于1
|
||
for (int i = 0; i < n; i++) {
|
||
result = result * x;
|
||
}
|
||
return result;
|
||
}
|
||
```
|
||
时间复杂度为O(n),此时面试官会说,有没有效率更好的算法呢。
|
||
|
||
**如果此时没有思路,不要说:我不会,我不知道了等等**。
|
||
|
||
可以和面试官探讨一下,询问:“可不可以给点提示”。面试官提示:“考虑一下递归算法”。
|
||
|
||
那么就可以写出了如下这样的一个递归的算法,使用递归解决了这个问题。
|
||
|
||
```CPP
|
||
int function2(int x, int n) {
|
||
if (n == 0) {
|
||
return 1; // return 1 同样是因为0次方是等于1的
|
||
}
|
||
return function2(x, n - 1) * x;
|
||
}
|
||
```
|
||
面试官问:“那么这个代码的时间复杂度是多少?”。
|
||
|
||
一些同学可能一看到递归就想到了O(log n),其实并不是这样,递归算法的时间复杂度本质上是要看: **递归的次数 * 每次递归中的操作次数**。
|
||
|
||
那再来看代码,这里递归了几次呢?
|
||
|
||
每次n-1,递归了n次时间复杂度是O(n),每次进行了一个乘法操作,乘法操作的时间复杂度一个常数项O(1),所以这份代码的时间复杂度是 n × 1 = O(n)。
|
||
|
||
这个时间复杂度就没有达到面试官的预期。于是又写出了如下的递归算法的代码:
|
||
|
||
```CPP
|
||
int function3(int x, int n) {
|
||
if (n == 0) return 1;
|
||
if (n == 1) return x;
|
||
|
||
if (n % 2 == 1) {
|
||
return function3(x, n / 2) * function3(x, n / 2)*x;
|
||
}
|
||
return function3(x, n / 2) * function3(x, n / 2);
|
||
}
|
||
|
||
```
|
||
|
||
面试官看到后微微一笑,问:“这份代码的时间复杂度又是多少呢?” 此刻有些同学可能要陷入了沉思了。
|
||
|
||
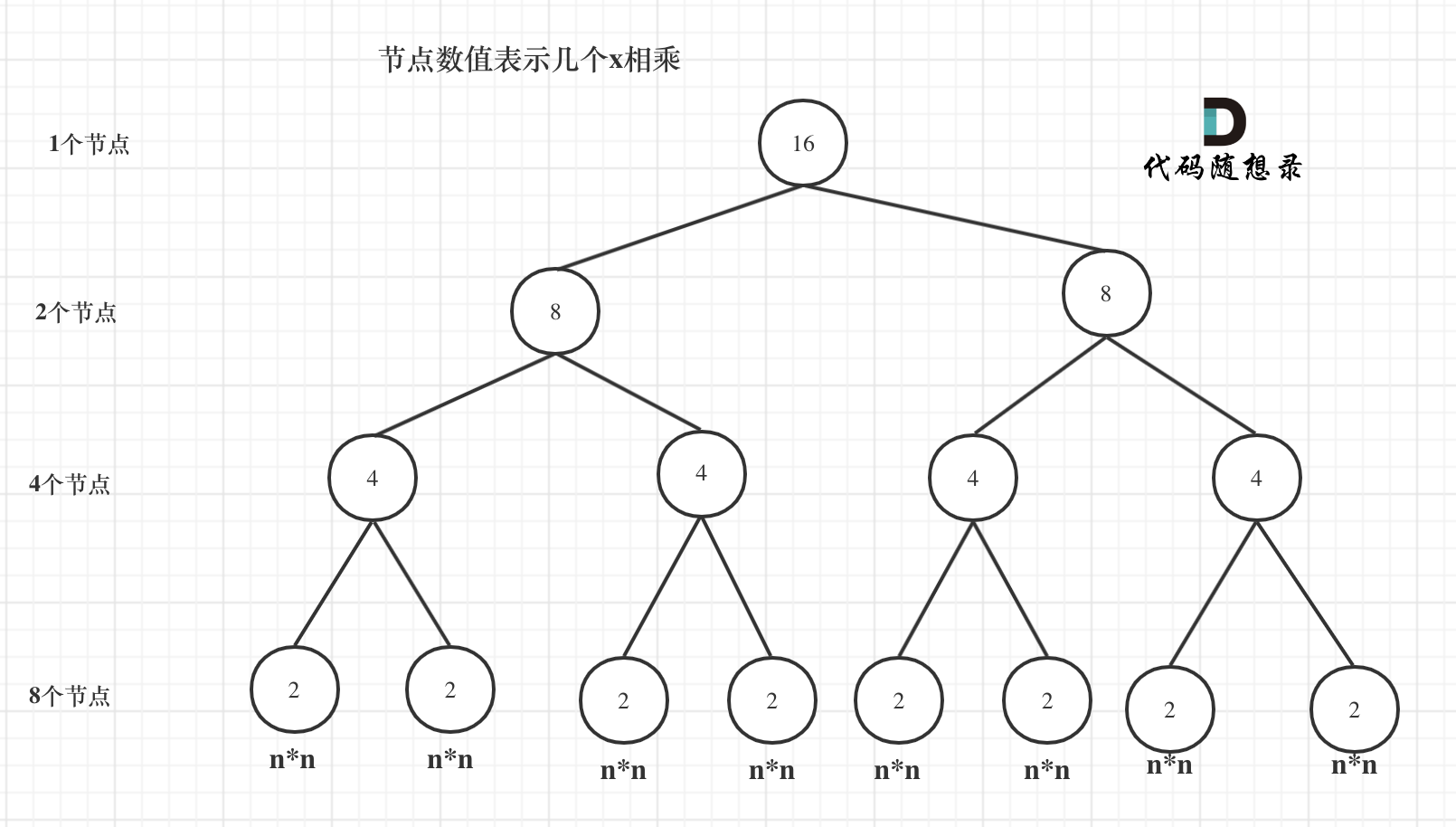
我们来分析一下,首先看递归了多少次呢,可以把递归抽象出一棵满二叉树。刚刚同学写的这个算法,可以用一棵满二叉树来表示(为了方便表示,选择n为偶数16),如图:
|
||
|
||
|
||
|
||
当前这棵二叉树就是求x的n次方,n为16的情况,n为16的时候,进行了多少次乘法运算呢?
|
||
|
||
这棵树上每一个节点就代表着一次递归并进行了一次相乘操作,所以进行了多少次递归的话,就是看这棵树上有多少个节点。
|
||
|
||
熟悉二叉树话应该知道如何求满二叉树节点数量,这棵满二叉树的节点数量就是`2^3 + 2^2 + 2^1 + 2^0 = 15`,可以发现:**这其实是等比数列的求和公式,这个结论在二叉树相关的面试题里也经常出现**。
|
||
|
||
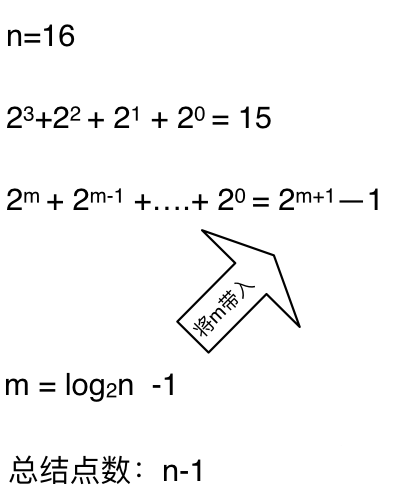
这么如果是求x的n次方,这个递归树有多少个节点呢,如下图所示:(m为深度,从0开始)
|
||
|
||
|
||
|
||
**时间复杂度忽略掉常数项`-1`之后,这个递归算法的时间复杂度依然是O(n)**。对,你没看错,依然是O(n)的时间复杂度!
|
||
|
||
此时面试官就会说:“这个递归的算法依然还是O(n)啊”, 很明显没有达到面试官的预期。
|
||
|
||
那么O(logn)的递归算法应该怎么写呢?
|
||
|
||
想一想刚刚给出的那份递归算法的代码,是不是有哪里比较冗余呢,其实有重复计算的部分。
|
||
|
||
于是又写出如下递归算法的代码:
|
||
|
||
```CPP
|
||
int function4(int x, int n) {
|
||
if (n == 0) return 1;
|
||
if (n == 1) return x;
|
||
int t = function4(x, n / 2);// 这里相对于function3,是把这个递归操作抽取出来
|
||
if (n % 2 == 1) {
|
||
return t * t * x;
|
||
}
|
||
return t * t;
|
||
}
|
||
```
|
||
|
||
再来看一下现在这份代码时间复杂度是多少呢?
|
||
|
||
依然还是看他递归了多少次,可以看到这里仅仅有一个递归调用,且每次都是n/2 ,所以这里我们一共调用了log以2为底n的对数次。
|
||
|
||
**每次递归了做都是一次乘法操作,这也是一个常数项的操作,那么这个递归算法的时间复杂度才是真正的O(logn)**。
|
||
|
||
此时大家最后写出了这样的代码并且将时间复杂度分析的非常清晰,相信面试官是比较满意的。
|
||
|
||
# 总结
|
||
|
||
对于递归的时间复杂度,毕竟初学者有时候会迷糊,刷过很多题的老手依然迷糊。
|
||
|
||
**本篇我用一道非常简单的面试题目:求x的n次方,来逐步分析递归算法的时间复杂度,注意不要一看到递归就想到了O(logn)!**
|
||
|
||
同样使用递归,有的同学可以写出O(logn)的代码,有的同学还可以写出O(n)的代码。
|
||
|
||
对于function3 这样的递归实现,很容易让人感觉这是O(log n)的时间复杂度,其实这是O(n)的算法!
|
||
|
||
```CPP
|
||
int function3(int x, int n) {
|
||
if (n == 0) return 1;
|
||
if (n == 1) return x;
|
||
if (n % 2 == 1) {
|
||
return function3(x, n / 2) * function3(x, n / 2)*x;
|
||
}
|
||
return function3(x, n / 2) * function3(x, n / 2);
|
||
}
|
||
```
|
||
可以看出这道题目非常简单,但是又很考究算法的功底,特别是对递归的理解,这也是我面试别人的时候用过的一道题,所以整个情景我才写的如此逼真。
|
||
|
||
大厂面试的时候最喜欢用“简单题”来考察候选人的算法功底,注意这里的“简单题”可并不一定真的简单哦!
|
||
|
||
如果认真读完本篇,相信大家对递归算法的有一个新的认识的,同一道题目,同样是递归,效率可是不一样的!
|
||
|
||
|
||
|
||
-----------------------
|
||
<div align="center"><img src='https://file1.kamacoder.com/i/algo/01二维码.jpg' width=450> </img></div>
|