mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2026-02-02 18:39:09 +08:00
643 lines
19 KiB
Markdown
Executable File
643 lines
19 KiB
Markdown
Executable File
* [做项目(多个C++、Java、Go、测开、前端项目)](https://www.programmercarl.com/other/kstar.html)
|
||
* [刷算法(两个月高强度学算法)](https://www.programmercarl.com/xunlian/xunlianying.html)
|
||
* [背八股(40天挑战高频面试题)](https://www.programmercarl.com/xunlian/bagu.html)
|
||
|
||
# 188.买卖股票的最佳时机IV
|
||
|
||
[力扣题目链接](https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/)
|
||
|
||
给定一个整数数组 prices ,它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。
|
||
|
||
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。
|
||
|
||
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
|
||
|
||
* 示例 1:
|
||
* 输入:k = 2, prices = [2,4,1]
|
||
* 输出:2
|
||
解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2。
|
||
|
||
* 示例 2:
|
||
* 输入:k = 2, prices = [3,2,6,5,0,3]
|
||
* 输出:7
|
||
解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
|
||
|
||
|
||
提示:
|
||
|
||
* 0 <= k <= 100
|
||
* 0 <= prices.length <= 1000
|
||
* 0 <= prices[i] <= 1000
|
||
|
||
## 算法公开课
|
||
|
||
**[《代码随想录》算法视频公开课](https://programmercarl.com/other/gongkaike.html):[动态规划来决定最佳时机,至多可以买卖K次!| LeetCode:188.买卖股票最佳时机4](https://www.bilibili.com/video/BV16M411U7XJ),相信结合视频再看本篇题解,更有助于大家对本题的理解**。
|
||
|
||
|
||
## 思路
|
||
|
||
这道题目可以说是[动态规划:123.买卖股票的最佳时机III](https://programmercarl.com/0123.买卖股票的最佳时机III.html)的进阶版,这里要求至多有k次交易。
|
||
|
||
动规五部曲,分析如下:
|
||
|
||
1. 确定dp数组以及下标的含义
|
||
|
||
在[动态规划:123.买卖股票的最佳时机III](https://programmercarl.com/0123.买卖股票的最佳时机III.html)中,我是定义了一个二维dp数组,本题其实依然可以用一个二维dp数组。
|
||
|
||
使用二维数组 dp[i][j] :第i天的状态为j,所剩下的最大现金是dp[i][j]
|
||
|
||
j的状态表示为:
|
||
|
||
* 0 表示不操作
|
||
* 1 第一次买入
|
||
* 2 第一次卖出
|
||
* 3 第二次买入
|
||
* 4 第二次卖出
|
||
* .....
|
||
|
||
**大家应该发现规律了吧 ,除了0以外,偶数就是卖出,奇数就是买入**。
|
||
|
||
题目要求是至多有K笔交易,那么j的范围就定义为 2 * k + 1 就可以了。
|
||
|
||
所以二维dp数组的C++定义为:
|
||
|
||
```CPP
|
||
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
|
||
```
|
||
|
||
2. 确定递推公式
|
||
|
||
还要强调一下:dp[i][1],**表示的是第i天,买入股票的状态,并不是说一定要第i天买入股票,这是很多同学容易陷入的误区**。
|
||
|
||
达到dp[i][1]状态,有两个具体操作:
|
||
|
||
* 操作一:第i天买入股票了,那么dp[i][1] = dp[i - 1][0] - prices[i]
|
||
* 操作二:第i天没有操作,而是沿用前一天买入的状态,即:dp[i][1] = dp[i - 1][1]
|
||
|
||
选最大的,所以 dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1]);
|
||
|
||
同理dp[i][2]也有两个操作:
|
||
|
||
* 操作一:第i天卖出股票了,那么dp[i][2] = dp[i - 1][1] + prices[i]
|
||
* 操作二:第i天没有操作,沿用前一天卖出股票的状态,即:dp[i][2] = dp[i - 1][2]
|
||
|
||
所以dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
|
||
|
||
同理可以类比剩下的状态,代码如下:
|
||
|
||
```CPP
|
||
for (int j = 0; j < 2 * k - 1; j += 2) {
|
||
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
|
||
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
|
||
}
|
||
```
|
||
|
||
**本题和[动态规划:123.买卖股票的最佳时机III](https://programmercarl.com/0123.买卖股票的最佳时机III.html)最大的区别就是这里要类比j为奇数是买,偶数是卖的状态**。
|
||
|
||
3. dp数组如何初始化
|
||
|
||
第0天没有操作,这个最容易想到,就是0,即:dp[0][0] = 0;
|
||
|
||
第0天做第一次买入的操作,dp[0][1] = -prices[0];
|
||
|
||
第0天做第一次卖出的操作,这个初始值应该是多少呢?
|
||
|
||
此时还没有买入,怎么就卖出呢? 其实大家可以理解当天买入,当天卖出,所以dp[0][2] = 0;
|
||
|
||
第0天第二次买入操作,初始值应该是多少呢?应该不少同学疑惑,第一次还没买入呢,怎么初始化第二次买入呢?
|
||
|
||
第二次买入依赖于第一次卖出的状态,其实相当于第0天第一次买入了,第一次卖出了,然后在买入一次(第二次买入),那么现在手头上没有现金,只要买入,现金就做相应的减少。
|
||
|
||
所以第二次买入操作,初始化为:dp[0][3] = -prices[0];
|
||
|
||
第二次卖出初始化dp[0][4] = 0;
|
||
|
||
**所以同理可以推出dp[0][j]当j为奇数的时候都初始化为 -prices[0]**
|
||
|
||
代码如下:
|
||
|
||
```CPP
|
||
for (int j = 1; j < 2 * k; j += 2) {
|
||
dp[0][j] = -prices[0];
|
||
}
|
||
```
|
||
|
||
**在初始化的地方同样要类比j为偶数是卖、奇数是买的状态**。
|
||
|
||
4. 确定遍历顺序
|
||
|
||
从递归公式其实已经可以看出,一定是从前向后遍历,因为dp[i],依靠dp[i - 1]的数值。
|
||
|
||
5. 举例推导dp数组
|
||
|
||
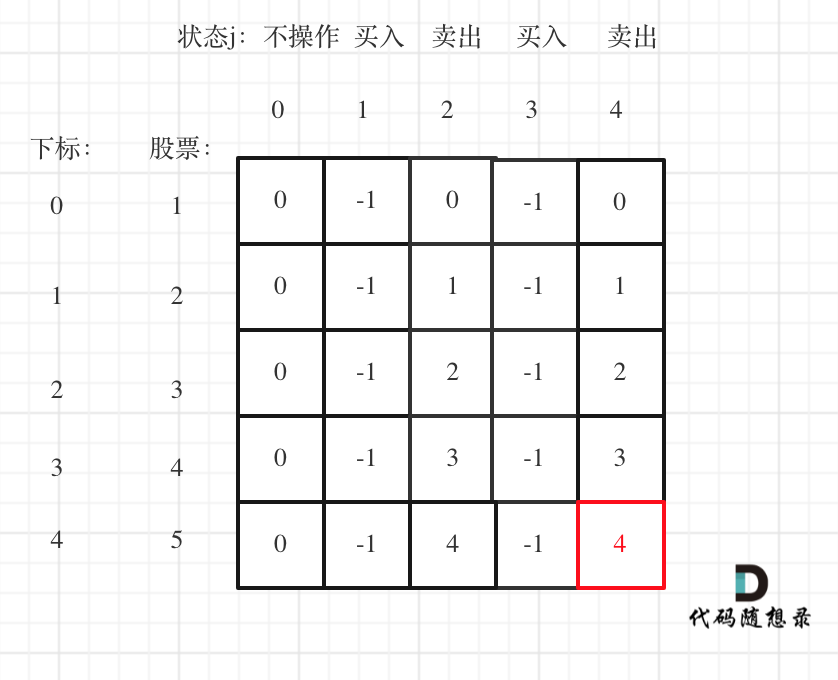
以输入[1,2,3,4,5],k=2为例。
|
||
|
||
|
||
|
||
最后一次卖出,一定是利润最大的,dp[prices.size() - 1][2 * k]即红色部分就是最后求解。
|
||
|
||
以上分析完毕,C++代码如下:
|
||
|
||
```CPP
|
||
class Solution {
|
||
public:
|
||
int maxProfit(int k, vector<int>& prices) {
|
||
|
||
if (prices.size() == 0) return 0;
|
||
vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));
|
||
for (int j = 1; j < 2 * k; j += 2) {
|
||
dp[0][j] = -prices[0];
|
||
}
|
||
for (int i = 1;i < prices.size(); i++) {
|
||
for (int j = 0; j < 2 * k - 1; j += 2) {
|
||
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
|
||
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
|
||
}
|
||
}
|
||
return dp[prices.size() - 1][2 * k];
|
||
}
|
||
};
|
||
```
|
||
|
||
* 时间复杂度: O(n * k),其中 n 为 prices 的长度
|
||
* 空间复杂度: O(n * k)
|
||
|
||
|
||
|
||
当然有的解法是定义一个三维数组dp[i][j][k],第i天,第j次买卖,k表示买还是卖的状态,从定义上来讲是比较直观。
|
||
|
||
但感觉三维数组操作起来有些麻烦,我是直接用二维数组来模拟三维数组的情况,代码看起来也清爽一些。
|
||
|
||
|
||
## 其他语言版本
|
||
|
||
### Java:
|
||
|
||
```java
|
||
// 版本一: 三维 dp数组
|
||
class Solution {
|
||
public int maxProfit(int k, int[] prices) {
|
||
if (prices.length == 0) return 0;
|
||
|
||
// [天数][交易次数][是否持有股票]
|
||
int len = prices.length;
|
||
int[][][] dp = new int[len][k + 1][2];
|
||
|
||
// dp数组初始化
|
||
// 初始化所有的交易次数是为确保 最后结果是最多 k 次买卖的最大利润
|
||
for (int i = 0; i <= k; i++) {
|
||
dp[0][i][1] = -prices[0];
|
||
}
|
||
|
||
for (int i = 1; i < len; i++) {
|
||
for (int j = 1; j <= k; j++) {
|
||
// dp方程, 0表示不持有/卖出, 1表示持有/买入
|
||
dp[i][j][0] = Math.max(dp[i - 1][j][0], dp[i - 1][j][1] + prices[i]);
|
||
dp[i][j][1] = Math.max(dp[i - 1][j][1], dp[i - 1][j - 1][0] - prices[i]);
|
||
}
|
||
}
|
||
return dp[len - 1][k][0];
|
||
}
|
||
}
|
||
|
||
// 版本二: 二维 dp数组
|
||
class Solution {
|
||
public int maxProfit(int k, int[] prices) {
|
||
if (prices.length == 0) return 0;
|
||
|
||
// [天数][股票状态]
|
||
// 股票状态: 奇数表示第 k 次交易持有/买入, 偶数表示第 k 次交易不持有/卖出, 0 表示没有操作
|
||
int len = prices.length;
|
||
int[][] dp = new int[len][k*2 + 1];
|
||
|
||
// dp数组的初始化, 与版本一同理
|
||
for (int i = 1; i < k*2; i += 2) {
|
||
dp[0][i] = -prices[0];
|
||
}
|
||
|
||
for (int i = 1; i < len; i++) {
|
||
for (int j = 0; j < k*2 - 1; j += 2) {
|
||
dp[i][j + 1] = Math.max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
|
||
dp[i][j + 2] = Math.max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
|
||
}
|
||
}
|
||
return dp[len - 1][k*2];
|
||
}
|
||
}
|
||
|
||
//版本三:一维 dp数组 (下面有和卡哥邏輯一致的一維數組JAVA解法)
|
||
class Solution {
|
||
public int maxProfit(int k, int[] prices) {
|
||
if(prices.length == 0){
|
||
return 0;
|
||
}
|
||
if(k == 0){
|
||
return 0;
|
||
}
|
||
// 其实就是123题的扩展,123题只用记录2次交易的状态
|
||
// 这里记录k次交易的状态就行了
|
||
// 每次交易都有买入,卖出两个状态,所以要乘 2
|
||
int[] dp = new int[2 * k];
|
||
// 按123题解题格式那样,做一个初始化
|
||
for(int i = 0; i < dp.length / 2; i++){
|
||
dp[i * 2] = -prices[0];
|
||
}
|
||
for(int i = 1; i <= prices.length; i++){
|
||
dp[0] = Math.max(dp[0], -prices[i - 1]);
|
||
dp[1] = Math.max(dp[1], dp[0] + prices[i - 1]);
|
||
// 还是与123题一样,与123题对照来看
|
||
// 就很容易啦
|
||
for(int j = 2; j < dp.length; j += 2){
|
||
dp[j] = Math.max(dp[j], dp[j - 1] - prices[i-1]);
|
||
dp[j + 1] = Math.max(dp[j + 1], dp[j] + prices[i - 1]);
|
||
}
|
||
}
|
||
// 返回最后一次交易卖出状态的结果就行了
|
||
return dp[dp.length - 1];
|
||
}
|
||
}
|
||
```
|
||
```JAVA
|
||
class Solution {
|
||
public int maxProfit(int k, int[] prices) {
|
||
|
||
//edge cases
|
||
if(prices.length == 0 || k == 0)
|
||
return 0;
|
||
|
||
|
||
int dp[] = new int [k * 2 + 1];
|
||
|
||
//和卡哥邏輯一致,奇數天購入股票,故初始化只初始化奇數天。
|
||
for(int i = 1; i < 2 * k + 1; i += 2){
|
||
dp[i] = -prices[0];
|
||
}
|
||
|
||
for(int i = 1; i < prices.length; i++){ //i 從 1 開始,因爲第 i = 0 天已經透過初始化完成了。
|
||
for(int j = 1; j < 2 * k + 1; j++){ //j 從 1 開始,因爲第 j = 0 天已經透過初始化完成了。
|
||
//奇數天購買
|
||
if(j % 2 == 1)
|
||
dp[j] = Math.max(dp[j], dp[j - 1] - prices[i]);
|
||
//偶數天賣出
|
||
else
|
||
dp[j] = Math.max(dp[j], dp[j - 1] + prices[i]);
|
||
}
|
||
//打印DP數組
|
||
//for(int x : dp)
|
||
// System.out.print(x +", ");
|
||
//System.out.println();
|
||
}
|
||
//return 第2 * k次賣出的獲利。
|
||
return dp[2 * k];
|
||
}
|
||
}
|
||
```
|
||
|
||
### Python:
|
||
|
||
> 版本一
|
||
```python
|
||
class Solution:
|
||
def maxProfit(self, k: int, prices: List[int]) -> int:
|
||
if len(prices) == 0:
|
||
return 0
|
||
dp = [[0] * (2*k+1) for _ in range(len(prices))]
|
||
for j in range(1, 2*k, 2):
|
||
dp[0][j] = -prices[0]
|
||
for i in range(1, len(prices)):
|
||
for j in range(0, 2*k-1, 2):
|
||
dp[i][j+1] = max(dp[i-1][j+1], dp[i-1][j] - prices[i])
|
||
dp[i][j+2] = max(dp[i-1][j+2], dp[i-1][j+1] + prices[i])
|
||
return dp[-1][2*k]
|
||
```
|
||
|
||
> 版本二
|
||
```python
|
||
class Solution:
|
||
def maxProfit(self, k: int, prices: List[int]) -> int:
|
||
if len(prices) == 0: return 0
|
||
dp = [0] * (2*k + 1)
|
||
for i in range(1,2*k,2):
|
||
dp[i] = -prices[0]
|
||
for i in range(1,len(prices)):
|
||
for j in range(1,2*k + 1):
|
||
if j % 2:
|
||
dp[j] = max(dp[j],dp[j-1]-prices[i])
|
||
else:
|
||
dp[j] = max(dp[j],dp[j-1]+prices[i])
|
||
return dp[2*k]
|
||
```
|
||
|
||
> 版本三: 一维 dp 数组(易理解版本)
|
||
```python
|
||
class Solution:
|
||
def maxProfit(self, k: int, prices: List[int]) -> int:
|
||
dp = [0] * k * 2
|
||
for i in range(k):
|
||
dp[i * 2] = -prices[0]
|
||
|
||
for price in prices[1:]:
|
||
dc = dp.copy() # 这句话是关键,把前一天的 dp 状态保存下来,防止被覆盖掉,后面只用它,不用 dp,逻辑简单易懂
|
||
|
||
for i in range(2 * k):
|
||
if i % 2 == 1:
|
||
dp[i] = max(dc[i], dc[i - 1] + price)
|
||
else:
|
||
pre = 0 if i == 0 else dc[i - 1]
|
||
dp[i] = max(dc[i], pre - price)
|
||
|
||
return dp[-1]
|
||
```
|
||
|
||
### Go:
|
||
|
||
> 版本一:
|
||
|
||
```go
|
||
// 买卖股票的最佳时机IV 动态规划
|
||
// 时间复杂度O(kn) 空间复杂度O(kn)
|
||
func maxProfit(k int, prices []int) int {
|
||
if k == 0 || len(prices) == 0 {
|
||
return 0
|
||
}
|
||
|
||
dp := make([][]int, len(prices))
|
||
status := make([]int, (2 * k + 1) * len(prices))
|
||
for i := range dp {
|
||
dp[i] = status[:2 * k + 1]
|
||
status = status[2 * k + 1:]
|
||
}
|
||
for j := 1; j < 2 * k; j += 2 {
|
||
dp[0][j] = -prices[0]
|
||
}
|
||
|
||
for i := 1; i < len(prices); i++ {
|
||
for j := 0; j < 2 * k; j += 2 {
|
||
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i])
|
||
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i])
|
||
}
|
||
}
|
||
return dp[len(prices) - 1][2 * k]
|
||
}
|
||
|
||
func max(a, b int) int {
|
||
if a > b {
|
||
return a
|
||
}
|
||
return b
|
||
}
|
||
```
|
||
|
||
> 版本二: 三维 dp数组
|
||
```go
|
||
func maxProfit(k int, prices []int) int {
|
||
length := len(prices)
|
||
if length == 0 {
|
||
return 0
|
||
}
|
||
// [天数][交易次数][是否持有股票]
|
||
// 1表示不持有/卖出, 0表示持有/买入
|
||
dp := make([][][]int, length)
|
||
for i := 0; i < length; i++ {
|
||
dp[i] = make([][]int, k+1)
|
||
for j := 0; j <= k; j++ {
|
||
dp[i][j] = make([]int, 2)
|
||
}
|
||
}
|
||
for j := 0; j <= k; j++ {
|
||
dp[0][j][0] = -prices[0]
|
||
}
|
||
for i := 1; i < length; i++ {
|
||
for j := 1; j <= k; j++ {
|
||
dp[i][j][0] = max188(dp[i-1][j][0], dp[i-1][j-1][1]-prices[i])
|
||
dp[i][j][1] = max188(dp[i-1][j][1], dp[i-1][j][0]+prices[i])
|
||
}
|
||
}
|
||
return dp[length-1][k][1]
|
||
}
|
||
|
||
func max188(a, b int) int {
|
||
if a > b {
|
||
return a
|
||
}
|
||
return b
|
||
}
|
||
```
|
||
|
||
版本三:空间优化版本
|
||
|
||
```go
|
||
func maxProfit(k int, prices []int) int {
|
||
n := len(prices)
|
||
// k次交易,2 * k种状态
|
||
// 状态从1开始计算,避免判断
|
||
// 奇数时持有(保持或买入)
|
||
// 偶数时不持有(保持或卖出)
|
||
dp := make([][]int, 2)
|
||
dp[0] = make([]int, k * 2 + 1)
|
||
dp[1] = make([]int, k * 2 + 1)
|
||
|
||
// 奇数状态时持有,i += 2
|
||
for i := 1; i <= k * 2; i += 2 {
|
||
dp[0][i] = -prices[0]
|
||
}
|
||
|
||
for i := 1; i < len(prices); i++ {
|
||
for j := 1; j <= k * 2; j++ {
|
||
if j % 2 == 1 {
|
||
dp[i % 2][j] = max(dp[(i - 1) % 2][j], dp[(i - 1) % 2][j - 1] - prices[i])
|
||
} else {
|
||
dp[i % 2][j] = max(dp[(i - 1) % 2][j], dp[(i - 1) % 2][j - 1] + prices[i])
|
||
}
|
||
}
|
||
}
|
||
|
||
return dp[(n - 1) % 2][k * 2]
|
||
}
|
||
|
||
func max(a, b int) int {
|
||
if a > b {
|
||
return a
|
||
}
|
||
return b
|
||
}
|
||
```
|
||
|
||
> 版本四:一维 dp 数组(易理解版本)
|
||
|
||
```go
|
||
func maxProfit(k int, prices []int) int {
|
||
dp := make([]int, 2 * k)
|
||
for i := range k {
|
||
dp[i * 2] = -prices[0]
|
||
}
|
||
|
||
for j := 1; j < len(prices); j++ {
|
||
dc := slices.Clone(dp) // 这句话是关键,把前一天的 dp 状态保存下来,防止被覆盖掉,后面只用它,不用 dp,逻辑简单易懂
|
||
|
||
for i := range k * 2 {
|
||
if i % 2 == 1 {
|
||
dp[i] = max(dc[i], dc[i - 1] + prices[j])
|
||
} else {
|
||
pre := 0; if i >= 1 { pre = dc[i - 1] }
|
||
dp[i] = max(dc[i], pre - prices[j])
|
||
}
|
||
}
|
||
}
|
||
|
||
return dp[2 * k - 1]
|
||
}
|
||
```
|
||
|
||
### JavaScript:
|
||
|
||
```javascript
|
||
// 方法一:动态规划
|
||
const maxProfit = (k,prices) => {
|
||
if (prices == null || prices.length < 2 || k == 0) {
|
||
return 0;
|
||
}
|
||
|
||
let dp = Array.from(Array(prices.length), () => Array(2*k+1).fill(0));
|
||
|
||
for (let j = 1; j < 2 * k; j += 2) {
|
||
dp[0][j] = 0 - prices[0];
|
||
}
|
||
|
||
for(let i = 1; i < prices.length; i++) {
|
||
for (let j = 0; j < 2 * k; j += 2) {
|
||
dp[i][j+1] = Math.max(dp[i-1][j+1], dp[i-1][j] - prices[i]);
|
||
dp[i][j+2] = Math.max(dp[i-1][j+2], dp[i-1][j+1] + prices[i]);
|
||
}
|
||
}
|
||
|
||
return dp[prices.length - 1][2 * k];
|
||
};
|
||
|
||
// 方法二:动态规划+空间优化
|
||
var maxProfit = function(k, prices) {
|
||
let n = prices.length;
|
||
let dp = new Array(2*k+1).fill(0);
|
||
// dp 买入状态初始化
|
||
for (let i = 1; i <= 2*k; i += 2) {
|
||
dp[i] = - prices[0];
|
||
}
|
||
|
||
for (let i = 1; i < n; i++) {
|
||
for (let j = 1; j < 2*k+1; j++) {
|
||
// j 为奇数:买入状态
|
||
if (j % 2) {
|
||
dp[j] = Math.max(dp[j], dp[j-1] - prices[i]);
|
||
} else {
|
||
// j为偶数:卖出状态
|
||
dp[j] = Math.max(dp[j], dp[j-1] + prices[i]);
|
||
}
|
||
}
|
||
}
|
||
|
||
return dp[2*k];
|
||
};
|
||
```
|
||
|
||
### TypeScript:
|
||
|
||
```typescript
|
||
function maxProfit(k: number, prices: number[]): number {
|
||
const length: number = prices.length;
|
||
if (length === 0) return 0;
|
||
const dp: number[][] = new Array(length).fill(0)
|
||
.map(_ => new Array(k * 2 + 1).fill(0));
|
||
for (let i = 1; i <= k; i++) {
|
||
dp[0][i * 2 - 1] = -prices[0];
|
||
}
|
||
for (let i = 1; i < length; i++) {
|
||
for (let j = 1; j < 2 * k + 1; j++) {
|
||
dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - 1] + Math.pow(-1, j) * prices[i]);
|
||
}
|
||
}
|
||
return dp[length - 1][2 * k];
|
||
};
|
||
```
|
||
|
||
### C:
|
||
|
||
```c
|
||
#define max(a, b) ((a) > (b) ? (a) : (b))
|
||
|
||
int maxProfit(int k, int* prices, int pricesSize) {
|
||
if(pricesSize == 0){
|
||
return 0;
|
||
}
|
||
|
||
int dp[pricesSize][2 * k + 1];
|
||
memset(dp, 0, sizeof(int) * pricesSize * (2 * k + 1));
|
||
for (int j = 1; j < 2 * k; j += 2) {
|
||
dp[0][j] = -prices[0];
|
||
}
|
||
|
||
for (int i = 1;i < pricesSize; i++) {//枚举股票
|
||
for (int j = 0; j < 2 * k - 1; j += 2) { //更新每一次买入卖出
|
||
dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);
|
||
dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);
|
||
}
|
||
}
|
||
return dp[pricesSize - 1][2 * k];
|
||
}
|
||
```
|
||
|
||
|
||
|
||
### Rust:
|
||
|
||
```rust
|
||
impl Solution {
|
||
pub fn max_profit(k: i32, prices: Vec<i32>) -> i32 {
|
||
let mut dp = vec![vec![0; 2 * k as usize + 1]; prices.len()];
|
||
|
||
for v in dp[0].iter_mut().skip(1).step_by(2) {
|
||
*v = -prices[0];
|
||
}
|
||
|
||
for (i, &p) in prices.iter().enumerate().skip(1) {
|
||
for j in (0..2 * k as usize - 1).step_by(2) {
|
||
dp[i][j + 1] = dp[i - 1][j + 1].max(dp[i - 1][j] - p);
|
||
dp[i][j + 2] = dp[i - 1][j + 2].max(dp[i - 1][j + 1] + p);
|
||
}
|
||
}
|
||
|
||
dp[prices.len() - 1][2 * k as usize]
|
||
}
|
||
}
|
||
```
|
||
|
||
空间优化:
|
||
|
||
```rust
|
||
impl Solution {
|
||
pub fn max_profit(k: i32, prices: Vec<i32>) -> i32 {
|
||
let mut dp = vec![0; 2 * k as usize + 1];
|
||
for v in dp.iter_mut().skip(1).step_by(2) {
|
||
*v = -prices[0];
|
||
}
|
||
|
||
for p in prices {
|
||
for i in 1..=2 * k as usize {
|
||
if i % 2 == 1 {
|
||
// 买入
|
||
dp[i] = dp[i].max(dp[i - 1] - p);
|
||
continue;
|
||
}
|
||
// 卖出
|
||
dp[i] = dp[i].max(dp[i - 1] + p);
|
||
}
|
||
}
|
||
|
||
dp[2 * k as usize]
|
||
}
|
||
}
|
||
```
|
||
|
||
|
||
|
||
|