mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2026-02-02 18:39:09 +08:00
901 lines
33 KiB
Markdown
901 lines
33 KiB
Markdown
<p align="center">
|
||
<a href="https://mp.weixin.qq.com/s/RsdcQ9umo09R6cfnwXZlrQ"><img src="https://img.shields.io/badge/PDF下载-代码随想录-blueviolet" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a>
|
||
<a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||
</p>
|
||
<p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
|
||
看完本文,可以一起解决如下两道题目
|
||
|
||
* 106.从中序与后序遍历序列构造二叉树
|
||
* 105.从前序与中序遍历序列构造二叉树
|
||
|
||
# 106.从中序与后序遍历序列构造二叉树
|
||
|
||
[力扣题目链接](https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/)
|
||
|
||
根据一棵树的中序遍历与后序遍历构造二叉树。
|
||
|
||
注意:
|
||
你可以假设树中没有重复的元素。
|
||
|
||
例如,给出
|
||
|
||
中序遍历 inorder = [9,3,15,20,7]
|
||
后序遍历 postorder = [9,15,7,20,3]
|
||
返回如下的二叉树:
|
||
|
||

|
||
|
||
## 思路
|
||
|
||
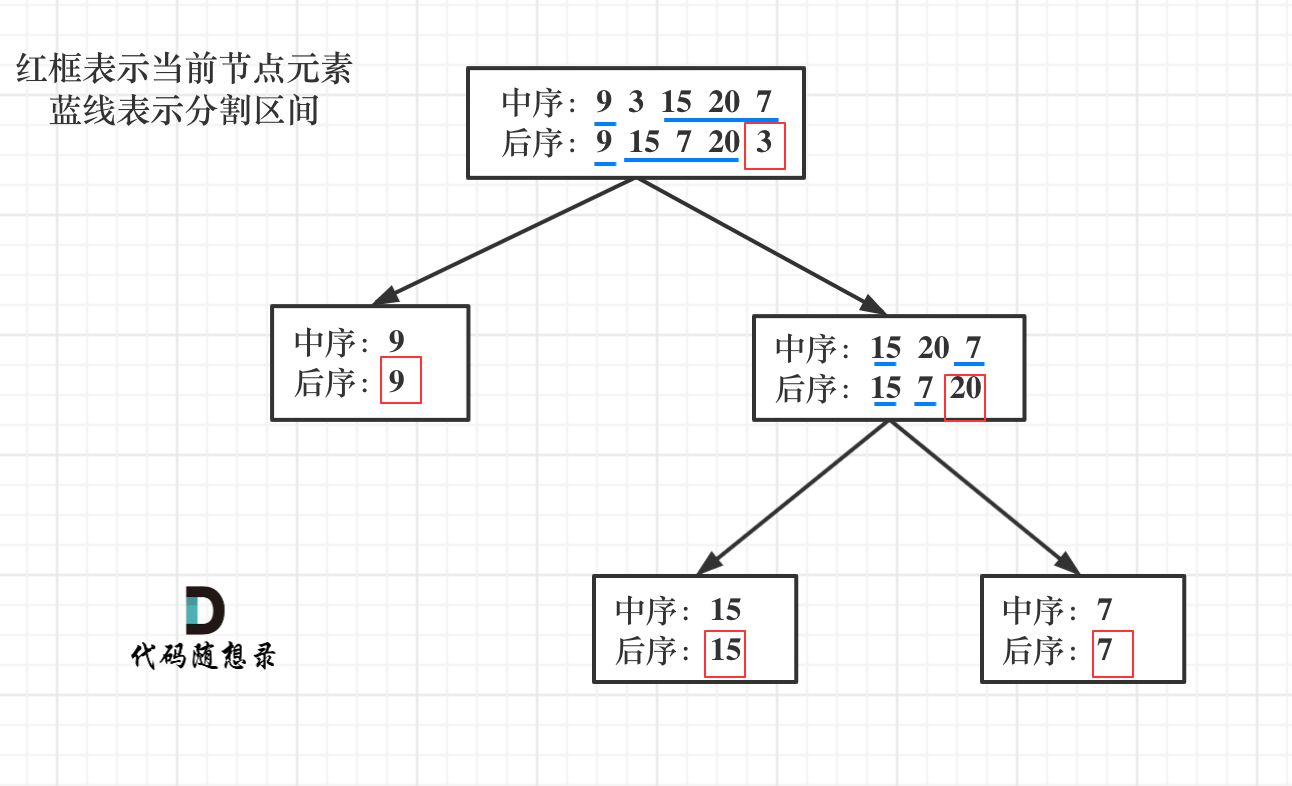
首先回忆一下如何根据两个顺序构造一个唯一的二叉树,相信理论知识大家应该都清楚,就是以 后序数组的最后一个元素为切割点,先切中序数组,根据中序数组,反过来在切后序数组。一层一层切下去,每次后序数组最后一个元素就是节点元素。
|
||
|
||
如果让我们肉眼看两个序列,画一颗二叉树的话,应该分分钟都可以画出来。
|
||
|
||
流程如图:
|
||
|
||
|
||
|
||
那么代码应该怎么写呢?
|
||
|
||
说到一层一层切割,就应该想到了递归。
|
||
|
||
来看一下一共分几步:
|
||
|
||
* 第一步:如果数组大小为零的话,说明是空节点了。
|
||
|
||
* 第二步:如果不为空,那么取后序数组最后一个元素作为节点元素。
|
||
|
||
* 第三步:找到后序数组最后一个元素在中序数组的位置,作为切割点
|
||
|
||
* 第四步:切割中序数组,切成中序左数组和中序右数组 (顺序别搞反了,一定是先切中序数组)
|
||
|
||
* 第五步:切割后序数组,切成后序左数组和后序右数组
|
||
|
||
* 第六步:递归处理左区间和右区间
|
||
|
||
不难写出如下代码:(先把框架写出来)
|
||
|
||
```CPP
|
||
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
|
||
|
||
// 第一步
|
||
if (postorder.size() == 0) return NULL;
|
||
|
||
// 第二步:后序遍历数组最后一个元素,就是当前的中间节点
|
||
int rootValue = postorder[postorder.size() - 1];
|
||
TreeNode* root = new TreeNode(rootValue);
|
||
|
||
// 叶子节点
|
||
if (postorder.size() == 1) return root;
|
||
|
||
// 第三步:找切割点
|
||
int delimiterIndex;
|
||
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
|
||
if (inorder[delimiterIndex] == rootValue) break;
|
||
}
|
||
|
||
// 第四步:切割中序数组,得到 中序左数组和中序右数组
|
||
// 第五步:切割后序数组,得到 后序左数组和后序右数组
|
||
|
||
// 第六步
|
||
root->left = traversal(中序左数组, 后序左数组);
|
||
root->right = traversal(中序右数组, 后序右数组);
|
||
|
||
return root;
|
||
}
|
||
```
|
||
|
||
**难点大家应该发现了,就是如何切割,以及边界值找不好很容易乱套。**
|
||
|
||
此时应该注意确定切割的标准,是左闭右开,还有左开又闭,还是左闭又闭,这个就是不变量,要在递归中保持这个不变量。
|
||
|
||
**在切割的过程中会产生四个区间,把握不好不变量的话,一会左闭右开,一会左闭又闭,必然乱套!**
|
||
|
||
我在[数组:每次遇到二分法,都是一看就会,一写就废](https://programmercarl.com/0035.搜索插入位置.html)和[数组:这个循环可以转懵很多人!](https://programmercarl.com/0059.螺旋矩阵II.html)中都强调过循环不变量的重要性,在二分查找以及螺旋矩阵的求解中,坚持循环不变量非常重要,本题也是。
|
||
|
||
|
||
首先要切割中序数组,为什么先切割中序数组呢?
|
||
|
||
切割点在后序数组的最后一个元素,就是用这个元素来切割中序数组的,所以必要先切割中序数组。
|
||
|
||
中序数组相对比较好切,找到切割点(后序数组的最后一个元素)在中序数组的位置,然后切割,如下代码中我坚持左闭右开的原则:
|
||
|
||
|
||
```C++
|
||
// 找到中序遍历的切割点
|
||
int delimiterIndex;
|
||
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
|
||
if (inorder[delimiterIndex] == rootValue) break;
|
||
}
|
||
|
||
// 左闭右开区间:[0, delimiterIndex)
|
||
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
|
||
// [delimiterIndex + 1, end)
|
||
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
|
||
```
|
||
|
||
接下来就要切割后序数组了。
|
||
|
||
首先后序数组的最后一个元素指定不能要了,这是切割点 也是 当前二叉树中间节点的元素,已经用了。
|
||
|
||
后序数组的切割点怎么找?
|
||
|
||
后序数组没有明确的切割元素来进行左右切割,不像中序数组有明确的切割点,切割点左右分开就可以了。
|
||
|
||
**此时有一个很重的点,就是中序数组大小一定是和后序数组的大小相同的(这是必然)。**
|
||
|
||
中序数组我们都切成了左中序数组和右中序数组了,那么后序数组就可以按照左中序数组的大小来切割,切成左后序数组和右后序数组。
|
||
|
||
代码如下:
|
||
|
||
```
|
||
// postorder 舍弃末尾元素,因为这个元素就是中间节点,已经用过了
|
||
postorder.resize(postorder.size() - 1);
|
||
|
||
// 左闭右开,注意这里使用了左中序数组大小作为切割点:[0, leftInorder.size)
|
||
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
|
||
// [leftInorder.size(), end)
|
||
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
|
||
```
|
||
|
||
此时,中序数组切成了左中序数组和右中序数组,后序数组切割成左后序数组和右后序数组。
|
||
|
||
接下来可以递归了,代码如下:
|
||
|
||
```
|
||
root->left = traversal(leftInorder, leftPostorder);
|
||
root->right = traversal(rightInorder, rightPostorder);
|
||
```
|
||
|
||
完整代码如下:
|
||
|
||
### C++完整代码
|
||
|
||
```CPP
|
||
class Solution {
|
||
private:
|
||
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
|
||
if (postorder.size() == 0) return NULL;
|
||
|
||
// 后序遍历数组最后一个元素,就是当前的中间节点
|
||
int rootValue = postorder[postorder.size() - 1];
|
||
TreeNode* root = new TreeNode(rootValue);
|
||
|
||
// 叶子节点
|
||
if (postorder.size() == 1) return root;
|
||
|
||
// 找到中序遍历的切割点
|
||
int delimiterIndex;
|
||
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
|
||
if (inorder[delimiterIndex] == rootValue) break;
|
||
}
|
||
|
||
// 切割中序数组
|
||
// 左闭右开区间:[0, delimiterIndex)
|
||
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
|
||
// [delimiterIndex + 1, end)
|
||
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
|
||
|
||
// postorder 舍弃末尾元素
|
||
postorder.resize(postorder.size() - 1);
|
||
|
||
// 切割后序数组
|
||
// 依然左闭右开,注意这里使用了左中序数组大小作为切割点
|
||
// [0, leftInorder.size)
|
||
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
|
||
// [leftInorder.size(), end)
|
||
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
|
||
|
||
root->left = traversal(leftInorder, leftPostorder);
|
||
root->right = traversal(rightInorder, rightPostorder);
|
||
|
||
return root;
|
||
}
|
||
public:
|
||
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
|
||
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
|
||
return traversal(inorder, postorder);
|
||
}
|
||
};
|
||
|
||
```
|
||
|
||
相信大家自己就算是思路清晰, 代码写出来一定是各种问题,所以一定要加日志来调试,看看是不是按照自己思路来切割的,不要大脑模拟,那样越想越糊涂。
|
||
|
||
加了日志的代码如下:(加了日志的代码不要在leetcode上提交,容易超时)
|
||
|
||
|
||
```CPP
|
||
class Solution {
|
||
private:
|
||
TreeNode* traversal (vector<int>& inorder, vector<int>& postorder) {
|
||
if (postorder.size() == 0) return NULL;
|
||
|
||
int rootValue = postorder[postorder.size() - 1];
|
||
TreeNode* root = new TreeNode(rootValue);
|
||
|
||
if (postorder.size() == 1) return root;
|
||
|
||
int delimiterIndex;
|
||
for (delimiterIndex = 0; delimiterIndex < inorder.size(); delimiterIndex++) {
|
||
if (inorder[delimiterIndex] == rootValue) break;
|
||
}
|
||
|
||
vector<int> leftInorder(inorder.begin(), inorder.begin() + delimiterIndex);
|
||
vector<int> rightInorder(inorder.begin() + delimiterIndex + 1, inorder.end() );
|
||
|
||
postorder.resize(postorder.size() - 1);
|
||
|
||
vector<int> leftPostorder(postorder.begin(), postorder.begin() + leftInorder.size());
|
||
vector<int> rightPostorder(postorder.begin() + leftInorder.size(), postorder.end());
|
||
|
||
// 一下为日志
|
||
cout << "----------" << endl;
|
||
|
||
cout << "leftInorder :";
|
||
for (int i : leftInorder) {
|
||
cout << i << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
cout << "rightInorder :";
|
||
for (int i : rightInorder) {
|
||
cout << i << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
cout << "leftPostorder :";
|
||
for (int i : leftPostorder) {
|
||
cout << i << " ";
|
||
}
|
||
cout << endl;
|
||
cout << "rightPostorder :";
|
||
for (int i : rightPostorder) {
|
||
cout << i << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
root->left = traversal(leftInorder, leftPostorder);
|
||
root->right = traversal(rightInorder, rightPostorder);
|
||
|
||
return root;
|
||
}
|
||
public:
|
||
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
|
||
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
|
||
return traversal(inorder, postorder);
|
||
}
|
||
};
|
||
```
|
||
|
||
**此时应该发现了,如上的代码性能并不好,应为每层递归定定义了新的vector(就是数组),既耗时又耗空间,但上面的代码是最好理解的,为了方便读者理解,所以用如上的代码来讲解。**
|
||
|
||
下面给出用下表索引写出的代码版本:(思路是一样的,只不过不用重复定义vector了,每次用下表索引来分割)
|
||
|
||
### C++优化版本
|
||
```CPP
|
||
class Solution {
|
||
private:
|
||
// 中序区间:[inorderBegin, inorderEnd),后序区间[postorderBegin, postorderEnd)
|
||
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
|
||
if (postorderBegin == postorderEnd) return NULL;
|
||
|
||
int rootValue = postorder[postorderEnd - 1];
|
||
TreeNode* root = new TreeNode(rootValue);
|
||
|
||
if (postorderEnd - postorderBegin == 1) return root;
|
||
|
||
int delimiterIndex;
|
||
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
|
||
if (inorder[delimiterIndex] == rootValue) break;
|
||
}
|
||
// 切割中序数组
|
||
// 左中序区间,左闭右开[leftInorderBegin, leftInorderEnd)
|
||
int leftInorderBegin = inorderBegin;
|
||
int leftInorderEnd = delimiterIndex;
|
||
// 右中序区间,左闭右开[rightInorderBegin, rightInorderEnd)
|
||
int rightInorderBegin = delimiterIndex + 1;
|
||
int rightInorderEnd = inorderEnd;
|
||
|
||
// 切割后序数组
|
||
// 左后序区间,左闭右开[leftPostorderBegin, leftPostorderEnd)
|
||
int leftPostorderBegin = postorderBegin;
|
||
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
|
||
// 右后序区间,左闭右开[rightPostorderBegin, rightPostorderEnd)
|
||
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
|
||
int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素,已经作为节点了
|
||
|
||
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
|
||
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
|
||
|
||
return root;
|
||
}
|
||
public:
|
||
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
|
||
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
|
||
// 左闭右开的原则
|
||
return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
|
||
}
|
||
};
|
||
```
|
||
|
||
那么这个版本写出来依然要打日志进行调试,打日志的版本如下:(**该版本不要在leetcode上提交,容易超时**)
|
||
|
||
```CPP
|
||
class Solution {
|
||
private:
|
||
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& postorder, int postorderBegin, int postorderEnd) {
|
||
if (postorderBegin == postorderEnd) return NULL;
|
||
|
||
int rootValue = postorder[postorderEnd - 1];
|
||
TreeNode* root = new TreeNode(rootValue);
|
||
|
||
if (postorderEnd - postorderBegin == 1) return root;
|
||
|
||
int delimiterIndex;
|
||
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
|
||
if (inorder[delimiterIndex] == rootValue) break;
|
||
}
|
||
// 切割中序数组
|
||
// 左中序区间,左闭右开[leftInorderBegin, leftInorderEnd)
|
||
int leftInorderBegin = inorderBegin;
|
||
int leftInorderEnd = delimiterIndex;
|
||
// 右中序区间,左闭右开[rightInorderBegin, rightInorderEnd)
|
||
int rightInorderBegin = delimiterIndex + 1;
|
||
int rightInorderEnd = inorderEnd;
|
||
|
||
// 切割后序数组
|
||
// 左后序区间,左闭右开[leftPostorderBegin, leftPostorderEnd)
|
||
int leftPostorderBegin = postorderBegin;
|
||
int leftPostorderEnd = postorderBegin + delimiterIndex - inorderBegin; // 终止位置是 需要加上 中序区间的大小size
|
||
// 右后序区间,左闭右开[rightPostorderBegin, rightPostorderEnd)
|
||
int rightPostorderBegin = postorderBegin + (delimiterIndex - inorderBegin);
|
||
int rightPostorderEnd = postorderEnd - 1; // 排除最后一个元素,已经作为节点了
|
||
|
||
cout << "----------" << endl;
|
||
cout << "leftInorder :";
|
||
for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
|
||
cout << inorder[i] << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
cout << "rightInorder :";
|
||
for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
|
||
cout << inorder[i] << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
cout << "leftpostorder :";
|
||
for (int i = leftPostorderBegin; i < leftPostorderEnd; i++) {
|
||
cout << postorder[i] << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
cout << "rightpostorder :";
|
||
for (int i = rightPostorderBegin; i < rightPostorderEnd; i++) {
|
||
cout << postorder[i] << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, postorder, leftPostorderBegin, leftPostorderEnd);
|
||
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, postorder, rightPostorderBegin, rightPostorderEnd);
|
||
|
||
return root;
|
||
}
|
||
public:
|
||
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
|
||
if (inorder.size() == 0 || postorder.size() == 0) return NULL;
|
||
return traversal(inorder, 0, inorder.size(), postorder, 0, postorder.size());
|
||
}
|
||
};
|
||
```
|
||
|
||
# 105.从前序与中序遍历序列构造二叉树
|
||
|
||
[力扣题目链接](https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/)
|
||
|
||
根据一棵树的前序遍历与中序遍历构造二叉树。
|
||
|
||
注意:
|
||
你可以假设树中没有重复的元素。
|
||
|
||
例如,给出
|
||
|
||
前序遍历 preorder = [3,9,20,15,7]
|
||
中序遍历 inorder = [9,3,15,20,7]
|
||
返回如下的二叉树:
|
||
|
||

|
||
|
||
## 思路
|
||
|
||
本题和106是一样的道理。
|
||
|
||
我就直接给出代码了。
|
||
|
||
带日志的版本C++代码如下: (**带日志的版本仅用于调试,不要在leetcode上提交,会超时**)
|
||
|
||
```CPP
|
||
class Solution {
|
||
private:
|
||
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
|
||
if (preorderBegin == preorderEnd) return NULL;
|
||
|
||
int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
|
||
TreeNode* root = new TreeNode(rootValue);
|
||
|
||
if (preorderEnd - preorderBegin == 1) return root;
|
||
|
||
int delimiterIndex;
|
||
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
|
||
if (inorder[delimiterIndex] == rootValue) break;
|
||
}
|
||
// 切割中序数组
|
||
// 中序左区间,左闭右开[leftInorderBegin, leftInorderEnd)
|
||
int leftInorderBegin = inorderBegin;
|
||
int leftInorderEnd = delimiterIndex;
|
||
// 中序右区间,左闭右开[rightInorderBegin, rightInorderEnd)
|
||
int rightInorderBegin = delimiterIndex + 1;
|
||
int rightInorderEnd = inorderEnd;
|
||
|
||
// 切割前序数组
|
||
// 前序左区间,左闭右开[leftPreorderBegin, leftPreorderEnd)
|
||
int leftPreorderBegin = preorderBegin + 1;
|
||
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
|
||
// 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
|
||
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
|
||
int rightPreorderEnd = preorderEnd;
|
||
|
||
cout << "----------" << endl;
|
||
cout << "leftInorder :";
|
||
for (int i = leftInorderBegin; i < leftInorderEnd; i++) {
|
||
cout << inorder[i] << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
cout << "rightInorder :";
|
||
for (int i = rightInorderBegin; i < rightInorderEnd; i++) {
|
||
cout << inorder[i] << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
cout << "leftPreorder :";
|
||
for (int i = leftPreorderBegin; i < leftPreorderEnd; i++) {
|
||
cout << preorder[i] << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
cout << "rightPreorder :";
|
||
for (int i = rightPreorderBegin; i < rightPreorderEnd; i++) {
|
||
cout << preorder[i] << " ";
|
||
}
|
||
cout << endl;
|
||
|
||
|
||
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, preorder, leftPreorderBegin, leftPreorderEnd);
|
||
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
|
||
|
||
return root;
|
||
}
|
||
|
||
public:
|
||
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
|
||
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
|
||
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
|
||
|
||
}
|
||
};
|
||
```
|
||
|
||
105.从前序与中序遍历序列构造二叉树,最后版本,C++代码:
|
||
|
||
```CPP
|
||
class Solution {
|
||
private:
|
||
TreeNode* traversal (vector<int>& inorder, int inorderBegin, int inorderEnd, vector<int>& preorder, int preorderBegin, int preorderEnd) {
|
||
if (preorderBegin == preorderEnd) return NULL;
|
||
|
||
int rootValue = preorder[preorderBegin]; // 注意用preorderBegin 不要用0
|
||
TreeNode* root = new TreeNode(rootValue);
|
||
|
||
if (preorderEnd - preorderBegin == 1) return root;
|
||
|
||
int delimiterIndex;
|
||
for (delimiterIndex = inorderBegin; delimiterIndex < inorderEnd; delimiterIndex++) {
|
||
if (inorder[delimiterIndex] == rootValue) break;
|
||
}
|
||
// 切割中序数组
|
||
// 中序左区间,左闭右开[leftInorderBegin, leftInorderEnd)
|
||
int leftInorderBegin = inorderBegin;
|
||
int leftInorderEnd = delimiterIndex;
|
||
// 中序右区间,左闭右开[rightInorderBegin, rightInorderEnd)
|
||
int rightInorderBegin = delimiterIndex + 1;
|
||
int rightInorderEnd = inorderEnd;
|
||
|
||
// 切割前序数组
|
||
// 前序左区间,左闭右开[leftPreorderBegin, leftPreorderEnd)
|
||
int leftPreorderBegin = preorderBegin + 1;
|
||
int leftPreorderEnd = preorderBegin + 1 + delimiterIndex - inorderBegin; // 终止位置是起始位置加上中序左区间的大小size
|
||
// 前序右区间, 左闭右开[rightPreorderBegin, rightPreorderEnd)
|
||
int rightPreorderBegin = preorderBegin + 1 + (delimiterIndex - inorderBegin);
|
||
int rightPreorderEnd = preorderEnd;
|
||
|
||
root->left = traversal(inorder, leftInorderBegin, leftInorderEnd, preorder, leftPreorderBegin, leftPreorderEnd);
|
||
root->right = traversal(inorder, rightInorderBegin, rightInorderEnd, preorder, rightPreorderBegin, rightPreorderEnd);
|
||
|
||
return root;
|
||
}
|
||
|
||
public:
|
||
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
|
||
if (inorder.size() == 0 || preorder.size() == 0) return NULL;
|
||
|
||
// 参数坚持左闭右开的原则
|
||
return traversal(inorder, 0, inorder.size(), preorder, 0, preorder.size());
|
||
}
|
||
};
|
||
```
|
||
|
||
# 思考题
|
||
|
||
前序和中序可以唯一确定一颗二叉树。
|
||
|
||
后序和中序可以唯一确定一颗二叉树。
|
||
|
||
那么前序和后序可不可以唯一确定一颗二叉树呢?
|
||
|
||
**前序和后序不能唯一确定一颗二叉树!**,因为没有中序遍历无法确定左右部分,也就是无法分割。
|
||
|
||
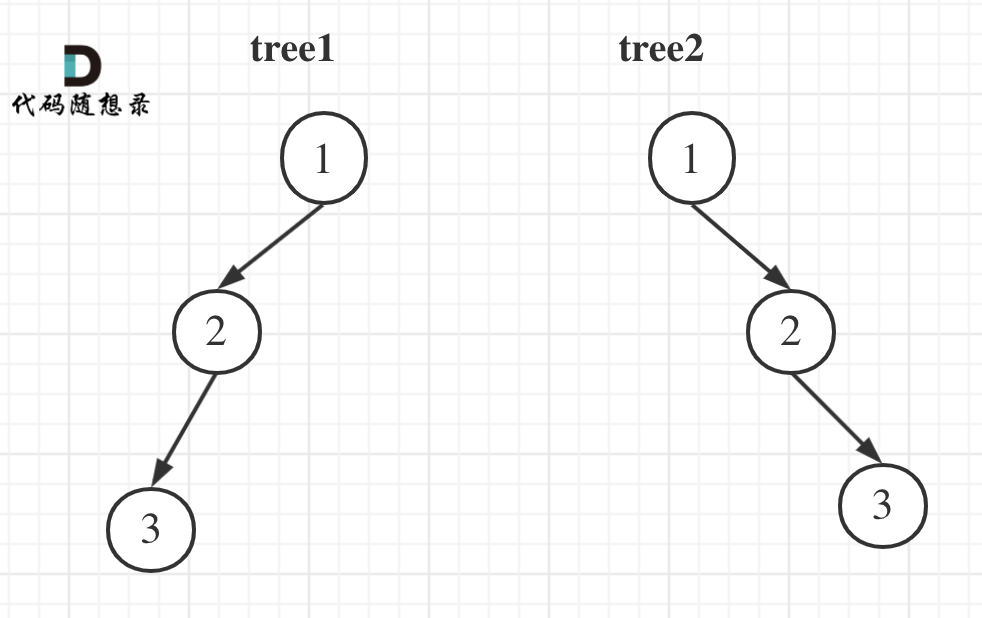
举一个例子:
|
||
|
||
|
||
|
||
tree1 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
|
||
|
||
tree2 的前序遍历是[1 2 3], 后序遍历是[3 2 1]。
|
||
|
||
那么tree1 和 tree2 的前序和后序完全相同,这是一棵树么,很明显是两棵树!
|
||
|
||
所以前序和后序不能唯一确定一颗二叉树!
|
||
|
||
# 总结
|
||
|
||
之前我们讲的二叉树题目都是各种遍历二叉树,这次开始构造二叉树了,思路其实比较简单,但是真正代码实现出来并不容易。
|
||
|
||
所以要避免眼高手低,踏实的把代码写出来。
|
||
|
||
我同时给出了添加日志的代码版本,因为这种题目是不太容易写出来调一调就能过的,所以一定要把流程日志打出来,看看符不符合自己的思路。
|
||
|
||
大家遇到这种题目的时候,也要学会打日志来调试(如何打日志有时候也是个技术活),不要脑动模拟,脑动模拟很容易越想越乱。
|
||
|
||
最后我还给出了为什么前序和中序可以唯一确定一颗二叉树,后序和中序可以唯一确定一颗二叉树,而前序和后序却不行。
|
||
|
||
认真研究完本篇,相信大家对二叉树的构造会清晰很多。
|
||
|
||
|
||
|
||
# 其他语言版本
|
||
|
||
## Java
|
||
|
||
106.从中序与后序遍历序列构造二叉树
|
||
|
||
```java
|
||
class Solution {
|
||
public TreeNode buildTree(int[] inorder, int[] postorder) {
|
||
return buildTree1(inorder, 0, inorder.length, postorder, 0, postorder.length);
|
||
}
|
||
public TreeNode buildTree1(int[] inorder, int inLeft, int inRight,
|
||
int[] postorder, int postLeft, int postRight) {
|
||
// 没有元素了
|
||
if (inRight - inLeft < 1) {
|
||
return null;
|
||
}
|
||
// 只有一个元素了
|
||
if (inRight - inLeft == 1) {
|
||
return new TreeNode(inorder[inLeft]);
|
||
}
|
||
// 后序数组postorder里最后一个即为根结点
|
||
int rootVal = postorder[postRight - 1];
|
||
TreeNode root = new TreeNode(rootVal);
|
||
int rootIndex = 0;
|
||
// 根据根结点的值找到该值在中序数组inorder里的位置
|
||
for (int i = inLeft; i < inRight; i++) {
|
||
if (inorder[i] == rootVal) {
|
||
rootIndex = i;
|
||
}
|
||
}
|
||
// 根据rootIndex划分左右子树
|
||
root.left = buildTree1(inorder, inLeft, rootIndex,
|
||
postorder, postLeft, postLeft + (rootIndex - inLeft));
|
||
root.right = buildTree1(inorder, rootIndex + 1, inRight,
|
||
postorder, postLeft + (rootIndex - inLeft), postRight - 1);
|
||
return root;
|
||
}
|
||
}
|
||
```
|
||
|
||
105.从前序与中序遍历序列构造二叉树
|
||
|
||
```java
|
||
class Solution {
|
||
public TreeNode buildTree(int[] preorder, int[] inorder) {
|
||
return helper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1);
|
||
}
|
||
|
||
public TreeNode helper(int[] preorder, int preLeft, int preRight,
|
||
int[] inorder, int inLeft, int inRight) {
|
||
// 递归终止条件
|
||
if (inLeft > inRight || preLeft > preRight) return null;
|
||
|
||
// val 为前序遍历第一个的值,也即是根节点的值
|
||
// idx 为根据根节点的值来找中序遍历的下标
|
||
int idx = inLeft, val = preorder[preLeft];
|
||
TreeNode root = new TreeNode(val);
|
||
for (int i = inLeft; i <= inRight; i++) {
|
||
if (inorder[i] == val) {
|
||
idx = i;
|
||
break;
|
||
}
|
||
}
|
||
|
||
// 根据 idx 来递归找左右子树
|
||
root.left = helper(preorder, preLeft + 1, preLeft + (idx - inLeft),
|
||
inorder, inLeft, idx - 1);
|
||
root.right = helper(preorder, preLeft + (idx - inLeft) + 1, preRight,
|
||
inorder, idx + 1, inRight);
|
||
return root;
|
||
}
|
||
}
|
||
```
|
||
|
||
## Python
|
||
|
||
105.从前序与中序遍历序列构造二叉树
|
||
|
||
```python
|
||
class Solution:
|
||
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
|
||
# 第一步: 特殊情况讨论: 树为空. 或者说是递归终止条件
|
||
if not preorder:
|
||
return None
|
||
|
||
# 第二步: 前序遍历的第一个就是当前的中间节点.
|
||
root_val = preorder[0]
|
||
root = TreeNode(root_val)
|
||
|
||
# 第三步: 找切割点.
|
||
separator_idx = inorder.index(root_val)
|
||
|
||
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
|
||
inorder_left = inorder[:separator_idx]
|
||
inorder_right = inorder[separator_idx + 1:]
|
||
|
||
# 第五步: 切割preorder数组. 得到preorder数组的左,右半边.
|
||
# ⭐️ 重点1: 中序数组大小一定跟前序数组大小是相同的.
|
||
preorder_left = preorder[1:1 + len(inorder_left)]
|
||
preorder_right = preorder[1 + len(inorder_left):]
|
||
|
||
# 第六步: 递归
|
||
root.left = self.buildTree(preorder_left, inorder_left)
|
||
root.right = self.buildTree(preorder_right, inorder_right)
|
||
|
||
return root
|
||
```
|
||
|
||
106.从中序与后序遍历序列构造二叉树
|
||
|
||
```python
|
||
class Solution:
|
||
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
|
||
# 第一步: 特殊情况讨论: 树为空. (递归终止条件)
|
||
if not postorder:
|
||
return None
|
||
|
||
# 第二步: 后序遍历的最后一个就是当前的中间节点.
|
||
root_val = postorder[-1]
|
||
root = TreeNode(root_val)
|
||
|
||
# 第三步: 找切割点.
|
||
separator_idx = inorder.index(root_val)
|
||
|
||
# 第四步: 切割inorder数组. 得到inorder数组的左,右半边.
|
||
inorder_left = inorder[:separator_idx]
|
||
inorder_right = inorder[separator_idx + 1:]
|
||
|
||
# 第五步: 切割postorder数组. 得到postorder数组的左,右半边.
|
||
# ⭐️ 重点1: 中序数组大小一定跟后序数组大小是相同的.
|
||
postorder_left = postorder[:len(inorder_left)]
|
||
postorder_right = postorder[len(inorder_left): len(postorder) - 1]
|
||
|
||
# 第六步: 递归
|
||
root.left = self.buildTree(inorder_left, postorder_left)
|
||
root.right = self.buildTree(inorder_right, postorder_right)
|
||
|
||
return root
|
||
```
|
||
|
||
## Go
|
||
|
||
106 从中序与后序遍历序列构造二叉树
|
||
|
||
```go
|
||
/**
|
||
* Definition for a binary tree node.
|
||
* type TreeNode struct {
|
||
* Val int
|
||
* Left *TreeNode
|
||
* Right *TreeNode
|
||
* }
|
||
*/
|
||
func buildTree(inorder []int, postorder []int) *TreeNode {
|
||
if len(inorder)<1||len(postorder)<1{return nil}
|
||
//先找到根节点(后续遍历的最后一个就是根节点)
|
||
nodeValue:=postorder[len(postorder)-1]
|
||
//从中序遍历中找到一分为二的点,左边为左子树,右边为右子树
|
||
left:=findRootIndex(inorder,nodeValue)
|
||
//构造root
|
||
root:=&TreeNode{Val: nodeValue,
|
||
Left: buildTree(inorder[:left],postorder[:left]),//将后续遍历一分为二,左边为左子树,右边为右子树
|
||
Right: buildTree(inorder[left+1:],postorder[left:len(postorder)-1])}
|
||
return root
|
||
}
|
||
func findRootIndex(inorder []int,target int) (index int){
|
||
for i:=0;i<len(inorder);i++{
|
||
if target==inorder[i]{
|
||
return i
|
||
}
|
||
}
|
||
return -1
|
||
}
|
||
```
|
||
|
||
105 从前序与中序遍历序列构造二叉树
|
||
|
||
```go
|
||
/**
|
||
* Definition for a binary tree node.
|
||
* type TreeNode struct {
|
||
* Val int
|
||
* Left *TreeNode
|
||
* Right *TreeNode
|
||
* }
|
||
*/
|
||
func buildTree(preorder []int, inorder []int) *TreeNode {
|
||
if len(preorder)<1||len(inorder)<1{return nil}
|
||
left:=findRootIndex(preorder[0],inorder)
|
||
root:=&TreeNode{
|
||
Val: preorder[0],
|
||
Left: buildTree(preorder[1:left+1],inorder[:left]),
|
||
Right: buildTree(preorder[left+1:],inorder[left+1:])}
|
||
return root
|
||
}
|
||
func findRootIndex(target int,inorder []int) int{
|
||
for i:=0;i<len(inorder);i++{
|
||
if target==inorder[i]{
|
||
return i
|
||
}
|
||
}
|
||
return -1
|
||
}
|
||
```
|
||
|
||
|
||
|
||
|
||
## JavaScript
|
||
|
||
```javascript
|
||
var buildTree = function(inorder, postorder) {
|
||
if (!postorder.length) return null
|
||
|
||
let root = new TreeNode(postorder[postorder.length - 1])
|
||
|
||
let index = inorder.findIndex(number => number === root.val)
|
||
|
||
root.left = buildTree(inorder.slice(0, index), postorder.slice(0, index))
|
||
root.right = buildTree(inorder.slice(index + 1, inorder.length), postorder.slice(index, postorder.length - 1))
|
||
|
||
return root
|
||
};
|
||
```
|
||
|
||
从前序与中序遍历序列构造二叉树
|
||
|
||
```javascript
|
||
var buildTree = function(preorder, inorder) {
|
||
if(!preorder.length)
|
||
return null;
|
||
let root = new TreeNode(preorder[0]);
|
||
let mid = inorder.findIndex((number) => number === root.val);
|
||
root.left = buildTree(preorder.slice(1, mid + 1), inorder.slice(0, mid));
|
||
root.right = buildTree(preorder.slice(mid + 1, preorder.length), inorder.slice(mid + 1, inorder.length));
|
||
return root;
|
||
};
|
||
```
|
||
|
||
## C
|
||
106 从中序与后序遍历序列构造二叉树
|
||
```c
|
||
int linearSearch(int* arr, int arrSize, int key) {
|
||
int i;
|
||
for(i = 0; i < arrSize; i++) {
|
||
if(arr[i] == key)
|
||
return i;
|
||
}
|
||
return -1;
|
||
}
|
||
|
||
struct TreeNode* buildTree(int* inorder, int inorderSize, int* postorder, int postorderSize){
|
||
//若中序遍历数组中没有元素,则返回NULL
|
||
if(!inorderSize)
|
||
return NULL;
|
||
//创建一个新的结点,将node的val设置为后序遍历的最后一个元素
|
||
struct TreeNode* node = (struct TreeNode*)malloc(sizeof(struct TreeNode));
|
||
node->val = postorder[postorderSize - 1];
|
||
|
||
//通过线性查找找到中间结点在中序数组中的位置
|
||
int index = linearSearch(inorder, inorderSize, postorder[postorderSize - 1]);
|
||
|
||
//左子树数组大小为index
|
||
//右子树的数组大小为数组大小减index减1(减的1为中间结点)
|
||
int rightSize = inorderSize - index - 1;
|
||
node->left = buildTree(inorder, index, postorder, index);
|
||
node->right = buildTree(inorder + index + 1, rightSize, postorder + index, rightSize);
|
||
return node;
|
||
}
|
||
```
|
||
|
||
105 从前序与中序遍历序列构造二叉树
|
||
```c
|
||
struct TreeNode* buildTree(int* preorder, int preorderSize, int* inorder, int inorderSize){
|
||
// 递归结束条件:传入的数组大小为0
|
||
if(!preorderSize)
|
||
return NULL;
|
||
|
||
// 1.找到前序遍历数组的第一个元素, 创建结点。左右孩子设置为NULL。
|
||
int rootValue = preorder[0];
|
||
struct TreeNode* root = (struct TreeNode*)malloc(sizeof(struct TreeNode));
|
||
root->val = rootValue;
|
||
root->left = NULL;
|
||
root->right = NULL;
|
||
|
||
// 2.若前序遍历数组的大小为1,返回该结点
|
||
if(preorderSize == 1)
|
||
return root;
|
||
|
||
// 3.根据该结点切割中序遍历数组,将中序遍历数组分割成左右两个数组。算出他们的各自大小
|
||
int index;
|
||
for(index = 0; index < inorderSize; index++) {
|
||
if(inorder[index] == rootValue)
|
||
break;
|
||
}
|
||
int leftNum = index;
|
||
int rightNum = inorderSize - index - 1;
|
||
|
||
int* leftInorder = inorder;
|
||
int* rightInorder = inorder + leftNum + 1;
|
||
|
||
// 4.根据中序遍历数组左右数组的各子大小切割前序遍历数组。也分为左右数组
|
||
int* leftPreorder = preorder+1;
|
||
int* rightPreorder = preorder + 1 + leftNum;
|
||
|
||
// 5.递归进入左右数组,将返回的结果作为根结点的左右孩子
|
||
root->left = buildTree(leftPreorder, leftNum, leftInorder, leftNum);
|
||
root->right = buildTree(rightPreorder, rightNum, rightInorder, rightNum);
|
||
|
||
// 6.返回根节点
|
||
return root;
|
||
}
|
||
```
|
||
|
||
-----------------------
|
||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
|
||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码.jpg width=450> </img></div>
|