mirror of
https://github.com/youngyangyang04/leetcode-master.git
synced 2026-02-02 18:39:09 +08:00
561 lines
14 KiB
Markdown
561 lines
14 KiB
Markdown
<p align="center">
|
||
<a href="https://mp.weixin.qq.com/s/RsdcQ9umo09R6cfnwXZlrQ"><img src="https://img.shields.io/badge/PDF下载-代码随想录-blueviolet" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw"><img src="https://img.shields.io/badge/刷题-微信群-green" alt=""></a>
|
||
<a href="https://space.bilibili.com/525438321"><img src="https://img.shields.io/badge/B站-代码随想录-orange" alt=""></a>
|
||
<a href="https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ"><img src="https://img.shields.io/badge/知识星球-代码随想录-blue" alt=""></a>
|
||
</p>
|
||
<p align="center"><strong>欢迎大家<a href="https://mp.weixin.qq.com/s/tqCxrMEU-ajQumL1i8im9A">参与本项目</a>,贡献其他语言版本的代码,拥抱开源,让更多学习算法的小伙伴们收益!</strong></p>
|
||
|
||
|
||
看完本篇可以一起做了如下两道题目:
|
||
|
||
* 104.二叉树的最大深度
|
||
* 559.n叉树的最大深度
|
||
|
||
# 104.二叉树的最大深度
|
||
|
||
[力扣题目链接](https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/)
|
||
|
||
给定一个二叉树,找出其最大深度。
|
||
|
||
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
|
||
|
||
说明: 叶子节点是指没有子节点的节点。
|
||
|
||
示例:
|
||
给定二叉树 [3,9,20,null,null,15,7],
|
||
|
||

|
||
|
||
返回它的最大深度 3 。
|
||
|
||
## 递归法
|
||
|
||
本题可以使用前序(中左右),也可以使用后序遍历(左右中),使用前序求的就是深度,使用后序求的是高度。
|
||
|
||
**而根节点的高度就是二叉树的最大深度**,所以本题中我们通过后序求的根节点高度来求的二叉树最大深度。
|
||
|
||
这一点其实是很多同学没有想清楚的,很多题解同样没有讲清楚。
|
||
|
||
我先用后序遍历(左右中)来计算树的高度。
|
||
|
||
1. 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回这棵树的深度,所以返回值为int类型。
|
||
|
||
代码如下:
|
||
```c++
|
||
int getdepth(treenode* node)
|
||
```
|
||
|
||
2. 确定终止条件:如果为空节点的话,就返回0,表示高度为0。
|
||
|
||
代码如下:
|
||
```c++
|
||
if (node == null) return 0;
|
||
```
|
||
|
||
3. 确定单层递归的逻辑:先求它的左子树的深度,再求的右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。
|
||
|
||
代码如下:
|
||
|
||
```c++
|
||
int leftdepth = getdepth(node->left); // 左
|
||
int rightdepth = getdepth(node->right); // 右
|
||
int depth = 1 + max(leftdepth, rightdepth); // 中
|
||
return depth;
|
||
```
|
||
|
||
所以整体c++代码如下:
|
||
|
||
```c++
|
||
class solution {
|
||
public:
|
||
int getdepth(treenode* node) {
|
||
if (node == null) return 0;
|
||
int leftdepth = getdepth(node->left); // 左
|
||
int rightdepth = getdepth(node->right); // 右
|
||
int depth = 1 + max(leftdepth, rightdepth); // 中
|
||
return depth;
|
||
}
|
||
int maxdepth(treenode* root) {
|
||
return getdepth(root);
|
||
}
|
||
};
|
||
```
|
||
|
||
代码精简之后c++代码如下:
|
||
```c++
|
||
class solution {
|
||
public:
|
||
int maxdepth(treenode* root) {
|
||
if (root == null) return 0;
|
||
return 1 + max(maxdepth(root->left), maxdepth(root->right));
|
||
}
|
||
};
|
||
|
||
```
|
||
|
||
**精简之后的代码根本看不出是哪种遍历方式,也看不出递归三部曲的步骤,所以如果对二叉树的操作还不熟练,尽量不要直接照着精简代码来学。**
|
||
|
||
|
||
本题当然也可以使用前序,代码如下:(**充分表现出求深度回溯的过程**)
|
||
|
||
```c++
|
||
class solution {
|
||
public:
|
||
int result;
|
||
void getdepth(treenode* node, int depth) {
|
||
result = depth > result ? depth : result; // 中
|
||
|
||
if (node->left == null && node->right == null) return ;
|
||
|
||
if (node->left) { // 左
|
||
depth++; // 深度+1
|
||
getdepth(node->left, depth);
|
||
depth--; // 回溯,深度-1
|
||
}
|
||
if (node->right) { // 右
|
||
depth++; // 深度+1
|
||
getdepth(node->right, depth);
|
||
depth--; // 回溯,深度-1
|
||
}
|
||
return ;
|
||
}
|
||
int maxdepth(treenode* root) {
|
||
result = 0;
|
||
if (root == 0) return result;
|
||
getdepth(root, 1);
|
||
return result;
|
||
}
|
||
};
|
||
```
|
||
|
||
**可以看出使用了前序(中左右)的遍历顺序,这才是真正求深度的逻辑!**
|
||
|
||
注意以上代码是为了把细节体现出来,简化一下代码如下:
|
||
|
||
```c++
|
||
class solution {
|
||
public:
|
||
int result;
|
||
void getdepth(treenode* node, int depth) {
|
||
result = depth > result ? depth : result; // 中
|
||
if (node->left == null && node->right == null) return ;
|
||
if (node->left) { // 左
|
||
getdepth(node->left, depth + 1);
|
||
}
|
||
if (node->right) { // 右
|
||
getdepth(node->right, depth + 1);
|
||
}
|
||
return ;
|
||
}
|
||
int maxdepth(treenode* root) {
|
||
result = 0;
|
||
if (root == 0) return result;
|
||
getdepth(root, 1);
|
||
return result;
|
||
}
|
||
};
|
||
```
|
||
|
||
## 迭代法
|
||
|
||
使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合。
|
||
|
||
在二叉树中,一层一层的来遍历二叉树,记录一下遍历的层数就是二叉树的深度,如图所示:
|
||
|
||
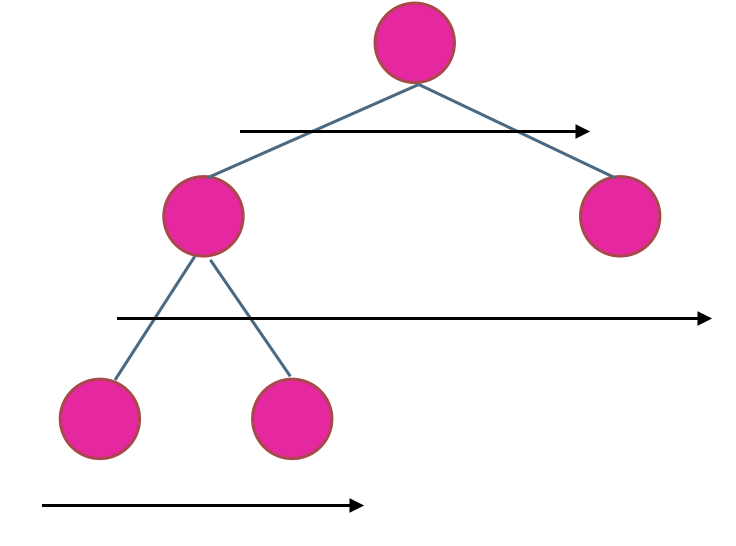
|
||
|
||
所以这道题的迭代法就是一道模板题,可以使用二叉树层序遍历的模板来解决的。
|
||
|
||
如果对层序遍历还不清楚的话,可以看这篇:[二叉树:层序遍历登场!](https://programmercarl.com/0102.二叉树的层序遍历.html)
|
||
|
||
c++代码如下:
|
||
|
||
```c++
|
||
class solution {
|
||
public:
|
||
int maxdepth(treenode* root) {
|
||
if (root == null) return 0;
|
||
int depth = 0;
|
||
queue<treenode*> que;
|
||
que.push(root);
|
||
while(!que.empty()) {
|
||
int size = que.size();
|
||
depth++; // 记录深度
|
||
for (int i = 0; i < size; i++) {
|
||
treenode* node = que.front();
|
||
que.pop();
|
||
if (node->left) que.push(node->left);
|
||
if (node->right) que.push(node->right);
|
||
}
|
||
}
|
||
return depth;
|
||
}
|
||
};
|
||
```
|
||
|
||
那么我们可以顺便解决一下n叉树的最大深度问题
|
||
|
||
# 559.n叉树的最大深度
|
||
|
||
[力扣题目链接](https://leetcode-cn.com/problems/maximum-depth-of-n-ary-tree/)
|
||
|
||
给定一个 n 叉树,找到其最大深度。
|
||
|
||
最大深度是指从根节点到最远叶子节点的最长路径上的节点总数。
|
||
|
||
例如,给定一个 3叉树 :
|
||
|
||

|
||
|
||
我们应返回其最大深度,3。
|
||
|
||
思路:
|
||
|
||
依然可以提供递归法和迭代法,来解决这个问题,思路是和二叉树思路一样的,直接给出代码如下:
|
||
|
||
## 递归法
|
||
|
||
c++代码:
|
||
|
||
```c++
|
||
class solution {
|
||
public:
|
||
int maxdepth(node* root) {
|
||
if (root == 0) return 0;
|
||
int depth = 0;
|
||
for (int i = 0; i < root->children.size(); i++) {
|
||
depth = max (depth, maxdepth(root->children[i]));
|
||
}
|
||
return depth + 1;
|
||
}
|
||
};
|
||
```
|
||
## 迭代法
|
||
|
||
依然是层序遍历,代码如下:
|
||
|
||
```c++
|
||
class solution {
|
||
public:
|
||
int maxdepth(node* root) {
|
||
queue<node*> que;
|
||
if (root != null) que.push(root);
|
||
int depth = 0;
|
||
while (!que.empty()) {
|
||
int size = que.size();
|
||
depth++; // 记录深度
|
||
for (int i = 0; i < size; i++) {
|
||
node* node = que.front();
|
||
que.pop();
|
||
for (int j = 0; j < node->children.size(); j++) {
|
||
if (node->children[j]) que.push(node->children[j]);
|
||
}
|
||
}
|
||
}
|
||
return depth;
|
||
}
|
||
};
|
||
```
|
||
|
||
# 其他语言版本
|
||
|
||
## java
|
||
|
||
### 104.二叉树的最大深度
|
||
|
||
```java
|
||
class solution {
|
||
/**
|
||
* 递归法
|
||
*/
|
||
public int maxdepth(treenode root) {
|
||
if (root == null) {
|
||
return 0;
|
||
}
|
||
int leftdepth = maxdepth(root.left);
|
||
int rightdepth = maxdepth(root.right);
|
||
return math.max(leftdepth, rightdepth) + 1;
|
||
|
||
}
|
||
}
|
||
```
|
||
|
||
```java
|
||
class solution {
|
||
/**
|
||
* 迭代法,使用层序遍历
|
||
*/
|
||
public int maxdepth(treenode root) {
|
||
if(root == null) {
|
||
return 0;
|
||
}
|
||
deque<treenode> deque = new linkedlist<>();
|
||
deque.offer(root);
|
||
int depth = 0;
|
||
while (!deque.isempty()) {
|
||
int size = deque.size();
|
||
depth++;
|
||
for (int i = 0; i < size; i++) {
|
||
treenode poll = deque.poll();
|
||
if (poll.left != null) {
|
||
deque.offer(poll.left);
|
||
}
|
||
if (poll.right != null) {
|
||
deque.offer(poll.right);
|
||
}
|
||
}
|
||
}
|
||
return depth;
|
||
}
|
||
}
|
||
```
|
||
|
||
## python
|
||
|
||
### 104.二叉树的最大深度
|
||
|
||
递归法:
|
||
```python
|
||
class solution:
|
||
def maxdepth(self, root: treenode) -> int:
|
||
return self.getdepth(root)
|
||
|
||
def getdepth(self, node):
|
||
if not node:
|
||
return 0
|
||
leftdepth = self.getdepth(node.left) #左
|
||
rightdepth = self.getdepth(node.right) #右
|
||
depth = 1 + max(leftdepth, rightdepth) #中
|
||
return depth
|
||
```
|
||
|
||
递归法:精简代码
|
||
```python
|
||
class solution:
|
||
def maxdepth(self, root: treenode) -> int:
|
||
if not root:
|
||
return 0
|
||
return 1 + max(self.maxdepth(root.left), self.maxdepth(root.right))
|
||
```
|
||
|
||
迭代法:
|
||
```python
|
||
import collections
|
||
class solution:
|
||
def maxdepth(self, root: treenode) -> int:
|
||
if not root:
|
||
return 0
|
||
depth = 0 #记录深度
|
||
queue = collections.deque()
|
||
queue.append(root)
|
||
while queue:
|
||
size = len(queue)
|
||
depth += 1
|
||
for i in range(size):
|
||
node = queue.popleft()
|
||
if node.left:
|
||
queue.append(node.left)
|
||
if node.right:
|
||
queue.append(node.right)
|
||
return depth
|
||
```
|
||
|
||
### 559.n叉树的最大深度
|
||
|
||
递归法:
|
||
```python
|
||
class solution:
|
||
def maxdepth(self, root: 'node') -> int:
|
||
if not root:
|
||
return 0
|
||
depth = 0
|
||
for i in range(len(root.children)):
|
||
depth = max(depth, self.maxdepth(root.children[i]))
|
||
return depth + 1
|
||
```
|
||
|
||
迭代法:
|
||
```python
|
||
import collections
|
||
class solution:
|
||
def maxdepth(self, root: 'node') -> int:
|
||
queue = collections.deque()
|
||
if root:
|
||
queue.append(root)
|
||
depth = 0 #记录深度
|
||
while queue:
|
||
size = len(queue)
|
||
depth += 1
|
||
for i in range(size):
|
||
node = queue.popleft()
|
||
for j in range(len(node.children)):
|
||
if node.children[j]:
|
||
queue.append(node.children[j])
|
||
return depth
|
||
```
|
||
|
||
使用栈来模拟后序遍历依然可以
|
||
```python
|
||
class solution:
|
||
def maxdepth(self, root: 'node') -> int:
|
||
st = []
|
||
if root:
|
||
st.append(root)
|
||
depth = 0
|
||
result = 0
|
||
while st:
|
||
node = st.pop()
|
||
if node != none:
|
||
st.append(node) #中
|
||
st.append(none)
|
||
depth += 1
|
||
for i in range(len(node.children)): #处理孩子
|
||
if node.children[i]:
|
||
st.append(node.children[i])
|
||
|
||
else:
|
||
node = st.pop()
|
||
depth -= 1
|
||
result = max(result, depth)
|
||
return result
|
||
```
|
||
|
||
|
||
## go
|
||
|
||
```go
|
||
/**
|
||
* definition for a binary tree node.
|
||
* type treenode struct {
|
||
* val int
|
||
* left *treenode
|
||
* right *treenode
|
||
* }
|
||
*/
|
||
func max (a, b int) int {
|
||
if a > b {
|
||
return a;
|
||
}
|
||
return b;
|
||
}
|
||
// 递归
|
||
func maxdepth(root *treenode) int {
|
||
if root == nil {
|
||
return 0;
|
||
}
|
||
return max(maxdepth(root.left), maxdepth(root.right)) + 1;
|
||
}
|
||
|
||
// 遍历
|
||
func maxdepth(root *treenode) int {
|
||
levl := 0;
|
||
queue := make([]*treenode, 0);
|
||
if root != nil {
|
||
queue = append(queue, root);
|
||
}
|
||
for l := len(queue); l > 0; {
|
||
for ;l > 0;l-- {
|
||
node := queue[0];
|
||
if node.left != nil {
|
||
queue = append(queue, node.left);
|
||
}
|
||
if node.right != nil {
|
||
queue = append(queue, node.right);
|
||
}
|
||
queue = queue[1:];
|
||
}
|
||
levl++;
|
||
l = len(queue);
|
||
}
|
||
return levl;
|
||
}
|
||
|
||
```
|
||
|
||
|
||
## javascript
|
||
|
||
```javascript
|
||
var maxdepth = function(root) {
|
||
if (!root) return root
|
||
return 1 + math.max(maxdepth(root.left), maxdepth(root.right))
|
||
};
|
||
```
|
||
|
||
二叉树最大深度递归遍历
|
||
```javascript
|
||
var maxdepth = function(root) {
|
||
//使用递归的方法 递归三部曲
|
||
//1. 确定递归函数的参数和返回值
|
||
const getdepth=function(node){
|
||
//2. 确定终止条件
|
||
if(node===null){
|
||
return 0;
|
||
}
|
||
//3. 确定单层逻辑
|
||
let leftdepth=getdepth(node.left);
|
||
let rightdepth=getdepth(node.right);
|
||
let depth=1+math.max(leftdepth,rightdepth);
|
||
return depth;
|
||
}
|
||
return getdepth(root);
|
||
};
|
||
```
|
||
|
||
二叉树最大深度层级遍历
|
||
```javascript
|
||
var maxDepth = function(root) {
|
||
if(!root) return 0
|
||
let count = 0
|
||
const queue = [root]
|
||
while(queue.length) {
|
||
let size = queue.length
|
||
/* 层数+1 */
|
||
count++
|
||
while(size--) {
|
||
let node = queue.shift();
|
||
node.left && queue.push(node.left);
|
||
node.right && queue.push(node.right);
|
||
}
|
||
}
|
||
return count
|
||
};
|
||
```
|
||
|
||
N叉树的最大深度 递归写法
|
||
```js
|
||
var maxDepth = function(root) {
|
||
if(!root) return 0
|
||
let depth = 0
|
||
for(let node of root.children) {
|
||
depth = Math.max(depth, maxDepth(node))
|
||
}
|
||
return depth + 1
|
||
}
|
||
```
|
||
|
||
N叉树的最大深度 层序遍历
|
||
```js
|
||
var maxDepth = function(root) {
|
||
if(!root) return 0
|
||
let count = 0
|
||
let queue = [root]
|
||
while(queue.length) {
|
||
let size = queue.length
|
||
count++
|
||
while(size--) {
|
||
let node = queue.shift()
|
||
node && (queue = [...queue, ...node.children])
|
||
}
|
||
}
|
||
return count
|
||
};
|
||
```
|
||
|
||
-----------------------
|
||
* 作者微信:[程序员Carl](https://mp.weixin.qq.com/s/b66DFkOp8OOxdZC_xLZxfw)
|
||
* B站视频:[代码随想录](https://space.bilibili.com/525438321)
|
||
* 知识星球:[代码随想录](https://mp.weixin.qq.com/s/QVF6upVMSbgvZy8lHZS3CQ)
|
||
<div align="center"><img src=https://code-thinking.cdn.bcebos.com/pics/01二维码.jpg width=450> </img></div>
|