2022-WangDao-CS-DS-Notes/6.5最小生成树(Prim算法、Kruskal算法).md

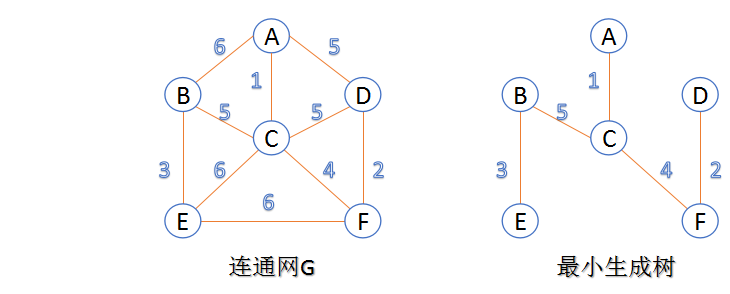
最小生成树

一、最小生成树的概念

连通图生成树，非连通图生成森林

生成树是包含图中全部顶点的一个极小连通子图 特性：图中有n个顶点，则它的生成树含有n-1条边。 去除一条边会变成非连通图；加上一条边会变成一个回路

之前学过广度优先生成树和深度优先生成树。

最小生成树，也叫最小代价树。在带权连通无向图的所有生成树中，所有边的代价和最小。

最小生成树可能很多，但边的权值之和总是唯一且最小的。

最小生成的边=顶点数-1

二、Prim算法（普利姆算法）

此算法可以称为“加点法”，每次迭代选择代价最小的边对应的点，加入到最小生成树中。算法从某一个顶点s开始，逐渐长大覆盖整个连通网的所有顶点。

实现思想：以最低代价加入点。 用两个数组： ①isJoin数组：标记各结点是否已加入树。 ②lowCost数组：各节点加入树的最低代价。

每轮遍历isJoin数组，第一遍找到lowCost最低的顶点，然后加入；第二遍循环遍历更新各点的lowCost值。 则时间复杂度=$$O(|V|^2)$$，适合边稠密图

三、Kruskal算法（克鲁斯卡尔算法）

此算法可以称为“加边法”，初始最小生成树边数为0，每迭代一次就选择一条满足条件的最小代价边，加入到最小生成树的边集合里。

实现思想：以最低代价加入边。 用一个表： （weight（边权），Vertex1（点1），Vertex2（点2）） 用并查集检查下一个边的两个点是否已连接。

判断两个点是否已连接需要$$O(log_2|E|)$$，工执行e轮。 则时间复杂度=$$O(|E|log_2|E|)$$，适合边稀疏图